W循环多重网格的图像立体匹配优化算法*
2020-12-01卢冬山刘宝龙
郭 怡,卢冬山,刘宝龙
(1.西安工业大学 信息技术中心,西安 710021;2.西安工业大学 计算机科学与工程学院,西安 710021)
双目视觉是模仿人类视觉原理来建立物体的三维立体信息,尤其是深度信息,在工业测量、医疗和无人驾驶等领域有着广泛的应用[1-3]。
立体匹配是双目视觉下三维重建的关键步骤,其目标是寻找空间点在双目相机中左右成像点之间的对应关系,并由此产生评价匹配效果的视差图。依据是否存在全局能量函数将立体匹配算法分为两种:局部立体匹配算法和全局立体匹配算法[4-5]。
局部匹配算法主要是采用局部优化方法进行视差值估计,先以待匹配左图中某个像素点为中心建立一个匹配支撑窗口,且用此窗口内的灰度分布来表示此像素点,在待匹配右图中寻找与其相对应的像素点,通过同样的方法,以对应的像素点为中心建立规格相同的支撑窗口,使得窗口内灰度值分布与左图之间满足一定的相关性限制条件。相比全局匹配算法中的能量函数,局部算法没有平滑项约束,效率相对较高,但匹配的正确率较低[6]。
全局匹配算法通常不使用窗口相似度来获得视差值,而是使用全局优化观念,建立全局能量函数,此函数中包括数据项与平滑项,全局能量函数取最小值时所对应的视差是最匹配的。全局算法相较局部算法精度高,但求解过程复杂且时间复杂度高[5]。
常见的全局立体匹配方法有动态规划算法、置信传播算法、模拟退火法和基于图割的算法等[7]。它们都是构建包含数据项以及平滑项的能量函数,然后对能量函数进行最小化来求取最终的视差值。
动态规划算法实质上就是将多阶段过程的大问题转化为多个小问题,并把这些小问题进行逐个求解,最后将这些最优解组合起来解决最佳匹配点的问题。一般小问题的划分是依据时间或空间来进行划分的。传统的规划算法是以极线约束为基础的,在极线约束的范围内用此方法在左右图像中同一扫描线上进行对应点的匹配,使用动态择优的路径规划构造最小化能量函数,得到匹配之后的视差图。这种方法需要对图像进行行扫描,结果会使得生成的视差图上出现条纹[8]。
置信传播算法是一种通过概率函数来定义的匹配方法。它是由马尔科夫场(其中的节点只和相邻节点间存在关系)模型来描述的,其中网络传输节点用像素点表示,节点中包括信息消息和数据消息,存储对应像素的视差值和节点的匹配消息值。置信传播算法将图像中的像素点在四面相邻的像素网格上进行编号,然后对已经编号的像素点进行搜索匹配,匹配消息对于无纹理的图像区域具有很强的适应性,大大提高了立体匹配的精度,但是存在单个像素点之间易发生误匹配的情况,而且要对全局图像展开搜索,会导致时间复杂度增大[5]。
基于图像分割的立体匹配算法是一种能量优化算法,此算法首先建立赋值权重图,赋值权重图是依照能量函数中每个因子来定义的,为马尔科夫随机场中的赋值权重图及其配置形成相应的约束规则,最后通过赋值权重图最小分割来对目标能量函数极小化,即对全局能量函数求最小化转化为赋值权重图中的最小分割求解问题,一般使用最大流算法求解,此方法可以很好地改善并解决动态规划匹配算法中的条纹缺陷,但是其时间复杂度较高[7]。
基于动态规划的立体匹配算法运行效率较高,但是匹配精度不高,容易得到条纹图像,而基于图像分割方法的立体匹配算法则能解决动态规划中求出的条纹缺陷,而且图像边缘匹配效果好,但是算法运行效率不高;基于置信度传播的立体匹配算法求解的收敛性相对较差,运行效率也不高,但是对于低纹理方面的图像具有很好的鲁棒性[5,8]。
综上所述,没有一种匹配算法具有普遍适用性,需要根据不同的场合及实验需求来选择合适的立体匹配算法,然后达到想要的效果。传统区域的立体匹配方法都是基于灰度特性的,尤其对于纹理少、光照不均匀等情况则难以找到正确的对应点。本文采用一种基于多重网格的变分方法,此方法是一种全局匹配方法,它实质就是寻找一个能量匹配函数,并对其最小化来求取像素点之间的视差值。利用约束准则及最优化理论对方程进行求解。其中定义的能量函数不仅与像素点灰度值相关,还和梯度值和视差间的平滑性有关,有效的预防了匹配时对像素间灰度值的依赖,利用W型循环多重网格进行迭代求解,求出最优解,使所得的视差图平滑且密集。
1 多重网格基本思想
多重网格算法是使用粗细不同的多等级网格来“修正”细网格下误差的方法,它加快了方程组迭代求解的收敛速度。相比其他的迭代方法具备收敛速度较快,精度更高和时间复杂度低等优点[9]。
假使要迭代求值的一系列问题为Lμ=f,当中的L可以是微分、积分或者是利用泛函数求极值的算子。最初的迭代求解是在固定的网格上新建差分方程,根据差分方程变换出一组线性或者非线性方程组,最后采用特定的迭代方法,比如高斯-赛德尔迭代法、牛顿迭代法、超松弛迭代法以及在它们基础上改进的迭代方法等。而多重网格算法并不是在固定的一层网格上迭代求解,而是通过不同粗细的网格进行方程的迭代与修正求解。
若存在一组网格Ω0,Ω1,…,ΩM,这组网格被称作网格序列Ωk(k=0,1,…,M)。在k递增的过程中,差分网格会变得更细,而且这些网格都用相同方式进行细分,然后无限接近于区域Ω。
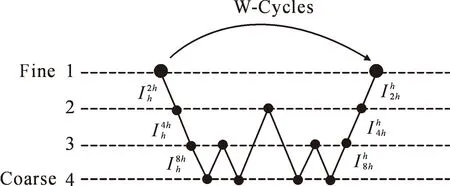
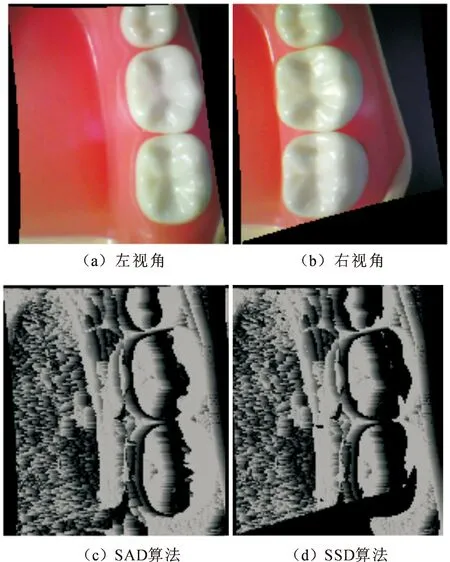
多重网格的实质是在粗网格Ωk(k 细网格上的离散微分方程为 Lhμh=fh,Ωh∈G(Ωh)。 (1) 式中:Ωh为在细网格上求解;G(Ωh)为细网格Ωh所处的函数取值空间。其中基于粗网格的微分方程为 LHμH=fH,ΩH∈G(ΩH)。 (2) (3) 通常取值为 2) 粗网格到细网格校正操作步骤为 双网格法如图1所示。 图1 双网格方法Fig.1 Method of double grid 多重网格方法实质上是在多个级别的网格上进行反复的迭代和修正,即在粗细不同的网格间多重使用双网格法,但是仅在最粗网格上精确求解线性方程。在数次迭代过程下,可知低频分量减少的较为缓慢,而高频分量减少的稍快。在最粗的网格上,方程中存在较少的未知量,因此运算量相对细网格少,但是求解的精度稍低。因为粗网上的高频分量不显示,而低频分量容易显现,所以充分利用细网上的松弛操作和粗网上插值校正操作,这样可以让高频分量和低频分量得到充分减少,由此可保证算法的收敛性[9]。 基于多重网格的变分立体匹配方法中,将能量值分配给每个可能的视差字段[10-11],具有较低能量的视差场优于具有较高能量的视差场,计算出具有最小能量的视差场并返回。其中,能量函数包含数据项和平滑项,数据项表示对应点是成像场景中的相同部分,所以具有相等灰度值,反映的是像素在不考虑邻近像素的情况下自身的倾向。平滑项表示成像场景及其视差场是分段平滑,表示的是相邻像素之间在视差上的相互影响,这将对数据项中低纹理的区域进行视差插值,例如没有纹理的区域。 针对匹配代价函数作如下假设: 1) 关于灰度值的恒定性,假设对应点具有相同的灰度值,即 I1(x,y)=I2(x+u(x,y),y)。 (4) 2) 关于灰度值梯度的恒定性,假设对应点具有相同的灰度值梯度,即 (5) 上式假设的梯度值差异是通过左右图像上像素点的梯度差的L2范数建立的,灰度值梯度不受添加光照条件变化的影响。 4) 视差场的平滑度:假设得到的视差场是分段平滑的,由视差场的导数的L2范数建立,平滑约束表示相邻像素间具有相等或接近相等的视差值。 5) 平滑项中的统计鲁棒性:类似于数据项,为了减少异常值的影响,在平滑项上应用了全变分。有利于保留视差场中的物体边缘信息。 能量函数是上述项线性组合的积分,能量函数中使用符号含义见表1。 表1 能量函数符号说明Tab.1 Description of energy function symbols 能量函数为 E=Edata+Esmooth- Smoothness·Ψ(|u(x,y)|2)dxdy。 (6) 式中:Edata为数据项,表示在给定视差下,左右图像像素灰度不一致性的程度,Esmooth为平滑项,表示给定视差下局部的平滑程度。 W型多重网格迭代方法包含三部分:细网格松弛步骤、粗网格插值校正步骤和反复迭代过程,细网格松弛步骤用来校正粗网格求解所带来的误差,粗网格插值校正步骤用来解决细网格求解所带来的误差,反复迭代过程利用残差量对上下各层网格间反复迭代求取最优的解。也就是说通过一个W形迭代过程来对初始值不断的进行求解修正,得到最终解。其中,利用两级W循环的多重网格求解示意图如图2所示。 图2 W循环多重网格示意Fig.2 W-Cycles grid 图2中,粗网格下的迭代由大黑圆点表示,而小黑原点表示求精确解的迭代。在校正周期上,进行预松弛步骤,再迭代执行一定次数。接着进行粗网格校正步骤,最终进行后松弛步骤,得到准确的解。 W循环多重网格算法过程为 在第一层网格Ωh(即初始最细网格)上的方程 Ahuh=fh。 (7) 式中:h为细网格的步长;Ah为细网格Ωh下的微分算子;uh为此方程的解,即最后迭代要求的精确解;fh为多重网格法使用时引入的数值源项。假设vh是Ωh上的近似解;定义下一级网格步长为上一级步长的2倍,即H=2nh,(n=1,2,…,n),且A2nh是离散化的微分算子,u2nh为下一级粗网格中求得的方程的解,则下一级粗网格上有线性方程为 Ahuh=fh。 (8) 假设连接上下两层网格的限制算子和插值算子表达式为 (9) 式(8)和式(9)实际上是不同形式下的相同方程,由粗细不同的四层网格上组成的W循环多重网格步骤如下: 1) 设vh0是初始值,在第一层网格Ωh(即最细网格)上对方程Ahuh=fh进行迭代运算得其近似解vh和残差rh=fh-Ahvh; 在立体匹配前先进行极线校正,使得左右相机处于水平一致的情况下。为了验证本文算法的视差图效果,将灰度差的绝对值之和 (Sum of Absolute Value of Gray Differences,SAD),灰度差的平方和(Sum of Squared Value of Gray Differences,SSD),与基于W型的多重网格算法进行比较分析。 利用一组左右匹配图及其真实的视差图来测试局部窗口匹配算法和本文提出的基于W循环的多重网格匹配算法。匹配测试用图来自Middlebury标准库,如图3所示。 本文窗口匹配SAD、SSD算法参数设置如下:最大视差设置为30,匹配的窗口分别为3*3,7*7,9*9,11*11,具体视差效果见表2。从表2可看出,当匹配窗口逐渐增大时,视差图中物体的边缘细节会更加的模糊,很明显,3*3的窗口比17*17的窗口拥有更加清晰的物体轮廓,但是更容易出现视差不连续的情况。从图3可看出,局部窗口匹配算法对于形状简单的图形可实现较好的匹配,如图3中那个面具,得到的面具轮廓比左边的圆锥体轮廓更为清晰,但是局部窗口匹配得到的视差图不够平滑。 通过本文提出的基于W循环多重网格匹配算法得到的视差图如图4所示,相比局部窗口得到的视差图从视觉上更加平滑。 图4 W型循环多重网格视差图Fig.4 Disparity map for W-Cycles grid 为了对匹配效果进行定量分析,参考以下两个评价参数: 1) 平方根误差,匹配实验得到的视差图和真实视差图间的平方根误差为 (10) 式中:N为图像中像素总数;dc(x,y)为匹配之后得到的视差图里坐标(x,y)所对应的像素值;dr(x,y)是真实视差图里(x,y)所对应的像素值。 2) 整体误差,图像中所有像素的误差为 (11) 其中δd表示可接受的误差。 三种不同方法的定量比较见表3。从表3中可以看出,本文所提算法较好的降低了匹配误差,整体误差降低了约20%。 表3 视差图出错对比表Tab.3 Comparison of disparity map’s errors 针对上述分析,为了检验纹理信息不明显的匹配对象,本文选取一组牙齿照片进行测试,选取N=3的局部窗口匹配和本文算法进行比较,其中窗口匹配如图5所示。 图5 窗口匹配效果(N=3)Fig.5 Results of window matching 图5可看出,牙齿表面具有纹理少、光照不均匀等特征,而局部立体匹配中,是以灰度值为特征来进行匹配的,针对图像中稀疏纹理区域,通过改变局部匹配窗口的大小(如3*3和11*11)都很难得到较为平滑的视差图,且在同一深度区域匹配的像素点错误较多。 图6是基于多重网格的变分方法得到的视差图,一般来说,离双目视觉系越近,视差图的颜色越深。为了降低灰度值对匹配的影响,此时设置灰度值权重为0.18,梯度值权重为30,平滑项权重设置为5。并通过两层W循环来对匹配代价函数进行迭代求取视差图。 图6 视差图Fig.6 The final disparity map 由于减少了对于灰度值匹配的依赖,基于多重网格的变分方法可以在视差图中更清楚的展示牙齿的表面轮廓,并且得到的视差图较为平滑。 为了判断每个像素的视差质量,计算从第二幅图像到第一幅图像的反向视差图并将其与图6的视差图进行比较,以Score为单位返回,Score为图像灰度值,其中像素值范围为0~10,其中0为最佳质量,10为最糟糕的。即越黑的地方匹配的准确率越高,其视差分数如图7所示。实验结果表明,本文所提算法对纹理特征少、光照不均匀的匹配对象也能有效提高匹配效果。 图7 视差分数图Fig.7 Parallax fractional map 本文采用一种基于多重网格的变分方法,利用约束准则及最优化理论对方程进行求解。利用W型循环多重网格进行迭代求得最优解,使得双目视觉的视差图平滑且密集,有效降低了立体匹配误差。多重网格算法使用粗细不同的多等级网格来修正细网格下误差的方法,加快了方程组迭代求解的收敛速度。相比其他的迭代方法具备收敛速度较快,精度更高和时间复杂度低等优点。针对窄基线下纹理特征不明显的重建表面,该方法鲁棒性较强,可以得到更为平滑准确的视差图。
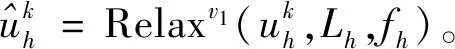
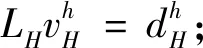

2 匹配代价函数的构造
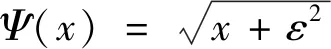


3 匹配代价函数的优化

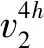

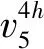
4 立体匹配实验及结果分析




5 结 论
