基于浸没边界法的流固耦合模拟分析
2020-11-30秦如冰
秦如冰,柴 翔,程 旭
(上海交通大学核科学与工程学院,上海 200240)
第四代快堆系统设计过程中关注的是固有安全性以及被动安全性。反应堆的固有安全性表示设计应使其仅依据自然状态即可保持安全状态;并确保所有可能的情况下所有性能特征都处于安全范围内。被动安全性有更加广泛的定义,表示无需任何人为干预,不用触动信号,也不需要实现外部供能,反应堆就可以保持安全状态。非能动停堆组件体现的正是这样的特性。钠冷快堆(Sodium-cooled Fast Reactor,SFR)作为第四代反应堆系统的重要堆型之一,采用非能动停堆组件以保证其安全性已成为国际上快堆发展和研究的最主要研究方向之一[1]。
然而,在对非能动停堆组件落棒停堆过程进行模拟分析时。由于复杂几何、存在孔隙结构以及运动边界等问题的存在,传统计算流体力学程序(Computational fluid dynamics,CFD)所使用的结构化网格或非结构化网格生成方法存在较大的局限性。浸没边界法(Immersed boundary method,IBM)是CFD中的一种方法,该法无需构建贴体网格,而是采用笛卡尔网格,并通过添加体积力将边界条件纳入控制方程中,简单的网格和数据结构非常适合处理复杂几何和移动边界问题[2]。IBM最早于20世纪70年代由Peskin[3]提出,它最初用于模拟心脏中的血液流动模式;经过多年发展已广泛应用于工程模拟中。
本文针对钠冷快堆非能动停堆组件落棒过程模拟困难的问题,基于浸没边界法的特性,开发适用于复杂几何和移动边界问题的数值模拟程序,并对程序进行验证分析。本文验证了层流状态不同雷诺数的二维(2D)工况,包含固定和振荡圆柱绕流的模拟结果。本文工作为后续三维工况、湍流以及实际几何模型的模拟分析验证提供了坚实的基础。
1 数学模型
1.1 网格类型
程序中涉及两种网格。第一种称为背景网格,为包含整个计算域并忽略浸没体的笛卡尔网格。第二种网格用来表示浸没体的几何表面[4]。该表面网格无孔,因此可将浸没体内部与流体完全分离。
将表面网格嵌入背景网格中会把背景网格划分为三种不同类型。欧拉网格(或流体网格)是指完全在流体区域中的网格,拉格朗日网格(或固体网格)则完全在浸没体内,浸没边界网格(IB网格)与浸没体表面网格相交。表面网格上的节点称为浸没边界节点(IB节点)如图1所示。在背景网格的欧拉场的流体网格中求解流动的控制方程,并且通过浸没体的拉格朗日网格来跟踪表面的位置和形状。通过在背景网格中重新定位浸没体可以解决边界的运动问题,并通过重新生成表面网格可以解决浸没体表面可能产生的变形。

图1 浸没边界法网格划分示意图Fig.1 Cell types in IBM
1.2 程序求解过程
预估步:
不含重力的不可压缩流体Navier-Stokes公式为 :

(1)
连续性方程如下所示:
·U=0
(2)
使用公式(1)求解不包含浸没边界(IB boundary)区域的预估速度u*。在求解矢量时,公式(1)变为:
Au*=r′u-p
(3)
式中:A——系数数组乘以解,u*;
r'——系数数组乘以上一步的速度u。
u*是唯一的未知数。可将A的系数数组分为对角矩阵和非对角矩阵,向量形式化为:
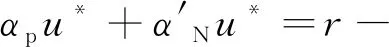
(4)
式中:αp——A的对角矩阵;
α'N——A的非对角矩阵;
r——r'·u*的矩阵。
公式(4)可以化为:

(5)
式中:αN=r-α'Nu*。
校正步:
包含校正步速度贡献(不含压力)的变量U可通过下式计算得到:
(6)
IB网格上的速度通过公式(7)进行插值处理可得:
(7)
式中:x,y——网格坐标;
C——插值系数;
下标p——IB网格;
下标ib——IB节点的参数。
进而公式(5)可化为:

(8)
考虑到连续性方程,公式(8)可变为泊松方程以求解修正压力:

(9)
IB网格和流体网格界面的通量可通过公式(10)计算得到:
(10)
式中:fib——IB网格和流体网格的界面;
f——靠近IB的流体网格界面;
S——界面面积;
n——界面法向量;
v——界面上的法向速度。
由公式(11)给出计算:
(11)
通过以下公式计算不包括压力作用的通量:
(12)
根据公式(9)得到的修正压力,通量可修正为:
(13)
同样的,用修正压力来修正速度,通过将公式(6)与压力梯度相加可得更新后的速度为:

(14)
在程序实际求解过程中,插值方程系数C通过建立未知系数求解矩阵得到:
C=(MTWM)(-1)MTWA
(15)
A为由ui-uP作为元素构成的矢量,矩阵M表示处理狄利克雷边界条件时扩展模板网格的几何位置信息,对于二维工况令Xi=xi-xib,Yi=Yi-Yib,则有:
(16)
对于固定浸没体,包含几何位置信息的M矩阵只需计算一次,对于运动物体即移动边界问题则需要在每个时间步上重新进行计算。W则为由权重wi作为对角元素的矩阵,权重与插值网格与浸没边界网格的距离成反比。
对于诺依曼边界条件,反应插值模板几何位置信息的矩阵M则应写为:
(17)
与狄利克雷边界条件类似,诺依曼边界条件下矢量A包含了插值模板的压力值以及压力梯度,即:
(18)
由于边界条件是通过插值计算来施加的,因此浸没边界网格中速度值的增大或者减小将违反计算域流体的质量守恒条件。因为浸没边界网格界面上的速度是通过浸没边界网格和相邻网格线性插值得到的,当计算通过浸没边界网格界面的流量时,这一影响将变得更加明显。为了纠正此不足,需要在浸没边界网格界面上应用适当的缩放因子进行流量调整。流量不平衡的情况通量通过流动比率进行衡量,由下式表示流量不平衡情况:
Fimb=Fin-Fout-Fib
(19)
式中:Fin和Fout分别代表流体流入以及流出与浸没边界网格相邻的流体网格。Fib是由于浸没体边界移动(Sib)所产生的流体流动速率,并由下式定义:
(20)
由该项衡量弹性所产生的影响,对于刚体而言,根据高斯散度定理,该项为零。如果不平衡项Fimb不为零,则通过调整并缩小Fin和Fout中较大的值来进行修正。调整方式为乘以小于1的调整因子,调整因子的大小根据Fin和Fout的比值确定。
2 程序验证分析
为验证本文开发程序正确与否,构建以下几何模型用于验证分析。流体流经直径为D的二维(2D)圆柱,如图2所示,计算域是高度为H,长度为Li+L0的长方形。入口处的边界条件为沿着流动方向x施加稳定的均匀速度以及零压力梯度。在出口处则采取质量守恒条件和零压力梯度。计算域的顶部和底部采用速度的自由流边界条件。

图2 计算域及边界条件Fig.2 Computational domain and boundary conditions
将圆柱的中心点定义为原点,计算域的尺寸遵循如下准则,在x,y方向上满足[-16D,48D]×[-16D,16D]的几何尺寸[5]。并将计算域的网格分不同区域进行细化,细化区域及细化网格尺寸如图3所示,网格在圆柱的周围是均匀的,对应区域范围为-D≤x≤D,-D≤y≤D。根据以上原则,在程序中生成用于模拟计算的网格如图4所示,为节省计算资源,在模拟固定圆柱工况时圆柱内部的背景网格因不参与计算不需要进行加密。通过图4圆柱所在位置我们可以看出程序计算时无需生成贴体网格。

图3 计算域划分及网格尺寸Fig.3 Computational domain decomposition and grid spacings

图4 程序计算所生成的网格Fig.4 Mesh in the code
程序验证是基于流体流经直径为D的固定或振荡圆柱的二维(2D)模拟,并在各种雷诺数(Re=U∞D/μ)下进行的,并将计算结果与文献中的数据进行对比。斯特劳哈尔数(St),阻力(CD)和升力(CL)系数由式(21)定义,其中fv表示脱落频率,Fd和Fl分别表示单位长度的阻力和升力。各种算例验证过程中所涉及的几何模型、雷诺数以及所需比较的参数如表1所示。
(21)
式中:L——再循环长度;
a——圆柱与再循环中心之间的距离;
b——两个再循环中心的垂直距离;
θ——后驻点的分离角。
稳态流动下的涡旋特征参数如图5所示。

表1 程序验证分析工况汇总

图5 涡旋特征参数Fig.5 Characteristic geometrical parameters in the steady regime
Re=30时的流动为稳态,特征在于位于圆柱后稳定的再循环区域。圆柱体周围的网格尺寸为Δx=Δy=0.01D,经过模拟后得到的数据,图5中定义的所有特征几何参数与表2中的文献数据相当,经细化网格后模拟的结果误差小于10%。

表2 Re=30时模拟结果与文献对比
随着雷诺数的增大,根据Williamson[9]和Norberg[10]的研究,Rec=40为流动转为不稳定流动的临界值,因此,模拟了在Re=100和185时的工况,即具有涡旋脱落的2D非稳态区域模拟,圆柱体周围的网格尺寸为Δx=Δy=0.01D,图6展示的涡旋轮廓为著名的卡门涡街,其特征在于涡旋的周期性脱落,对流并从圆柱体上向后散开,将Re=185时的涡脱落结构与Guilmineau[12]和Pinelli[5]的工作进行对比,结果符合较好。

图6 Re=185时的涡脱落Fig.6 Vorticity countours at Re=185
CD和CL随时间t的变化,其中时间做无量纲处理作为自变量,如图7所示,表明升力和阻力波动的幅度随着雷诺数的增加而增加,符合Guilmineau和Queutey[12]的研究结论。
对于不稳定流动两个不同雷诺数下得到的模拟数据:斯特劳哈尔数,平均阻力(在10个时间段内计算)和均方根升力系数与表3和表4中总结的文献数据相当。

表3 Re=100时模拟结果与文献对比Table 3 2D flow past a fixed cylinder at Re=100. Numerical and experimental data from the literature are provided for comparison

表4 Re=185时模拟结果与文献对比 Table 4 2D flow past a fixed cylinder at Re=185. Numerical and experimental data from the literature are provided for comparison

图7 CD和CL随时间变化图Fig.7 Temporal evolutions of CD and CL for the 2D flow at Re=100 (a);Re=185 (b)
针对Re=185时做网格敏感性分析,得到阻力系数在不同网格尺寸下的变化情况。在上述模拟分析验证过程中,共进行了5次加密,笛卡尔网格的最小尺寸为Δx=Δy=0.01D。为了进行网格无关性验证,本文分别计算了加密次数为1至4次时的阻力系数与升力系数变化情况,对应的笛卡尔网格最小尺寸分别为:Δx=Δy=0.16D、0.08D、0.04D、0.02D。不同网格尺寸下得到的阻力系数随时间变化如图8所示,可以看出,当最小网格尺寸为0.02D时与0.01D下的计算结果相近。
在Δx=Δy=0.01D以及0.02D下分别对阻力系数曲线做快速傅里叶变换,阻力系数的频谱分析图9如所示,当网格最小尺寸为0.01D时,频率等于0时振幅最大为1.28,当网格最小尺寸为0.02D时,频率等于0时振幅最大为1.29。由此可知当网格尺寸小于0.02D时即可满足网格无关性要求。

图8 不同网格尺寸下,阻力系数CD随时间的变化Fig.8 Drag coefficient CD as a function of the time for the 2D flow past an oscillating cylinder at different cell size

图9 阻力系数频谱分析图Fig.9 Frequency-amplitude plot of drag coefficients
为了验证程序处理移动物体的能力,在Re=500下,对流体流经正弦运动的圆柱体工况进行了二维模拟。圆柱体在垂直方向上以固定的振幅比A(=ymax/D)=0.25以及频率比F=f0/fv=0.975(f0为圆柱振荡频率)。计算域与计算固定圆柱体时模拟的域相同,圆柱体周围的网格尺寸为Δx=Δy=0.02D。脱落频率fv为Re=500时,基于二维固定圆柱绕流的模拟结果。一旦流动稳定为2D涡脱落状态,我们便开始移动圆柱体。
在图10中详细描述了圆柱做正弦振荡的流程。 左边的五张图显示了在整个涡旋脱落周期一半的过程中五个瞬间绘制的涡旋轮廓,在此期间,升力沿向上的方向起作用。与右边所示的Blackburn[6]的模拟结果进行比较,对比结果显示计算较为准确,进而可以很好地预测涡脱落过程的空间动态以及附着点和分离点随着时间的演变。图11显示了在最后10个振荡周期内取升力系数的平均值随时间的变化,其中时间做无量纲化处理2πt/T,T为圆柱振荡周期。同样,结果可以认为与Blackburn[6]的参考数据非常匹配。

图10 在Re=500时,二维振荡圆柱绕流的瞬时涡轮廓Fig.10 Instantaneous contours of vorticity for the 2D flow past an oscillating cylinder at Re=500
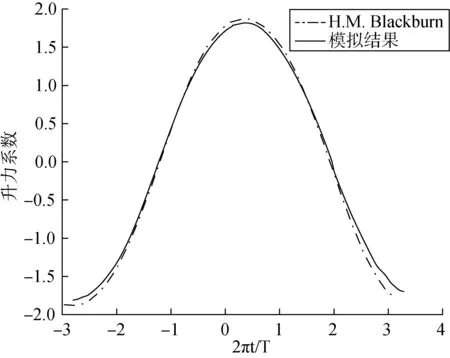
图11 在Re=500时,升力系数CL随时间的变化Fig.11 Lift coefficient CLas a function of the time for the 2D flow past an oscillating cylinder at Re=500
3 结论
本研究开发了基于浸没边界法的CFD程序求解器。对移动和固定的二维圆柱绕流工况在不同雷诺数下进行模拟验证分析,雷诺数变化范围为30到500,包括稳态流动和不稳定流动共4种不同工况。将计算所得的特征几何参数、阻力系数、升力系数以及涡脱落情况等参数与文献进行对比,模拟结果显示,使用本程序计算具有良好的效率和准确性。并针对Re=185的工况进行网格敏感性分析,通过阻力系数完成了网格无关性验证。但目前的模拟范围还只限于2D工况以及雷诺数较小的层流,本文为未来工作聚焦于验证3D以及湍流下模拟结果的准确性,并针对钠冷快堆非能动停堆组件停堆落棒实际情况中面临的核反应堆热工水力复杂几何问题进行模拟打下了基础。
