一种简单判定二次应力的方法

兰天宝，田金梅，周 航，王艳苹

(中国核电工程有限公司，北京 100840)

根据压力容器的失效形式和危害性，规范ASME Ⅲ、RCC-M等将应力进行了分类，分为一次应力、二次应力和峰值应力，各应力对结构破坏危害程度是不同的，因此，规范中对不同应力规定了不同的许用极限。设计者需要依据规范对各种类的应力分别评定，保证其满足规范要求。一次应力是为平衡压力与其他机械载荷所需要的应力，又称为载荷控制应力和平衡控制应力，它是维持结构各部分平衡所必需的，其基本性质是没有自限性。当一次应力超过材料屈服极限将导致设备失效，引起总体变形，因此一次应力的危害很大。(一次应力又细分为一次总体薄膜应力，一次弯曲应力和一次局部薄膜应力)。二次应力是为满足外部约束条件或结构自身变形连续要求所必需的应力。二次应力不是为满足平衡外载荷所必须的，是由于变形协调的需要而产生的一个自平衡力系，其主要特征是具有自限性，即当二次应力超过极限值时，只发生少量的局部塑性变形就能满足结构的连续性条件，塑性流动就会停止。只要不反复加载，结构就不会破坏，因而其危害较小。

由于有限元计算方法的广泛应用，在解决实际工程问题时，计算者需要对有限元应力结果进行应力分类，以便对不同应力按照规范要求进行评定。由于规范中对一次应力和二次应力有不同的限制准则，如将二次应力归入一次应力进行评定会导致设计过于保守，而将一次应力误划入二次应力会导致危险的设计。因此，在难以根据定义进行有限元应力结果提取分类时，提出一种既准确又简单的判定二次应力的方法是工程实践迫切需要的。

1 应力分类主要方法

尽管各种压力容器设计规范标准中规定了应力分类的方法和规则，但将应力分类方法应用到工程实践时却存在很大困难。一直以来，研究人员不断完善规范中的相关内容，致力于提出更为方便实用的应力分类实现方法，下面主要介绍一些最为常见的应力分类方法。

1.1 规范定义法

规范定义法是最为简单常用的方法，需要设计人员依据对规范的理解及经验来区分一次和二次应力，对于简单结构来说依据规范便可判定二次应力。RCC-M在C篇表C3382给出了几种典型情况下的容器应力分类[1]。表1列出了规范中部分结构应力分类。

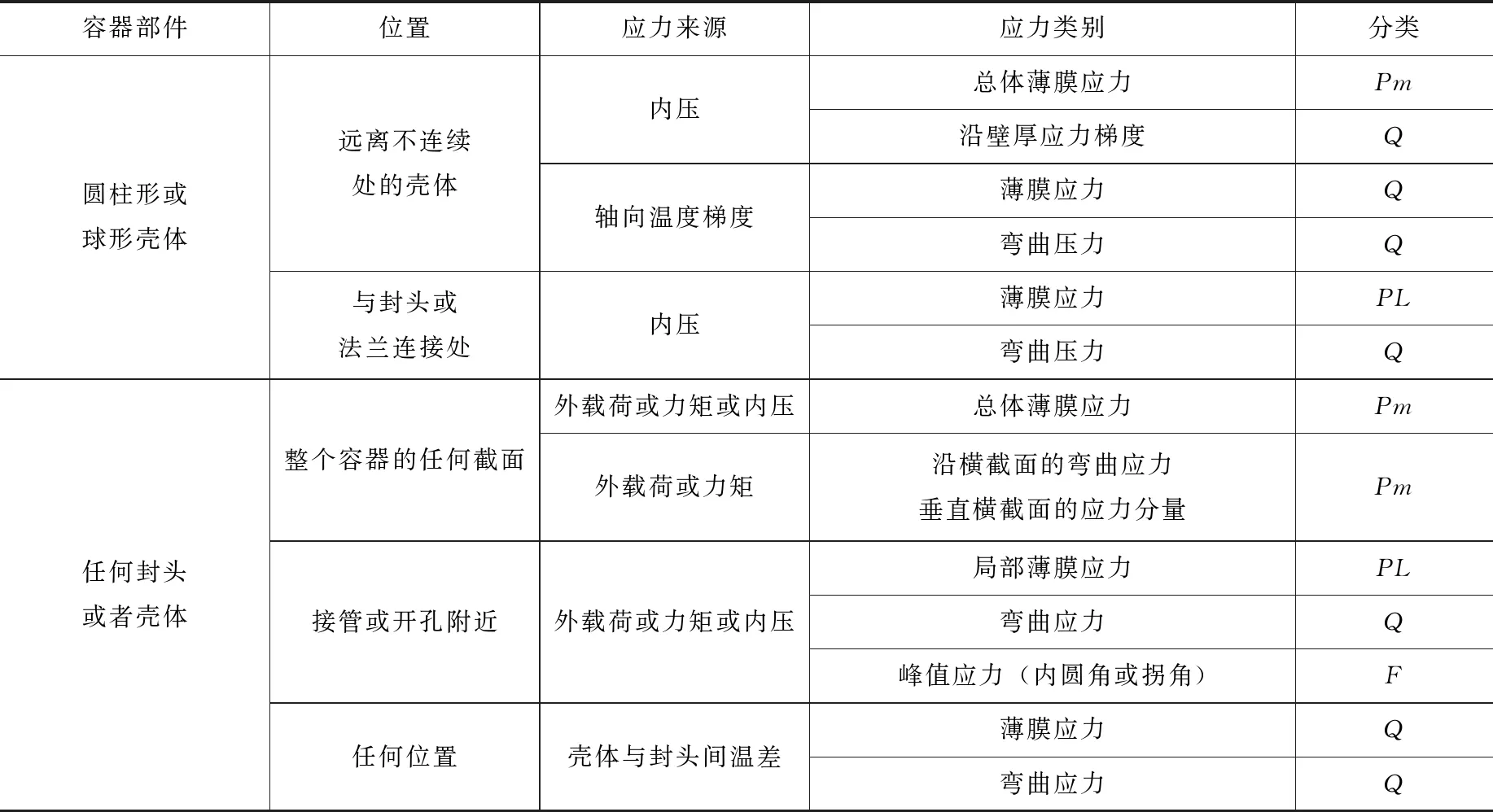
表1 容器应力分类

对于简单的结构，如封头连接区域依据规范很容易判定二次应力部位，但对于复杂连接区域或构件，仍然无法依据规范明确地判断二次应力。

1.2 一次结构法

在总体结构不连续处会产生局部薄膜应力，局部薄膜应力具有一次特性与二次特性，为了安全起见，通常都按一次应力考虑，但这样处理会导致设计上的过于保守。不同部位的局部薄膜应力的区域范围不同，应力重分布特性不同，因此为减少设计的保守性，可将总体结构不连续引起的较高的弯曲应力归入二次应力。

为此，陆明万等提出了一种有效的应力分解法，即一次结构法[2]：一次结构法的实质是构建组成容器的各元件在机械载荷(如压力、地震、重力载荷等)作用下的一次计算模型，以期先行解决各元件的一次应力强度问题，这样不必考虑各元件由于变形协调引起的相互作用力产生的二次应力，为此称为一次结构。以平盖和筒体连接处为例，如图1所示。将平盖与筒体连接处的弯曲应力归为二次应力，解除B处对转角的连续性要求，只保留位移的连续性，取薄膜应力状态下的筒体和平盖作为一次结构。得到的一次结构，便可按照静力强度分析计算。

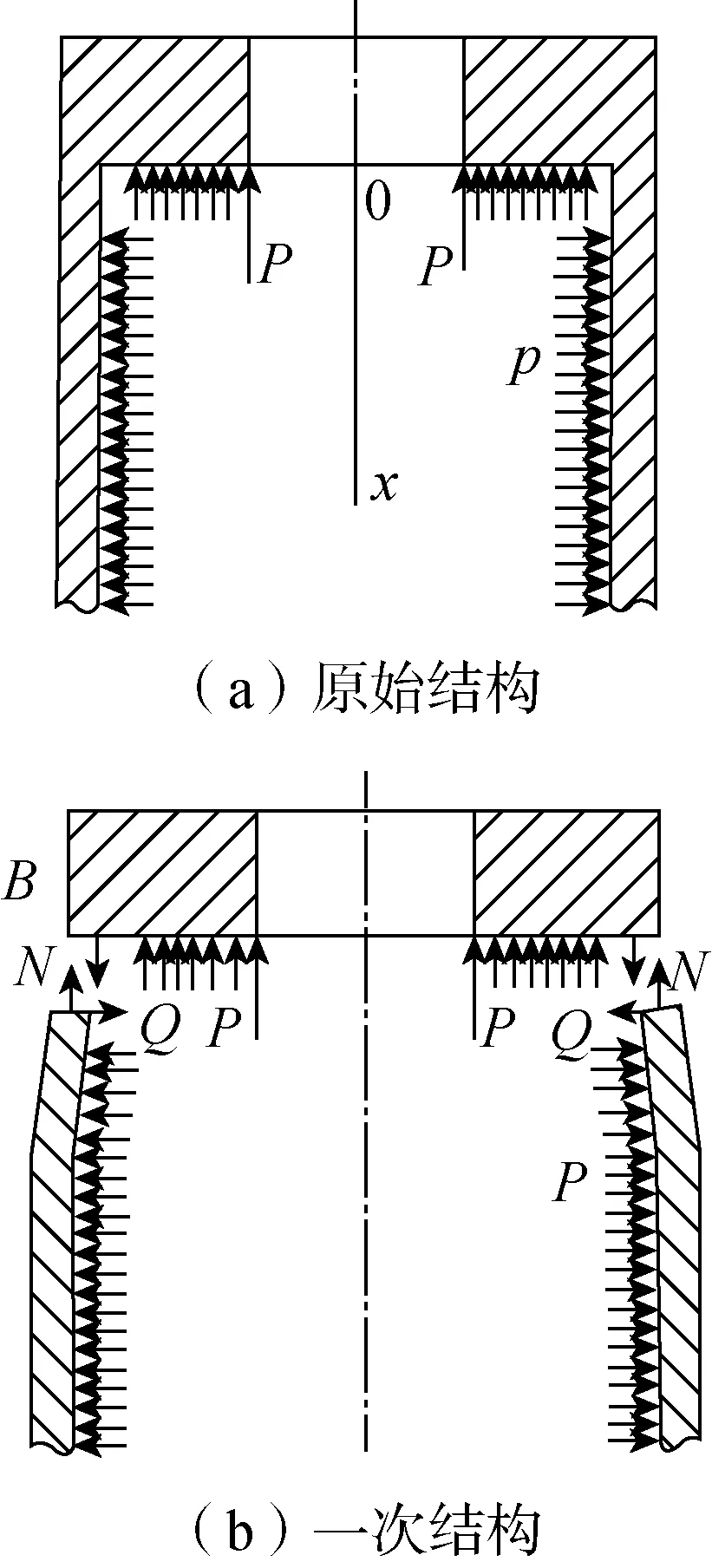
图1 开孔平盖的原始结构与一次结构Fig.1 Original and primary structure of open flat cover

但对于具体工程问题，对于复杂结构和模型，将结构分解为一次结构十分不便。

1.3 弹性补偿法

Dhalla的研究提供了分解一次应力和二次应力的方法和步骤，如图2所示。首先进行一次弹性有限元计算，使其产生超过屈服极限的应力，用线O-A表示。然后考虑塑性影响，修改应力超过屈服极限的单元的弹性模型，使用新的弹性模量再次进行分析计算，得到线O-D，如果将O-D延长到B点，与最初的A点相比应力的增加为一次应力，线A-B称为100%一次应力线。相反如果线O-D达到C点，一次应力的成分逐渐减小，在C点达到零，直线A-C为二次应力线。因此一次应力的比例和夹角θ有关。

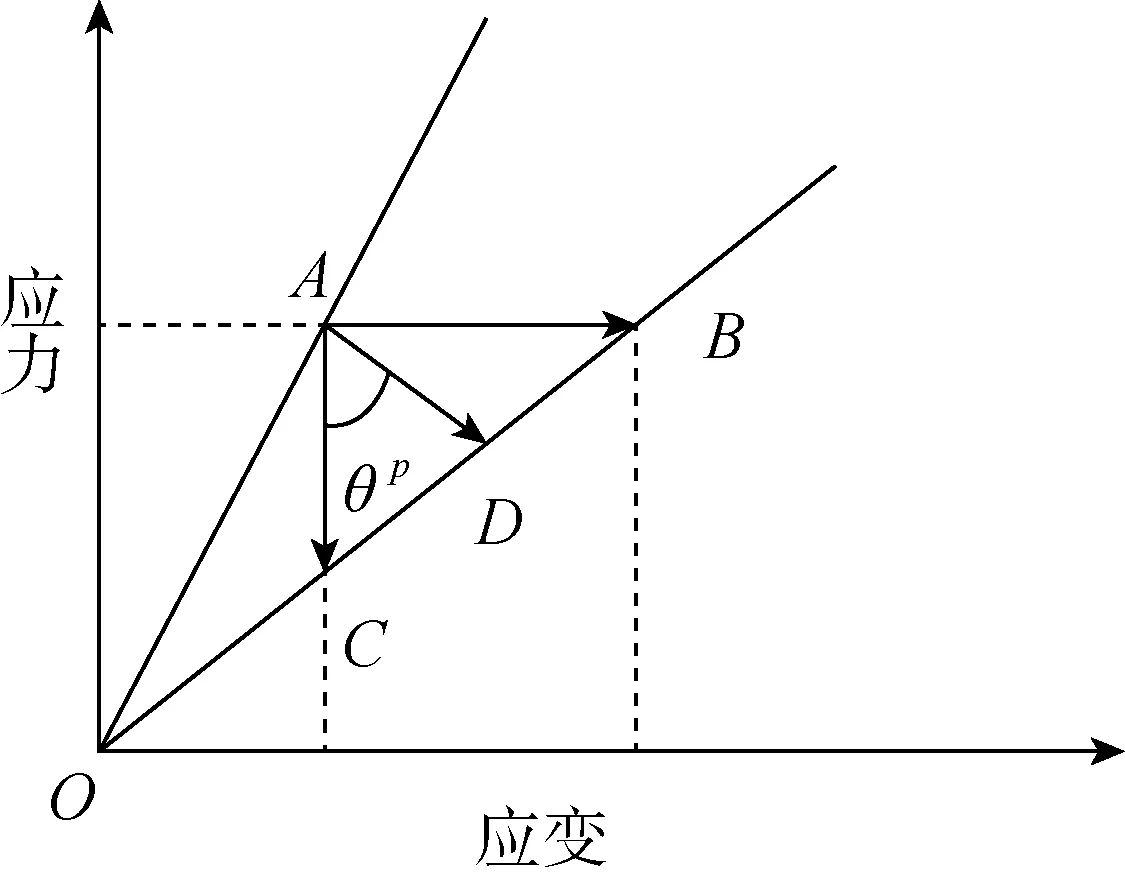
图2 理想情况下的应力-应变响应曲线Fig.2 Ideal stress-strain response curve

具体的实践细节，本文不再赘述，可以参考Dhalla的相关研究文章[3]，但是通过上述介绍可以看出该方法应用十分繁琐，因此未在工程实际中得到广泛应用。

2 简易判断二次应力法

目前有限元方法仍是解决大多数复杂结构工程问题的好方法，因此，基于有限元操作分析，本文提出简易判定二次应力方法。即若由集中力、压力和自重等载荷导致的应力与结构的弹性模量无关，则结构的弹性模量只影响结构的变形而对应力无影响。

二次应力的产生是基于结构直接的互相约束、协调变形，因此基于协调变形关系求解出的应力是与结构的弹性模量有关的。这是由于应力由构件自约束产生，而不是由平衡外载产生，这种由于各部分变形协调产生的应力是与结构的变形有关的，因此当改变约束部件间的弹性模量时，会导致结构间的变形状态改变，最终影响应力结果。

3 实例验证

以某核电厂化学和容积控制系统的混床除盐器设备力学分析为例，设备结构如图3所示，设备通过环板支撑件固定，环板支撑件通过螺栓连接固定在悬臂梁上。设备安全等级为3级，属于抗震Ⅱ类设备，设计压力为1 MPa，采用RCC-M规范D3300评价。RCC-M规范中对2、3级设备的二次应力不做评定。因此准确地判定二次应力的区域范围，可以减少设备的名义厚度，为设备减重，从制造和安装方面可以提高工程的经济性。

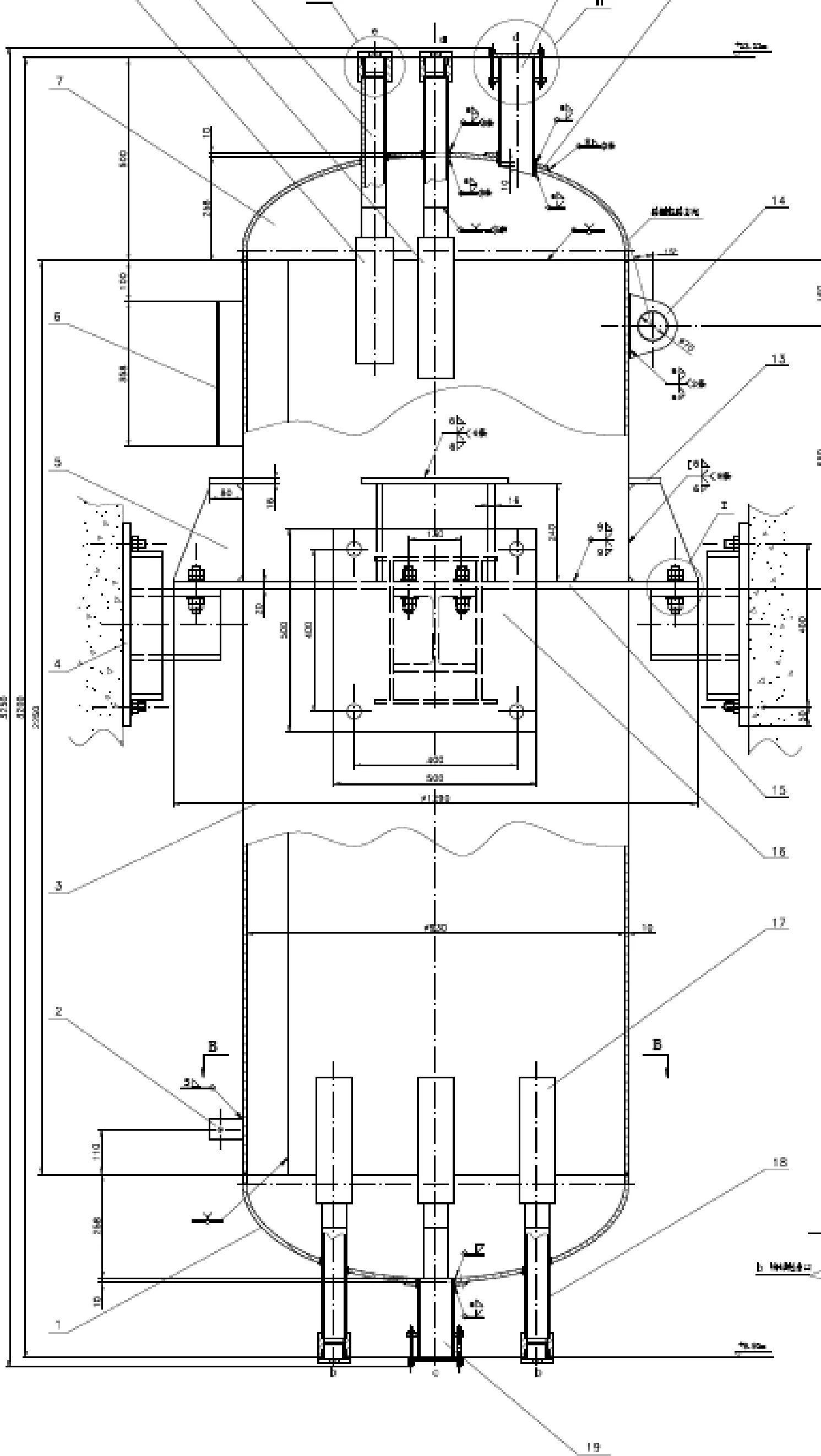
图3 混床除盐器结构简图Fig.3 Structure diagram of mix-bed desalinization

以压力工况为例，压力会导致设备轴向和径向的变形，但是环板通过焊接的方式与筒体连接，会限制筒体的变形，因此在环板与筒体连接处势必会存在协调变形，导致该区域应力过大，因此要判定二次应力的区域范围。

设备在承受设计压力时筒体环向应力最大，但为方便比较，本文参考轴向应力大小，根据理论公式可以得到设备筒体轴向的薄膜应力：

(1)

式中：σm——筒体轴向薄膜应力；

P——筒体内部设计压力；

D——筒体直径；

t——筒体厚度。

因此针对筒体轴向薄膜应力大于24 MPa的区域可将其划为二次应力影响区域。如图4所示展示了筒体薄膜应力超过24 MPa范围(灰度区域，但该区域同时存在倒角引起的结构不连续产生的峰值应力，但使用了壳单元无法获得峰值应力)。当调整筒体或者支撑的弹性模量时，该灰度区域会发生变化。当筒体的弹性模量增大时，灰度区域减小，下限应力值逼近24 MPa，这是由于筒体刚度得到增强，在内压下的变形减少，因此由变形协调导致的二次应力区域减小，减小的应力便属于二次应力。因此通过调整位移协调构件之间的弹性模量，可以获得二次应力的影响范围和大小。

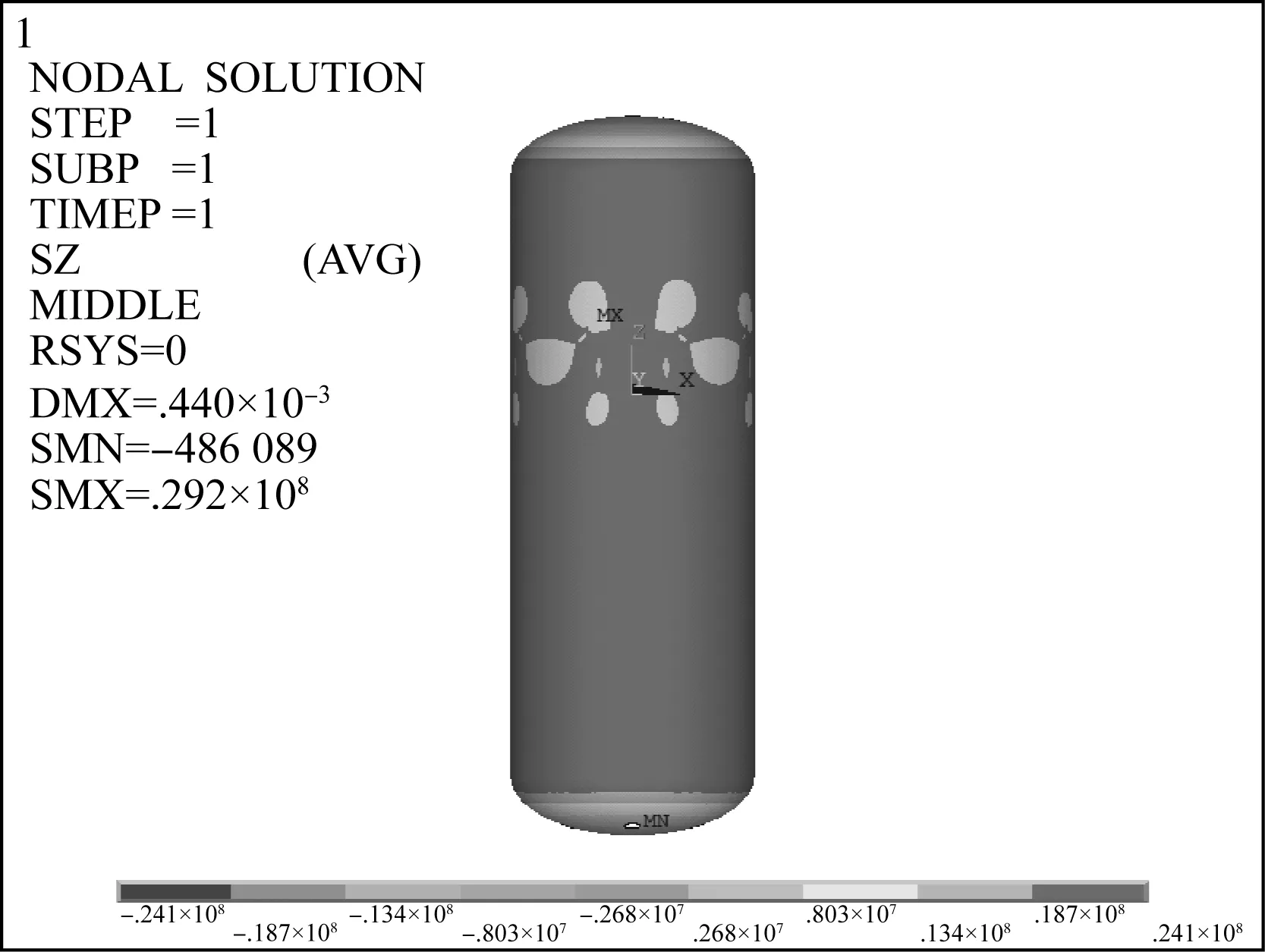
图4 二次应力影响区域范围Fig.4 Secondary stress affecting area

同理当支撑的弹性模量减少，筒体的薄膜应力也会逼近24 MPa，这是由于支撑的刚度变小，减少了对筒体变形的限制。虽然筒体或支撑的弹性模量有变化，但是由于内压产生的应力值是与结构的弹性模量无关的，因此筒体的一次应力仍然保持不变，但夹杂的二次应力会减少，从而最终结果接近理论值。

在处理部件变形协调导致的问题时，在不影响其实际约束的情况下，极限的状态下，可将部件去除或隔离，这实际上与之前提到的一次结构法类似。但在处理工程问题时，修改部件的弹性模量更为简单、方便。

需要注意的是，该方法的前提是建立在集中力、压力和自重等载荷导致的应力与结构的弹性模量无关基础上的，并不适用于温度载荷，应用应考虑其局限性。

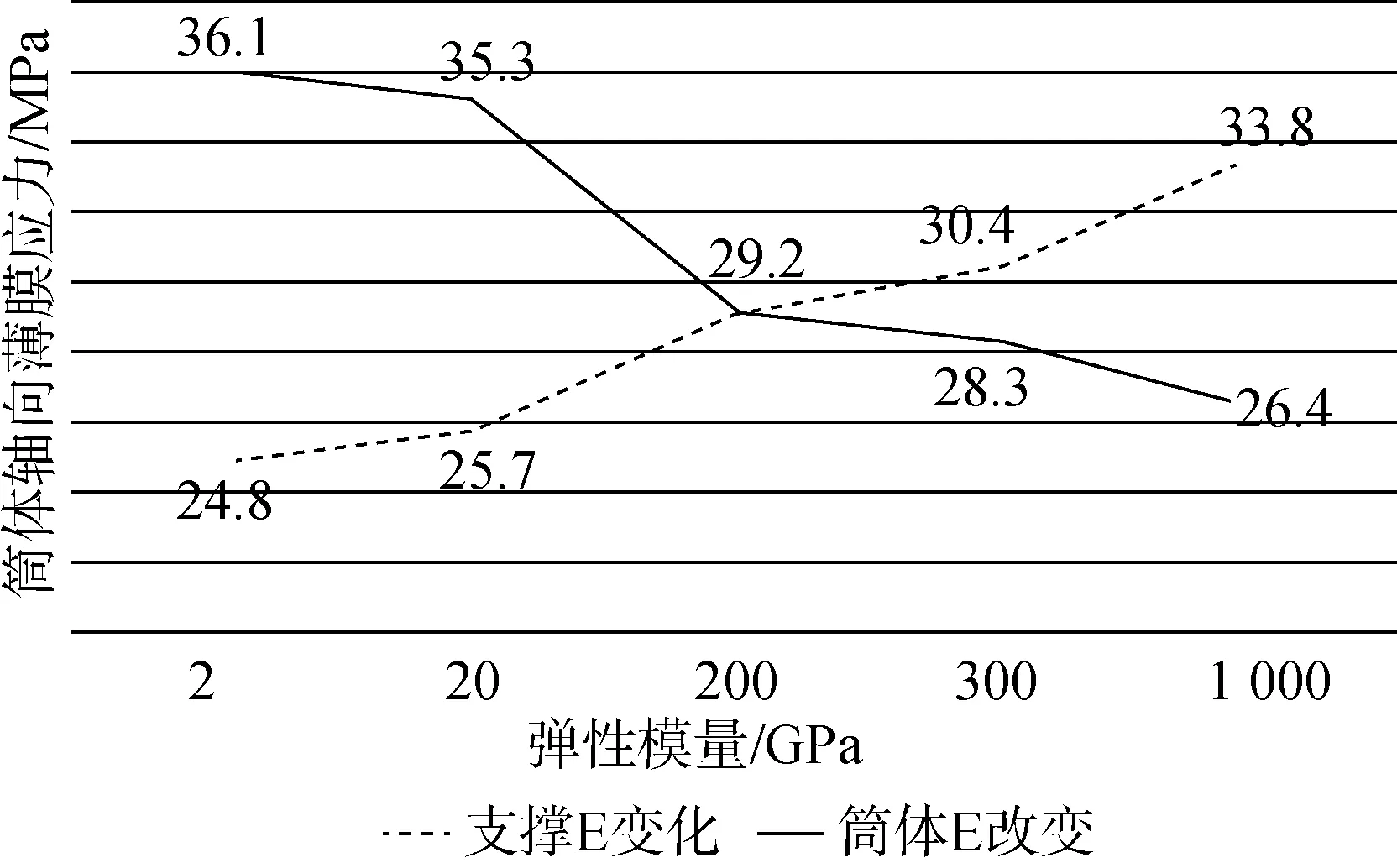
图5 筒体轴向薄膜应力随结构弹性模量(E)的变化曲线Fig.5 The plot of cylinder axial membrane stress versus structural elastic modulus

4 结论

文章介绍了压力容器设计分析中应力分类及原因，并且介绍了几种常见的区分二次应力的方法，最终引进了一种简易判定二次应力的方法，可以通过修改变形协调部件的弹性模量判定二次应力的范围。并应用一个设备分析实例阐述了原理及操作方法，证明了修改变形协调部件的弹性模量会影响结构的变形，从而导致二次应力的变化，根据其变化大小和范围便可以判定二次应力的区域。但该方法仅适用于判断集中外力、压力和自重等载荷产生的二次应力。