蒸汽发生器传热管流致振动非线性分析程序的开发与验证

周建秋，吕 红，何世贤

(中广核工程有限公司核电安全监控技术与装备国家重点实验室，广东 深圳 518172)

蒸汽发生器传热管的完整性对核电厂的安全性和经济性至关重要。蒸汽发生器传热管与支撑结构之间存在微小间隙，二次侧流体的横向冲刷引起的传热管振动会导致管壁磨损、疲劳失效甚至破裂。因此，蒸汽发生器设计过程中需要对二次侧流体横向冲刷引起的传热管的振动响应进行预测和分析。国外学者对核电厂蒸汽发生器传热管流致振动机理和传热管与支撑结构之间的微振磨损进行了大量理论和实验研究工作[1-6]。有些机构基于已有研究开发了专用的蒸汽发生器传热管流致振动分析程序，如加拿大Chalk River实验室的“VIBIC”程序[7]，可根据磨损功率和冲击力间的经验关系式预测传热管的长期磨损情况；B&W和EPRI于20世纪90年代通过大量实验获得合金690传热管的磨损系数，采用“SGFW”程序计算支撑板和防振条的磨损情况[8]；法国AREVA和CEA对传热管流致振动进行研究，于80年代开发了流致振动程序“GERBOISE”[9]。国外专用程序价格昂贵，且因无法获得源代码或知识产权问题等限制了使用范围。近年来，国内也有相关研究者采用商业软件针对蒸汽发生器传热管流致振动进行了分析计算[10-12]。然而，已有分析计算均是假设所有支撑为有效支撑的线性分析，未考虑蒸汽发生器传热管与支撑结构之间存在微小间隙的非线性振动响应以及微振磨损问题。

本文基于模态叠加法分析了湍流激励和流体弹性力作用下传热管的非线性振动响应，并自主开发了蒸汽发生器传热管流致振动非线性分析程序。以某核电厂蒸汽发生器传热管为例，分析了三种不同约束条件下传热管的非线性振动响应，并与GERBOISE程序的计算结果进行对比分析，验证了自主开发程序的正确性和有效性。

1 传热管非线性振动响应分析方法

蒸汽发生器传热管一般为薄壁的细长圆管，故可将其视作连续的欧拉-伯努利梁单元，这种单元忽略了旋转惯性矩和剪切变形效应。发生碰撞的传热管动态响应具有强烈的非线性效应，假设其非线性响应出现在传热管与支撑结构接触的位置。采用模态叠加法，将原动力学方程解耦得到模态空间动力学方程：

(1)

q——广义位移；

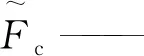
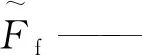
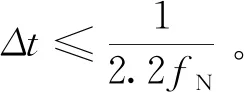
1.1 湍流激励

湍流力可视为沿管长方向在时间和空间上定常的随机力函数。由于随机湍流力是沿管长分布的，其广义力是对应每种模态下湍流产生的随机力[2]：

(2)

式中:Bk——k(k=x，y，z)方向的高斯白噪声；

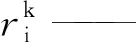
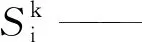
计算关系式为：

(3)

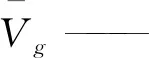
D——管道直径；

L——管道总长；

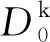
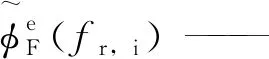
fr,i——简化频率；

ai——完全模态相关因子。

计算关系式为：

(4)

式中:φi(s)——第i阶模态振型；

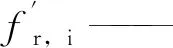
r(s)——沿管长方向的无量纲二次侧流体密度分布；

u(s)——沿管长方向的无量纲二次侧流体速度分布。

1.2 流体弹性力

流体弹性力采用Connors-Blevins耦合力模型[3]。假设有两根相同的传热管，其运动通过反对称刚性力耦合在一起，忽略不发生流弹失稳模态的广义流体弹性力，且只耦合同阶模态，计算关系式为：

(5-a)

(5-b)

式中:mi——第i阶模态质量；

ξi——第i阶模态阻尼比；

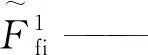
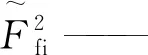
1.3 传热管与支撑结构间的接触力

由于传热管与支撑结构之间存在微小间隙，振动的传热管会与支撑结构发生接触碰撞或黏滞，并产生接触力，接触力作用在传热管上使其运动发生变化，故接触力随传热管的位置变化而变化[14]：

(6)

式中:Fn——法向碰撞力；

Ft——切向摩擦力。

采用“弹簧-阻尼”模型计算法向碰撞力。传热管与支撑板和防振条的接触模型如图1所示。

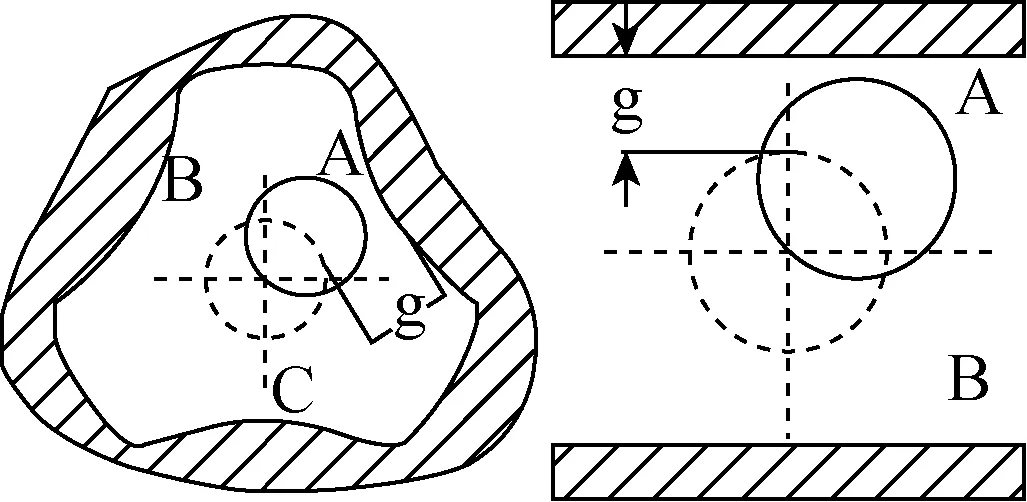
图1 传热管与支撑板和防振条的接触模型Fig.1 Tube-TSP and Tube-AVB structure contact model

当传热管的振幅大于间隙时，传热管与支撑结构发生碰撞，法向碰撞力为：

(7)

式中:Kc——接触刚度；

xn——传热管的法向位移；

g——传热管与支撑结构间的间隙值。

根据coulomb理论计算切向摩擦力：

(8)

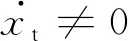
(9)

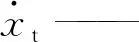
xt——切向位移；

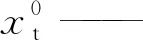
Kt——切向刚度系数，取

Kt=(1～10)Kc；

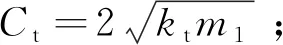
μd——动摩擦系数；

μs——静摩擦系数。

1.4 平均磨损功率

由于磨损是连续时间上的非线性运动，在运用动力学方程求解振动响应及碰撞时，可用平均磨损功率来统计连续时间内的磨损情况[2]：

(10)

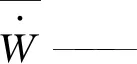
L(t)——经过时间T后的总的滑移位移。

2 程序开发

本文根据上述理论模型开发了蒸汽发生器传热管流致振动非线性分析程序。自主开发程序的核心计算代码采用Fortran语言编写，运行环境为Linux操作系统。程序计算流程图如图2所示。

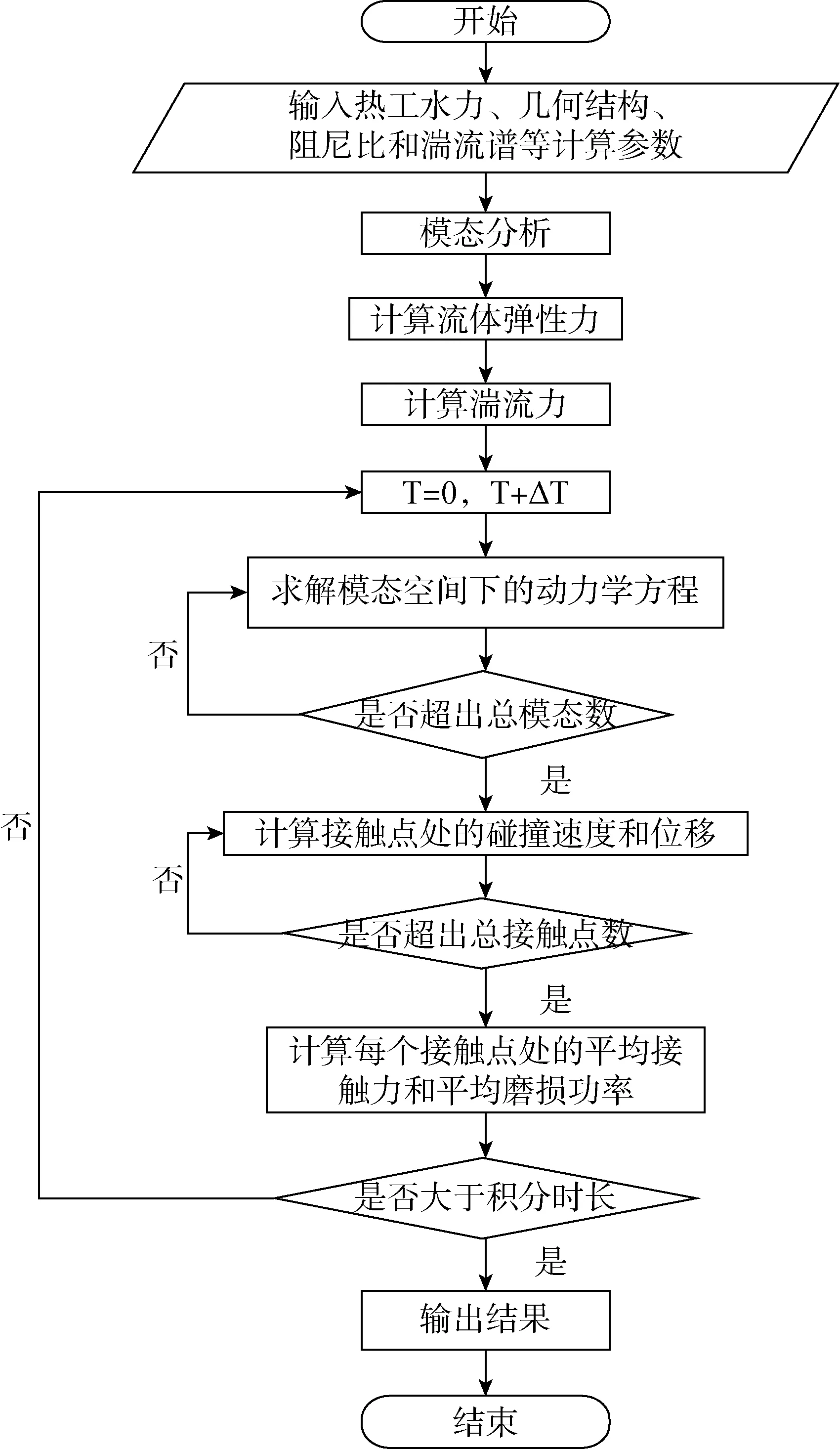
图2 非线性分析程序的计算流程图Fig.2 Flow chart of non-linear analysis program

3 算例验证

为了验证自主开发程序的正确性，本文对EPR核电厂蒸汽发生器某根传热管进行非线性振动响应计算，将计算结果与GERBOISE的计算结果进行对比分析。

3.1 典型传热管结构及参数

蒸汽发生器传热管的几何结构示意图如图3所示。传热管的详细设计参数为：管外径19.05×10-3m；管壁厚1.09×10-3m；传热管密度8 091 kg/m3；杨氏模量1.95×1011Pa；泊松比0.3；弯管处的弯曲半径822.9×10-3m；与该传热管接触的防振条数目为3；支撑板间距为1.094 m，共9块支撑板；传热管间距为27.43×10-3m；管板到第一块支撑板的距离为1.094 m；弯管中心到第9块支撑板的距离为0.097 m；传热管直管段总长度为9.943 m；传热管与防振条之间的间隙为0.053×10-3m；传热管与支撑板之间的间隙为0.285×10-3m。

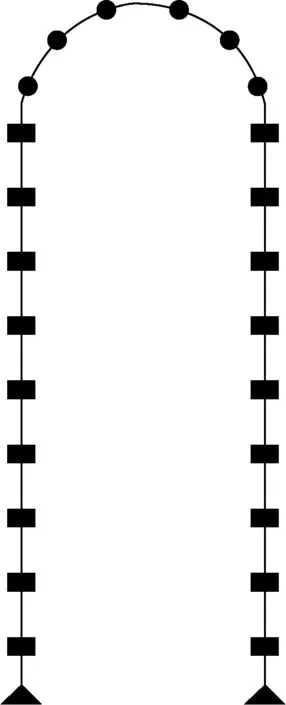
图3 传热管的几何结构示意图Fig.3 Schematic diagram of geometric structure of the tube

本文对三种不同边界条件下的振动响应进行分析：防振条处为间隙约束，支撑板处为简支约束；最上两层支撑板处为间隙约束，其他支撑板和防振条处为简支约束；最下两层支撑板处为间隙约束，其他支撑板和防振条处为简支约束。

3.2 计算结果

假设传热管与防振条之间存在微小间隙，支撑板处均为简支约束。传热管与防振条接触位置处的均方根位移的对比结果如表1所示。从表中可以看出，自主程序与GERBOISE的不同间隙处各个方向的均方根位移的计算结果吻合非常好，误差最大不超过1.5%。图4至图6是传热管与防振条接触点处的平均法向碰撞力、平均切向摩擦力和平均磨损功率的对比结果。从图中可以看出，自主程序计算得到的平均法向碰撞力、平均切向摩擦力和平均磨损功率与GERBOISE计算结果趋势一致，且吻合很好。自主程序与GERBOISE预测的最危险点出现在传热管同一位置，最大平均磨损功率分别为1.91×10-3W和1.89×10-3W，相对误差的绝对值为0.98%，图中接触点5和接触6点表示同一接触位置的两个不同接触点。

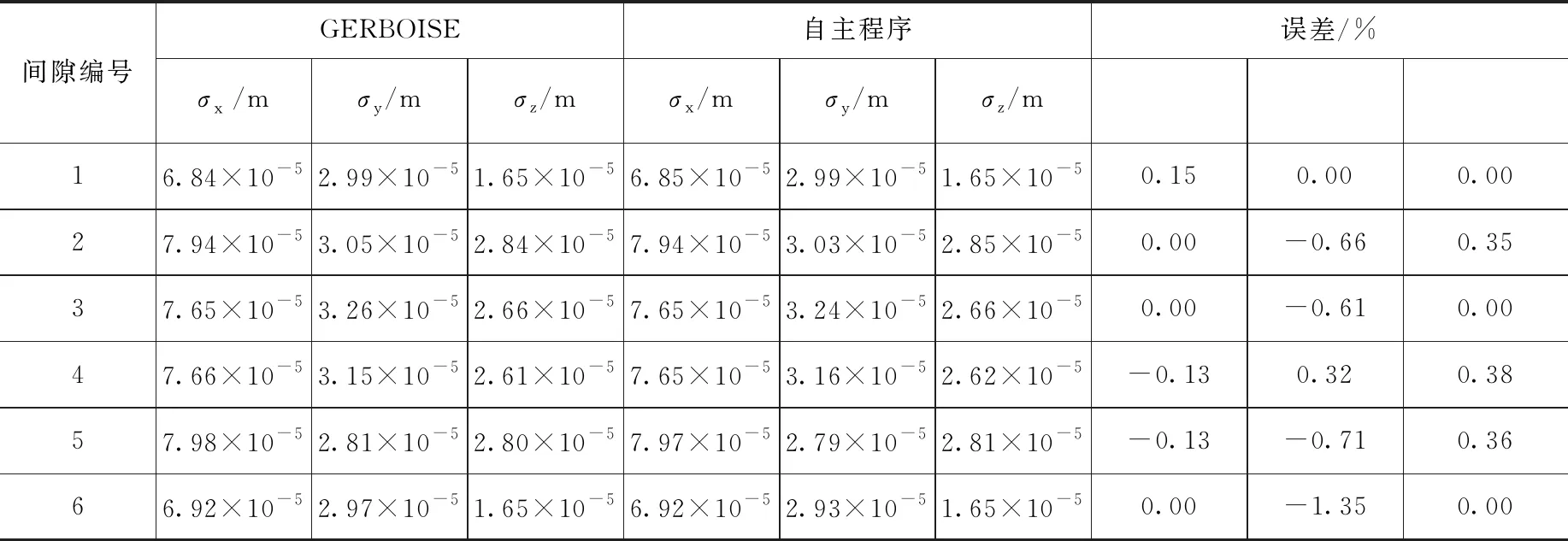
表1 不同间隙处的均方根位移Table 1 The root-mean-square displacements at different clearances

假设传热管与最上部两块支撑板之间存在微小间隙，其他支撑处均为简支约束。传热管与支撑板接触位置处的均方根位移的对比结果如表2所示。从表中可以看出，自主程序与GERBOISE的不同间隙处各个方向的均方根位移的计算结果吻合很好，最大振动幅度均出现在编号为2的接触位置处，且总的均方根位移的相对误差为1.9%。传热管与支撑板接触位置处的平均法向碰撞力、平均切向摩擦力和平均磨损功率对比结果如表3所示，表中的计算结果均表明传热管与支撑板未发生碰撞。

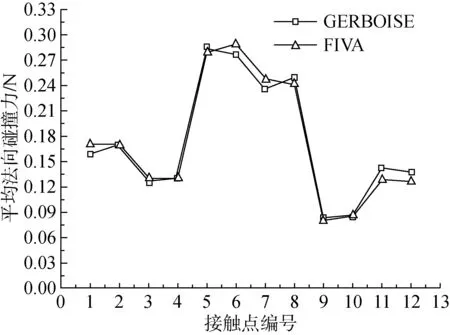
图4 接触点处的平均法向碰撞力Fig.4 Mean normal impact forces at contact points

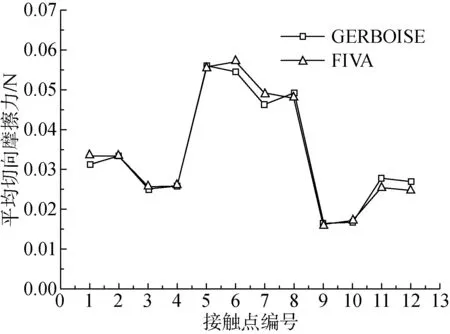
图5 接触点处的平均切向摩擦力Fig.5 Mean tangential forces at contact points

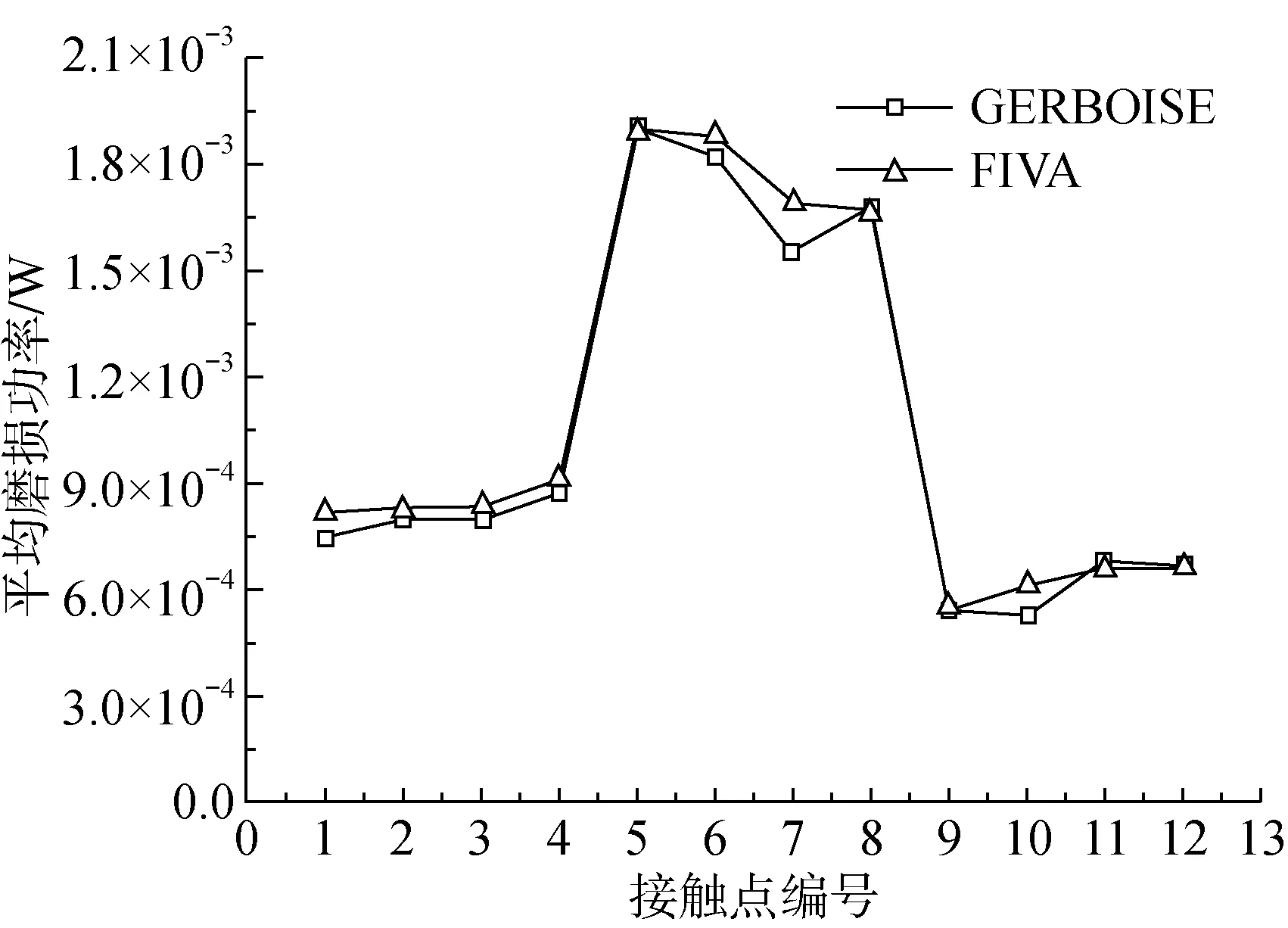
图6 接触点处的平均磨损功率Fig.6 Mean wear work rate at contact points

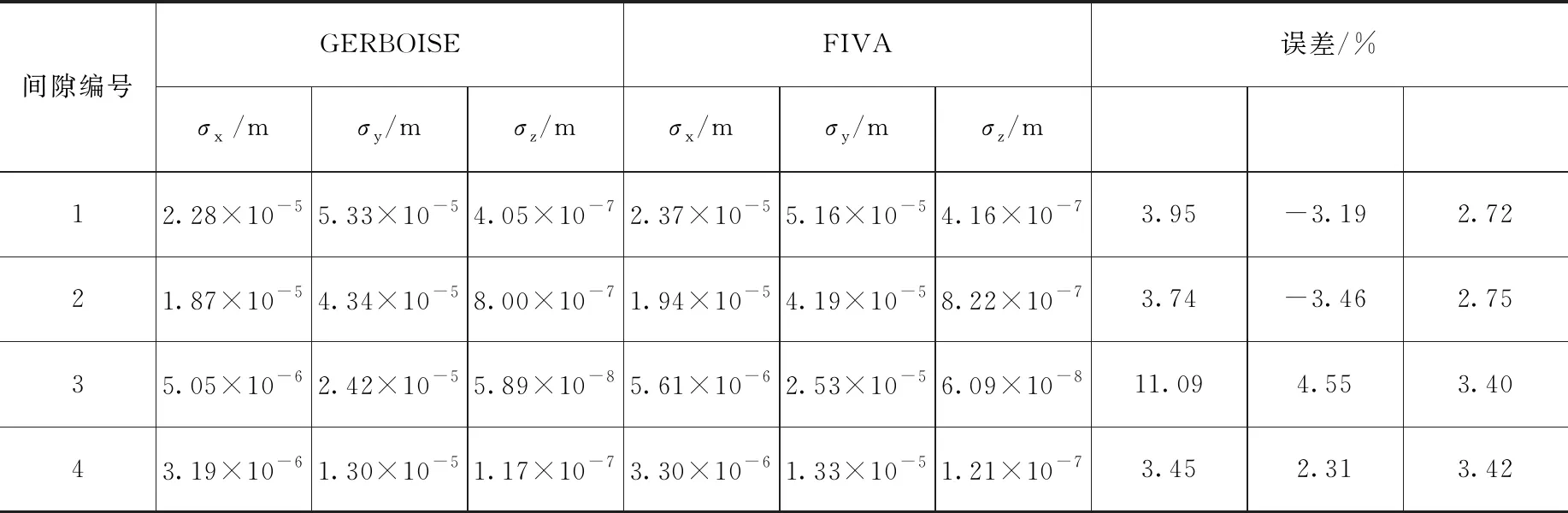
表2 不同间隙处的均方根位移Table 2 The root-mean-square displacements at different clearances

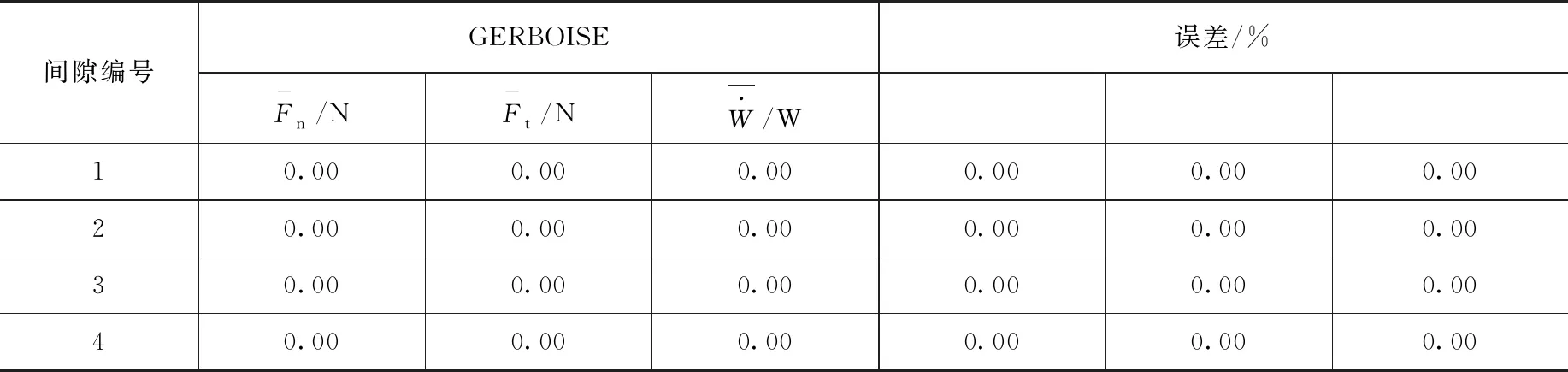
表3 不同间隙处的平均法向碰撞力、平均切向摩擦力和平均磨损功率Table 3 The mean normal impact forces,mean tangential forces and mean wear work rate different clearances

假设传热管与最下部两块支撑板之间存在微小间隙，其他支撑处均为简支约束。传热管与支撑板接触位置处的均方根位移的对比结果如表4所示。从表中可以看出，自主程序与GERBOISE的不同间隙处各个方向的均方根位移的计算结果吻合很好，最大振动幅度均出现在编号为2的接触位置处，且总的均方根位移的相对误差绝对值为1.22%。图7至图9为平均法向碰撞力、平均切向摩擦力和平均磨损功率的对比结果。从图中可以看出，自主程序计算得到的平均法向碰撞力、平均切向摩擦力和平均磨损功率与GERBOISE计算结果趋势一致，且吻合很好。传热管在接触点7～12处的平均磨损功率均为零，表明传热管在这些接触点处未发生碰撞。

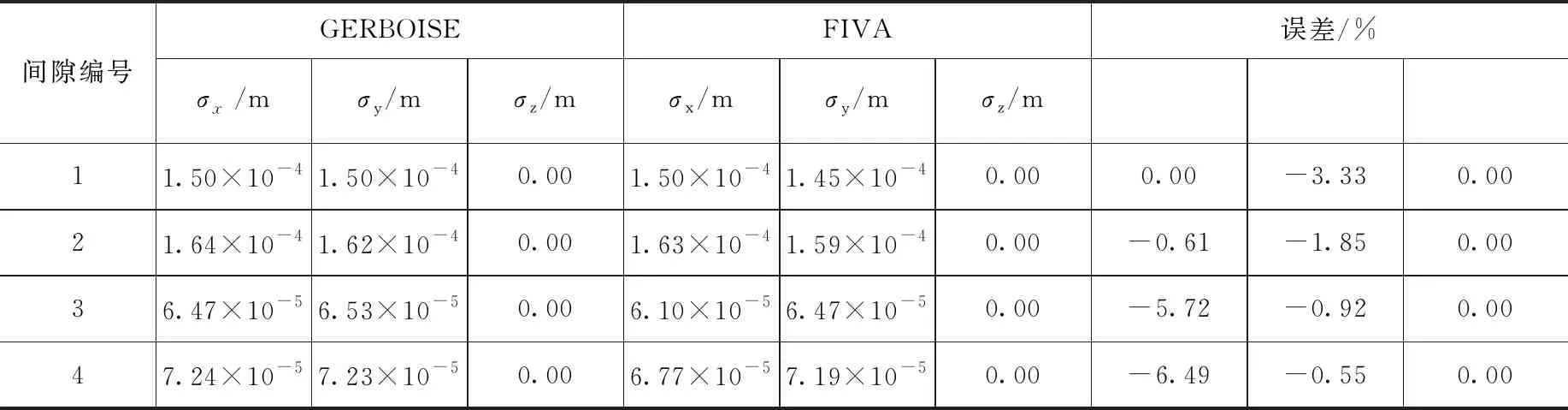
表4 不同间隙处的均方根位移Table 4 The root-mean-square displacements at different clearances

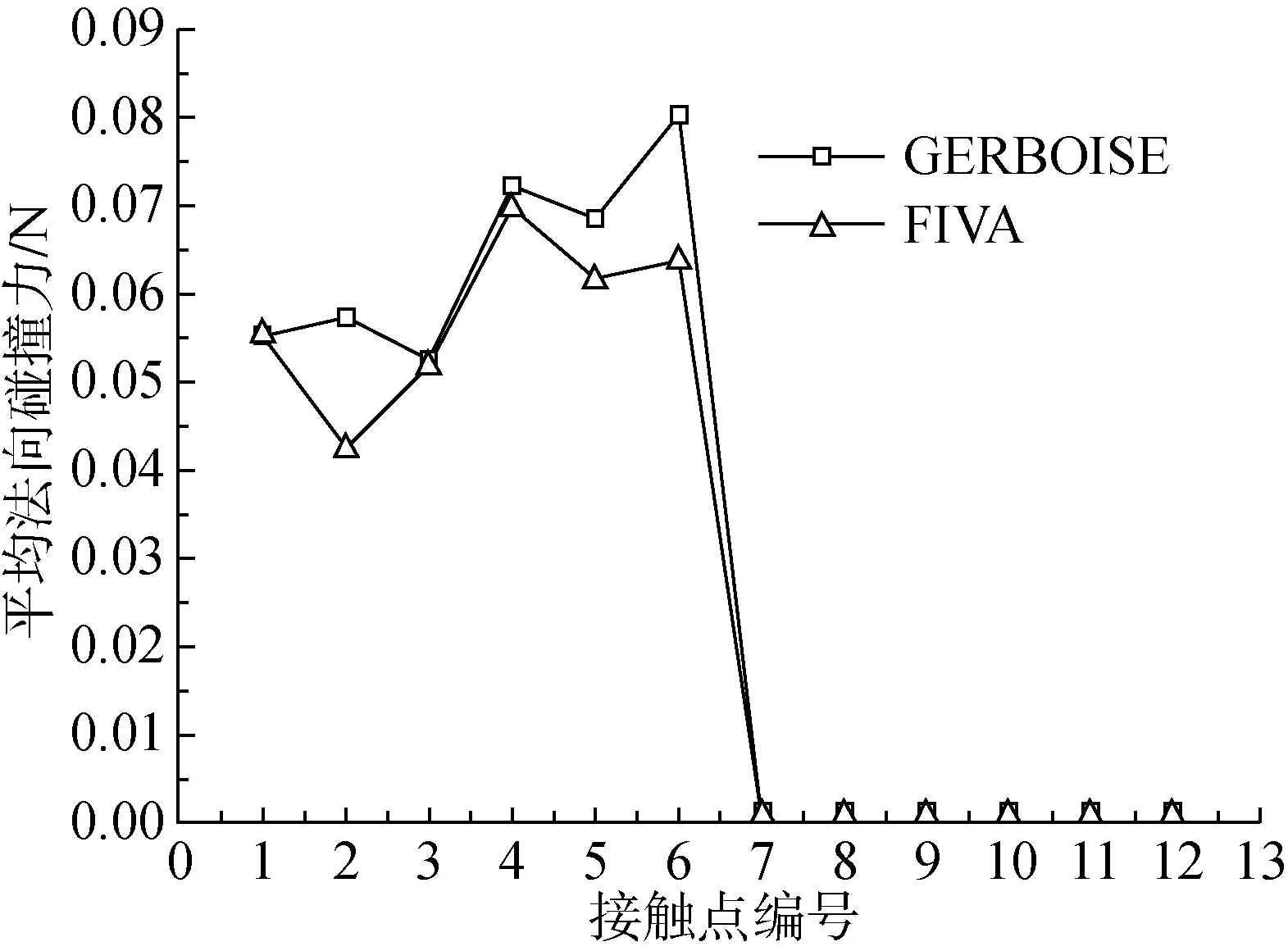
图7 接触点处的平均法向碰撞力Fig.7 Mean normal impact forces at contact points

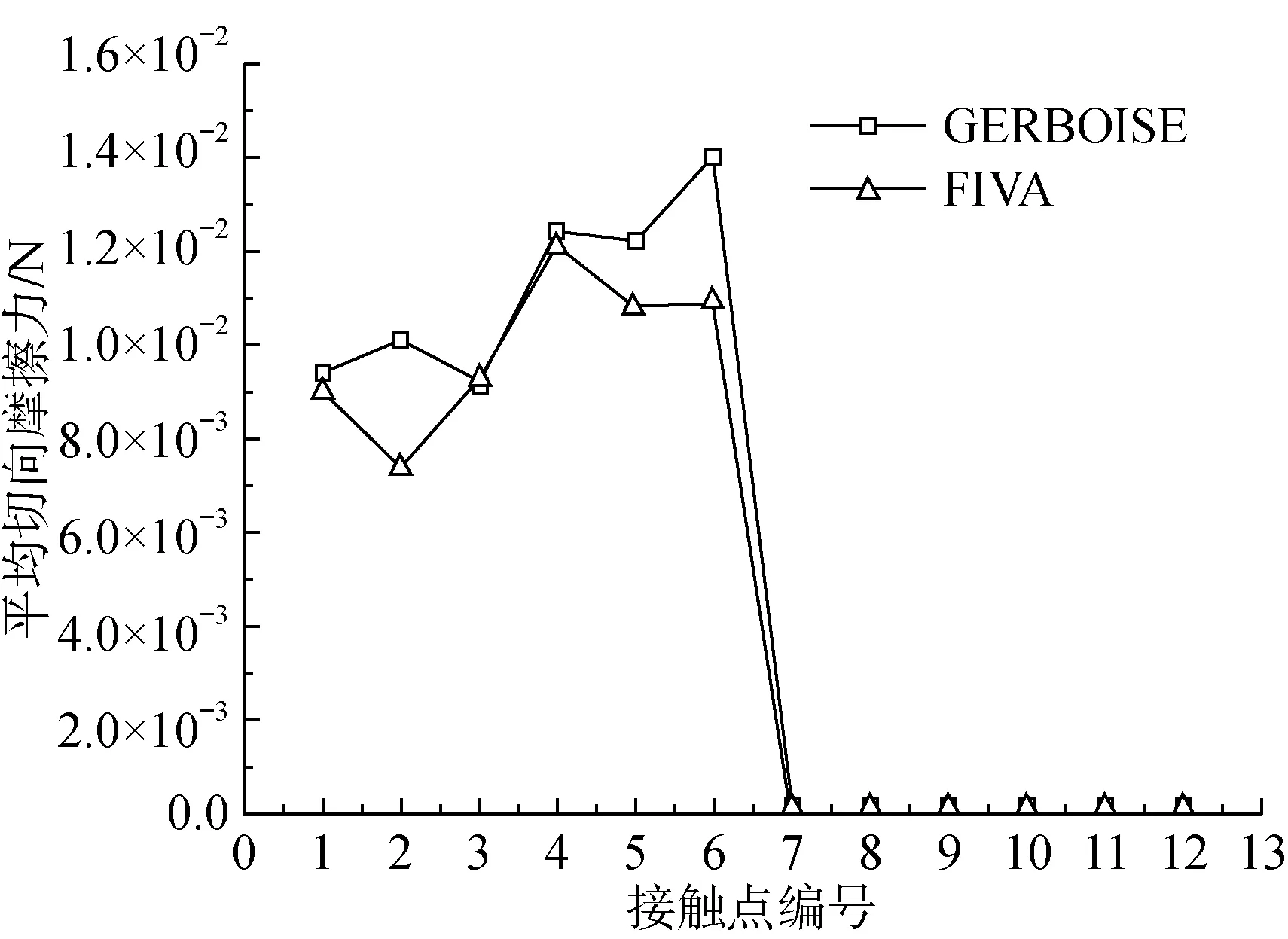
图8 接触点处的平均切向摩擦力Fig.8 Mean tangential forces at contact points

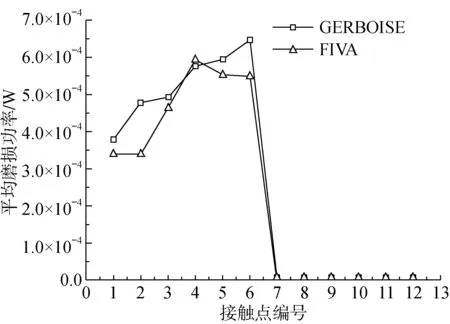
图9 接触点处的平均磨损功率Fig.9 Mean wear work rate at contact points

GERBOISE计算得到的最大平均磨损功率在接触点6处，自主程序计算得到的最大平均磨损功率在接触点4处。对于传热管而言，接触点4、5和6表示为同一接触位置，即磨损最为严重的位置均为编号为2的接触位置处。

4 结论

本文通过对适用于压水堆核电厂蒸汽发生器传热管流致振动非线性分析的理论模型进行研究，基于相应数学模型，自主开发了蒸汽发生器传热管流致振动非线性分析程序。通过将自主开发程序的计算结果与参考程序GERBOISE的计算结果进行对比分析可知，非线性分析得到的不同间隙处的均方根位移以及不同接触点处的平均法向碰撞力、平均切向摩擦力和平均磨损功率均吻合很好，平均磨损功率的最大值为传热管同一位置。自主开发程序可以用于蒸汽发生器传热管流致振动非线性响应分析，用于指导核电站蒸汽发生器传热管流致振动的设计，验证设计的合理性和有效性。