基于问题驱动的中职数学教学设计
2020-11-28李良
李良


[摘 要]由于数学具有高度的抽象性和缜密的逻辑性,而中职学生本身基础薄弱,学习习惯不佳,学习数学难度较大.教师可设计一系列问题串,以问题为驱动开展中职数学教学,从而培养学生的学习兴趣,激发学生参与的积极性,提升学生的学习效率.
[关键词]问题驱动;中职数学;教学设计
[中图分类号] G633.6 [文献标识码] A [文章编号] 1674-6058(2020)32-0009-03
对于多数中职学生来说,学习数学难度较大.笔者认为造成学生学习困难的主要原因,一是学生本身基础薄弱,学习习惯不佳;二是不少教师墨守成规,很少转变观念,很少研究新教法,不能有效地利用课堂.因此,教师最需要做的是不断地改善自己的教学方法,尽最大的努力去激发学生的学习兴趣.笔者结合多年的教学经验,认为基于问题驱动的教学方案不失为一种好的选择,此方案不同于传统教学,要求设计一系列问题链,由问题触发灵感,驱动教学,充分发挥学生的主体意识,提升学生的学习能力.
一、基于问题驱动的教学设计理论
问题驱动的教学理论要求教学的整个过程顺着问题展开,教学目标由问题引出,教学过程由问题激活,教学质量由问题表现,整个过程要紧紧围绕问题并基于问题解决来设计.问题及问题解决是教学设计的逻辑生长点,问题是数学的心脏,是思维的源泉和动力.
数学的真正组成部分就是问题和解.数学问题的解决离不开“好”的问题.因而好的数学教学设计应实现数学知识问题化,数学问题情境化和问题情境经验化.
数学教学中的问题包括外显的数学知识性问题和内隐的数学概念以及数学活动经验等生成性问题.在数学教学中既要使数学知识问题化,又要使数学问题意义化、形式化.借助问题把知识间的内在逻辑理顺连通,使学生的知识思维沿着问题“螺旋式”上升,从而完成知识的学习与理解.
问题是数学教学方向和动力生成的核心要素,教学过程实质上是基于问题解决的学习过程.好的问题能够启迪思维,激发好奇心和求知欲,活化思维过程,从而产生创造性思维.通过不断地思考、探究,促进学生对知识的理解和巩固,进而培养学生解决问题的能力 .
二、基于问题驱动的教学过程
(一)教材分析
笔者所选教材为《数学(基础模块)》(高教版),本节课为教材第5章《三角函数》第4节中的第一部分内容.在学习本节课内容之前,学生已经学习了任意角的三角函数的定义、各象限角的三角函数值的正负号取法等内容.学生对三角函数的知识有了一定的了解,这为本节课的学习打下了很好的知识基础.本节课的知识是上述内容的继续,也是后续课程的必要基础,起着承上启下的作用.它将在三角函数研究中发挥关键性的作用,而基本关系式是三个三角函数的纽带,为今后三角函数的研究提供有力保障.同时通过学习本节内容,可以培養学生的计算能力和数学思维能力,提高学生分析与解决问题的能力 .
(二)教学目标
1.通过三角函数定义,导出同角三角函数的基本关系.
2.中职同角三角函数的基本关系式主要应用是求值,能做到知一求二.
3.通过同角三角函数关系的应用使学生养成探究、分析的习惯,树立分类讨论、转化与化归的思想方法.
(三)教学过程
1.复习引入
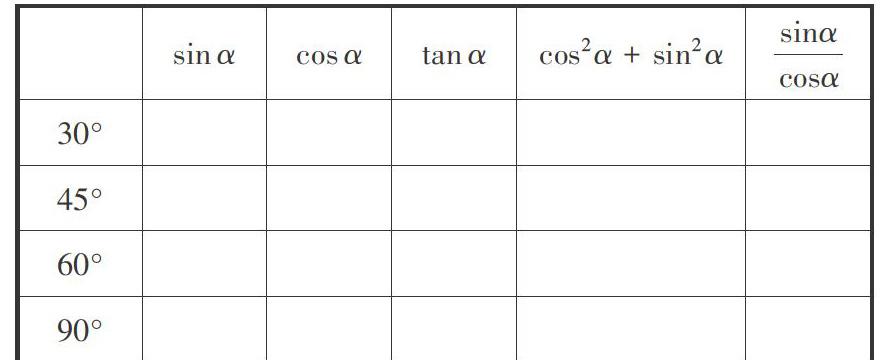
问题1:上面的表格你能填一填吗?根据上面的表格能否得出同一个角[α]的三个三角函数之间有一些什么关系?
设计意图:使学生能简洁明了地从特殊值体会基本关系式,降低难度,激发兴趣,启迪思维.表格的设计,一是给学生以直观感受,二是复习原有的知识,检查学生已有知识的掌握程度,巩固基础.
2.新课探索
问题2:上节课我们已学习了任意角三角函数的定义,如图1所示,任意角[α]的三角函数是如何定义的呢?
三、教学设计的几点反思
第一,教学设计要立足于学生实际.中职学生的数学基础相对较差,教案的设计要结合他们的特点,习题难度要适中,易于理解.不然将无谓增加学生负担,打击学生自信心,从而无法完成既定的教学目标.因此在本设计中避免了难题、怪题,以基本题型为主,使学生易于掌握,方便改编,增强学生信心,调动学生积极性.
第二,任何科学研究都要经历提出问题、分析问题和解决问题的过程.即科学问题都是由问题驱动的.本次教学设计的主线是用问题来引导,通过一系列的问题串推动整个知识的教学.笔者从已有知识点的复习巩固入手,激发灵感火花,猜想基本关系式,继而运用已有知识求证基本关系式,进而再从既定关系式转到实例运用,最后让学生创造性地编题、讲题,由简到繁,层层递进.让学生体验从特殊到一般的认知过程,并在此过程中体会转化与化归、分类讨论等思想.教学中,笔者努力创设合适的问题情境,激起学生的求知欲,促进思维活动的开展,完成知识的学习积累.
第三,在教学最后的互动环节,笔者加入了变式教学的尝试. 一堂好课应体现教师的引导作用,强调学生的主体地位.教师以往的“填鸭式”教学模式无疑削弱了学生的这个地位,如果学生只会依样画葫芦地解题,缺乏主动求变的能力,会造成实际教学效率的低下,效果不佳.因此,这类教育目前正在被摒弃.而采用变式教学模式,教师将变成教学活动的组织者和指导者,探讨的问题由教师引发,进展由学生决定,把学习的主动权交还给了学生.
鉴于本节课的内容在后期学习的重要性,笔者要求学生熟练掌握所举例题的方法,故笔者采用了变式教学.不同以往,在本次互动活动中笔者希望学生主动求变,不论是变题设还是变问题,改编的权力将完全由学生自行把握.通过这个过程让学生学会换位思考,从不同角度根据内容编题、说题,从更高、更深的角度来理解知识,掌握思考方法.
[ 参 考 文 献 ]
[1] 王佩,赵思林.基于问题驱动的数学教学设计:以“任意角的三角函数”为例[J].中学数学月刊,2017(10):17-20.
[2] 李广全,李尚志.数学(基础模块)[M].北京:高等教育出版社,2018.
(责任编辑 黄桂坚)
