改进相关向量机的短波信道盲均衡算法研究

2020-11-27温泽馨白立云

舰船电子对抗 2020年5期

温泽馨，白立云

(武汉船舶通信研究所，湖北武汉 430020)

0 引言

由于短波信道中存在幅度衰落、多径时延、多普勒频移和噪声干扰等因素影响[1]，所以信道传输的条件变得十分复杂[2]。接收端接收到的信号会受到干扰，接收码元之间产生重叠，即产生了较大的码间干扰(ISI)。码间干扰会影响信道的传输效率并且会增大误码率，因此一种用来校正和补偿系统特性的可调滤波器被插入系统中，使得码间干扰的影响得以降低[3]，并使得发送信号的恢复成为可能。我们将起补偿作用的可调滤波器称为均衡器[4]。自适应均衡技术需要已知训练序列的相关参数，但是在非协作通信中，接收端获得信号的先验信息通常被认为是不可能事件[5]。盲均衡算法可以使得在码间干扰消除的同时不使用训练序列[6]，因此，盲均衡算法成为非协作通信系统领域的研究热点之一[7]。

1 常用盲均衡算法

从Sato提出“自恢复”即盲均衡技术开始[8]，盲均衡算法已发展为四大类[9-10]。根据盲均衡过程中使用的不同优化方法和不同数学理论模型进行划分，这四大类分别为：Bussgang类盲均衡算法，基于二阶及高阶统计量盲均衡算法，基于信号检测理论盲均衡算法和基于人工智能方法的盲均衡算法[11]。

在盲均衡的研究中，支持向量机(SVM)算法由于其出色的学习性能，在样本维数高、非线性均衡问题中被广泛应用[12]。但是支持向量机算法以一个决策结果而非后验概率作为输出，回归问题的参数ε必须使用交叉验证等方法确定，而且要求核函数必须是正定的[13]，这对它的使用造成了限制。以SVM的形式为基础，使用贝叶斯框架，Tipping于2001年提出了一个新的可以用于回归问题和分类问题的贝叶斯稀疏核方法[14]，即相关向量机(RVM)。相关向量机中，用于训练和预测的模型是基于贝叶斯框架构建起来的，以贝叶斯原理为基础，得出一个可以使协方差最小的高斯过程模型[15]。这一算法通常可以得出更稀疏的预测结果和更小的误差。RVM在盲均衡方面的出众性能已经得到了验证[16]。

传统的单核相关向量机，无法充分利用不同类型核函数的优势，有的核函数插值能力较强，有的核函数外推能力较强，单核函数无法兼顾这些优点。因此多核学习(MKL)方法[17]被提出,以改进RVM的学习效果。基于以上讨论，本文提出使用多核函数[18]作为相关向量机的核函数，其系数采用量子粒子群优化(QPSO)算法[19]进行寻优得出。

2 MKRVM盲均衡算法

2.1 均衡系统模型

图1是均衡系统模型，原始发送信号用x(n)表示，信道用h(n)表示，信道输出信号为y(n),也即盲均衡器的接收信号。为了消除码间干扰，使输出信号y(n)经过均衡器，恢复出发送信号x(n)。

均衡器的接收信号为：

y(n)=h(n)*x(n)+n(n)=

(1)

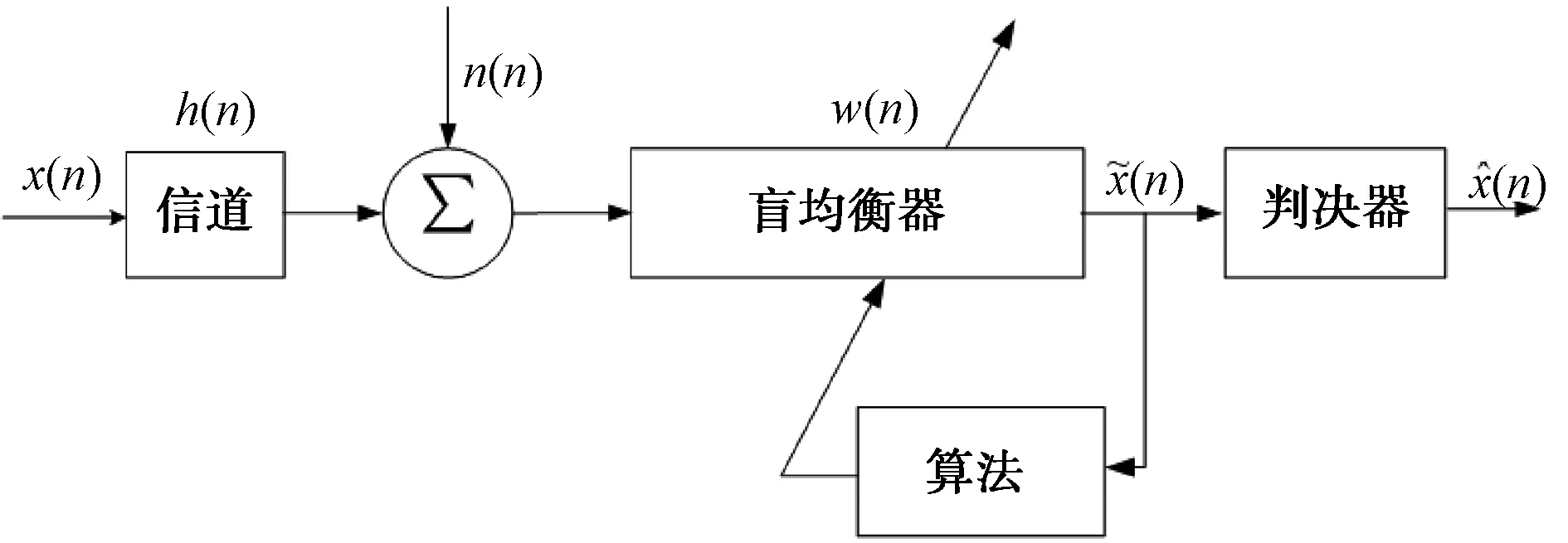
图1 均衡器系统模型

2.2 QPSO算法

粒子群优化(PSO)算法是一种以群体协作为基础的随机搜索算法，它是通过模拟鸟群觅食行为而发展起来的。PSO算法的基本假设是：每个粒子都有一个对应的速度和位置参数，通过进化计算求解最优解[20]。QPSO算法对粒子群算法进行改进，取消了速度参量，增加了位置中心点，引入量子行为，一方面减少了需要设定的参数[21]，另一方面增加了粒子位置变化的随机性[22]，避免陷入局部最优的情况。

假设一个粒子的个体最优位置用Ph来表示，那么它的位置判别公式为：

(2)

式中：Xh为粒子h的位置；t为迭代次数；f(x)为适应度函数，在实际应用中需要最小化。

然后计算全局最优位置：

Pg=argmin{f(Pj)}

(3)

进一步迭代：

(4)

P=aPh+(1-a)Pg

(5)

(6)

式中：Z表示粒子群的大小，个体最优位置的平均值即平均的历史最好位置，被称为中心位置，用式中的zbest来表示；c为压缩扩张因子；a和b为随机数，是(0,1)上的均匀分布数值[23]，取正数和负数的概率均为0.5。

由以上的推导过程可以看出，QPSO算法中只有c这个参数需要人为设置，一般c的值不大于1。将多核学习相关向量机的各个核函数的系数映射为粒子的多维位置中的一维，系数数量等于位置的维度，基于QPSO的系数寻优算法步骤如下：

Step1：参数初始化。

Step2：设置均方误差(MSE)的值为适应度函数的值，由此生成各个粒子的适应度，根据式(2)和式(3)计算每个粒子的个体最优位置和全局最优位置。

Step3：根据式(4)计算中心位置zbest。

Step4：根据式(5)和式(6)计算每个粒子的新位置。

Step5：重复进行Step1～Step4的过程，直到算法设定的最大迭代次数，全局最优位置即为各个基本核函数的系数。

2.3 MKRVM算法用于盲均衡

假设输入信号集用si来表示，令其通过图1所示的盲均衡系统，则均衡器的输出为：yi=wTxi，由此得样本的目标向量为：

(7)

根据贝叶斯模型可得：

(8)

式(8)中，权重系数用w=[w1,w2,…,wM]来表示。用于回归的RVM表达式为：t=φw+ε，为了求得合适的w值，有：

t=φw+ε=y+ε

(9)

式中：φ为判决矩阵；根据均方误差准则，ε为相互独立的噪声，均值为0，方差为σ2。

假设t是独立分布的，则t的高斯似然可以表示为：

(10)

式中:yi的最高次项是四次，为了使式(10)的形式适合用来构建RVM模型，需要将四次项进行改写：

(11)

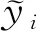
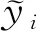
(12)

为避免过拟合现象的发生，每个权重系数w被1个一一对应的先验概率α来限制，这里的α即为超参数。权重系数的后验概率为：

N(w|μ,Σ)

(13)

在式(12)中，协方差：

(14)

均值：

(15)

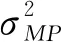
(16)

令式(15)中对α求得的偏导数为0，并进行化简，可以得出：

(17)

式中：μi为第i个后验权重系数的均值；γi=1-αiΣii，后验协方差矩阵Σ的第i个对角元素用Σii表示。

令式(16)中对σ2求得的偏导数为0，并进行化简：

(18)

不断重复以上步骤进行迭代，最终的预测值由y=Φμ得出。

Step1：首先对σ2和α的值进行初始化：σ2=var(xi)×0.1，α=(1/M)2。

Step2：计算协方差和均值，利用式(13)和式(14)进行计算，得出Σ和μ。

Step3：利用式(16)和式(17)进行计算，得出αi和σ2。

Step4：若本次迭代后得出的αi接近无穷大，则去除对应的基函数。

Step5：重复以上步骤直至算法达到收敛条件。

Step6：求出最终的预测值y=Φμ。

3 仿真测试

3.1 实验参数

本文中的实验采用MATLAB2016仿真工具箱实现模拟测试，使用8PSK调制信号，信号长度为200，短波信道条件参考国际无线电咨询委员会给出的短波深度衰落信道参数条件。有2条路径，路径1和路径2的时延分别是0 ms、2 ms，信道增益均为1，多普勒频移均为1 Hz，多普勒扩展均为0 Hz。迭代50次的结果如图2、图3所示。

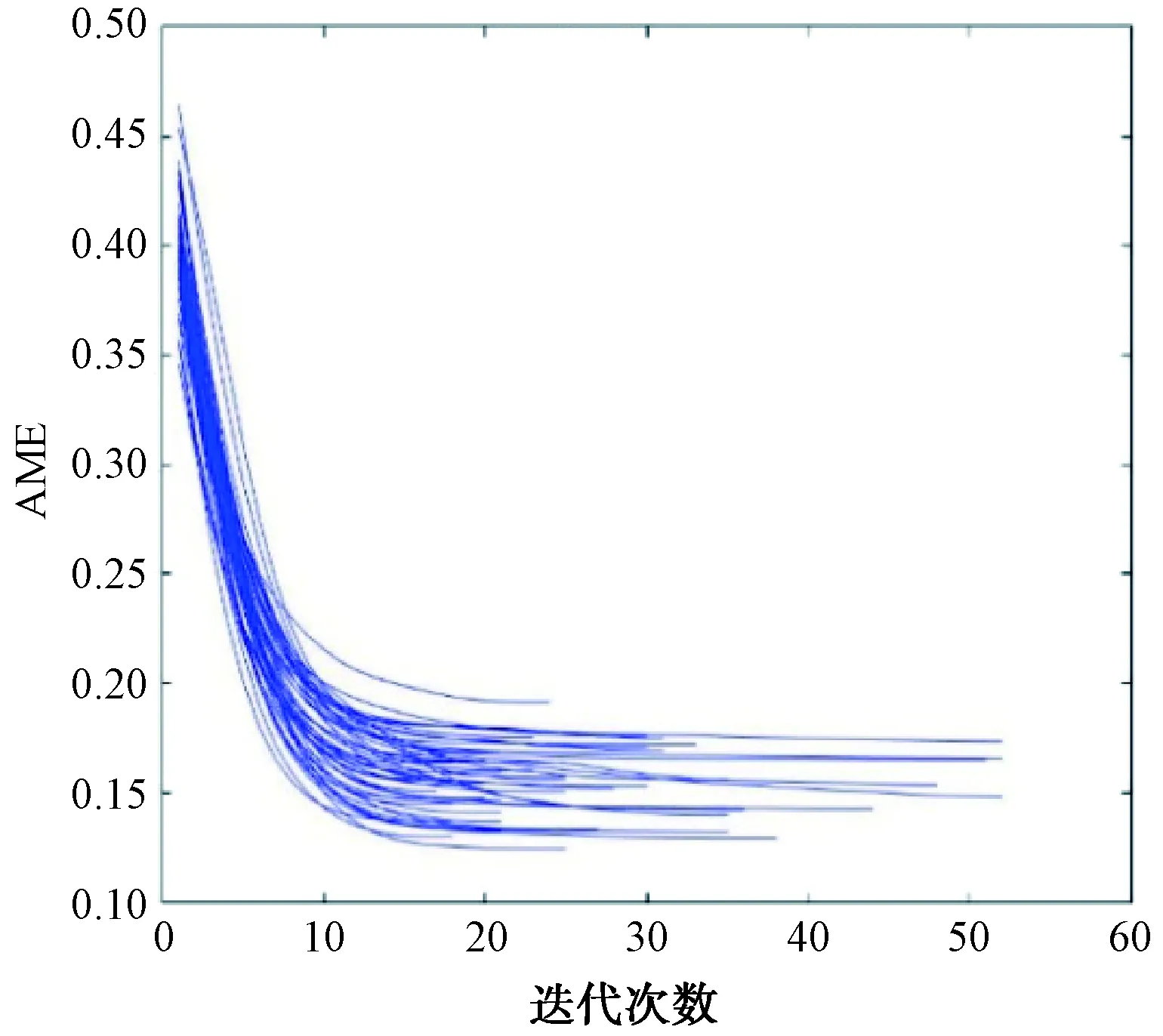
图2 RVM盲均衡的AME误差曲线图

图3 MKRVM盲均衡的AME误差曲线图

图4、图5为多核相关向量机、相关向量机、支持向量机3种算法在相同条件下的AME误差、误比特率曲线对比图。

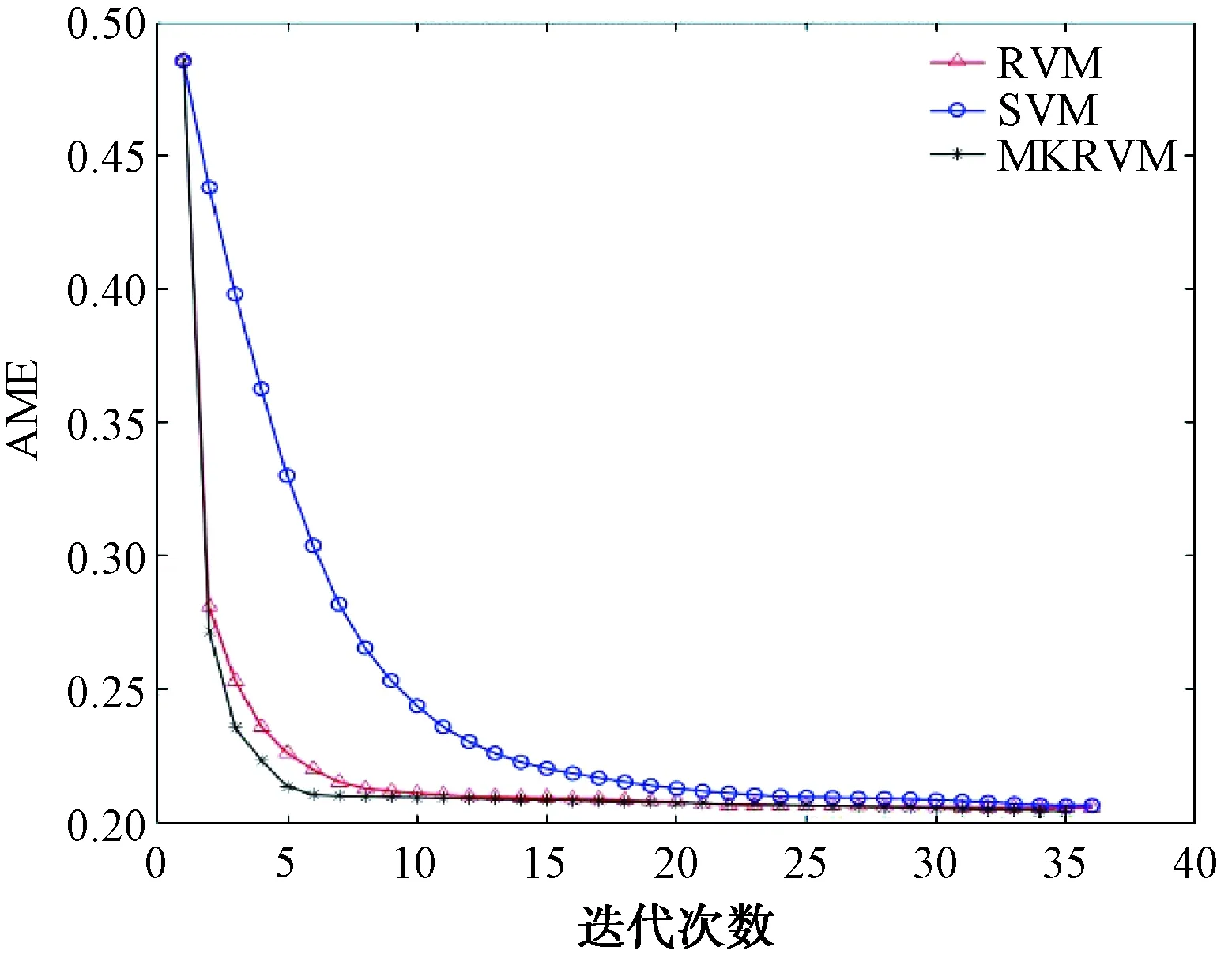
图4 MKRVM/RVM/SVM的AME误差曲线对比图

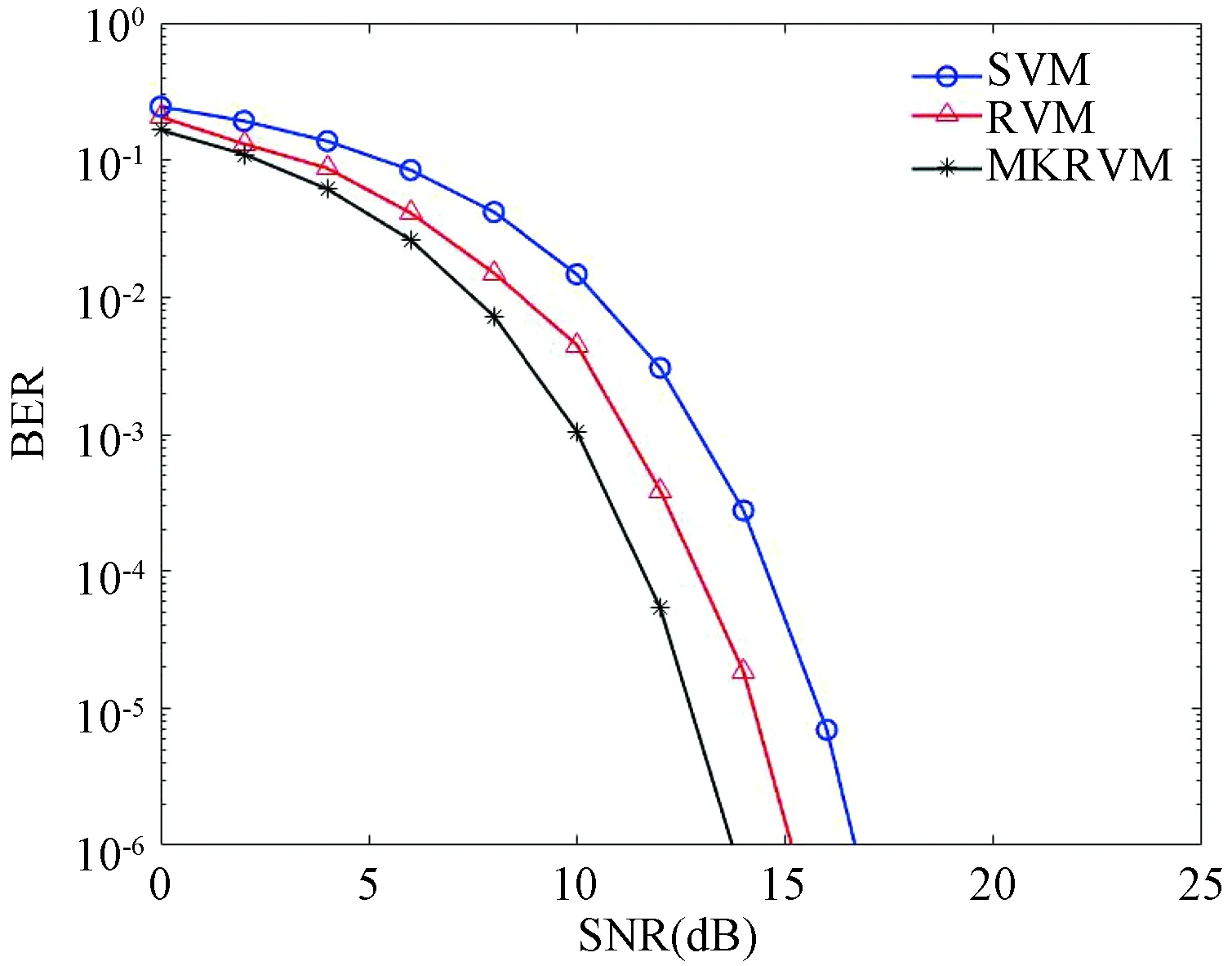
图5 多核相关向量机、相关向量机、支持向量机盲均衡算法的BER曲线对比图

3.2 结果与分析

对不同信噪比下支持向量机、相关向量机、多核相关向量机稀疏性进行对比，结果如表1所示。

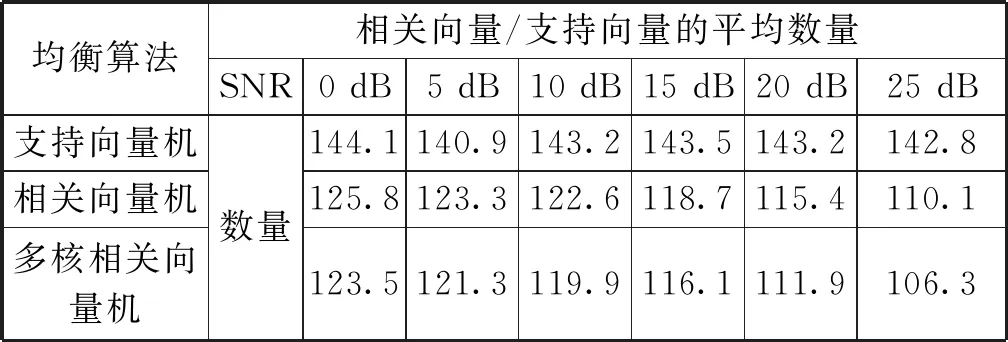
表1 不同信噪比下支持向量机、相关向量机、多核相关向量机稀疏性对比

由仿真结果可以看出，与RVM盲均衡的结果相比，MKRVM盲均衡最终得出的误差比RVM低，而且具有更好的稳定性和稀疏性，这证明了多核函数比单核函数具有更好的性能。支持向量机算法比起另外2种算法稀疏性较差，而多核相关向量机算法比起经典的单核相关向量机，稀疏性又有所增强。在仿真或实际应用过程中，稀疏性好的算法可以更快地收敛。此外，多核相关向量机和相关向量机得出的误比特率远远低于支持向量机盲均衡算法，而且多核相关向量机得出的误比特率始终低于相关向量机，说明这一算法更适用于短波信号的盲均衡。