基于信道分类分析的无线通信改进均衡方法

2022-08-23方振宇闻建刚蔡一再邹园萍华惊宇

杭州电子科技大学学报(自然科学版) 2022年4期

方振宇，闻建刚，蔡一再，邹园萍，华惊宇

(浙江工商大学信电学院，浙江杭州 310018)

0 引言

无线通信中，信号经过多径信道时，易产生码间干扰，造成误码。在通信系统的基带或中频部分插入均衡器可减少码间干扰。文献[1]提出一种改进的差分进化算法,增加动态参数调整机制，有效补偿了衰落信道引起的信号畸变。文献[2]提出一种基于基追踪降噪的自适应均衡算法，利用稀疏多径信道下均衡器权值的稀疏性，将自适应均衡器的训练过程看作是压缩感知理论中稀疏信号对字典的加权求和，并运用重构算法直接对稀疏权值进行求解，提高了稀疏多径信道下算法的性能。文献[3]设计了一种基于变步长算法的线性自适应均衡器，缓解了信号传输中多径效应的影响，改善了信道均衡的效果。目前，大多研究是通过改善均衡器本身的均衡效果来减少码间干扰，往往忽略了信道系数对均衡器均衡效果的影响[4-6]。本文主要研究信道系数变化趋势对均衡效果的影响，使用适宜的求逆方法得到合理的均衡器系数，从而提升均衡器的均衡效果。

1 时域均衡器TEQ基本原理

假设时域均衡器(Time Domain Equalizer，TEQ)处于理想状态，均衡后的理想等效信道为：

(1)

式中，hk表示均衡后的等效信道，wn表示抽头系数，xn-k表示输入信号。

对抽头系数和输入信号进行Z变换，得到合成系统传递函数抽样序列的Z变换表达式为：

H(Z)=GE(Z)X(Z)=1

(2)

式中，GE(Z)表示横向滤波器传递函数抽样序列的Z变换，X(Z)表示原函数传递函数抽样序列的Z变换，H(Z)表示合成系统传递函数抽样序列的Z变换。

转换为如下矩阵形式：

(3)

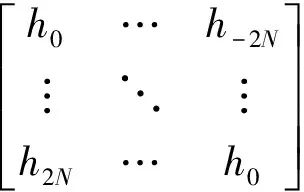
2 基于信道分类的均衡效果设计方案

时域均衡算法采用的是求逆操作。在凸峰型信道中，信道系数变化趋势呈先升后降形式，直接求逆会导致奇异矩阵问题，可采用广义求逆方法恢复均衡，但广义求逆增加了一定的运算复杂度，因此，本文对信道系数的托普利兹矩阵条件数进行分析，用于判别用直接求逆还是广义求逆方法。

固定信噪比(Signal-To-Noise Ratio，SNR)，信道系数向量的功率延时包络(Power Delay Profile，PDP)服从常数a决定的指数分布形式e-at。信道系数向量长度为6时，常数a有2个值，即a=1.0(弱指数)和a=1.5(强指数)，信道方差归一化为1。未归一化的无噪信道向量为：

hc=randn(1,Lh).*P+j×randn(1,Lh).*P

(4)

式中，Lh表示信道长度，P表示信道PDP向量，j表示虚数单位，.*表示向量对应位置元素的乘积。将无噪信道归一化，得到：

hn=hc/norm(hc)

(5)

SNR的倒数即为噪声方差，

nv=1/SSNR

(6)

式中，nv表示噪声方差，SSNR表示SNR的值。噪声向量为：

(7)

将噪声向量和归一化后的无噪信道相加，得到信道估计向量为：

hh=hn+z

(8)

对TEQ长度进行遍历，遍历范围为：

Lf=Lh×2+1∶2∶10×Lh

(9)

均衡器长度Lf∈[13,60]。

(10)

式中，SSINR表示均衡器的均衡效果，m表示均衡器系数与信道系数的卷积，即实际均衡效果，mi(i∈[13,Lf])为m中不同TEQ长度下的值。

当mi=1时，对应的i值恰为TEQ长度范围的中值。其余i值下的mi都为0，说明均衡成功，并且SINR的值随Lf的增大而增大。否则，均衡效果不完善。

因此，本文依据信道系数托普利兹矩阵的条件数判断信道系数类型使用的求逆方法。通过改变信道系数的趋势，求得直接求逆、广义求逆下的信道系数托普利兹矩阵的条件数，并分析均衡成功或者失败时的条件数变化情况。首先，研究TEQ长度对SINR指标的影响；然后，通过对比直接求逆和广义求逆得到的SINR，评估两者适用的信道场景；最后，计算直接求逆和广义求逆得到的信道系数托普利兹矩阵的条件数，将条件数作为判断依据，判断哪类信道适用哪种求逆方法。

3 仿真结果与分析

实验中，采用MATLAB搭建无线通信环境下的迫零均衡仿真平台，分别选取凸峰形信道、信道系数趋势先下降后上升的信道以及信道系数趋势直接下降的信道进行仿真实验，研究信道系数的托普利兹矩阵的条件数与信道系数矩阵求逆方法的关系。

3.1 凸峰型信道的奇异矩阵问题

选取信道系数趋势先上升后下降的凸峰形信道，进行100组不同信道系数的测试。分别运用直接求逆和广义求逆方法求得均衡器的均衡系数，再将均衡器系数与信道系数卷积，得到均衡效果。选取其中一组数据的仿真结果进行展示，数据如下：

|hn|=[0.063,0.232,0.970,0.040,0.017,0.007]，|hh|=[0.096,0.365,0.903,0.096,0.157,0.091]

均衡效果如图1所示，均衡后的SINR与Lf的关系如图2所示。

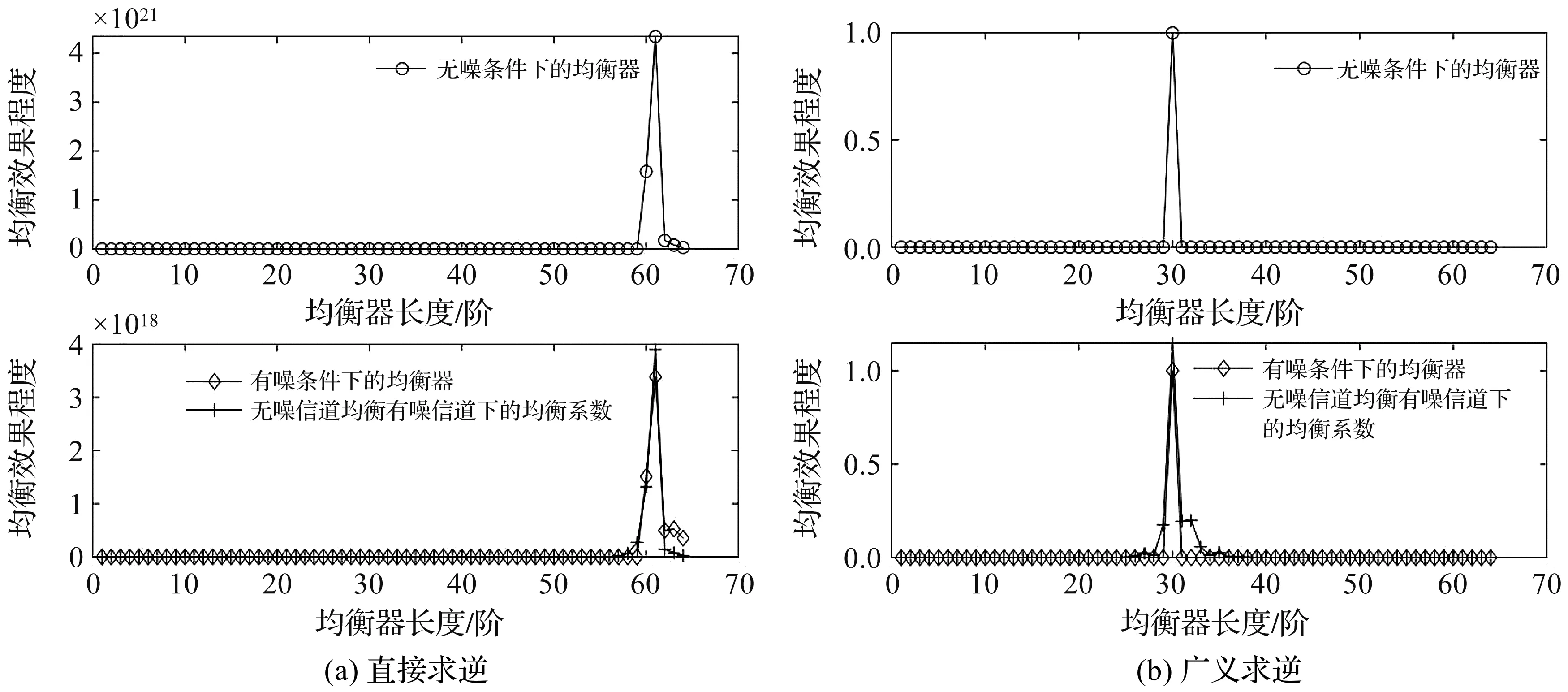
图1 凸峰型信道下，不同求逆方法的均衡效果

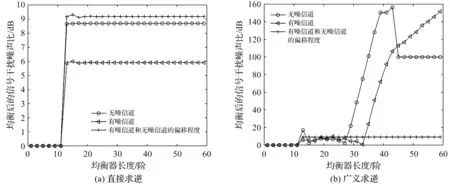
图2 凸峰型信道下，均衡后的SINR与Lf关系

从图1(a)中可以看出，均衡器长度在60位置时，均衡效果程度最大。而从图1(b)中可以看出，均衡器长度在30位置时，均衡效果程度最大。理论上来说，均衡效果最佳点对应的均衡器长度是TEQ长度范围的中值，因此，对于凸峰型信道来说，广义求逆的均衡效果更佳。

从图2可以看出，使用直接求逆方法均衡后，随着TEQ长度的增加，SINR陡然增加到一个常数，小幅波动后，趋于该常数。使用广义求逆方法均衡后，随着TEQ长度的增加，有噪信道下的SINR单调增大，而无噪声信道下的SINR突然下降到一个常数，这是因为在均衡器长度在(50，60)范围内，无噪信道的SINR远远大于有噪信道的SINR，为了更直观地观察无噪信道与有噪信道之间的变化，本文设定了一个限定值100 dB，即当SINR过大时，统一设为100 dB。

综上分析可以看出，直接求逆中，无噪信道、有噪信道以及信道偏移向量情况下的SINR是异常的。而广义求逆中，无噪信道和有噪信道情况下，SINR随着均衡器长度的增加而增大；信道偏移向量显示两者存在一定的偏移程度。因此，凸峰型信道中，广义求逆方法能改善凸峰型信道引发的奇异矩阵问题，均衡效果更佳。

3.2 广义求逆、直接求逆在各类信道系数趋势中的应用

分别采用直接求逆和广义求逆方法，计算信道系数托普利兹矩阵的条件数，分析2种求逆方法在信道系数呈正常指数下降、先下降后上升、先上升后下降这3种趋势下的均衡效果，通过条件数来判断采用哪种合适的求逆方法求得均衡器系数，对信道进行均衡。每类信道趋势进行100组信道实验。

3.2.1 正常指数下降的信道系数趋势

选取100组数据中的1组数据(|hn|=[0.992, 0.102, 0.067, 0.037, 0.003, 0.002]; |hh|=[0.909, 0.192, 0.110, 0.073, 0.307, 0.160])的实验结果进行展示，直接求逆和广义求逆下的均衡效果程度如图3所示。

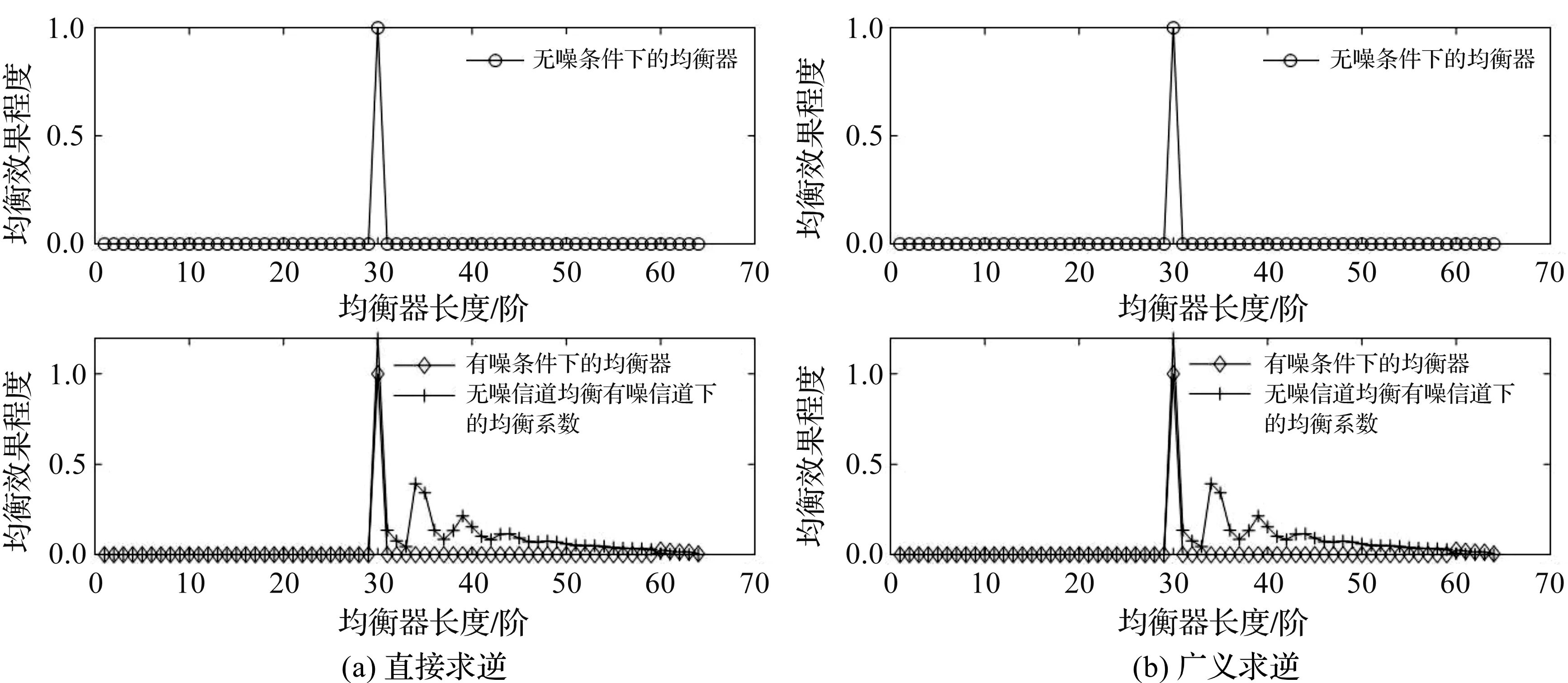
图3 信道系数呈正常指数下降趋势时，不同求逆方法的均衡效果

从图3可以看出，信道系数呈正常指数下降趋势时，直接求逆和广义求逆的均衡效果都不错。采用直接求逆和广义求逆方法得到的信道系数托普利兹矩阵的条件数如表1所示。

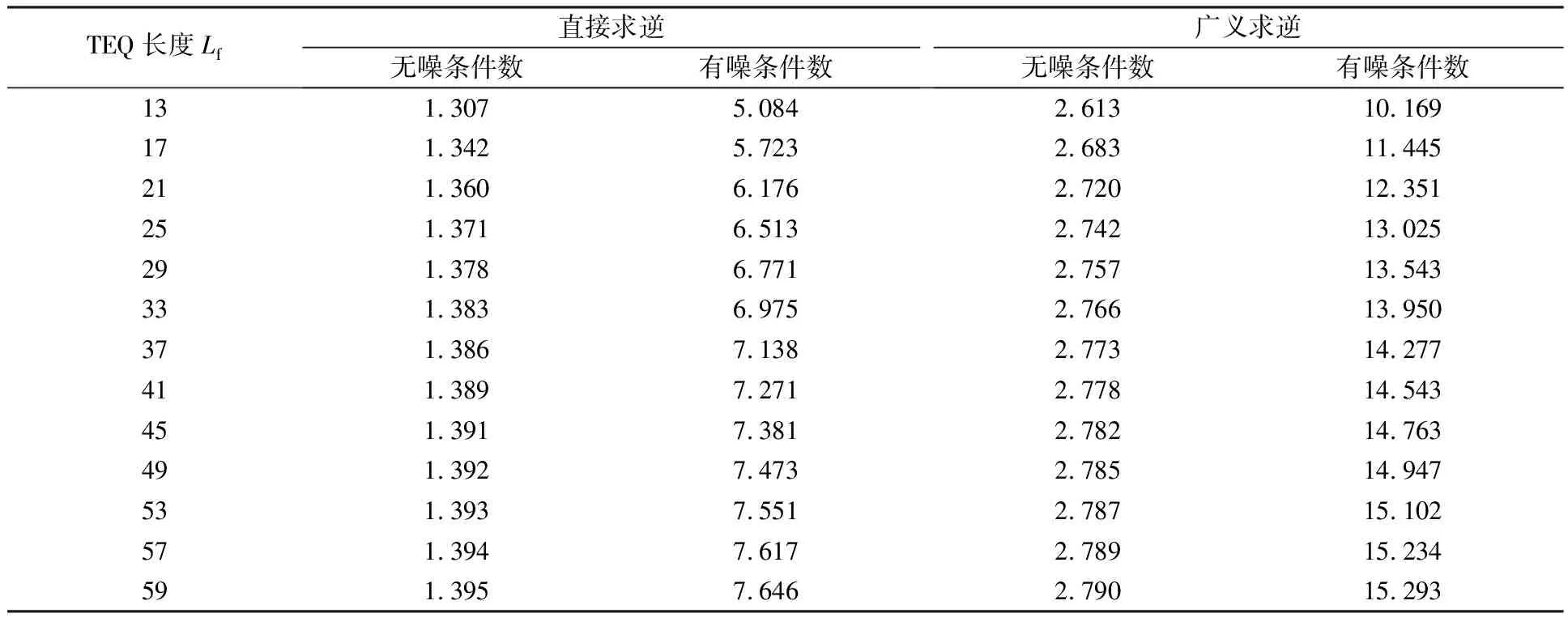
表1 信道系数呈正常指数下降趋势时，信道系数的托普利兹矩阵条件数

从表1可以看出，信道系数呈正常指数下降趋势时，不论是无噪条件还是有噪条件，广义求逆条件数大约是直接求逆条件数的2倍。

3.2.2 先下降后上升的信道系数趋势

选取其中一组数据(|hn|=[0.860, 0.482, 0.148, 0.005, 0.046, 0.070]; |hh|=[0.841, 0.360, 0.317, 0.200, 0.062, 0.141])的结果进行展示，直接求逆和广义求逆的均衡效果如图4所示。

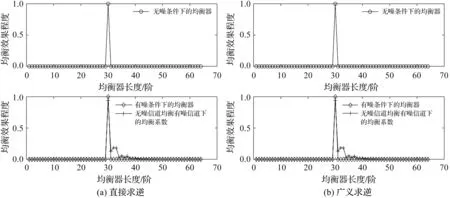
图4 信道系数呈先下降后上升趋势时，不同求逆方法的均衡效果

从图4可以看出，信道系数呈先下降后上升趋势时，直接求逆和广义求逆的均衡效果都不错。

采用直接求逆和广义求逆得到的信道系数托普利兹矩阵的条件数如表2所示。

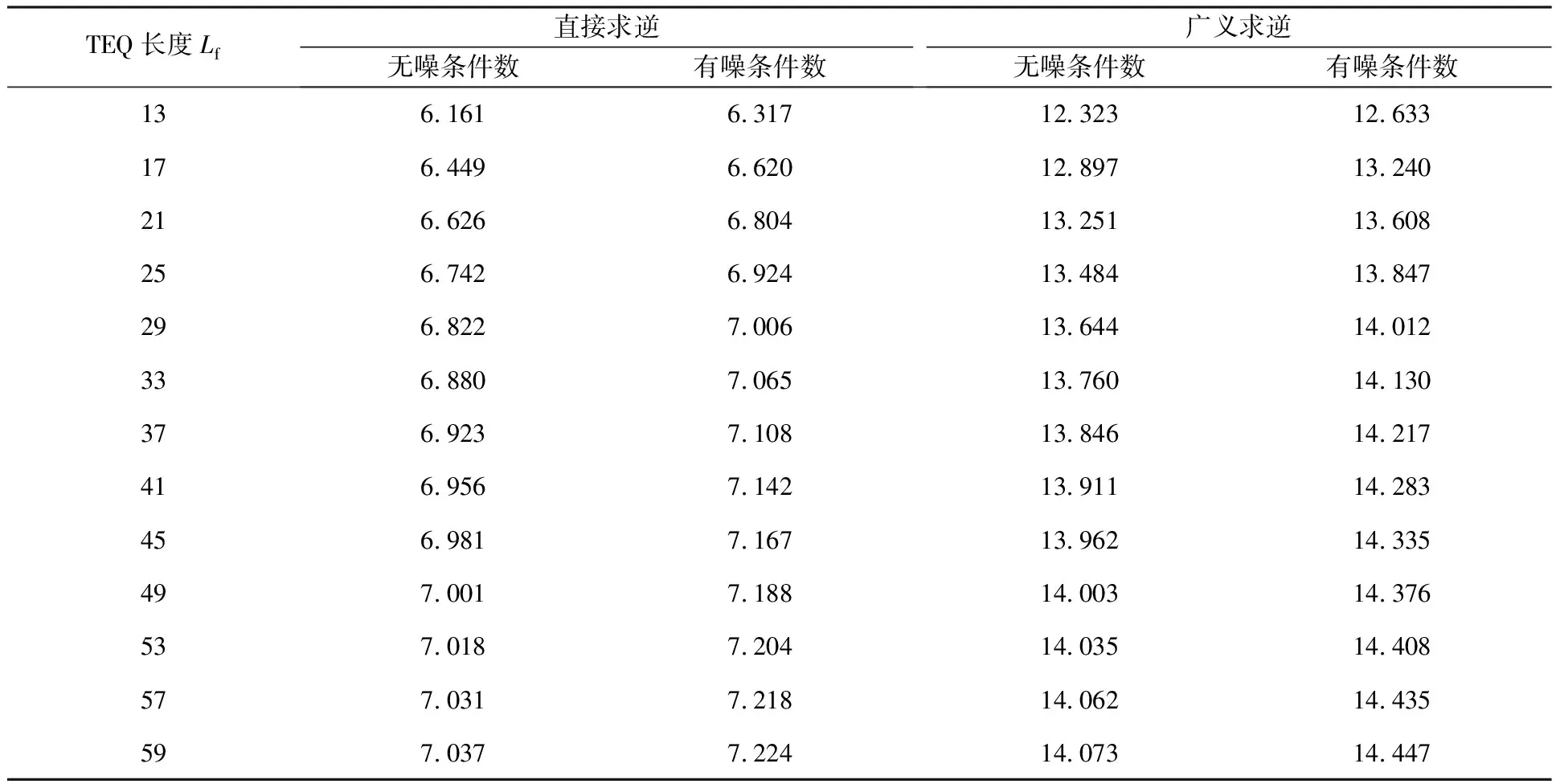
表2 信道系数趋势呈现先下降后上升情况下，信道系数的托普利兹的条件数

从表2可以看出，信道系数呈先下降后上升趋势时，不论是无噪条件还是有噪条件，广义求逆条件数大约是直接求逆条件数的2倍。

3.2.3 先上升后下降的信道系数趋势

选取其中一组数据(|hn|=[0.022, 0.160, 0.986, 0.034, 0.006, 0.005];|hh|=[0.176, 0.230, 0.914, 0.109, 0.077, 0.252])的结果进行展示，直接求逆和广义求逆的均衡效果如图5所示。

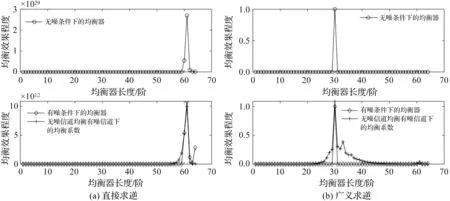
图5 不同求逆方法下的均衡效果图

由图5可以看出，信道系数呈先上升后下降趋势时，直接求逆的均衡效果异常，而广义求逆的均衡效果良好。

采用直接求逆和广义求逆得到的信道系数托普利兹矩阵的条件数如表3所示。

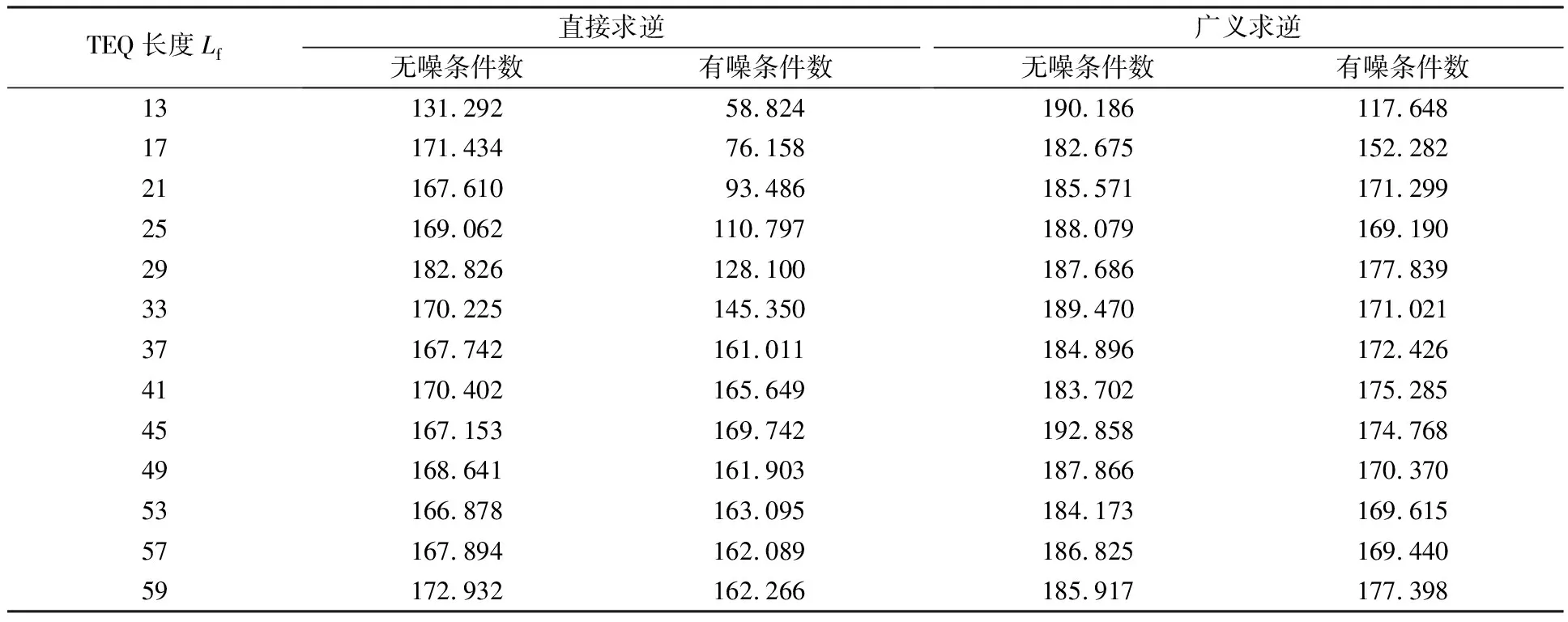
表3 信道系数趋势呈现先上升后下降情况下，信道系数的托普利兹矩阵的条件数

从表3可以看出，信道系数呈先上升后下降趋势时，不论是无噪条件还是有噪条件，随着均衡器长度的增加，广义求逆条件数与直接求逆条件数之间的差距在缩小。

综合以上分析可以发现，信道系数趋势呈正常指数下降或先下降后上升时，两者的条件数都小，皆可使用直接求逆或广义求逆方法；同时，两者的条件数均远小于凸峰型信道系统条件数；在凸峰型信道系统中，其条件数远远大于信道系数趋势呈正常指数下降或先下降后上升的条件数，使用广义求逆得到的均衡效果更佳。因此，在3类信道中，条件数较小时，可采用直接求逆和广义求逆方法来改进均衡；条件数较大时，则可采用广义求逆方法来改进均衡。