解三角形中的几类典型误区举隅

◇ 广东 陈 泳 闫 伟 罗辉芳

解三角形问题是历年高考的必考题，总体而言难度不大，但关于三角函数的定理、公式很多，利用正余弦定理和三角函数关系式解题时容易出现多解，学生往往缺乏相应的区分能力，所以“会而不对，对而不全”的现象常有发生．本文归纳了解三角形问题中几种常见的错误，以期帮助读者进一步提升对解三角形问题的认识，提高解题效率和准确性．

1 忽视余弦值为0

求解三角形问题时，大部分学生虽然掌握了相应解题方法，但没有严谨的解答过程，常常丢三落四而导致失分．例如，在等式两边消去相同因式——某个角的余弦，忘记讨论余弦值为0的情况，导致漏解．

例1在△ABC中，若sinC＋sin（B－A）＝2 sin2A，求角A．

错解sinC＋sin（B－A）＝sin（A＋B）＋sin（B－A）＝sinAcosB＋cosAsinB＋cosAsinB－sinAcosB＝2 cosAsinB＝2 sin2A，即cosAsinB＝sin2A＝2 sinAcosA，所以sinB＝2 sinA．

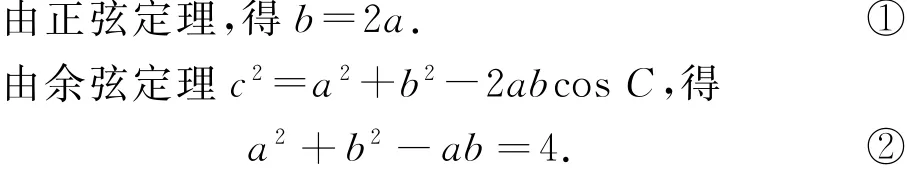
错误分析本题解答过程不严谨，等式cosA·sinB＝2 sinAcosA两边同时除以cosA时没有讨论cosA是否为0，当cosA＝0时，sinB＝2 sinA不一定成立．

正解解得cosAsinB＝sin2A＝2 sinAcosA，所以（sinB－2 sinA）cosA＝0．当cosA＝0时，

当sinB＝2 sinA时，由正弦定理，得

由余弦定理c2＝a2＋b2－2abcosC，得

点评

学生考试估分和实际得分相去甚远，很多时候都是没有养成规范的答题习惯所引起的．在求解三角形问题时，等式两边都有相同未知数要特别注意，如果等式两边都有相同角的余弦则不能随便约去，例题中的错误就是由随便消元造成的．针对这种情况，我们可以先移项然后提公因式，避免漏解．总之，学好数学需要细心，不能急功近利，要重视解题的规范性训练，努力做到“会又对、对又全、全又美”．

2 忽视三角形内角的范围

1）角的范围缩小

例2（人教A版《必修5》课后题）在△ABC中，已知sin2A＝sin2B，试判断△ABC的形状．

错解因为sin2A＝sin2B，所以2A＝2B，A＝B，△ABC为等腰三角形．

错误分析sin2A＝sin2B与2A＝2B不是等价的，没有考虑三角形中角的范围，从而导致错误．

正解因为A，B∈（0，π），所以2A，2B∈（0，2 π）．因为sin2A＝sin2B，所以2A＝2B或2A＋2B＝π，即A＝B或，故△ABC为等腰或直角三角形．

2）角的范围扩大

例3在△ABC中，求cosC．

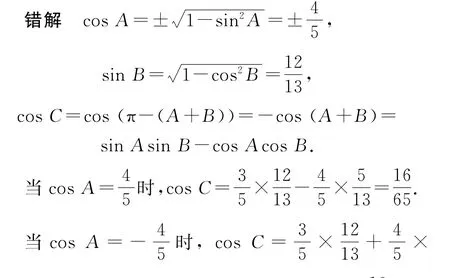
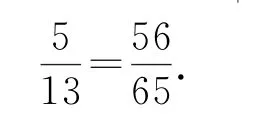
错误分析忽略了角A的取值范围，在△ABC中，sinB＞sinA是B＞A的充要条件，而角B为锐角，则A必为锐角．

正解，所以sinB＞sinA，所以B＞A，则A为锐角，故

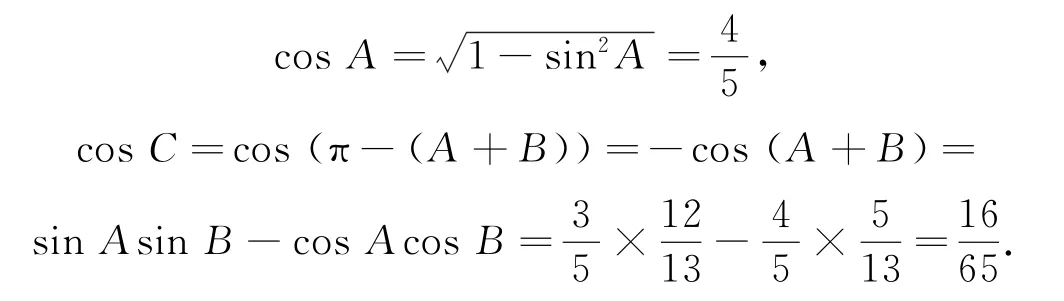
例4（2019年全国卷Ⅲ）△ABC的内角A，B，C的对应边分别为a，b，c．已知

（1）求B；

（2）若△ABC为锐角三角形且c＝1，求△ABC面积的取值范围．

因为△ABC为锐角三角形，所以，所以tanC∈（0，＋∞），则，所以

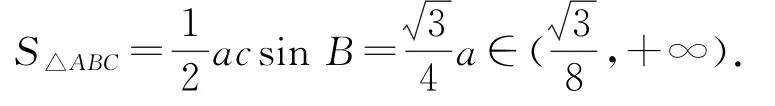
错误分析学生虽然能够注意到△ABC是锐角三角形这一条件，但没有注意到已知一个角的度数，则另外两个角之和就为定值．若仅注意到另外两个角各为锐角这一条件，就会把角的范围扩大导致出错．

正解（2）同上可知所以，所以，则a∈，所以

例5在锐角△ABC中，a＝1，B＝2A，求b的取值范围．

错解1由正弦定理，可得

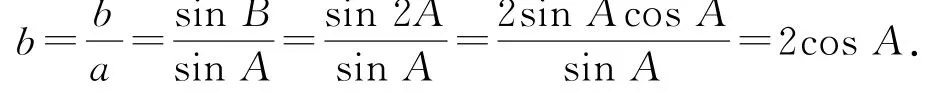
错解2因为，所以，所以，则，所以

错解3因为，所以则，所以

错误分析学生在利用正弦定理化简得到2 cosA后，主要存在着以下几种易错点．错解1:没有考虑到角B的范围限制，从而将角A的范围扩大了；错解2:利用了B＝2A且B是锐角这一条件求出了角A的范围，但没有考虑到三角形内角和为180°，角C的范围也制约着角A的范围；错解3:考虑到角C的范围会影响角A的范围，但没有考虑到角B的范围，导致角A的范围扩大了．以上3种是常见的易错点．除此以外还有一些基本功不过关的常见错误，如求出了角A的范围，但是cosA的大小范围写错了，误认为A＝2B和sinA＝2 sinB是等价的．

点评

求三角形内角的范围是解三角形中的一个难点，对学生思维的严谨性、完备性要求较高．角的取值范围一般隐含在题目的条件中，若不仔细审题、深入挖掘，往往会因为疏漏而导致解题错误，解题时可以从以下几个方面入手．

1）认真审题捕捉锐角、钝角等“题眼”，注意挖掘隐含在题中的相关信息，例如某个角的余弦值为负数，说明这个角为钝角；三角形的三个内角中最多只有一个钝角；大边对大角求得小边所对的角一定为锐角等．

2）在任意三角形中，三个内角之和等于180°，所以才会有三个内角均介于0°～180°之间这样的隐含信息，解题时要注意深挖题目的隐含信息，明确几个内角间的大小关系．

3）在研究钝角三角形的内角大小时要分类讨论，做到不重不漏、有理有据．

4）如果已知三角形的某一个内角，那么余下的两个角之和必为定值，这就形成了一种制约关系，利用这个关系可以总结一些相关结论:1）锐角△ABC中最大内角的范围是[60°，90°），最小内角的范围是（0°，60°]；2）锐角△ABC中，若A＝30°，则B，C∈（60°，90°）；若A＝60°，则B，C∈（30°，90°）；3）锐角△ABC中的任意两角之和必大于90°等．

3 忽视三角形边的范围

例6在△ABC中，已知2，则B＝________．

错解由正弦定理，得，所以B＝30°或150°．

错误分析忽视了边a和边b的大小关系，从而忽视了角B也有大小范围的限制．

正解由正弦定理，得，因为a＞b，所以A＞B，则B＝30°．

点评

若已知两边及其对角时，运用正弦定理解得另外一角的正弦值会有两种答案，要根据大边对大角的情况，对角的解进行分析．

例7已知2a＋1，a，2a－1为钝角三角形的三条边，求a的范围．

错解1设最大边2a＋1所对的角为θ，则θ为钝角，所以

当2a（2a－1）＞0，即a＜0或时，a2＋（2a－1）2－（2a＋1）2＜0，解得0＜a＜8，故

当2a（2a－1）＜0，即时，a2＋（2a－1）2－（2a＋1）2＞0，解得a＜0或a＞8，无解．

错解2由题意得所以．设2a＋1为最大边，其所对的角为θ，则θ为钝角，所以，解得0＜a＜8，所以

错误分析错解1忽视了三角形的三边长均大于0，而且错解1和错解2都只考虑了最大边所对的角为钝角，忽视了“三角形中两边之和大于第三边”的隐含条件．

正解由错解2，得又因为三角形三边满足a＋（2a－1）＞2a＋1，所以a＞2，于是2＜a＜8．

点评

三角形的三边需满足每条边都为正数，且任意两边之和大于第三边，两边之差小于第三边．

例8（2013年北京卷）△ABC中，a＝3，b＝2，B＝2A．

（1）求cosA的值；

（2）求c的值．

错解（求解过程略）．

错误分析忽视了c的取值范围，所以，故A，B为锐角，所以sinC＝sin（A＋B）＝sinAcosB＋cosA·sinB＞cosAsinB，所以c＞bcosA＝4．

正解解得c＝3或5，又cosB＝cos2A＝，故B为锐角，当c＝3时，b2＞a2＋c2，B为钝角，舍去，所以c＝5．

点评

在使用余弦定理求出某条边有两个值时要注意值是否满足条件，例如，已知a，b，cosA，求出c有两个值，就要利用正弦、余弦定理验证另外一个角B或C的值是否满足条件．

在解三角形问题中，经常会出现多解现象，稍不注意计算就会出错．俗话说，“失败是成功之母”．解三角形问题涉及的公式多，对学生的思维能力、运算能力要求较高．做错题是再平常不过的，教师要引导学生关注细节，多总结分析，弄清楚在哪一个知识点、哪一个方法、哪一个环节上出现了问题，把错题归类，日积月累，才能在解题时融会贯通、游刃有余．