一题多变，玩转解三角形最值问题

◇ 山东 高 磊

秉纲而目自张，执本而末自从．高三复习阶段，学生要做的习题浩如烟海，为了摆脱题海战术，就需要学生通过一题多变、一题多解、多题归一的训练开展深度学习；通过改变条件、整合知识，找到规律，一通百通．在数学教学中，教师需通过一题多变培养学生的发散思维；通过多题归一，培养学生收敛思维．笔者依据多年高三教学经验，认为散敛思维应有中心、有目标、可迁移，做到周密、有效．现结合解三角形内容谈谈个人观点．

1 题根研究

题根（2020年全国卷Ⅱ理科第17题）△ABC中，sin2A－sin2B－sin2C＝sinBsinC．

（1）求A；

（2）若BC＝3，求△ABC周长的最大值．

解法1（1）由正弦定理和已知条件，得

由余弦定理，得

因为0＜A＜π，所以

（2）由正弦定理及（1），得

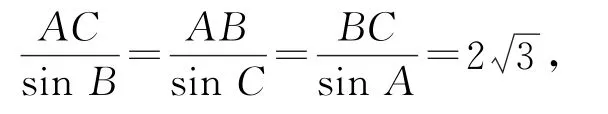
故

解法2（1）同解法1．

（2）设△ABC的内角A，B，C所对的边分别为a，b，c，由余弦定理，得

又因为a＝3，所以所以（b＋c）2≤12，所以，当且仅当b＝c＝时，等号成立．因为a＝3，所以故△ABC周长取得最大值

点评

本题考查了解三角形的相关知识，涉及正弦定理角化边的应用、余弦定理的应用、三角形周长最大值的求解等．

2 变式训练

变式1在△ABC中，若，求△ABC面积的最大值．

基于这个考点，进行如下变式训练，引领学生全面掌握解三角形中的最值问题．

解析

在△ABC中，由基本不等式，可得a＋c≥当且仅当a＝c时，等号成立．

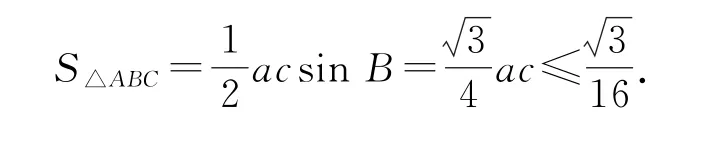
点评

变式2在△ABC中，若，求△ABC周长的取值范围．

解析

在△ABC中，由余弦定理，得b2＝a2＋c2－2accosB＝（a＋c）2－3ac＝1－3ac．由基本不等式，得当且仅当a＝c时，等号成立．所以

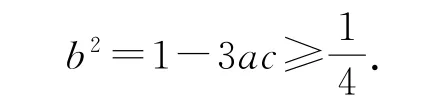
又因为0＜b＜a＋c，所以，所以a＋b＋c＜2，故△ABC周长的取值范围为

点评

根据余弦定理和基本不等式可以推导出b≥，再结合三角形两边之和大于第三边得出周长的取值范围．

变式3在△ABC中，若，求△ABC周长的取值范围．

解析

在△ABC中，由余弦定理，得

又因为b＝1，a＋c＞b，所以1＜a＋c≤2，所以2＜a＋b＋c≤3，故△ABC周长的取值范围为（2，3]．

点评

由余弦定理和基本不等式相结合可以推导出a＋c≤2，再结合三角形两边之和大于第三边得出周长的取值范围．

变式4若△ABC为锐角三角形求△ABC周长的取值范围．

解析

由正弦定理，得

所以

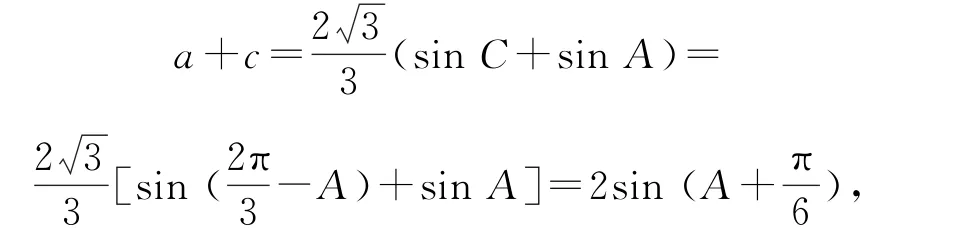
因为△ABC为锐角三角形，所以解得，所以，所以a＋c＝，故

点评

与变式3相比，会发现在锐角三角形中，利用基本不等式无法使问题获解．本题运用正弦定理得出，此为正弦型函数，再利用锐角三角形这一条件进一步缩小角A的范围，求出周长的取值范围．

变式5在△ABC中，若，求△ABC的面积的最大值．

解析

在△ABC中，由余弦定理，得

由基本不等式，得a2＋c2≥2ac，b2＝a2＋c2－ac≥ac，所以ac≤1，当且仅当a＝c时，等号成立．所以

点评

本题运用余弦定理和基本不等式求解三角形面积最大值．

变式6在△ABC中，若，求△ABC面积的取值范围．

解析

由正弦定理，得

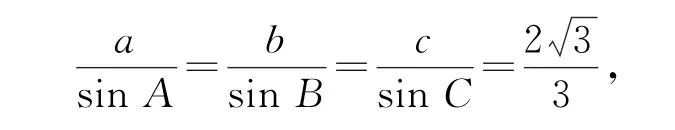
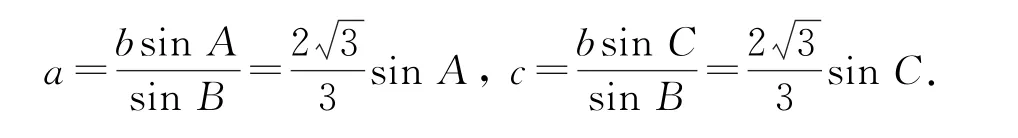
所以

所以

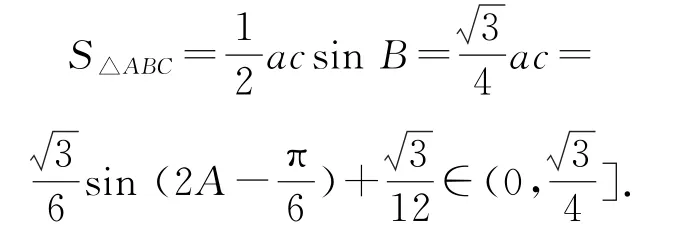
点评

本题运用正弦定理、和角公式、倍角公式、辅助角公式等求解面积的取值范围．

变式7若△ABC为锐角三角形求△ABC面积的取值范围．

解析

因为△ABC为锐角三角形，所以

点评

运用“锐角三角形”这一条件缩小角A的范围是本题的易错点．

变式8在△ABC中，，若D为边AC的中点，且BD＝1，求△ABC面积的最大值．

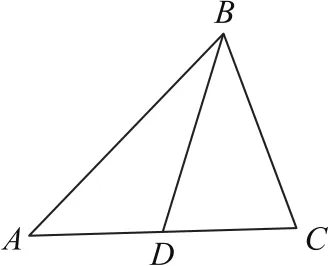
图1

解析

因为BD为边AC的中线，所以，则

由基本不等式，得4＝c2＋a2＋ac≥3ac，所以，当且仅当a＝c时，等号成立．

点评

当中线为定值时，在△ABC中运用建立方程，再运用基本不等式求出ac的最大值，从而求得面积的最大值．

变式9在△ABC中，若BD为∠ABC的角平分线，且BD＝1，求△ABC面积的最小值．

解析

因为BD为∠ABC的角平分线，且BD＝1，

由S△A B C＝S△A B D＋S△B C D，得

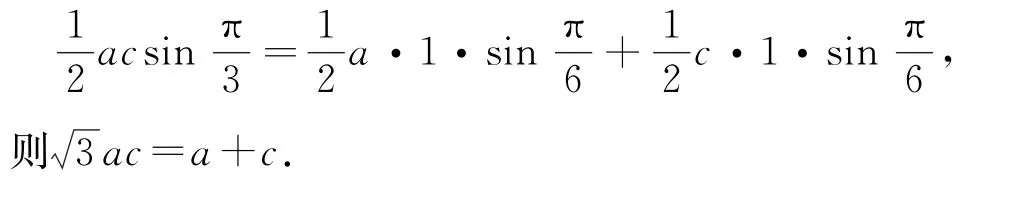
点评

当角平分线为定值时，可运用面积关系S△A B C＝S△A B D＋S△B C D建立方程，再运用基本不等式求出ac的最小值，从而求得面积的最小值．

变式10在△ABC中，，若BD为边AC上的高，且BD＝1，求△ABC面积的最小值．

解析

在△ABC中，因为BD为边AC的高，且，所以

由余弦定理，得b2＝a2＋c2－2accosB＝a2＋c2－ac，所以，由基本不等式，知a2＋c2≥2ac，得所以ac≥，当且仅当a＝c时，等号成立．所以

△ABC面积的最小值为

点评

一题多变是对一道题目进行变式研究，采取分层次多视角的剖析，通过题设、结论的变化及引申新问题让学生对知识的理解更深刻，能够帮助学生加深对基础知识和基本技巧的掌握，激发学生解题和钻研的欲望，提升学生触类旁通、纲举目张、举一反三的能力．一题多变也是创造性思维的体现，对培养学生思维的广阔性、探索性、深刻性、独创性、灵活性都是非常有效的途径．在高三复习中，灵活运用一题多变能够收到“讲好一题，带活一片”的效果．