反手性蜂窝橡胶覆盖层面内冲击动力学分析
2020-11-23李俊杰
李俊杰,陶 猛
(贵州大学机械工程学院,贵州 贵阳 550025)
1 引言
舰船作为重要的海上战斗力已成为各国军事发展的主要组成,随着现代武器科技的发展,对舰船的抗冲击能力以及反探测隐身能力提出了更高的要求[1]。敷设于舰船壳体湿表面的超弹性橡胶覆盖层已被证明能有效减振吸声降噪的同时为船体受冲击提供良好的防护途径。空腔覆盖层能有效抑制水中声辐射,特别是对低频段噪声的抑制作用显著[2]。空腔形式亦对吸声性能有较大影响,不同大小的空腔嵌入改变吸声覆盖层声学特性的规律[3],其中手性蜂窝填充的空腔覆盖层中波形转换过程被证明能有效消除声辐射[4]。为实现覆盖层的隔声和抗冲击双重能效,对空腔覆盖层的抗冲击性能研究已大量展开。文献[5]通过试验研究了橡胶夹芯覆盖层对船体受水下爆炸时的防护作用,研究表明流固耦合作用使覆盖层接收的入射冲量大幅减少且覆盖层有效降低了整体结构受爆炸冲击的响应峰值。文献[6-7]研究了手性蜂窝橡胶覆盖层水下爆炸响应并发现覆盖层抗冲击性能随着其镂空率、高度和基体材料波阻抗的增加而得到提高。另外,对超弹性橡胶材料分层圆孔蜂窝覆盖层动态压缩行为进行研究,发现芯层排布形式影响结构压缩性能。文献[8]对超弹性覆盖层单胞模型受冲击作用下的波传递和缓冲特性进行研究,发现胞元抗屈曲性能能够提升结构的缓冲作用。目前,覆盖层的抗冲击性能研究主要集中在简单圆孔空腔形式,而手性形式研究较少。具备独特力学性能优势的负泊松比多孔材料已受到广泛关注[9-12]。反手性蜂窝具有基于旋转机制的负泊松比特性[11],同时韧带缠绕特征导致的纵波、横波和扭转波的波形变换特性对能量衰减显著,将其作为填充芯层的超弹性橡胶覆盖层兼具抗冲和隔声潜力。
反手性蜂窝作为填充芯层时,不可避免的受到各种外力冲击。当考虑惯性效应且蜂窝材料非线性时,反手性蜂窝在不同速度冲击下的面内宏观响应以及与胞元结构的关系显得尤为重要。对于反手性蜂窝作为填充芯层的超弹性橡胶覆盖层面内冲击性能与胞元结构的关系尚不明确。以四韧带反手性蜂窝为例,分析反手性蜂窝橡胶覆盖层受面内冲击作用下的变形特征并具体讨论壁厚不同的反手性蜂窝橡胶覆盖层受面内冲击作用下的动力学响应和能量吸收能力,以期建立覆盖层宏观力学性能与反手性胞元结构的关系。
2 模型的建立
2.1 四韧带反手性蜂窝几何结构
四韧带反手性蜂窝的几何结构参数,其中r、l、t 分别为外圆环半径、相邻圆环节点间距离和韧带壁厚,如图1 所示。这里为保持覆盖层等体积且填充胞元排布一致,保持外圆环半径和节点间距离不变,取 r=3.5mm、l=9mm,壁厚t 取(1.5~2)mm。
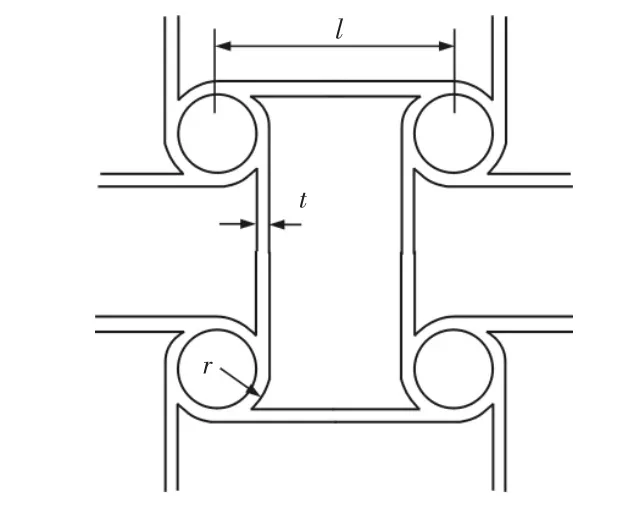
图1 四韧带反手性蜂窝胞元几何参数Fig.1 Diagram of Anti-Tetrachiral Cell Showing Geometric Parameters
2.2 计算模型
利用非线性显示动力学软件ABAQUS/Explicit 对反手性蜂窝橡胶覆盖层面内冲击特性进行数值分析。对应计算模型,如图2 所示。这里为避免面板材料的影响,覆盖层上下面板均采用2mm 厚橡胶。冲击端和固定端为解析刚体。刚体采用刚性连接单元离散,覆盖层采用平面应力单元离散,为保证应力应变在胞元转角处等大变形区域的收敛,网格尺寸选为0.5mm。刚性板与覆盖层上、下表面采用面-面接触算法,摩擦因数取0.2。覆盖层内部各胞壁均定义自接触属性,以防止橡胶材料大变形计算过程中出现穿透现象。为保证覆盖层不被压缩至完全密实化,选择总高度的60%作为y 方向压缩应变量。
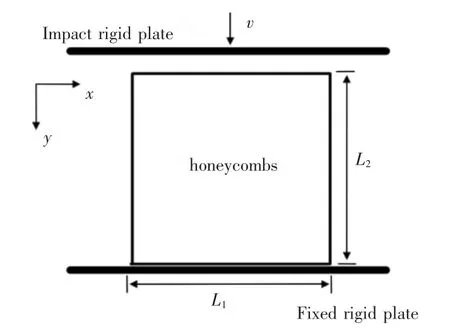
图2 覆盖层面内冲击加载示意图Fig.2 Diagrammatic Sketch for the Claddings Under In-Plane Impacting
四韧带反手性蜂窝覆盖层相对密度可由胞元承载面积与覆盖层总体横截面积比值得出,其相对密度由下式给出:

式中:ρ*—四韧带反手性蜂窝材料密度;ρs—橡胶材料密度;li,ti—第i 个胞元韧带长度和对应壁厚;L1、L2—覆盖层宽度和高度。根据式(1),不同壁厚的反手性蜂窝覆盖层结构特征参数,如表1 所示。

表1 蜂窝覆盖层特征参数Tab.1 Characteristic Parameters for Honeycomb Claddings
2.3 橡胶材料试验数据及拟合
橡胶为各向同性、几乎不可压缩材料,应力应变关系高度非线性。超弹性材料本构关系复杂,需要选用合适的本构方程以获得更为准确的应力应变关系。通过试验机测得的一组邵氏硬度60(Shore60)氯丁橡胶材料试验数据[5]和不同本构模型拟合结果,如图 3 所示。这里选择 Arruda-Boyce、Ogden_N2、Mooney-Rivlin、Neo Hooke 和Yeoh 五组常用超弹性本构模型对单轴拉压试验数据进行拟合。小应变区间里几种拟合结果均符合试验值。应变达到 200%时,Mooney-Rivlin、Neo Hooke 和 Yeoh 拟合值与试验值曲线分离。同时在整个应变范围内,Arruda-Boyce 更加接近试验值。综合几种本构方程对试验数据拟合结果同时考虑覆盖层受冲击后的大变形特性,选用更能准确模拟大应变区间材料特性的Arruda-Boyce 模型。材料参数 μ=0.794955818、λ=3.02114397、D=0,单位均为 MPa。

图3 不同本构模型拟合结果Fig.3 Fitting Results of Different Constitutive Models
3 结果讨论与分析
主要考察反手性蜂窝橡胶覆盖层在不同冲击速度下的变形特征。分析动力学响应和能量吸收规律与覆盖层宏观变形的关系,具体讨论等体积、胞元排布一致但壁厚不同的覆盖层冲击端压力、底端支反力响应和能量吸收能力。
3.1 反手性蜂窝覆盖层动态响应
在面内冲击作用下,局部胞元变形和整体变形模式是反手性蜂窝动态响应的典型特征。壁厚t=1.5mm 的反手性蜂窝覆盖层在不同冲击速度下的瞬态响应及变形过程,如图4 所示。在1m/s的准静态冲击下,压缩应力波自上而下逐层传递,过程伴随胞元的微弱变形。在应变ε=0.1 时,整体响应均匀,反手性韧带缠绕的变形机制导致左右两侧向内颈缩,表现出旋转机制的负泊松比特性。随着应变加大,颈缩接触的胞壁开始屈曲,圆孔交替顺时针和反时针的扭转变形。在应变ε=0.4 时,胞元被分层压溃,出现不对称的垮塌。之后进入密实化阶段。随着冲击速度的增加(v=5m/s),在较小应变(ε=0.1)里,胞元屈曲变形。随着向下的压缩,所有胞元韧带呈现无序的扭转变形。在应变ε=0.4 左右,缠绕变形模式导致左右两侧向内收缩,呈现出“><”形,表现出负泊松比特性。随着冲击速度的进一步增加(v=15m/s),惯性效应显著,变形集中在冲击端,胞元被逐层压垮闭合,胞元旋转和韧带缠绕大幅减弱,呈现出传统蜂窝材料的“I”形坍塌模式。

图4 不同冲击速度下反手性蜂窝覆盖层的瞬态响应Fig.4 The Response of Anti-Tetrachiral Honeycomb Claddings Under Different Impact Velocities
3.2 动力学特性
通过提取冲击刚性板压力,反映覆盖层达到对应应变时所承载力的作用。固定刚性板支撑反力,间接反映船壳体受力。不同冲击速度下不同壁厚的反手性蜂窝覆盖层的冲击端压力和底端支反力与压缩应变的关系曲线,如图5 所示。
在1m/s 的准静态冲击下,冲击端压力曲线整体趋势随压缩应变的增大而逐渐增大。蜂窝孔壁产生线弹性弯曲,在此线弹性压缩阶段,应力与应变呈线性增大的关系。覆盖层整体响应均匀,支反力曲线与冲击端压力相似。随着冲击速度的增大(v=5m/s),冲击端初始压力明显提高,向下压缩初期孔壁逐层屈曲再恢复变形,压力曲线往复震荡。应变ε=0.3 左右,覆盖层胞元进入整体无序扭转变形阶段,向内收缩的变形引起整体刚度的增加,压力快速上升。之后逐层的垮塌引起压力上升过程中的震荡。在应变到达ε=0.17 左右时支反力由零开始增长,且较准静态下的增长速率更快。对比曲线震荡上升过程,压力波峰(ε=0.33、ε=0.48 和ε=0.58)正是支反力波谷,两次波谷(ε=0.42 和ε=0.55)对应支反力波峰,这与覆盖层的垮塌变形模式相对应。随着冲击速度的进一步增大(v=15m/s),冲击端初始压力显著提高,逐层压垮的变形模式形成冲击端的应力平台期。在ε=0.55 左右,进入密实化阶段,冲击端压力陡升。响应前期底端不受压力载荷,底端响应远滞后于冲击端响应,压缩波传到底端边界前,支反力为零。在应变到达ε=0.35 附近时,支反力出现陡升,随即迎来峰值。在各冲击速度下,相同名义应变内冲击端压力和底端支反力均随壁厚增大而增大。

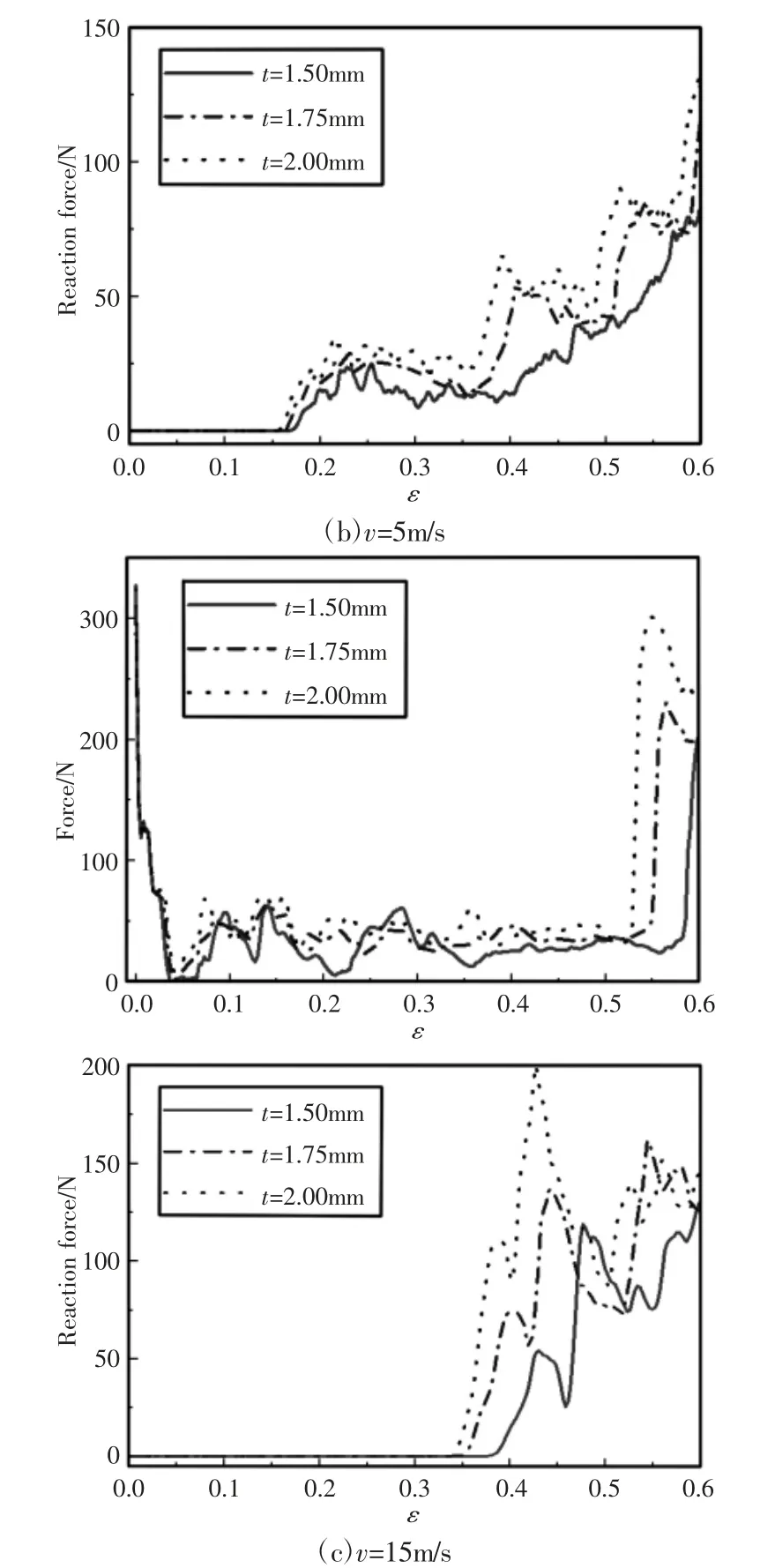
图5 不同冲击速度下覆盖层冲击端压力和支反力-应变曲线Fig.5 Force and Reaction Force-Stain Curves of Claddings Under Different Impact Velocitie
3.3 能量吸收性能
反手性蜂窝橡胶覆盖层压缩运动产生动能和结构变形储能为最主要能量吸收形式。这里将动能与应变能之和作为覆盖层总吸收能量。比吸能(即质量能量吸收率)为评估多胞结构能量吸收能力重要指标[13]:

式中:Wv—单位体积吸收能量¯—覆盖层相对密度;ρs—橡胶材料密度。据此可得不同冲击速度下,相同体积相同胞元排布方式但不同壁厚的覆盖层的比吸能与压缩应变的关系,如图6 所示。
总体上看出,同一冲击速度下,随着壁厚的增加,反手性蜂窝覆盖层比吸能增加;对同一壁厚的覆盖层,随冲击速度的增加,比吸能增加。在准静态过程中(v=1m/s),应变ε=0.2 之前,不同壁厚覆盖层比吸能相近。应变ε=0.2 之后,胞元壁厚差异引起屈曲变形难度不一样,比吸能曲线分离。随着冲击速度的增大(v=5m/s),应变达到ε=0.3 之后的无序垮塌过程中各覆盖层比吸能曲线分离。随着冲击速度的进一步增大(v=15m/s),逐层压垮的变形模式导致比吸能曲线在很小应变时分离。各冲击速度下,覆盖层比吸能均随胞元壁厚增大而增大。一方面,壁厚越大胞壁更早的接触靠拢,旋转变形机制使得更不易变形;另一方面,壁厚越大覆盖层相对密度越大,继而率先进入密实化阶段。

图6 不同冲击速度下覆盖层能量吸收Fig.6 Energy Absorption of Claddings Under Different Impact Velocities
4 结论
基于显示动力学有限元方法,对具有负泊松比特性的反手性蜂窝胞元填充的橡胶覆盖层的冲击动力学进行数值分析。结果表明:(1)冲击速度影响反手性蜂窝橡胶材料变形模式。在中低速下,结构两侧呈现向内收缩变形,旋转机制的负泊松比特性突出。随速度增加,惯性效应显著,变形集中在冲击端。(2)覆盖层冲击端压力和支反力响应与覆盖层变形过程存在对应关系。随冲击速度增大,冲击端压力和底端支反力增大。同一速度下,壁厚越大的覆盖层冲击端压力和支反力均越大。(3)随冲击速度增大,各覆盖层表现出更强的能量吸收能力。在冲击速度和名义应变一定的条件下,壁厚越大的覆盖层能量吸收能力越高。
