基于有限元的PFWD机场土面区检测过程模拟可行性分析
2020-11-19江圣泽方学东高建勇汪家浩蒙花杏
江圣泽,方学东,高建勇,汪家浩,蒙花杏
(1.中国民航飞行学院,四川 广汉618307;2.南京工业大学 交通运输工程学院,江苏 南京210009)
当飞机由于意外状况冲出跑道时,主起落架会对升降带土体产生一定的冲击作用。2020年6月,某航空公司运输机在机场着陆时冲出跑道,受降雨影响,升降带土壤含水量增加,导致飞机的主起落架陷入土中。机场升降带土面区是用以减少飞机冲出跑道时遭受损坏危险的区域,为保证土体的承载力,机场每年都需遵照相关要求进行土质地带的密实度检测试验。现有的传统检测方法,从取土至击实并得出最后结果需要耗费大量时间,段丹军等采用PFWD建立了以红黏土为填筑路基的压实度与PFWD所测得的动弹性模量的关系曲线,这种模型适用于路基压实强度的快速评价[1]。为了提高对机场土质区密实度的检测效率,减少人工取土开挖的巨大工作量,可采用PFWD对密实度进行评价的方法。由于机场土质区的设计、施工、维护要求与民用公路不同,因此,有必要对PFWD在土面区的检测过程进行模拟,验证检测方法的合理性。
1 测试模拟方案
1.1 PFWD测试原理
PFWD——便携式落锤弯沉仪是一种基础填筑表面(包括路基、地基和场地平整)动力承载能力试验检测设备,是继常规拖车式落锤弯沉仪(FWD)后的又一种新的动力模量快速无损检测设备[2]。其基本原理为向一定高度提升10kg落锤,随后自由下落[3],落锤对土体表面产生冲击,导致土体在冲击荷载作用下产生位移。此时,仪器底端的感应装置受到冲击后能够根据式(1)自动计算出土体的回弹模量。
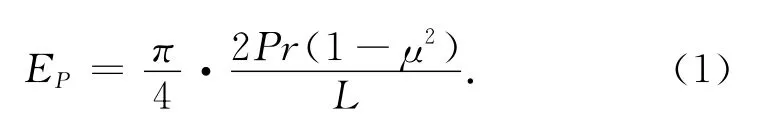
式中:EP为土质区填土动弹性模量,MPa;P为承载板所受最大压应力,kPa;r为承载板半径,mm;μ为土体泊松比;L为承载板中心弯沉值,μm。
与普通公路填土路基不同,由于土面区需要进行保护,机场升降带应覆盖植被。部分机场为保障航班的安全运行,甚至还种植芍药以达到驱鸟的目的(见图1),所以在进 行PFWD测试时应当尽可能减少对植被的影响。

图1 某机场升降带植被
使用环刀法、灌砂法、灌水法等传统方法测试时,应先去除表层植被,再开挖土体至表层深度30 cm位置时取样试验。使用PFWD在机场土面区检测时,不需要对土样进行开挖,只需使土面露出与承载板面积相应的区域便可操作实验,如图2所示。

图2 PFWD——便携式落锤弯沉仪机场土面区测试
1.2 测点布置
机场飞行区合理的植被建设,既能有效预防水土流失,美化机场环境,又能对鸟害防治发挥积极作用,对保障飞行安全具有重要意义[4]。使用PFWD进行检测时可以按照《民用机场飞行区场地维护技术指南》进行测点布置[5]。同一密实度测试区域内的测试点不得少于3个,与跑道道肩的距离宜小于75m。测试点之间的距离不得小于50m,各测试点检测数量不得少于3组,每组间隔不少于2m。检测时只需将仪器放置于土体表面,不需要开挖土样。具体测点布置如图3所示。

图3 PFWD土质区测点分布
检测前应将各个检测组进行编号,且号码必须唯一。编号宜采用分段形式,各字段应有明确意义。如图1中,“s1-r-2-1”中,“s1”表示升降带第一个取样区,“r”表示跑道右侧,“2”表示第一取样区中的第二组,“1”表示第二组中的第一个点;“a1-f-1-1”中,“a1”表示跑道端安全区中第一个取样区,“f”表示跑道前端的安全区(后端用“b”表示),“1”表示跑道端安全区第一个取样区,“2”表示第一个取样区中第二个点。
2 土面区三维有限元模型建立
2.1 机场土质区土样物理参数
周文曾使用ABAQUS软件对PFWD在路基方面的测试工作进行仿真模拟[6],为了进一步研究便携式落锤弯沉仪在机场密实度检测过程中的适用性,根据测试原理,利用某机场土面区填土各土层物理力学性质指标,采用有限元软件建立三维模型,模拟仪器在测点检测时落锤锤击承载板时土体产生的作用,观察应力影响深度与位移变形范围。
土质区上部的素填土为黏性土,颜色为灰-灰黄色,松散,该土层场地内普遍分布,层厚为0.00~2.90m,各项力学指标见表1。

表1 填土力学指标
2.2 有限元模型及边界条件
机场土质区的土裸露在空气中,在自然环境的影响下,土壤颗粒间的间距变大,土体相比于公路路基较为稀疏。在受到外力作用时会产生一定的变形,当外力作用撤去后,土体的变形将会产生一定的恢复,但无法复原至外力作用前的原样,所以土体的力学特性不属于弹性。材料的本构关系是反映材料力学性状的数学表达式,表示形式一般为应力—应变—强度—时间的关系[7],选择合适的本构模型能够合理模拟土体在动力荷载作用下产生的应力和变形。
土的常用弹塑性本构包含莫尔-库伦、修正莫尔-库伦、特雷斯卡和剑桥等力学模型。谢治堃在进行冲击荷载下典型土体力学响应试验研究及有限特征比理论分析研究中采用摩尔-库伦本构模型对土体进行数值分析[8]。莫尔-库伦适用于岩土工程中涉及到的换填、隧道、地基处理、边坡、采矿等工程,属于一阶模型,可在一定程度上描述岩土材料的特性,由于参数易于获取且一般情况下可以较好地描述土的破坏应力状态[9]。飞行区土面上部填土为均匀的细粒土,采用能够很好地模拟冲击荷载的莫尔-库伦本构模型[10]可以准确地描述机场土面区在PFWD作用下的受力情况。
在软件中建立土体和承载板的三维模型并对承载板施加动力荷载。模拟的PFWD落锤高度取80cm,落锤冲击荷载取10kN,由落锤及高度计算荷载到达时间为0.4s,落锤的作用时间为25ms,具体的模型参数如下:
1)土体模型:建立尺寸长、宽、高均为200cm的立方体。
2)土体本构:采用莫尔-库伦本构模型,模拟土体在承载板作用下发生的弹塑性变形。
3)承载板模型:建立直径为30cm,厚度为3cm的金属板。
4)承载板本构:模拟金属材料,采用弹性本构模型,弹性模量为210 000MPa。
实体模型见图4所示,对承载板上表面用几何功能画出与落锤直径相同的圆形曲线,选中曲线将模型沿着Z轴方向进行分割。完成分割后,承载板上表面被划分出两块区域,中心区域为加载区域。
建立模型后,对模型进行网格划分。首先对土体和承载板进行尺寸划分,土体播种间距为0.1m,承载板尺寸较小间距设置为0.05m。网格采用混合网格生成器划分,土体共生成9 206个节点和9 261个单元,承载板共生成50个节点和102个单元。经检查承载板与土体之间无自由面,每个节点连接4个自由面,网格质量良好。图5为整体模型生成网格后的模型,一共生成9 256个节点和9 363个单元。
图4 总体模型

图5 网格划分
划分结束后,对模型的边界条件进行设置[11]。做动力分析时,一般较少采用静力的边界条件(模型侧面约束法向方向自由度,模型底部约束3个方向自由度),这样能量无法透过固定边界向远处传播[12]。故上部面采用自由约束,底部为固定约束,模型的周围四面加自由场单元即无反射边界。这样,可让波沿着无限空间体开口方向无限传播,进而避免回弹振波对实验结果的影响[13]。
3 计算模拟结果分析
3.1 位移变形分析
为进一步观察外力变形产生的影响,首先使用运算器进行求解,计算结束后,提取相关的结果。土体在落锤的冲击下表面产生竖向变形即弯沉盆,不同类型土的弯沉盆不同,因此会对应产生不同类型的动态弹性模量。该机场土质区经过模拟后的竖向变形如图6所示,表面形成的弯沉盆分布,如图7所示,直径约为60cm。以弯沉盆左侧边缘为原点,依次向右以5cm为一个单位建立坐标系,得到模型截面竖向弯沉分布,如图7所示。根据图8中的数据分布规律发现,整体弯沉线的变形趋势在0~5cm和55~60cm范围内较为平缓;在靠近承载板边缘5~15cm和45~55cm的范围内急剧加大,接近承载板中心15~45cm范围内又渐变为水平,图中最大变形值约为17.7μm。

图6 竖向位移变形(um)
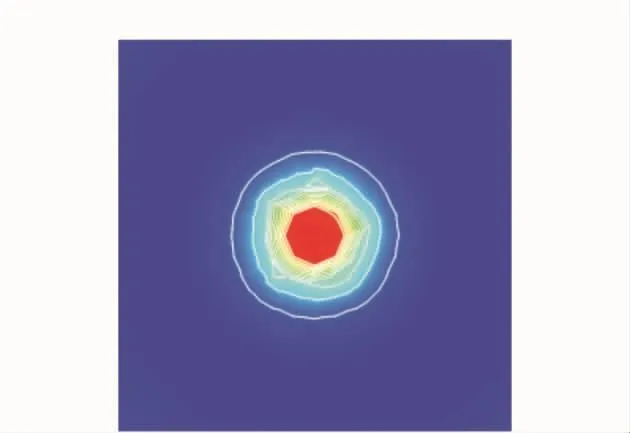
图7 表面弯沉盆分布
在冲击荷载作用下,土体除竖向变形外,还会产生水平位移变形。飞行区土面区宜尽可能植草,固定土面。飞行区内草高一般不应超过30cm,并且不得遮挡助航灯光和标记牌[14]。民用运输机场土质区植被对升降带内土体具有一定的保护作用[15],因此在分析PFWD对土体检测过程中产生的影响时,应考虑对测区植被的影响。
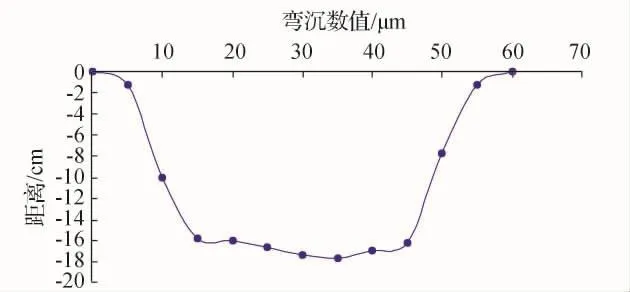
图8 弯沉盆数值变化
承载板两侧X,Y方向产生的水平位移呈对称分布,其中沿X轴的水平位移分布如图9所示,两侧的数值分别约为3.25μm、3.08μm。沿Y轴的水平位移分布如图10所示,两侧的数值分别约为3.22μm、3.09μm。
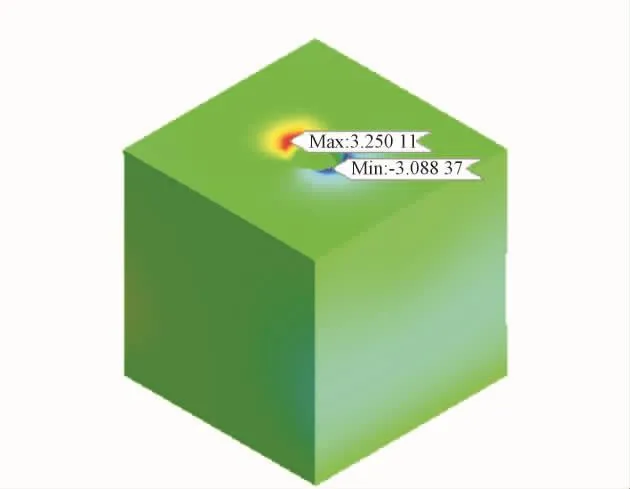
图9 X轴承载板两侧水平方向位移变形(um)

图10 Y轴承载板两侧水平方向位移变形(um)
从X,Y轴两侧产生的位移来看,当使用PFWD——便携式落锤弯沉仪检测时,落锤的冲击作用不会对测区的植被产生影响,有利于植被的保护。就土面区而言,检测过程中产生的微量变形不会产生较大影响,因此检测完成后的机场土面区只需按照日常标准维护作业,不需要额外加固。
3.2 竖向应力分析
提取不同深度所对应的应力数值,具体结果如表2所示。图11为根据结果绘制的深度-应力数值图,随着深度的逐渐增加,应力总体处于不断下降的趋势且下降趋势较为平缓,最大应力值出现在土体与承载板接触面上为0.42kPa,最小应力值出现在距离土体表面0.9m处为0kPa。范磊在利用PFWD进行土石混填路基压实质量快速检测方法研究时,曾定义一个表征应力衰减参数PS,探究冲击作用下的影响深度[16]。

表2 竖向应力数值表

图11 深度-应力数值
按式(2)计算应力衰减余量。

式中:PS为应力衰减余量;σ表为土体表面的竖向应力;σh为深度为h的竖向应力。计算结果如表3所示。
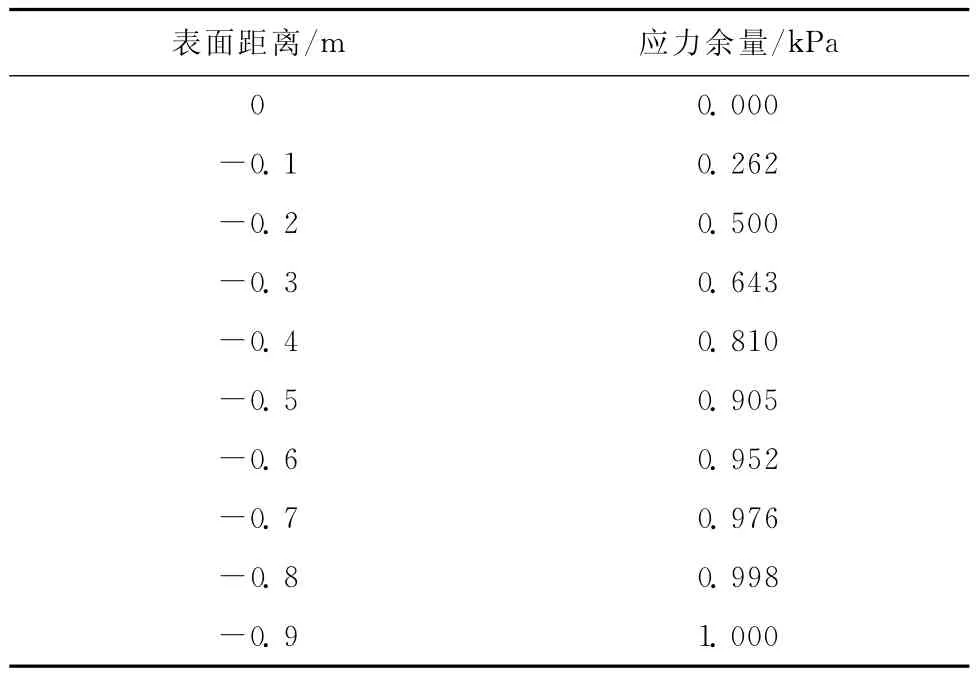
表3 计算结果
图12为应力衰减余量与深度变化曲线,由表中数据可知,整体模型的竖向应力影响深度为0.9m,竖向应力分布如图13所示。由于机场土质区的填土在自然状态下相比于高压实的路基显得较为疏松,所以动荷载造成的影响深度要略大于相同填料普通公路路基的影响深度。
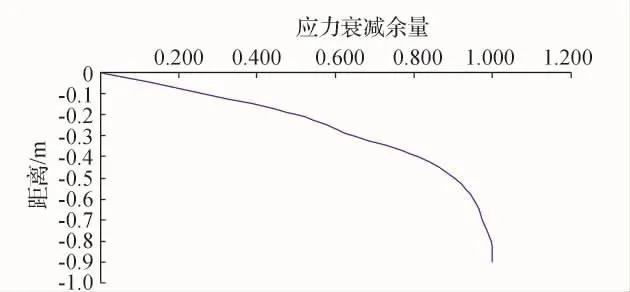
图12 测区土体应力余量随深度变化曲线

图13 竖向整体应力分布
结合计算所得的最大应力值和最大弯沉值,验算回弹模量所需的数据见表4。

表4 各项物理参数
将数据代入式(1),得到土体动弹性模量约为5.36MPa。根据式(3)将实地测得土体的压缩模量换算成土的静态弹性模量为4.23MPa。
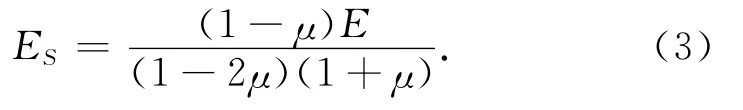
式中:ES为土体压缩模量;E为土体弹性模量;μ为土体泊松比。
因为5.36/4.23=1.3,所以比值结果符合土力学中关于动、静弹性模量规定关系。
由弯沉盆的分布范围,以弯沉盆数值变化图相同的坐标原点绘制横截面上不同位置竖向位移对应的土体应力分布图,如图14所示。
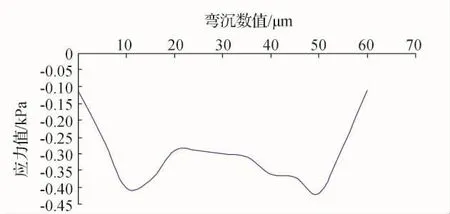
图14 不同位置弯沉位移对应的竖向应力分布
承载板直径为30cm,从坐标图上看,0~10cm和50~60cm范围内竖向应力随着弯沉竖向变形值的急剧增加而增加;最大的竖向应力分别在承载板两侧边缘处产生;15~45cm范围内的压应力值平均约为0.33kPa。
由式(4)计算测点土样的抗剪强度,其中土的抗剪强度与作用在剪切面上的方向应力的关系为:
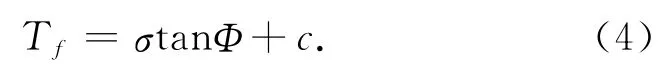
式中:Tf为土的抗剪强度;c为土的黏聚力;σ为剪切滑裂面上的法向应力;Φ为土的内摩擦角。
由于产生的压应力远小于土体的抗剪强度,所以土体在检测过程中不会发生破坏。
4 结 论
通过对PFWD在机场土质区检测并计算得到的力学结果,可以得出以下结论:
1)从竖向位移变形的影响范围来看,竖直方向上弯沉盆呈环状分布,直径约为60cm,最大竖向变形值为17.7μm,从水平位移变形的影响范围来看,沿X,Y轴产生的水平位移约为3μm,由于变形值较小,因此对测点承载板边缘附近的植被产生的影响较小,可防止检测过程对植被造成过多的破坏。
2)土体在落锤冲击的作用下产生的应力变化深度约为0.9m,产生的最大应力为0.42kPa,应力随着深度的增加不断降低,整体变化趋势较为平缓。由此结合最大应力值,推算得土质区土样的动弹性模量为5.36MPa,是原土样静弹性模量的1.3倍,比值符合相关理论。
3)承载板与土面接触范围内的平均压应力为0.33kPa,该值与最大压应力均不会对土体产生破坏。
