航空公司枢纽航线网络设计双层规划模型

汪 瑜，车 通，鄢仕林，张培文

（中国民航飞行学院 机场工程与运输管理学院，四川 广汉618307）

枢纽航线网络设计是指在一个网络中，给定若 干个机场位址、各OD（Origin－Destination）客流需求量以及航线上单位流成本等网络设计参数，对枢纽机场位址、机场之间的连接关系及OD客流路径进行系统安排，从而达到枢纽航线网络设计成本最小的目标。传统的枢纽航线网络设计模型多以枢纽网络设计航空公司为唯一决策者，且学者们对模型中的决策变量、优化目标和约束条件等方面进行了大量研究。这其中：决策变量从基于路段变量［1］，到基于四下标路径［2］，再到基于三下标变量［3］，实现了枢纽航线网络设计问题建模质量的提高；优化目标选择则包括了枢纽网络成本最小化［4］、运输时间最短［5］、环境影响最小［6］、等待时间最短［7］、枢纽最大延误时间最小［8］等方面；约束条件则均以完成网络中各OD客流需求量运输为基本要求，再结合问题类型设置一些条件，如节点容量限制［9］、拥堵限制［10］、运输时间限制［11］、中转次数限制［12］、非期望约束限制［13］、需求价格弹性［14］及鲁棒性条件限制［15］等。

可以发现，上述传统建模过程忽略了其它网络设计利益相关者（如竞争者、市场运营补贴提供者等）对于航空公司设计航线网络的影响，如目前国内大量属地化后的民用运输机场借助当地政府的资金扶持，不断引导航空公司开辟亏损空运市场，导致航空公司在设计枢纽航线网络时必须对空运市场补贴方案进行选择，因此，传统建模方法与现实不完全相符。在这方面，已有研究大多为基于Stackelberg博弈模型的双方决策者（做为领导方的已在某枢纽运营的航空公司和作为决策跟随方的新进入市场的航空公司），为获得期望市场份额而展开的枢纽选址问题研究。例如，MARIANOV等人考虑到市场竞争因素，建立了一个基于竞争环境的枢纽航线网络模型［16］；Lin等人研究了在寡头垄断市场下的枢纽航线网络设计博弈行为［17］；Villagra等人基于Stackelberg博弈模型探讨了市场新进入者枢纽选址、设计网络和定价问题，并采用宏启发式算法进行求解［18］；Mahmutogullari等人研究了一个以确保竞争航空公司在Stackelberg竞争中市场份额最大化的双头垄断航线网络设计模型［19］；Niknamfar等人以市场份额最大化和枢纽航线网络设计成本最小化为多目标函数构建了竞争环境下的双目标规划模型［20］；Ghaffarinasab等人构造了竞争环境下的单分配与多分配枢纽选址问题模型，并利用CAB和TR数据集验证了模型的可行性［21－22］。本文构建的枢纽航线网络数学模型，仍然以航空公司为网络设计的唯一决策方，所不同的是，空运市场运营补贴提供者会根据航空公司的枢纽航线网络设计方案开展补贴定价方案决策，并将决策结果反馈给航空公司，从而影响枢纽网络设计结果。因此，可将航空公司作为上层，决策目标为枢纽网络设计成本最小化，决策内容为选择枢纽机场位址、节点间连接关系、O＆D流路径和空运市场补贴方案；市场运营补贴提供者作为下层，决策目标为各市场补贴提供者运输OD客流需求量最大化，决策内容为空运市场补贴定价。最后，本文选取国内24个城市数据来验证模型的可行性。

1 假设条件、符号说明和问题描述

影响枢纽航线网络设计的因素较多，如国际金融与贸易、市场经济环境、运输产业政策、航空公司战略目标及市场开发能力等，但最直接和根本的影响因素仍为航空运输需求量，即在满足运输需求量的基础上获取最大的经济效益。因此，本文研究的枢纽航线网络设计问题，是在航空公司选定待开发的各OD对客流需求量，以及市场补贴提供者提供的各市场补贴价格引导基础上，就枢纽机场数量及其位址、机场连接关系、客流运输路线及补贴方案开展系统安排。

1.1 假设条件

结合文献［1］—文献［3］，给出以下假设条件：

1）枢纽航线网络决策者为航空公司，补贴定价决策者为市场补贴提供者，且需要形成对航空公司的反馈；

2）任意OD客流运输路径至多包含三条边，也即最多经过两个枢纽机场进行中转运输；

3）轮辐机场允许与多个枢纽机场相连接，且它们之间允许直达运输；

4）所有OD客流需求量都是固定的，且必须由起始地运输到目的地，并运完；

5）各枢纽机场之间存在运输规模经济性，并用折扣因子来表示；

6）各枢纽机场具有容量限制。

1.2 符号说明

n：上层航空公司网络中的机场总数，i，k，m，j∈ ｛1，2，…，n｝；

S：下层空运市场运营补贴提供者（节点）总数，s∈ ｛1，2，…，S｝；

Ls：下层空运市场运营补贴提供者s提供的补贴方案总数，l∈ ｛1，2，…，Ls｝；

ηskl：示性算子，当下层空运市场运营补贴提供者s的补贴定价方案l通过枢纽k中转时，取值为1，否则为0；

φls（i，j）：示性算子，当下层空运市场运营补贴提供者s的补贴定价方案l起终点分别为i和j时，取值为1，否则为0；

δsjl：示性算子，当下层空运市场运营补贴提供者s的补贴定价方案l的起点或终点为j时，取值为1，否则为0；

：示性算子，若市场运营补贴提供者s的补贴定价方案l曾报价给航空公司，且被拒绝过，则为1，否则为0；

Γk：枢纽机场容量限制。

1.3 问题描述

上层决策者：已知网络中有n个机场节点、各OD客流需求量Wij及其单位流成本cikmj（cikmj＝cik＋αckm＋cmj，其中α为折扣因子，0≤α≤1）、各节点的枢纽设置成本Hk及其数量q、市场运营补贴提供者s提供的补贴定价方案l（用特定客流路径及相应的补贴定价费用来表示）的预期运营利润、优化枢纽位址yk、各OD客流在中转运输路径i－km－j及直达运输路径i－j上分别流经的比例xikmj和xij，确定各补贴定价方案接受与否，以实现枢纽航线网络设计成本最小化，并将决策信息传递给下层模型。

下层决策者：已知各自补贴费用总额Vs、各补贴定价方案l的OD客流需求量及补贴定价费用成立，其中分别为补贴方案l的运输费用和OD客流需求量的运输收入），结合上层航空公司反馈的枢纽位址yk和各补贴定价方案接受与否的信息，开展各OD客流市场的补贴定价决策，以实现在各自补贴费用Vs总额限制下的OD客流需求量运输最大化，并将决策信息反馈给上层。

因此，上层模型的控制变量为xikmj、xij、yk和，其中yk和为下层模型决策变量的反应函数，并实现下层对上层的反馈作用。

2 模型结构

为达成航空公司枢纽航线网络设计成本最小化、市场补贴提供者的运输OD客流需求量最大化目标，本文构造了双层规划模型。与传统模型相比，本文构建的枢纽航线网络双层规划模型增加了空运市场补贴决策变量，且此决策变量在上层模型中受枢纽航线网络设计方案影响，之后又在下层模型中对补贴定价方案进行反馈。因此，本文所构建的模型除传统模型中多次提及的枢纽机场位址、节点间连接关系及OD流路径外，还增加了空运市场补贴作为决策变量。

2.1 上层模型

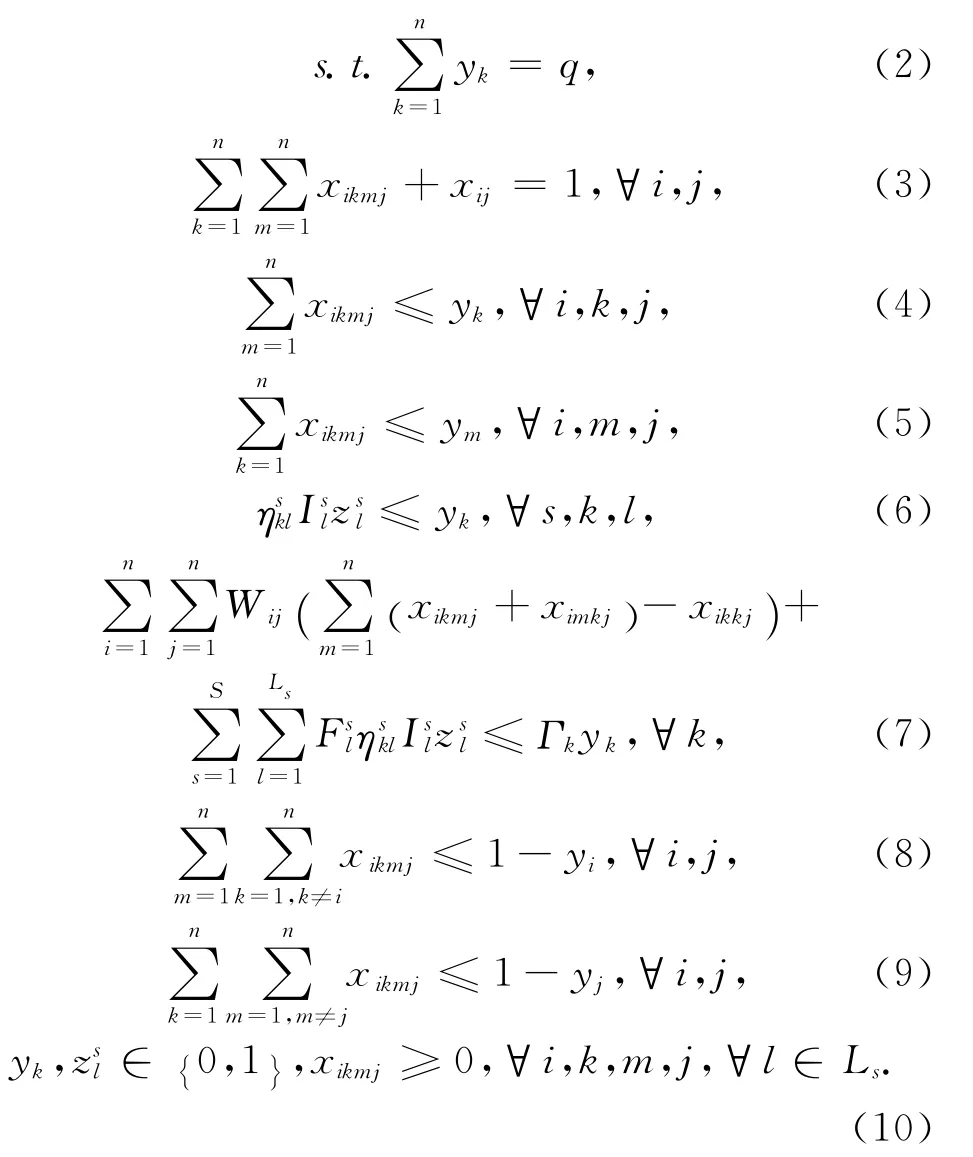
该上层模型是一个非严格的枢纽航线网络设计模型［12］。目标函数（1）为枢纽航线网络设计成本最小化；式（2）为枢纽机场数量的约束；式（3）为OD客流需求量运输完整性约束；式（4）和式（5）约束了OD客流中转必须在枢纽上；式（6）约束了只有包含枢纽机场的补贴定价方案才能被选择；式（7）规定了枢纽机场允许的最大客流量；由于枢纽间的运输存在折扣系数，因此枢纽之间必然采用直达运输，枢纽与轮辐机场之间最多只能中转一次，其约束如式（8）和式（9）所示；式（10）规定了决策变量的类型与取值范围。

需要说明的是，式（8）和式（9）不仅限定了不同类型节点之间OD对流量的转运方式，而且还限定了这种转运方式的路径表达形式：当节点i和j都为枢纽时，式（8）和式（9）左手项中的变量必须全部为零，导致该OD客流的路径形式被限定在i－i－j－j；当节点i和j中一个为枢纽、一个为非枢纽时，式（8）和式（9）的左手项中必有一个变量全部为零，导致该OD客流的路径形式被限定在i－i－m－j或i－k－j－j，以此保证通过各枢纽节点流量计算的准确性。

2.2 下层模型

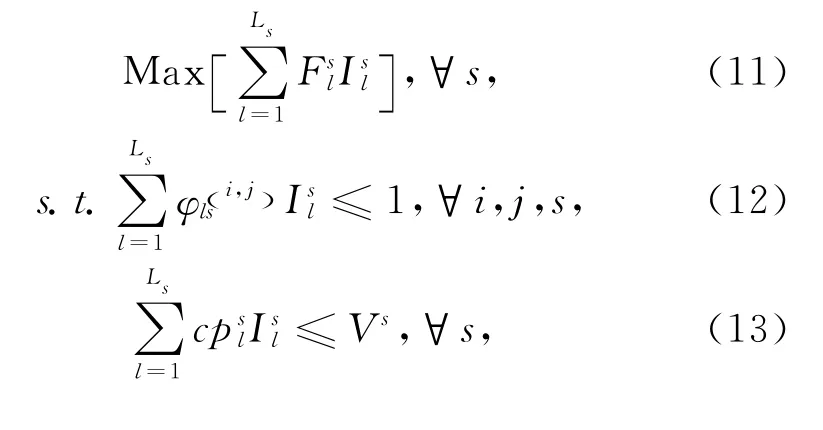
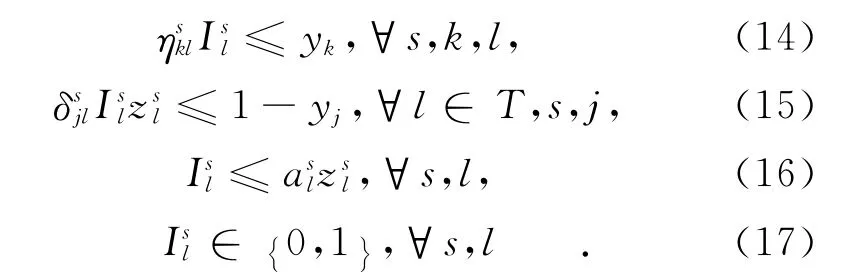
由于下层模型对于市场运营补贴提供者s来说是解耦的，因此可分开求解。式（11）为模型的目标函数，表示市场运营补贴提供者s运送的OD客流需求量最大化；式（12）为市场运营补贴提供者s的任意一个OD客流补贴方案被选中的数量不超过1个；式（13）为市场运营补贴提供者s用于补贴的资金总额度约束；式（14）规定了补贴方案路线的中转点只能包含上层给定的枢纽机场；式（15）保证了在市场运营补贴提供者s提供的补贴方案路线类型为一次中转、且起点或终点为枢纽机场时（记为集合T）的补贴方案，补贴方案路线采用s－j－j－j或者j－j－j－s形式，以此确保上层航空公司选择该类补贴方案路线时，其客流量纳入该枢纽容量的统计中；式（16）保证了补贴定价方案未被选择后不再报价给上层航空公司；式（17）为对决策变量类型的约束。

3 迭代求解步骤

上层航空公司为了保证枢纽航线网络设计成本最优，在初始网络设计时要求空运网络设计参与者既要提供备选枢纽集，也要提供相应的空运市场补贴定价方案，并要求随着上下层交互直到补贴定价方案稳定为止。考虑到Yalmip平台下Gurobi求解器能够在可接受的时间范围内对上述模型实现求解，因此采用以下迭代步骤直接求解该模型。

第2步：令t＝t＋1，对下层模型求解，获得决策变量（Isl）t的取值，并反馈给上层；

4 算例分析

选取近10年中国城市航空客运年吞吐量排名稳定在前8位的城市：北京市、上海市、广州市、成都市、昆明市、深圳市、西安市和重庆市（用序号1～8分别表示）。另外，选取分布于华北、华东和西南区域的航空客运年吞吐量小于200万人次的中小型机场，共16个城市，分别为包头、赤峰、鄂尔多斯、通辽、海拉尔、北海、柳州、满洲里、腾冲、德宏、湛江、台州、大理、武夷山、义乌和香格里拉（用序号9～24分别表示，且将每个机场视为一个空运市场补贴提供者）。客流量数据来自于国际航空运输协会MIDT（Market Information Data Types）和 SRS（Schedules Reference Service）航班计划（限于篇幅，原始数据略去）。24个城市对共统计到254个OD市场数据，通过整理2016年国内某航空公司的生产成本相关数据，获取运营收益数据和各OD对的单位流成本。考虑到枢纽航线网络设计结果受不同补贴定价方案的影响，本文将各OD对全部可行的补贴定价方案路线列出，计算得到了所有补贴定价方案所对应的运营成本，再通过与补贴因子相乘作为该补贴定价方案的最终补贴费用。文中8个枢纽机场的设置成本由2016年民航业发展统计公报和《中国民用航空第十三个五年规划》汇总，并按照各城市机场的年旅客吞吐量占比，根据一定比例修正获得［23－24］。算法程序使用 CPU2.4Hz，8G 内存机器，采用YALMIP工具的GUROBI求解器实现（ε≤0.001）。

4.1 结果分析与对比

为说明所提方法具有的优势，本文与无市场运营补贴提供者参与下的枢纽航线网络设计方案进行对比，对比的重点包括枢纽机场的数量及其位址、机场之间的连接关系及客流路线等方面。在整个对比分析过程中，进一步结合我国航线网络的实际情况［25］，并以此说明本文模型的合理性和可行性。

1）本文方法决策结果。从表1可以发现，在不同的网络设计参数（即枢纽个数、补贴因子和折扣因子）设置下，枢纽位址存在不同程度的变化，说明市场补贴提供者参与的力度（即单位补贴费用和投入补贴资金总额）能够影响航空公司枢纽航线的网络设计。另外，北京、上海、广州和成都是枢纽位址最频繁的选择，这与现实中枢纽机场选择结果相吻合。但当枢纽之间的运输规模经济性欠佳（折扣因子为0.8）时，枢纽位址选择出现了昆明和重庆，这是由于昆明和重庆的枢纽建设成本相对较少，且各OD客流流经昆明和重庆的运输成本较低所致。

2）传统方法决策结果。从表2可以发现，枢纽机场之间的运输规模经济性（折扣因子变化）对于枢纽位址的选择结果有着明显影响，这与文献［26］的研究结果一致。但从OD客流路线来看，枢纽航线网络设计结果中存在一定数量绕航率很高的OD客流路径，即不合理OD客流路径选择结果（数据列表略去），如广州－重庆的客流路线选择是广州－成都－重庆，明显与现实情况不符。

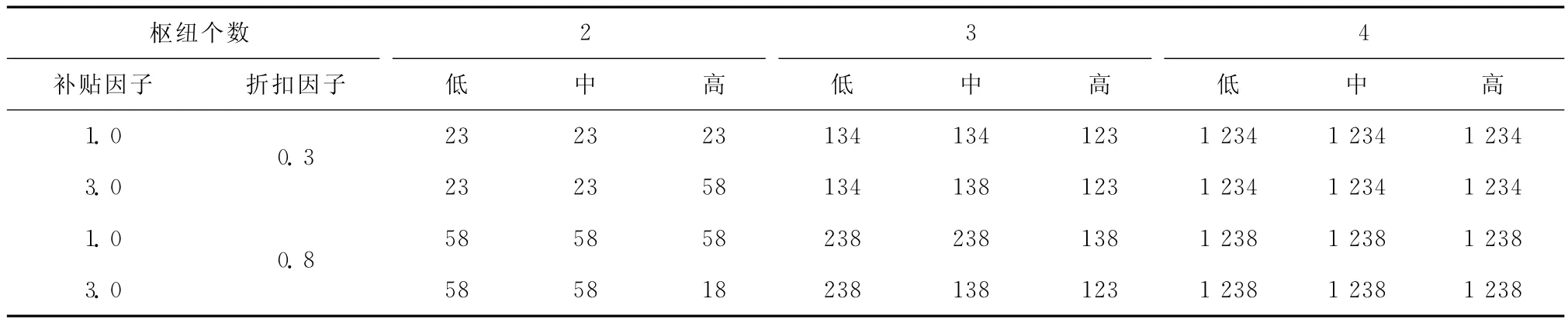
表1 枢纽航线网络设计方案

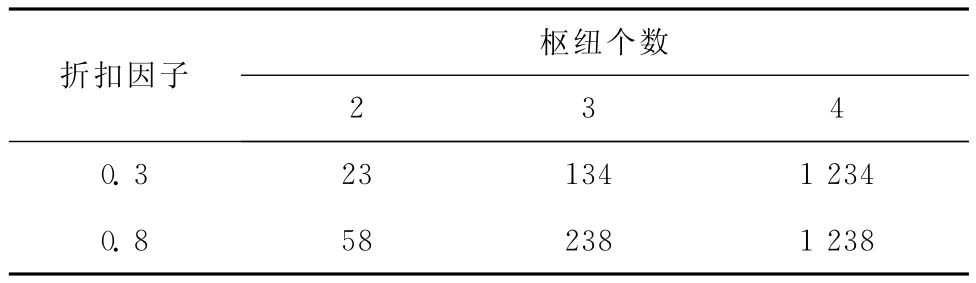
表2 无市场运营补贴提供者的枢纽网络方案

3）计算结果对比。从枢纽位址选择结果来看，本文方法的结果更为合理，如枢纽个数为3、折扣因子为0.3时（如表1第3行第8列所示），选择的北京、上海和广州为枢纽机场，而传统方法选择的是北京、广州和成都，显然前者更符合现实情况（见图1、图2）。

图1 无市场运营补贴提供者的枢纽航线网络设计方案

需要说明的是，在高补贴因子（补贴因子为3）下，枢纽机场从上海和成都（表2第2行第2列所示）变化为昆明和重庆（表1第4行第5列所示），这是由于随着补贴因子变大，更多的由于改变航空公司原本OD客流路线的运营成本产生的增加量，被吸纳补贴定价方案所获得的运营利润增加量抵消，从而使OD路线及枢纽的位址选择更加灵活，这也是昆明和重庆枢纽建设成本相对较低等原因综合所致。从客流路线选择结果来看也更为合理（数据列表略去），如广州－重庆客流路线在传统方法中选择的是广州－成都－重庆，而在本文方法中选择的是广州－重庆直达方式，显然后者更符合实际情况。

图1和图2分别给出了传统方法和本文方法所得出的枢纽航线网络设计方案。可以发现，从机场的连接关系看，与传统方法给出的结果相比，本文给出的设计方案更注重枢纽间的干线连接，通过轮辐航线继而扩大航线的网络覆盖范围。因此，市场补贴提供者参与下的枢纽航线网络设计方案更加符合枢纽航线的网络设计标准，并对航空公司开展枢纽航线网络设计决策具有更好的参考价值。

4.2 网络设计参数的灵敏度分析

由上述分析可知，枢纽航线网络设计参数对枢纽航线的网络设计方案具有重要影响。区别于传统模型，本文所构建的双层规划模型主要研究空运市场补贴因素与设计方案相互间的影响，因此，本文着重开展各市场补贴提供者的补贴资金总额以及直达运输补贴因子（以下简称“直达补贴因子”）对网络设计方案的影响。

图3给出了航线网络设计总成本受补贴资金总额的影响程度。为方便对比，本文将不同直达补贴因子下的航线网络总成本取平均值并作图分析。可以发现：随着补贴总额的上升，航线网络设计总成本不断下降；相同补贴总额下枢纽间运输的折扣因子越小，航线网络设计总成本就越小，且枢纽机场设置个数的增加会使航线网络设计总成本下降的更快。航线网络设计总成本下降是因为随着市场补贴额度增大，市场补贴提供者能够提供更多的补贴方案给航空公司，使得航空公司所吸纳的OD市场补贴方案及获得的运营利润更多。在相同补贴总额下枢纽机场间的折扣因子越小，完成相同路径上OD客流运输的费用就越少，从而使航空公司运输该OD客流所获取的运营利润就越高，由此导致航线网络设计总成本越小。另外，枢纽设置数量增加，会使航空公司即使在吸纳相同数量的补贴方案下，折扣因子越小所获得的运营总利润就越多，从而使航线网络设计总成本下降的更快。

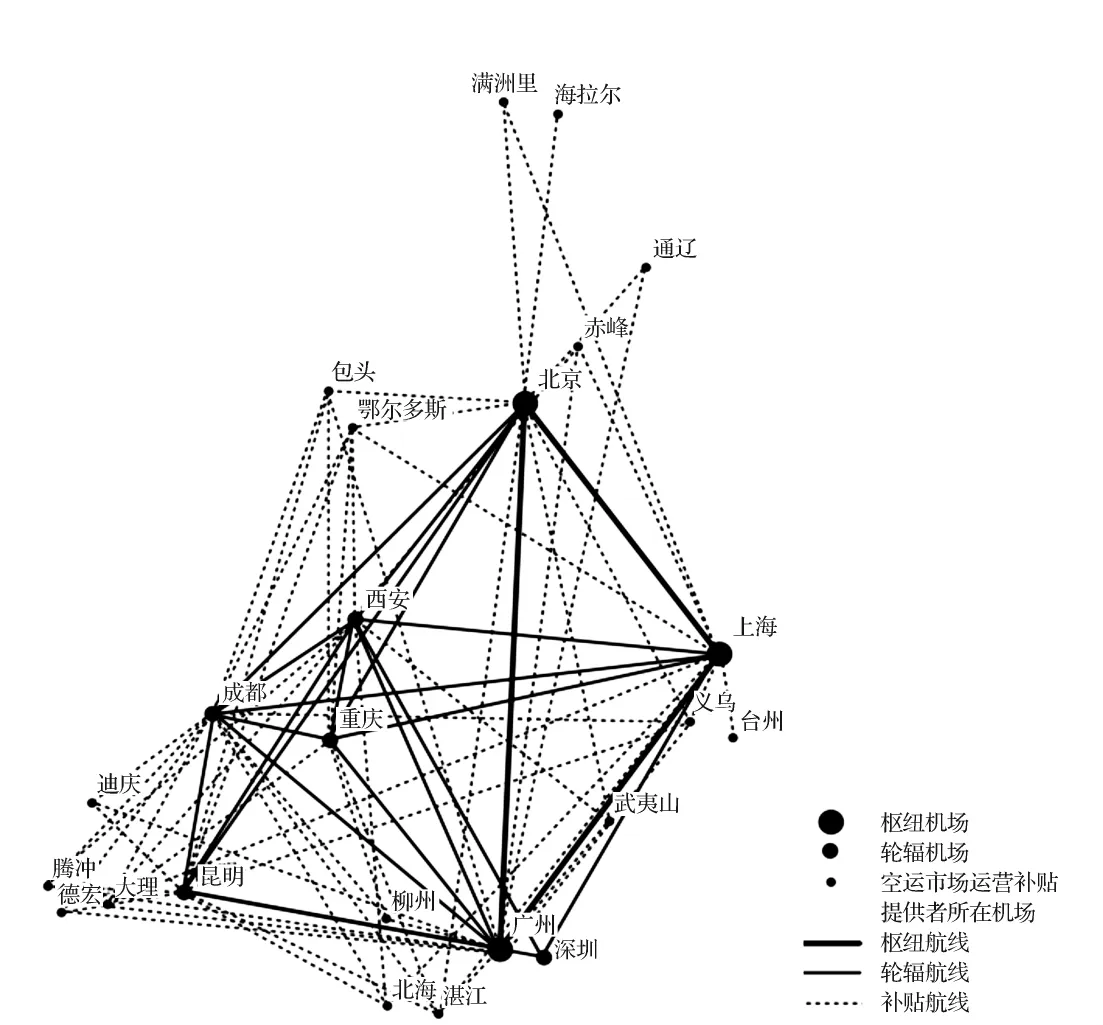
图2 市场运营补贴提供者参与下的枢纽航线网络设计方案

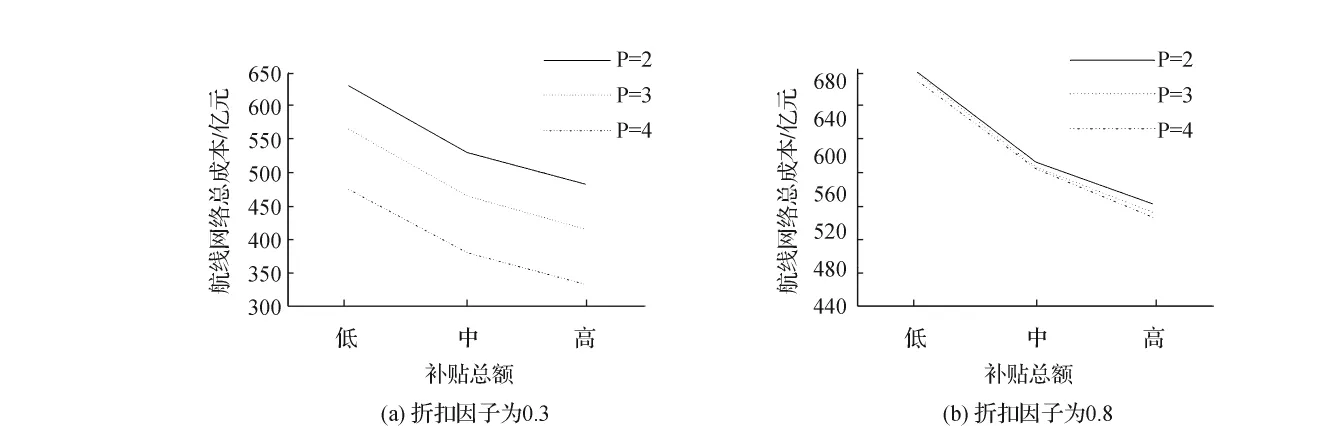
图3 补贴总额对航线网络总成本的影响

图4和图5分别给出了直达补贴因子对OD客流直达率和枢纽航线网络设计总成本的影响。为便于对比分析，本文将不同补贴总额下的航线网络总成本取平均值并作图分析（非直达补贴因子＝1.5）。从图4可以发现，随着直达补贴因子的变大，在0～1之间时直达率上升，大于1后直达率下降；相同直达补贴因子下的折扣因子越小，直达率越高，且枢纽机场设置个数增加会使直达率下降更快。

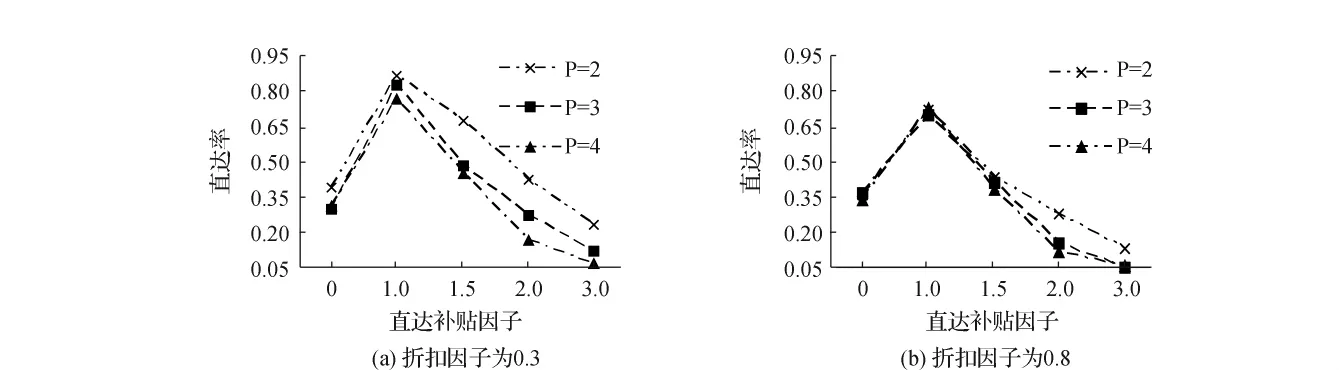
图4 直达补贴因子对OD客流直达率的影响

图5 直达补贴因子对航线网络总成本的影响

0～1 之间直达率上升是由于补贴方案产生的运营利润由负数逐渐变为正数，导致航空公司接纳直达补贴方案数量增加所致；而1以后下降是由于补贴总额一定下，随着OD客流直达运输补贴额度的上升，市场补贴提供者为了保证运输总量最大化而选择更多的OD市场数量，倾向于提供给航空公司更多的中转运输补贴方案，由此导致枢纽航线网络中的直达补贴方案减少。在相同直达补贴因子下枢纽机场间的折扣因子越小，完成相同路径上OD客流中转运输的费用就越少，从而使得中转运输该OD客流所获取的运营利润就越高，由此可使航空公司接纳更多的中转运输补贴方案，导致直达率更低。此外，随着枢纽设置数量的增加，折扣因子越小获得运营利润越多的中转补贴方案会被航空公司采纳的更多，导致直达率下降的更快。

从图5可以发现：随着直达补贴因子的增加，航线网络设计总成本不断下降；相同直达补贴因子下枢纽间运输的折扣因子越小，航线网络设计总成本就越小，且枢纽机场设置个数增加会使航线网络设计总成本下降的更快。航线网络设计总成本下降是由于直达补贴因子的增加，航空公司吸纳相同OD市场直达补贴方案获得的运营利润更多所致。在相同直达补贴因子下枢纽机场间的折扣因子越小，完成相同路径上OD客流中转运输的费用就越少，从而使得航空公司中转运输该OD客流所获取的运营利润就越高，由此导致航线网络设计总成本越小。另外，枢纽设置数量增加会使航空公司即使在吸纳相同数量的补贴方案下，由于折扣因子变小所获得的运营总利润增多，从而使航线网络设计总成本下降的更快。

5 结 语

针对市场运营补贴提供者向航空公司提供补贴报价影响枢纽航线网络方案的问题，本文提出了非严格枢纽航线网络设计与空运市场补贴定价的联合决策模型，即航空公司枢纽网络设计决策被视为上层模型，空运市场补贴定价决策被视为下层模型，算例分析结果表明，本文的设计模型切实可行。另外，补贴总额和直达补贴因子是影响枢纽航线网络设计方案的重要因素。下一步可基于网络设计参数的不确定性来研究枢纽航线网络设计与空运市场补贴定价的联合决策问题，以提高枢纽航线网络方案的抗风险能力。