新冠疫情下医疗废物管理的选址-分配优化
2020-11-19赵佳虹凌雅婷
赵佳虹,凌雅婷
(广东工业大学 土木与交通工程学院,广东 广州510006)
2020 年初,全球新型冠状病毒肺炎疫情爆发,医疗机构和城镇社区产生了大量含新冠病毒的纱布、口罩、护目镜和防护服等医疗废物。与生活垃圾管理[1]不同,新冠疫情下的医疗废物是具有高度感染性和高依附于外部环境的危险废物,因此,考虑环境系统的时变特性,合理度量回收处理活动的风险,降低环境污染和人员传染是集运医疗废物的首要任务和必要条件。
医疗废物管理系统包含废物回收、加工和处置环节[2-3]。医疗废物主要分为感染性、病理性、损伤性、药物性和化学性废物,其中,药物性废物是“可回收部分”,可直接运往回收点;损伤性、药物性和化学性废物是“可加工部分”,需运往加工点分解为可回收和可处置物质;感染性和病理性废物则属于“可处置部分”,需直接运往处置点。新冠疫情产生的医疗废物含有传染性强、传播途径多、环境依附性强、潜伏期长的病毒,废物残余仍然可能具有危害性,因此,需要从决策优化角度,合理规划医疗废物管理的设施选址和路线上的运量分配问题。
医疗废物的研究方法沿用了危险废物管理优化领域的研究成果,学者们先后通过风险度量、系统建模和算法设计,协同优化了危险废物管理的设施选址、路径选择等决策。在风险度量方面,构建了传统风险模型[4]、感知风险模型[5]、期望方差和反效用模型[6]及“暴露人口吨数”模型[7];Verma和Vedat[8]构建了扩散模型,评估危险废物泄露对大气环境的影响;Zhao和 Vedat[9],以及 Eric等人[10]设计了环境风险度量模型。在优化建模与求解方面,Li等人[11]以跨省市区域型危险废物物流系统为基础,优化配置了中心选址、运量分配等决策。Ardjmand等[12]设计了带优先权的遗传算法来提高求解效率;Asgari等[13]考虑了“废物-技术”相容性约束,解决了现实问题中近似优化解的求解难题;Rabbani等[14]设计了“废物-废物运输”相容性约束,采用NSGA-II方法求解。胡佳等人[15]设立了公平性目标,解决危险废物多次往返运输的风险均衡问题;Zhao等人[16]考虑了废物设施能力与路段风险承载能力约束,优化设施选址、废物分配和运输决策。
在新冠疫情下,以上研究成果的适用性存在以下不足:1)忽略了废物处置的风险管理。新冠疫情下产生的医疗废物,其可处置部分的潜在危害巨大,因此,废物处置点的管理也需要考虑风险控制;2)风险模型难以评估新冠病毒的传播风险。病毒传播途径以飞沫传播为主,飞沫以外部环境为媒介(如空气混合并形成气溶胶,或依附于外部环境中的物品表面),人体通过吸入或接触环境中的新冠病毒而诱发感染。风险度量需要结合环境系统,从人口和环境两个层面联合控制二次传染;3)模型和方法的鲁棒特性分析不足。作为新冠疫情的衍生问题,医疗废物的回收处理需要充分结合当前实际,通过计算对比不同规模和参数条件下的优化结果,推演出具有可操作性的实践方案。
综上所述,本文以新冠疫情下的医疗废物管理系统为基础,以联合控制时变的环境和人口风险为目标,协同优化医疗废物的设施设备规划和运量分配方案。具体考虑了新冠病毒的传染性和环境依附性,设计时变“环境-人口”风险度量方模型,并将其引入到医疗废物管理系统的选址-分配模型中;针对模型求解的复杂性,设计基于切比雪夫方法的多目标优化方法;最后,通过多个不同规模的算例来验证模型和算法的有效性。
1 时变“环境-人口”风险度量
新冠病毒的传播以空气为主,主要表现为:病毒以飞沫为主要载体,通过人体吸入飞沫、气溶胶,以及人体接触附有飞沫的物品,形成传播扩散。飞沫的喷洒、蒸发、沉积等活动对外部环境具有强烈的依附性,因此,新冠病毒的扩散与周边的实时环境条件(如风速、风向等)密切相关。本文主要分析新冠病毒在大气环境中的传播风险:暴露于大气环境中的病毒受到横纵向风的影响,动态传播形成立体的“病毒场”;随着时间的推移,病毒场的范围以及场内的病毒含量不断增加,周边居民则会通过吸入或接触而遭受病毒传染。为实时反映环境的毒害程度和潜在的受害人数,本文将新冠疫情下医疗废物的传播风险界定为一类时变“环境-人口”风险(EPR),即在时变条件下,病毒场中病毒含量(CON)和周边的居民总数(POP)的乘积,即
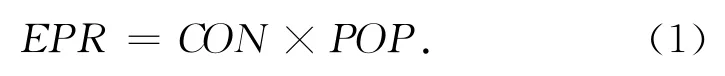
由于横向和纵向风的共同作用,医疗废物中的新冠病毒会在周边环境中进行随机的立体式传播,传播范围具有以下特点:1)由于横纵向存在风速差,风险传播横切面图应以泄露源为圆点,按照横向风吹拂方向形成一个椭圆形(见图1);2)横向风的吹拂角度可基于水平地面随机旋转,为更全面地预测病毒传播范围,本文将病毒场的横切面描述为:在地面横向风(风速为μα)的作用下,病毒以泄露点为圆心,以图1的椭圆形为传播扇叶,在传播时间T内,基于水平底面360°旋转传播形成一个圆(见图2),该圆的半径L为横向风速和传播时间的乘积;3)如图3所示,在纵向风(风速为μβ)的协同作用下,图2的圆以水平地面为基准,在时间T内向上推移,形成一个圆柱体,该圆柱体高度H为纵向风速和时间的乘积;4)借鉴箱式模型原理,设定病毒在圆柱体内均匀分布,则病毒含量可表示为病毒泄露总量和圆柱体体积的商,即
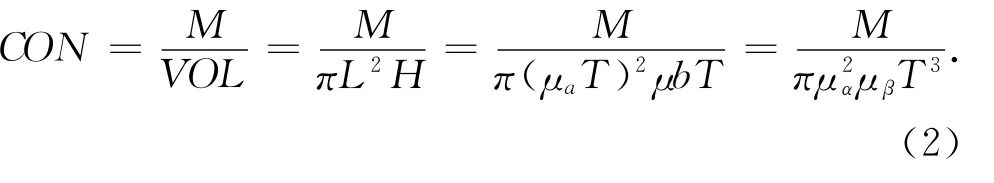
若ρ为事故点附近的人口密度,那么在T时刻,暴露于该圆柱体内的人口数量为
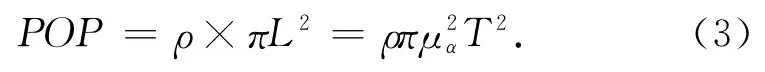
将传播时间T分解为s个离散的基本时间元ts,且s∈S,则有

将式(2)—式(4)代入到式(1),可得到时变“环境-人口”风险度量模型为


图1 恒定横向风下的风险传播横切面

图2 风险传播横切面
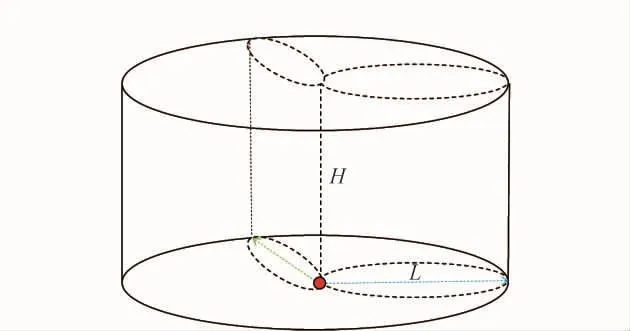
图3 风险传播立体图
2 模型构建
2.1 问题描述
医疗废物管理的选址-分配问题旨在优化回收点、加工点和处置点的建设位置,且能够合理分配各条运输路线上的废物运输量,具体内容包括:1)在候选点中确定回收点的建设位置;2)在候选点中确定加工点的建设位置;3)在候选点中确定处置点的建设位置;4)确定产生点和各设施之间的医疗废物运输量。本文构建的医疗废物管理选址-分配多目标优化模型,设计总时变“环境-人口”风险和总成本最小化两个优化目标,其中,风险主要来源于设施选址,成本则包括选址和运输成本。
2.2 基本假设
构建模型前设定假设条件为:1)对医疗废物的可回收、可加工及可处置部分依次设定,分别为可回收废物、可加工废物和可处置废物;2)各设施收集处理的医疗废物总量可计为潜在泄漏量;3)各种设施要达到能够同时处理医疗废物可回收、可加工及可处置部分的技术要求;4)运输车辆都应满足同时运输医疗废物可回收、可加工及可处置部分的安全要求;5)运输环节不考虑道路的容量限制和风险承载能力限制;6)新冠疫情下的医疗废物具有高度感染性,其回收处理活动可适度弱化设施的新建、运营及单位运输成本。
2.3 符号说明
2.3.1 集合
设N(V,E)为医疗废物运输网络,其中,V=G∪R∪B∪D。
G为医疗废物产生点集合;
R为回收点的建设候选点集合;
B为加工点的建设候选点集合;
D为处置点的建设候选点集合;
S为传播时间节点集合。
2.3.2 定量
RFCi,MFCi和DFCi分别为回收点、加工点和处置点i∈O∪P∪Q的建设成本;
RTC,TTC和DTC分别为可回收、可加工和可处置废物的单位运输成本;
RCi,MCi和DCi分别为回收点、加工点和处置点i∈O∪P∪Q的最大处理能力;
gi为产生点i∈G的产量;
φ,θ分别为废物中可回收和可加工的百分比;
δ为加工后的可回收百分比;
μβ为地面纵向风的风速;
ts为传播时刻,s∈S;
ρi为节点i∈V的人口密度;
RN,MN和DN均为正整数,依次为回收、加工和处置点的建设数量,则有
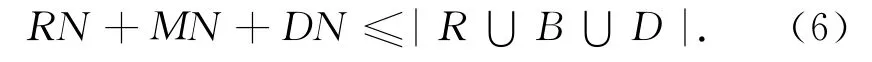
2.3.3 变量
xij为连续变量,表示由产生点i∈G到回收点j∈R的可回收废物运量;
yij为连续变量,表示由产生点i∈G到加工点j∈B的可加工废物运量;
zij为连续变量,表示由产生点i∈G到处置点j∈D的可处置废物运量;
lij为连续变量,表示由回收点i∈R到处置点j∈D的可处置废物运量;
mij为连续变量,表示由加工点i∈B到回收点j∈R的可回收废物运量;
nij为连续变量,表示由加工点i∈B到处置点j∈D的可处置废物运量;
oi为0-1变量,若建立回收点i∈R,则为1,否则为0;
pi为0-1变量,若建立加工点i∈B,则为1,否则为0;
qi为0-1变量,若建立处置点i∈D,则为1,否则为0;
ui为连续变量,表示回收点i∈R处理的可回收废物总量。
vi为连续变量,表示加工点i∈B处理的可加工废物总量。
wi为连续变量,表示处置点i∈D处理的可处置废物总量。
2.4 多目标选址-分配模型
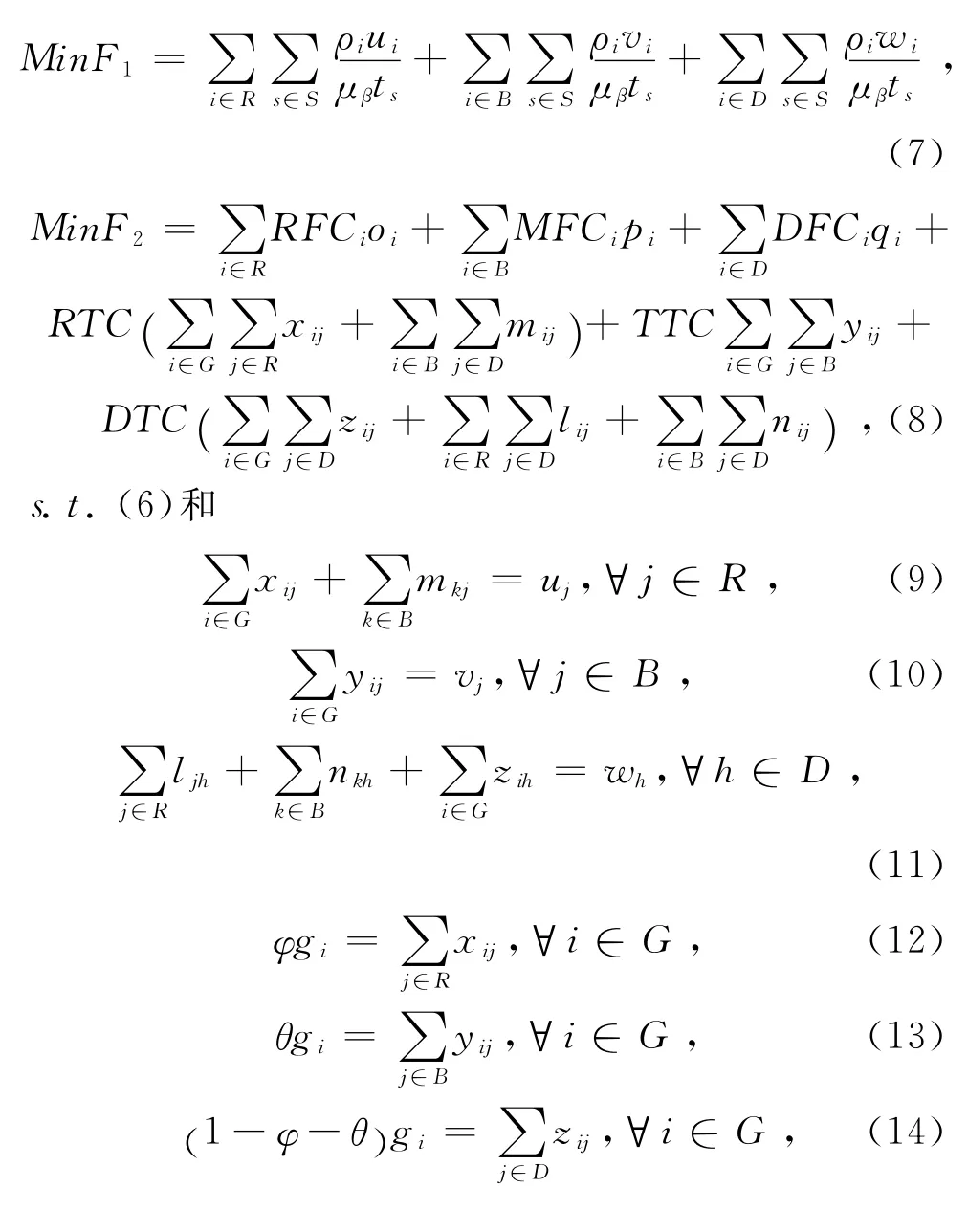

目标函数(7)表示总时变“环境-人口”风险最小化,主要包括建设回收点、加工点和处置点的风险;目标函数(8)为总成本最小,包含各设施的建设成本,以及各类医疗废物的运输成本。式(9)—式(26)为模型约束条件。其中,式(9)—式(11)分别为可回收、可加工及可处置医疗废物的流量守恒约束;式(12)—式 (14)为产生点与各设施之间的流量守恒约束;式(15)—式(17)为各加工点之间的流量守恒约束;式(18)—式(20)分别为回收点、加工点及处置点的能力约束;式(21)—式(23)为设施的建设数量约束;式(24)—式(26)为决策变量定义域。
3 求解方法
本文构建的是一个0-1混合整数目标线性规划模型,包括离散型和连续型变量,设有总风险和总成本最小的两个不同量纲优化目标。假设网络有产生点g个,回收、加工和处置点的建设候选点o,p和q个,则上述模型共有o+p+q个0-1决策变量,6e+o+p+q个连续决策变量和3g+3o+4p+2q+3个约束条件。通常,求解多目标模型的常用方法有线性加权[16]、随机规划[18]及启发式算法[19]等。本文综合考虑决策者偏好和Pareto最优解集[20]的鲁棒性,采用字典式赋权切比雪夫方法[21-22],设计多目标模型求解方法,即采用极值法统一两个优化目标的量纲;设定两个目标函数的权重系数;采用字典式赋权切比雪夫方法将多目标模型转化为单目标模型;通过代入参数,直接求解转化后的单目标模型。具体求解步骤设计如下:
步骤1:设置集合G,R,B,D,S,令X={xij,yij,zij,lij,mij.nij,oi,pi,qi,ui,vi,wi}为决策变量向量,F1(X)和F2(X)为两个目标函数式;H为可行域。
步骤2:输入参数RFCi,MFCi,DFCi,RTC,TTC,DTC,RCi,MCi,DCi,gi,φ,θ,δ,μβ,ts,ρi。
步骤3:分别以F1(X)和F2(X)为目标函数构建单目标模型,并求得最优解和。
步骤4:设置无量纲化因子σ1和σ2,其中
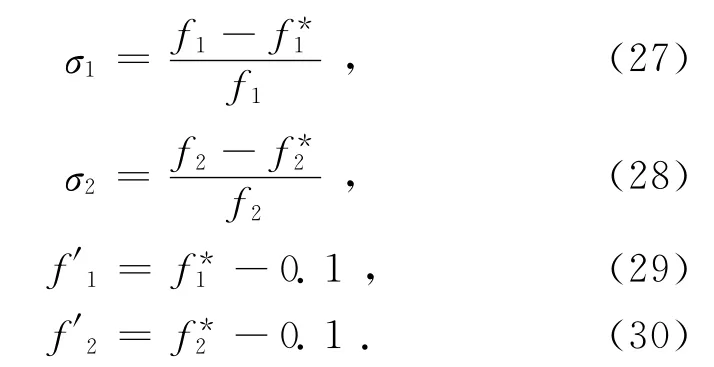
步骤5:根据决策者偏好,设定两个优化目标的权重系数为λ1和λ2,且λ1+λ2=1。
步骤6:采用字典式赋权切比雪夫方法,引入参数ε,并将原多目标模型转化为以下单目标模型

式(6)及式(9)~式(30)执行以上约束条件。
步骤7:求解上述单目标模型,其获得的最优解即为原多目标模型最优解。
步骤8:输出优化方案。
4 算 例
为验证模型和算法的有效性,设计4个不同规模的测试算例,且算例的网络节点由MATLAB在30km×30km的区域内随机生成。各算例节点数量(产生点,回收点的建设候选点,加工点的建设候选点,处置点的建设候选点)分别为:小规模的基础算例(15,5,5,5),中规模的拓展算例(30,5,5,5)和(60,10,10,10),大规模的拓展算例(120,20,20,20)。其中,基础算例是后续算例的拓展基础,主要验证模型和算法的有效性,分析成本-风险变化曲线;拓展算例则进一步验证模型和算法的有效性,并分析参数鲁棒性。
设定φ=25%,θ=65%,δ=70%,可回收、可加工和可处置废物单位运输成本分别为100元/t/km,150元/t/km 和 250 元/t/km;地面纵 向 风速 为3m/s;设定传播时刻集合为{5,10,15,20,25,30};其他参数随机设定。采用CPLEX12.6求解,各优化参数设置为默认值,所有计算在CPU为Interl Core i7-2400 3.10GHz,RAM 为8.00GB及操作系统为 Windows 10~64Bits的个人电脑上执行。
4.1 基础算例
如图4所示,基础算例中含有产生点15个(节点1~15),回收、加工以及处置的建设候选点各5个(节点16~20)。各建设候选点的人口密度分别为2.2人/m2、0.8 人/m2、1.5 人/m2、0.6 人/m2及1.7人/m2,各类设施建设成本和最大能力如表1所示。
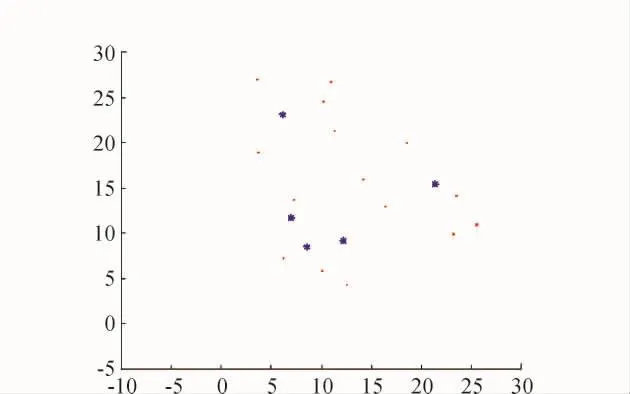
图4 产生点与各个运输节点位置分布
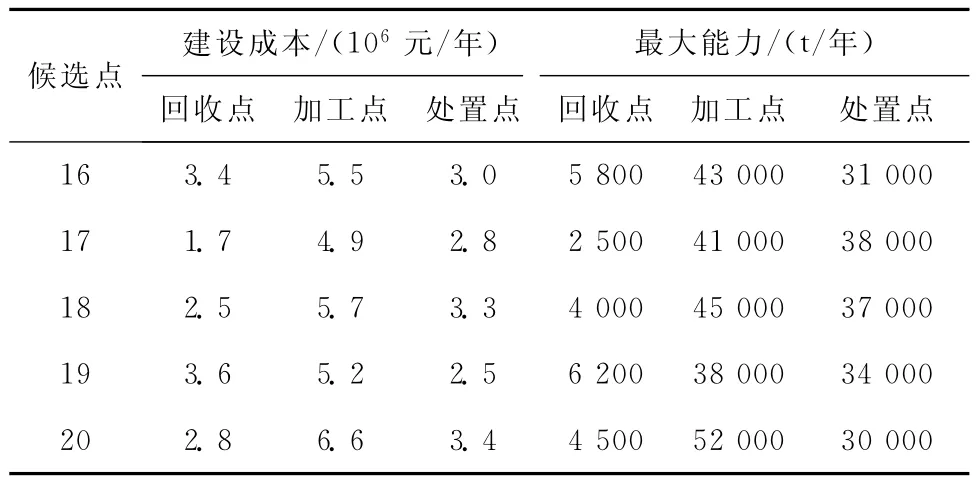
表1 设施建设候选点信息
令各设施的建设数量分别为2,依次求解总风险最小和总成本最小的单目标优化问题,在5s内求得总风险和总成本值为2 002.334元和2 002.114×105元。依据决策者的偏好,将λ1以0.05的增幅从0变化到1,其成本-风险变化趋势如图5所示。由此可见,本文构建的模型和算法能够为决策者提供多个有效决策,其中,当λ1=[0.35,0.95]时的优化结果较为稳定。受新冠疫情下医疗废物处理的可弱化成本影响,本文加大风险防控力度,主要推荐λ1=0.70的优化方案:回收点和加工点建设位置为节点19,处置点建设位置为节点17和19,其运量分配结果如表2所示。该优化方案的总成本2 112.144×105元,总风险2 011.719元,相较总成本最小的单目标优化方案,总风险降低了29.07%;相较于总风险最小的优化方案,总成本减少了10.20%。

图5 不同权重系数下选址-分配方案的成本-风险变化

表2 基础算例(15,5,5,5)的运量分配方案(λ1=0.70)
采用同样的参数,可将最终传播时间设定为20min,分别对比分析“暴露人口吨数”模型与新风险模型的优化结果,以及非时变和时变“环境-人口”风险模型的优化结果。如表3所示,相较于“暴露人口吨数”的风险模型,考虑了时变“环境-人口”风险的优化方案可减少总成本5.38%;相较于非时变“环境-人口”风险模型,考虑了时变条件的优化结果可降低4.43%的总成本。

表3 计算结果对比1
4.2 拓展算例
为进一步验证模型和算法的有效性,并分析参数的鲁棒性,在基础算例之上随机新增节点,拓展生成3个中大规模算例。如表4所示,新模型和算法在30s内可为拓展算例提供多个有效方案。以λ1=0.70时的最优解为基础,分别将算例(30,5,5,5)和(60,10,10,10)中回收点的最大能力扩大10倍,其最优方案对比结果如表5所示。当两个算例的回收点最大能力扩大后,建设成本较小和人口密度较小的候选点优先等级得到提升,使得总成本分别降低79.60%和5.52%,总风险分别减少29.36%和36.08%。

表4 计算结果对比2
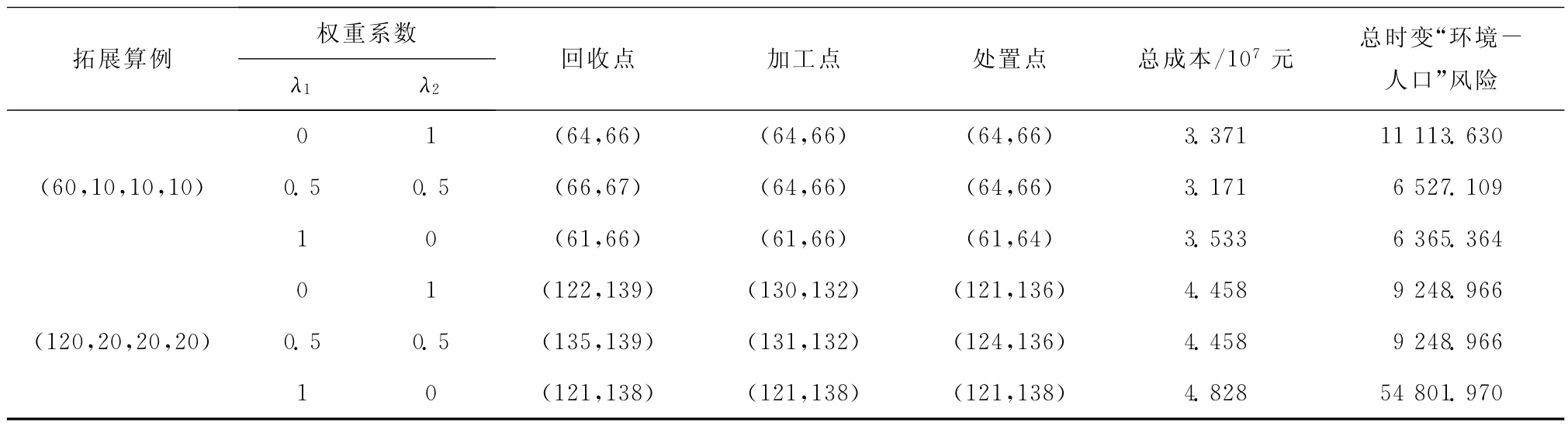
续表4

表5 计算结果对比3
5 结 论
为联合降低环境污染和人员感染,本文提出了重大疫情下医疗废物的多目标选址-分配模型和求解方法,同时确定了医疗废物回收点、加工点及处置点的建设位置,分配了产生点和各设施节点之间的医疗废物运输量。
1)根据新冠病毒对环境系统的依附性,以及环境系统的动态变化,设计了时变“环境-人口”风险度量方法;
2)建立了总时变“环境-人口”风险最小和总成本最小的多目标优化模型;
3)基于字典式赋权切比雪夫方法设计了多目标优化算法;
4)以4个不同规模的测试算例验证了模型和算法的有效性及参数鲁棒性,计算结果表明:新模型和算法能够依据决策者偏好提供多个有效优化方案;相较于传统方法,新模型和方法的优化结果能够有效减少成本(平均约27.27%)和二次传染风险(平均约32.72%)。
