多并联机构布局优化分析

王玉甲，王璐，唐宝富，徐文华

(1.哈尔滨工程大学 机电工程学院，黑龙江 哈尔滨 150001； 2.南京电子技术研究所，江苏 南京 210039)

随着阵面向大尺寸、轻薄化的方向发展，对其平面度的需求也不断提高，传统的支撑控制方式难以满足其需求[1]。考虑到并联机构具有位置误差不会积累、刚度大、支撑面积大以及承载能力强的优点[2]，并且由于阵面尺寸相对较大，为尽量减小阵面的平面度，本文采用多组并联机构支撑阵面，而多并联机构的布局对阵面的变形有较大的影响，因此研究多并联机构的布局优化方法具有重要的研究意义和实用价值。

目前国内外对于布局优化的研究主要集中在薄壁件的装夹布局优化领域，而对于多并联机构布局优化的研究则很少涉及，本文阐述薄壁件装夹布局优化的研究现状以供参考和借鉴。文献[3]通过不断改变薄壁件定位元件的位置，利用有限元方法得到其装夹变形，最终得到最小装夹变形对应的位置。文献[4]以装夹变形最小为目标函数建立最优化模型，并基于遗传算法进行了最优布局的解算。文献[5]建立了薄壁件装夹变形的有限元模型，并以此分析定位元件位置等因素与装夹变形量之间的关系。文献[6]将有限元法和遗传算法结合，以减小薄壁件的变形量为目标，对装夹布局进行优化。文献[7]以航空框类的铣削过程为研究对象，建立优化模型，利用遗传算法对装夹元件的数量和布局进行优化分析，并使用有限元软件计算加工变形量，得到最优装夹布局。

在以上的研究中，由于装夹元件具有较小的结构尺寸，因此，可将其视为点支撑以开展分析计算，而在进行多并联机构的布局优化时，由于其支撑面积较大，无法视为点支撑，并且并联机构与阵面之间通过螺栓固定连接，阵面属于刚柔耦合体，其变形情况非常复杂，很难通过传统的布局优化方法进行求解；此外在这些研究中当采用最优化理论进行布局优化分析时，最优化模型的目标函数通常为工件的最大变形量，而工件的最大变形量只能反映其局部变形情况，因此求解得到的最优布局对应的阵面的整体变形情况不一定很好。

本文在采用基于有限元的布局优化方法进行最优布局的求解时发现该方法求解效率低下，当阵面尺寸较大时，并联机构不同支撑布局的数目将会大大增加，求解时间将会很长。

因此，针对非点支撑结构、目标函数选择及求解效率低下的问题，本文对支撑面积相对较大的多并联机构布局优化问题开展研究，并以阵面平面度最小为优化目标，研究多元非线性回归和遗传算法相结合的布局优化方法，以提高计算效率。

1 基于有限元方法的布局优化

由于传统的布局优化方法很难求解并联机构支撑面积较大且阵面为刚柔耦合体的情况，而有限元方法非常适合用于这种变形情况复杂的场合，因此本文采用有限元方法解决多并联机构的布局优化问题。

1.1 布局优化模型的建立

本文以2 000 mm×2 000 mm×5 mm(长×宽×高)的矩形阵面和支撑面长宽均为450 mm的4 组(通过“N-2-1”准则确定)并联机构为例，将并联机构与阵面边线的距离设置为参数化变量，建立了阵面和多并联机构的参数化模型，如图1所示。

图1 阵面和多并联机构的参数化模型Fig.1 Parametric models of plane and multiple parallel mechanisms

基于最优化理论，优化模型的建立就是确定目标函数、设计变量及其约束条件。传统的布局优化方法在建立最优化模型时其目标函数通常为工件的最大变形量，但最大变形量只能反映阵面的局部变形情况，不能很好地描述阵面的整体变形情况。而平面度是阵面具有的宏观凹凸高度相对理想平面的偏差，可用来描述阵面整体的变形情况，因此，可以将被支撑平面的平面度最小作为多组并联机构支撑布局优化的目标，以平面度为目标函数开展多组并联机构的布局优化模型研究。

阵面的平面度误差可以通过吻合精度，即阵面上多个采样点挠度的均方根(root mean square，RMS)来表达，因此，以阵面的RMS值作为本文优化布局模型的目标函数[8]；约束条件为各并联机构的支撑位置不重叠并且并联机构的动平台不能超出大型阵面的边界；设计变量为并联机构与大型阵面边线的距离。

本文建立的支撑大型阵面的多并联机构的布局优化模型为：

(1)

式中：F(X)为目标函数，即RMS；X为设计变量；Xd、Xu为X的下限值和上限值。

1.2 布局优化的分析计算

本文利用ANSYS Workbench进行多并联机构布局优化分析，基于单目标自适应优化方法(adaptive single objective,ASO)，通过迭代求解，得到对应阵面平面度最小值的多组并联机构的最优布局。

基于前述建立的参数化模型，首先进行用于平面度采样点的选择，考虑到阵面结构对称性、尺度大小及其刚度影响，均匀选取阵面上的49个采样点进行分析(如图1所示)。针对本文设计的4 组并联机构，可知共有8 个设计变量，考虑到支撑的对称性及机构不能干涉，选择并联机构的支撑位置距阵面边线的距离范围为0～550 mm，布局优化过程的初始值为200 mm。

在进行布局优化计算时，考虑速度和成本等因素，本文设置样本数为45 组((n+1)(n+2)/2，n为设计变量个数)，生成初始样本后，分别计算其对应的RMS，并面向平面度最小，完成迭代计算。考虑仿真总时长，本文指定迭代8次，每次45个样本，共计计算360 次，输入变量缩减域的数目为8[9]。

通过布局优化迭代计算，得到阵面的平面度和并联机构支撑位置的变化趋势如图2所示。可见，阵面的平面度渐进收敛至最小值，各并联机构的支撑位置也逐渐收敛。

最优布局计算结果如图3所示。

经过ANSYS Workbench计算给出了3组多并联支撑机构的最优布局候选点，平面度均小于1 mm，满足使用要求。

最优布局1的阵面RMS为2.058 8×10-5m(0.020 588 mm)，支撑位置为162.36 mm。通常，考虑到加工精度及安装方便，一般要对计算值进行圆整处理，得到最优支撑位置。根据计算结果，本文将并联机构中心点到阵面边线的距离设定为390 mm，即圆整后选支撑位置为165 mm。此时，对应的阵面RMS仍为最小。

图2 目标函数与设计变量变化趋势Fig.2 Trend chart of target function and design variables

图3 最优布局Fig.3 Optimal layout

1.3 最优布局与均匀布局结果对比

为了验证本文优化布局方法的有效性，在ANSYS Workbench中求解均匀布局下阵面的平面度值，并进行对比分析，结果如表1所示。

表1 最优布局与均匀布局结果对比

并联机构的2种布局形式结果不同，但差异不大。最优布局情况下的RMS约为0.020 59 mm，而均匀布局情况下，即并联机构中心点距离阵面边线500 mm时，阵面的RMS约为0.022 52 mm，二者相差0.001 93 mm，最优布局相较于均匀布局，RMS值减小了8.57%，说明本文对并联机构进行优化布局的有效性。但由于本文研究的阵面尺度较小，支撑机构数目较少且可变动的范围也较小，优化布局方法对平面度RMS的改善并不显著。

2 不同目标函数求解结果对比

为了验证以阵面平面度最小为目标的最优布局方法的有效性，本文也对以阵面的最大变形量为目标函数的布局优化方法进行研究，并对比分析2种目标函数对优化结果的影响。

由于平面度表示的是阵面与理想平面之间的偏差，能够很好地描述阵面整体的变形情况，因此仍以阵面的RMS为评价指标对2种目标函数表示方式进行评价。2种方式所求结果如表2所示。

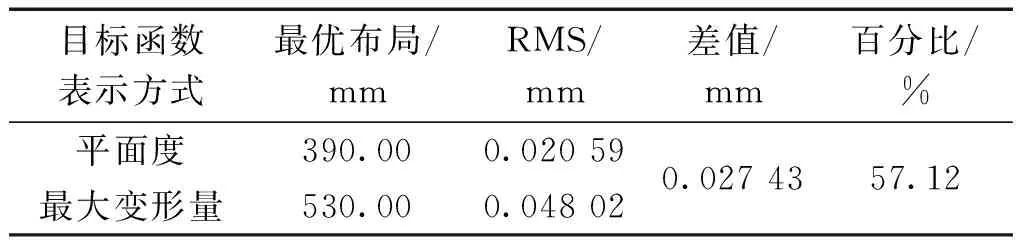
表2 不同目标函数求解结果对比

由表2可知，当以阵面的平面度值为目标函数时，其最优布局为并联机构中心点距离阵面边线390 mm，对应的阵面的RMS值约为0.020 59 mm；当以阵面的最大变形量为目标函数时，其最优布局为并联机构中心点距离阵面边线530 mm，阵面的RMS值约为0.048 02 mm。2种目标函数表示方式的RMS差值为0.027 43 mm，以平面度为目标函数的方式相比于以最大变形量为目标函数的方式，其RMS值减小了57.12%，说明以平面度为目标函数求得的最优布局对应的阵面整体变形情况要更好，从而验证了以平面度为目标函数的多并联支撑机构布局优化方法的有效性。

3 基于多元非线性回归和遗传算法的布局优化

本文在研究基于ANSYS Workbench有限元分析的布局优化方法时发现其计算时间非常长。为了降低布局优化计算时间，提高计算效率，本文将多元非线性回归理论和遗传算法相结合，研究更加高效的多并联机构布局优化方法。

3.1 多元非线性回归模型的建立与验证

本文首先基于有限元结果建立多并联机构支撑位置和阵面的平面度的多元非线性回归模型，再对模型的相关性和显著性进行检验。

本文方法是根据有限元技术建立阵面平面度与并联机构支撑位置的预测模型，便于求解不同支撑布局下阵面的平面度值，避免了漫长的有限元分析的过程，随后采用遗传算法求解最优解，提高求解最优布局的效率。

针对本文给出的阵面实例，考虑其对称性，在计算中做一定程度的简化，设定并联机构按阵面的2条中心对称布置，将求解4组并联机构布局问题简化为求解一个并联机构支撑位置的问题。并联机构的布局如图4所示。

图4 并联机构布局示意Fig.4 Schematic diagram of parallel mechanism layout

本文以离散化的单个并联机构的支撑位置(x，y)为自变量(范围：225,230,…,775 mm)，以阵面的RMS为因变量，设计实验方案。基于有限元方法计算得到不同布局下阵面的RMS值，得到36组多元非线性回归样本数据如表3所示。

表3 多元非线性样本数据Table 3 Multivariate nonlinear sample data mm

使用1stOpt软件对表3中的样本数据进行拟合。通过基于麦夸特法(Levenberg-Marquardt)和通用全局优化法的迭代计算，在31代后达到收敛标准，得到待定多项式系数的近似解，以及并联机构支撑位置x、y和阵面平面度f(x，y)之间的多元非线性回归方程[10]：

f(x,y)=0.457 7-0.001 3x-0.001 1y+
1.537 1×10-6x2+4.782 8×10-7xy+
1.261 9×10-6y2

(2)

为了分析该方程的拟合效果，需要其进行相关性检验，计算得到其自变量和因变量之间的相关系数|R|=0.945 8，结果接近于1，说明方程的拟合效果很好。

在显著性检查中，设定显著水平α为0.05，并由前述方案可得，在样本数n为36，自由度数(即自变量个数)p为2时，Fβ(p,n-p-1)为3.32，回归计算的F值为288.81。由于F≥Fβ，因此在给定的显著性水平下，上述方程线性回归显著。

综上，本文获得的预测模型具有很好的拟合效果，可以用来表达并联机构支撑位置和阵面平面度之间的关系。

3.2 耦合优化模型的建立

基于上述的多元非线性回归方程，建立阵面平面度和多并联机构支撑位置的耦合优化模型，并为应用遗传算法进行布局优化分析提供前提。

耦合优化模型中，将并联机构的支撑位置X=[x1,x2，…,xm]作为设计变量，将阵面的平面度预测值f(X)作为目标函数，将阵面上采样点的挠度值ω作为状态变量，ω既是X的函数，也是f(X)的重要参数；耦合优化模型的约束条件与前述分析相同。模型表达式(3)为：

(3)

3.3 布局优化计算

本文基于遗传算法进行多并联机构的布局优化分析，求解得到最优布局。各代种群中最优解的分布位置的散点图如图5所示。

图5 各代种群最优解分布位置Fig.5 Distribution location map of optimal solutions for generation population

由图5可见，在(380 mm，380 mm)附近，并联机构支撑位置最优解分布较为集中，少数最优解分布较分散，其原因是在初始迭代过程中，最优解及其支撑位置还未收敛，离散性较大，随着迭代次数增加，最优解对应的支撑位置逐渐收敛于380 mm附近区域。

在每一代种群中，各个体对应的支撑位置也各不相同，最后一代种群所有个体的分布位置散点图如图6所示。可见，同一代种群中，大多数个体对应的支撑位置的分布也主要集中在某一区域，同时也存在一些个体对应的支撑位置分布在较离散的区域，这也反映了种群中个体多样性，有利于代间遗传。

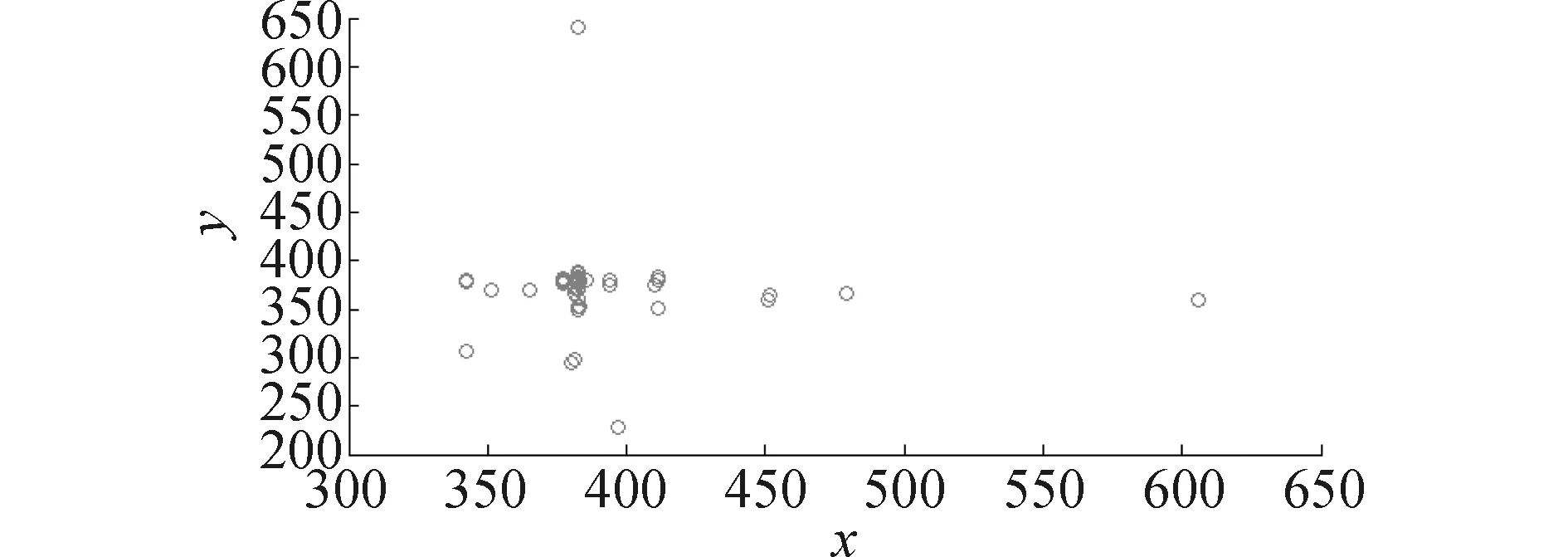
图6 最后一代种群个体分布Fig.6 Individual distribution map of the last generation population

遗传过程中，各代种群的目标函数的最小值如图7所示。从图中可见，在遗传20代左右，目标函数即平面度收敛到最小值0.009 678 mm，获得最优解。

图7 目标函数最小值随遗传代数变化曲线Fig.7 Change diagram of population objective function and genetic algebra

遗传过程中，每一代种群的个体目标函数平均值如图8所示。从图中可见，在遗传20代左右以后，目标函数平均值在0.013 mm上下波动，说明多数个体在种群内的分布集中性较好，同时，波动范围趋于平稳，也说明了种群内个体任然具有一定的多样性。

图8 种群中个体目标函数平均值曲线Fig.8 Diagram of average value of individual objective function in population

综上，基于遗传算法结果，经过最优解的圆整，可得并联机构的最优支撑位置为(380 mm，380 mm)，阵面的平面度值约为0.009 678 mm。

3.4 2种布局优化方法的对比分析及应用

针对多并联机构的布局优化问题，本文分别研究了采用有限元软件的布局优化方法和基于多元非线性回归和遗传算法相结合的布局优化方法，并针对给定尺寸的阵面完成了布局优化分析，现对以上2种方法进行对比，结果如表4所示。

表4 2种布局优化方法的对比

由表4可知，基于有限元的布局优化方法求解时间长达10 h，其最优布局为并联机构距离阵面边线390 mm；而基于多元非线性回归和遗传算法的布局优化方法求解时间仅为1 min，其最优布局为并联机构距离阵面边线380 mm。

基于前述计算结果可知，布局结果在最优解附近相差10 mm，阵面平面度相差极小，可以满足给定的技术要求，同时，在支撑范围变化量为550 mm的前提下，该差值相对于变化范围的百分比约为1.8%，可以认为2种求解方法结果接近。进一步验证了本文所研究的基于多元非线性回归和遗传算法的方法的快速性和准确性。

基于以上分析，本文给出如下建议：

1)对于阵面尺度较大、形状规则(如对称结构)、支撑机构数量确定的情况，可采用基于多元非线性回归和遗传算法的布局优化方法。

2)对于阵面尺度较小、形状不规则、并联机构数量不确定的情况，可采用基于有限元软件的布局优化方法。

4 结论

1)本文在ANSYS Workbench中使用基于迭代的单目标优化方法，通过改变各并联机构的支撑位置进行优化分析，求得的最优布局为并联机构距离阵面边线390 mm，对应的阵面最小平面度值约为0.020 59 mm，满足了技术指标中1 mm的平面度要求。与均匀布局相比，阵面的平面度值减小了8.57%。

2)本文以阵面最大变形量为目标函数进行了布局优化分析，求得的最优布局为并联机构距离阵面边线530 mm，其对应的阵面平面度值约为0.048 02 mm，2种目标函数表示方式的最优布局对应的阵面平面度值相差0.027 43 mm，以阵面平面度值为目标函数的方式与该方式相比，其RMS值减小了57.12%。

3)针对有限元方法求解时间过长的情况，本文研究了基于多元非线性回归和遗传算法的布局优化求解方法，求得的并联机构的最优支撑位置距离阵面边线380 mm，与有限元方法的得到的距离相差10 mm，其相对于距离变化范围的百分比约为1.8%，且2种方法所求平面度结果非常接近。而该方法求解时长约1 min，远小于有限元方法的10 h，验证了该方法的有效性。