桁架结构弹塑性屈曲承载力计算方法
2020-11-19张明谷任奇童万波
张明,谷任奇,童万波
(1.东南大学 混凝土与预应力混凝土结构教育部重点实验室,江苏 南京 210018; 2.中铁二院工程集团有限责任公司,四川 成都 610031; 3.西南交通大学 土木工程学院,四川 成都 610031)
桁架结构因其特殊的结构形式,其杆件主要受轴向拉力或压力,能充分发挥结构材料的作用,减轻结构的自重,故而在工程实际中得到了广泛的应用[1-2]。而一般钢构件的长细比较大,故桁架结构稳定问题是桁架结构工程应用中面临的一个主要问题,同时很多学者对桁架结构的稳定性问题作了大量的研究分析[3-10]。孙焕纯等[3]通过对桁架结构屈曲稳定性理论进行讨论,提出了桁架结构线弹性屈曲承载力的计算方法。柯秋鸿等[4]对无支撑和有支撑的2种立体桁架结构体系进行了线弹性屈曲承载力分析。郭彦霖等[5]针对钢管桁架拱平面内的弹性屈曲进行了分析。乐慈等[6]结合天津梅江会展中心工程,对张玄桁架结构的线性屈曲承载力进行了分析。杜兆宇[7]应用ABAQUS有限元软件对某悬挑双向折形斜交平面桁架结构进行了线弹性屈曲承载力分析。侯亚委等[8]对某电厂大跨度干煤棚钢结构进行了线性特征值屈曲分析。Dou等[9]对圆钢管桁架拱结构采用静态平衡法,研究分析了的圆钢管桁架拱结构弹性面外屈曲荷载。Madah等[10]基于梯度的移动渐近线方法,在考虑几何缺陷的情况下利用共旋转梁方程探讨了结构的局部屈曲和桁架的整体屈曲问题。
然而,目前学者只研究了桁架结构的线弹性屈曲承载力或者弹性屈曲承载力,少有研究桁架结构的弹塑性屈曲承载力。本文提出一种通过确定桁架结构最不利杆件,同时计算桁架结构最不利杆件的弹塑性屈曲承载力,来分析桁架结构弹塑性屈曲承载力的计算方法。并且本文通过应用本方法对单杆结构以及简单桁架结构在静力荷载作用下的弹塑性屈曲承载力分析以及简单桁架结构动力荷载作用下的弹塑性屈曲承载力分析,同时与有限元软件ABAQUS分析的屈曲承载力进行对比,以验证本文提出方法的正确性与可行性。
1 桁架弹塑性屈曲承载力分析方法
1.1 确定最不利杆件
对桁架结构进行弹塑性屈曲承载力分析,其首要任务是找到桁架结构在其已知荷载状况下的最不利受压杆件。因为,最不利杆件是桁架结构在该荷载状况下最早发生屈曲的杆件,进而可能导致整个桁架结构的屈曲破坏。确定最不利杆件需对桁架结构进行线弹性分析[11]:
K·D=P
(1)
式中:K为桁架结构线弹性刚度矩阵;P为桁架结构在该荷载状况下的荷载向量;D为桁架结构在荷载向量P作用下,桁架结构的位移向量。
桁架结构各杆件在荷载P作用下的应力σi可根据线弹性分析结果及式(2)确定[11]:
(2)
式中:σi为桁架结构第i根杆件的应力;Ni为桁架结构第i根杆件的轴向力;Ai为桁架结构受压区第i根杆件的横截面面积。根据式(2),将桁架结构中压应力最大的杆件定义桁架结构在该荷载状况下的最不利杆件。在此基础上,定义最不利杆件在该荷载状况下的轴向力为N0,荷载向量P为参考荷载P。
1.2 最不利杆件与桁架结构的关系
桁架结构最不利杆件的确定是综合考虑了结构的布置形式、荷载分布、杆件与节点之间的连接以及材料非线性,这些因素体现在1.1节中最不利杆件的确定及1.3节中最不利杆件线弹性屈曲承载力计算部分。因此,桁架结构最不利杆件是桁架结构中的关键构件,因为最不利杆件的屈曲可能会导致桁架结构的局部屈曲,进而可能引起结构连续倒塌,甚至引起整个结构的倒塌。同时,结构的破坏是由于结构杆件破坏逐渐积累导致。综上所述,可以将最不利杆件的屈曲承载力作为分析桁架结构屈曲承载力的重要参考指标,即可通过参考杆件的屈曲承载力估算桁架结构屈曲承载力的下限值。
1.3 最不利杆件线弹性屈曲承载力计算
根据结构力学中稳定计算理论[11],桁架结构最不利杆件的线弹性屈曲承载力可表示为:
(K-S)Δ=0
(3)
S=Ples
(4)
式中:K为桁架结构最不利杆件的线弹性刚度矩阵;S为桁架结构最不利杆件在线弹性屈曲承载力作用下的几何刚度矩阵;Ple为桁架结构最不利杆件的线弹性屈曲承载力;s为杆件单元的几何刚度矩阵;Δ为桁架结构最不利杆件在其线弹性屈曲承载力作用下的位移向量。因此,桁架结构最不利杆件的线弹性屈曲承载力Ple为:
|K-Ple·s|=0
(5)
1.4 最不利杆件弹塑性屈曲承载力计算
计算得到桁架结构最不利杆件线弹性屈曲承载力Ple后,简单桁架结构最不利杆件的弹塑性屈曲承载力Pcr_R即可根据Dunkerley提出的压杆强度曲线[12-14]计算得到:
(6)
(7)
Ny=fyA
(8)
式中:Ny为桁架结构最不利杆件的屈服承载力,可根据式(8)计算;Λ为最不利杆件的广义长细比[12];其中fy为最不利杆件材料的屈服应力,A为最不利杆件的横截面面积。
1.5 桁架结构弹塑性屈曲承载力计
计算得到简单桁架结构最不利杆件的屈曲承载力Pcr_R后,根据式(9)和式(10)可得到桁架结构的弹塑性屈曲承载力[12]。
Pcr=λP
(9)
λ=Pcr_R/N0
(10)
式中:Pcr为桁架结构的弹塑性屈曲承载力;λ为桁架结构弹塑性屈曲承载力的比例因子;P为桁架结构的参考荷载。
2 有限元模拟方法及模型建立
桁架结构有限元模拟分析的屈曲承载力是通过采用有限元软件ABAQUS进行模拟分析。桁架结构模型中各杆件均采用ABAQUS中B31单元进行模拟,模型节点均采用固结;采用2种方法进行对比分析:特征值屈曲分析方法和riks分析方法,模型网格划分方式采用自由网格划分。
梁单元B31的几何图如图1所示,其假定:构件的变形可以由沿长度变化的位移函数确定,并且适合于以剪切变形为主的构件建模,如深梁和细长梁进行建模。梁单元B31在每个节点处具有6个自由度:沿x向、y向以及z向的平移,以及关于x轴、y轴以及z轴的旋转[15]。
本文所选的桁架结构模型为单杆结构模型和单层单跨结构模型,其结构布置及荷载分布如图2所示。桁架结构采用材料为低碳钢Q345,其弹性模量E为206 GPa,屈服强度σy为354 N/mm2,钢材泊松比ν为0.3,各杆件杆长l为2 m,杆件截面尺寸为
Φ100 mm× 5 mm。钢材Q345材料性质假定为理想弹塑性,其应力-应变曲线如图3所示。
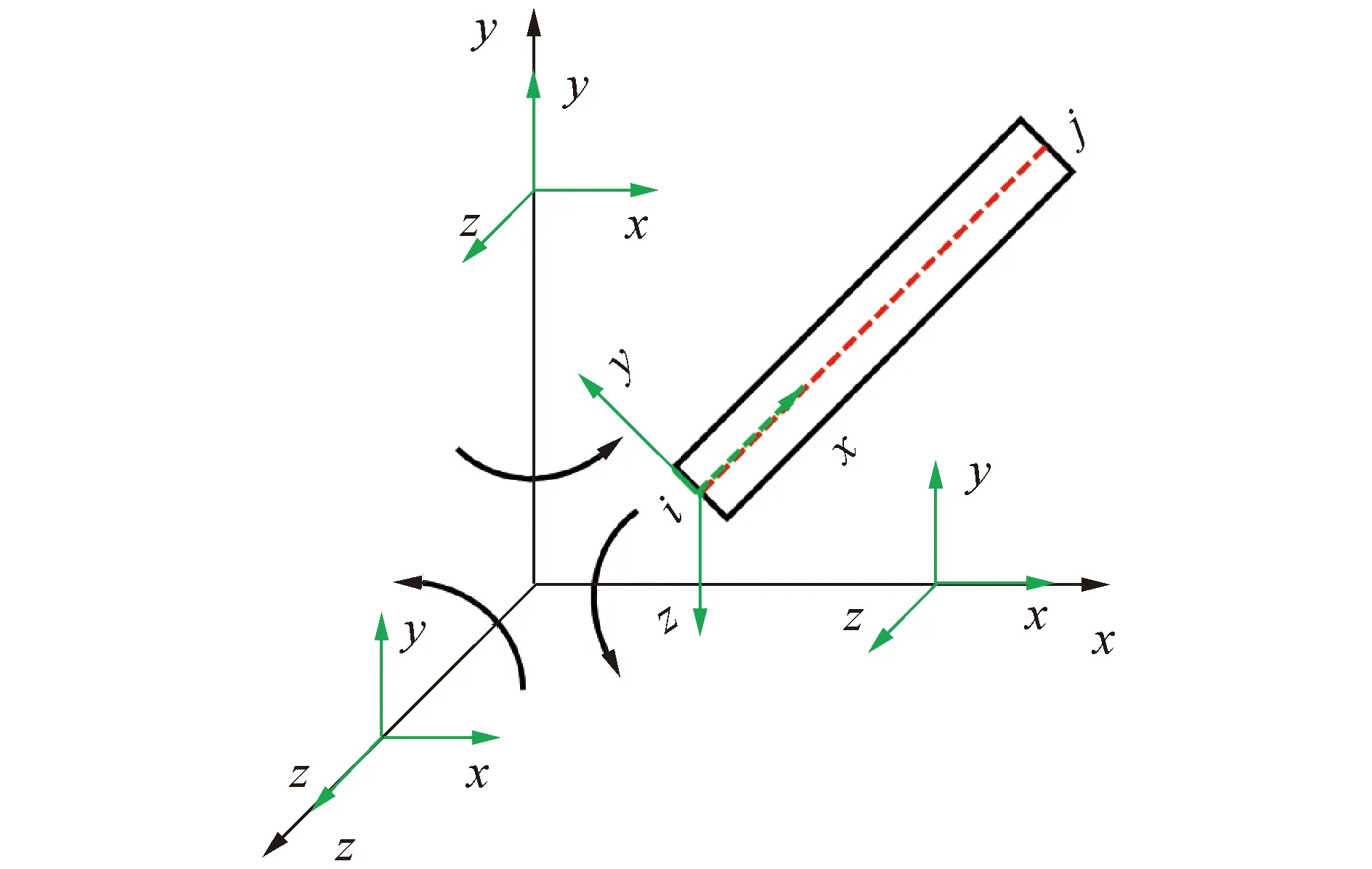
图1 B31单元几何图[15]Fig.1 The geometry of element B31[15]
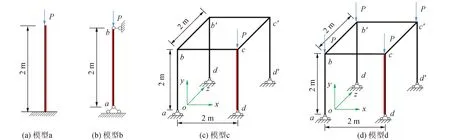
图2 简单桁架结构边界、布置及荷载分布Fig.2 The boundary, configuration and the load of the simple truss
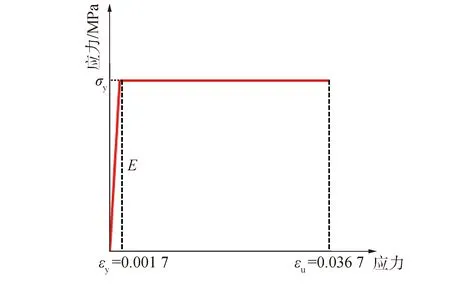
图3 钢材应力-应变曲线Fig.3 The stress-strain curve of the steel
3 桁架结构弹塑性屈曲承载力分析
3.1 桁架结构弹塑性屈曲承载力计算
3.1.1 结构最不利杆件的确定
为了便于分析,对所有分析的桁架结构模型的荷载P的大小均假设为单位荷载1 N。为确定桁架结构模型的最不利杆件,可利用有限元软件ABAQUS对桁架结构模型a、模型b、模型c和模型d分别进行线弹性分析。根据有限元分析结果,桁架结构模型a、模型b、模型c和模型d的最不利杆件为图2中杆件cd。桁架结构模型a、模型b、模型c和模型d的最不利杆件在荷载P作用下的轴向力N0及参考荷载P见表1。
3.1.2 最不利杆件线弹性屈曲承载力分析
根据结构力学中结构稳定计算理论[11],简单桁架结构模型a、模型b、模型c和模型d的最不利杆件的弹性刚度矩阵K和单元几何刚度矩阵s见表2。因此,根据式(5)可分别计算得到桁架结构模型a、模型b、模型c和模型d的最不利杆件的线弹性屈曲承载力,计算结构见表3。

表1 最不利杆件轴向力及参考荷载

表2 桁架结构模型最不利杆件K和s

表3 桁架结构最不利杆件线弹性屈曲承载力
3.1.3 最不利杆件弹塑性屈曲承载力分析
在根据式(5)计算得到桁架结构最不利杆件的线弹性屈曲承载力Ple后,根据式(6)即可计算得到桁架结构最不利杆件的弹塑性屈曲承载力Pcr_R,具体相关参数的计算及结果见表4。
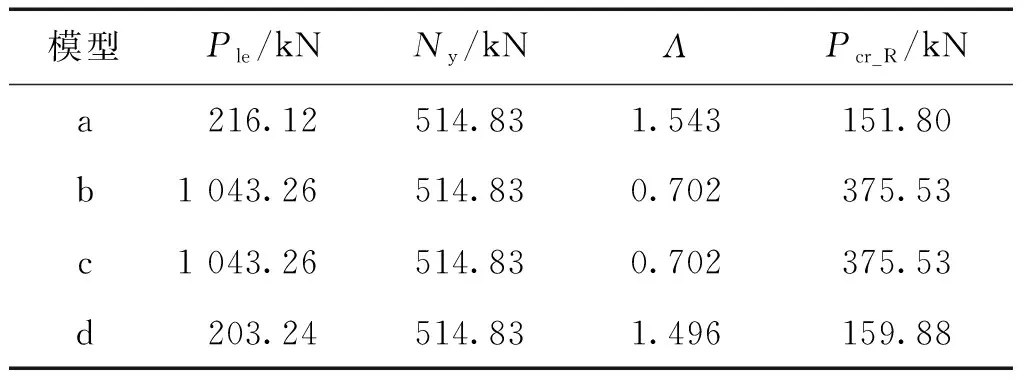
表4 桁架结构最不利杆件弹塑性屈曲承载力
3.1.4 桁架结构弹塑性屈曲承载力分析
根据式(6)计算得到桁架结构最不利杆件的弹塑性屈曲承载力Pcr_R后,桁架结构的弹塑性屈曲承载力Pcr即可根据式(9)和式(10)计算得到,其具体相关参数的计算及结果见表5。
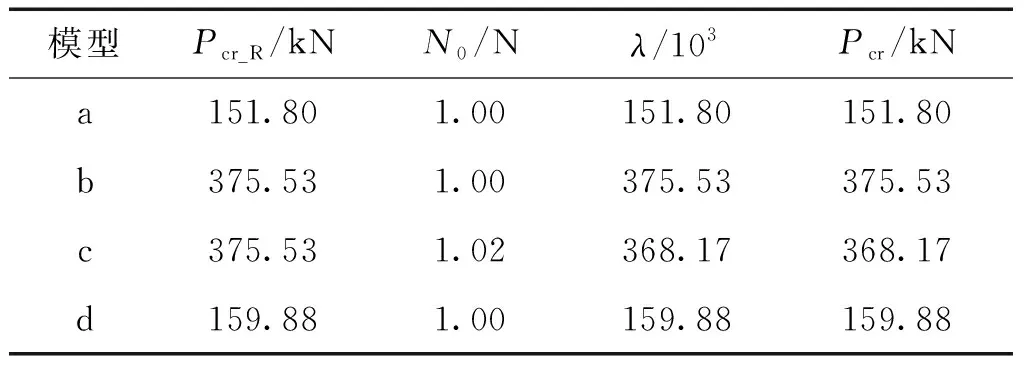
表5 桁架结构弹塑性屈曲承载力
4 桁架屈曲承载力有限元模拟分析
桁架结构模型a、模型b、模型c以及模型d应用有限元软件ABAQUS特征值屈曲分析方法分析得到的桁架结构屈曲承载力Pcr(B)和应用riks分析方法得到的桁架结构屈曲承载力Pcr(R)见表6。为便于对比分析,表中还给出了基于最不利杆件桁架结构的弹塑性屈曲承载力估算值Pcr。另外,桁架结构模型a、模型b、模型c以及模型d应用特征值屈曲分析得到的位移云图和应用riks分析得到的位移云图分别如图4和图5所示。桁架结构模型a、模型b、模型c以及模型d应用riks分析方法的荷载加载曲线如图6所示。
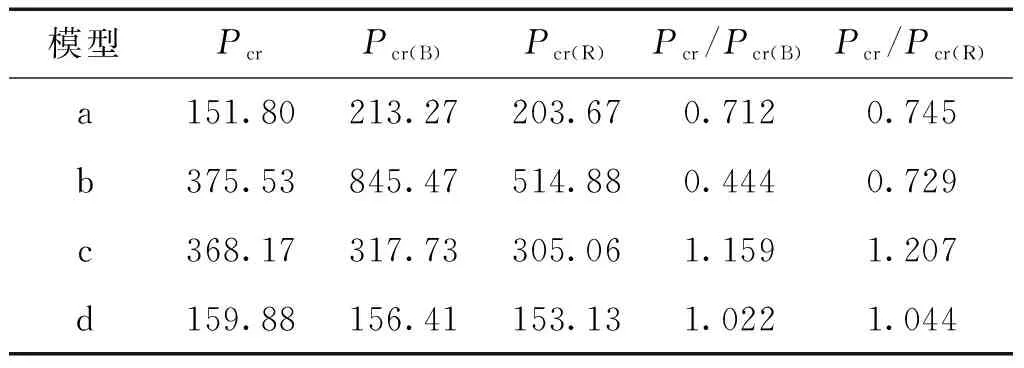
表6 桁架结构屈曲承载力Table 6 The buckling strength of truss structure
从表6中可见,桁架结构模型a、c和模型d根据本文给出的方法计算的弹塑性屈曲承载力与应用有限元软件ABAQUS特征值屈曲分析方法和riks分析方法得到的屈曲承载力较为接近。由于特征值屈曲分析是假定结构在整个分析过程中均为弹性(未考虑材料的塑性),桁架结构模型b在荷载达到在弹性屈曲荷载前,结构已经发生强度破坏,故基于本文方法估算的桁架模型b的弹塑性屈曲承载力与有限元软件ABAQUS特征值屈曲分析方法得到的屈曲承载力相差较大。而riks分析的结果更接近压溃荷载,其与基于最不利杆件方法估算的桁架结构屈曲承载力较为接近。
研究发现,当构件长细比较大时,结构失效以屈曲破坏为主,此时基于最不利杆件方法估算的桁架屈曲承载力与利用特征值屈曲分析所获得的屈曲承载力较为接近;当构件的长细比较小时,构件以强度破坏为主,此时基于最不利杆件方法估算的桁架结构屈曲承载力与利用riks分析结果较为接近。

图4 桁架结构特征值分析位移云图Fig.4 The displacement cloud map of simple truss analyzed by eigenvalue analysis
对比桁架结构模型a、模型b、模型c以及模型d应用特征值屈曲分析得到的位移云图和应用riks分析得到的位移云图,由于2中分析方法的原理不同,故在模型屈曲破坏时的破坏形态并不相同,但分析得到的模型屈曲承载力较为接近,也与本文所提方法计算桁架结构弹塑性屈曲承载力较为接近。结合图5中桁架结构模型b应用riks分析得到的位移云图和图6中桁架结构荷载加载曲线,可发现桁架结构模型b的破坏形态更接近杆件的受压强度破坏。同时,从图6可看出,桁架结构模型a、模型c和模型d的破坏形态以屈曲破坏为主。
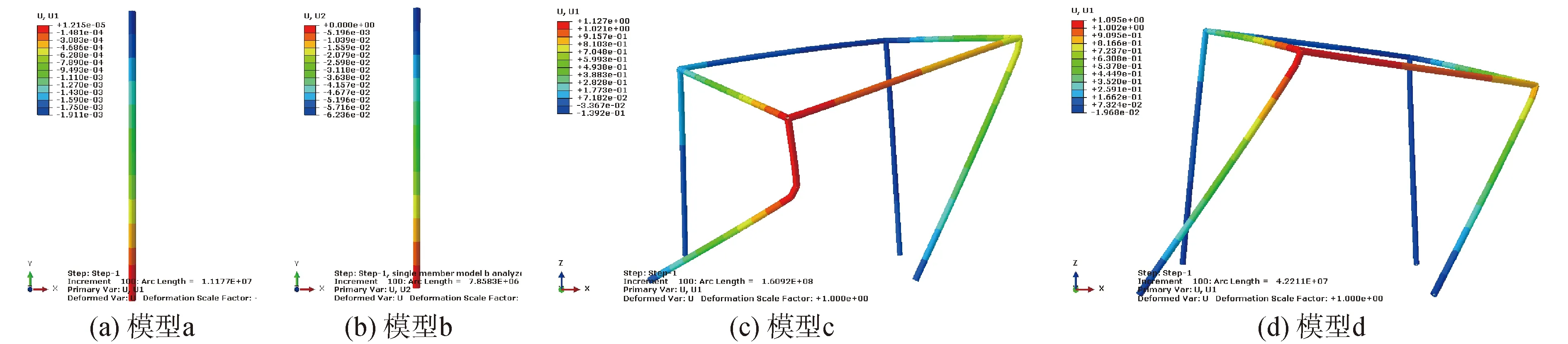
图5 桁架结构riks分析位移云图Fig.5 The displacement cloud map of simple truss analyzed by riks analysis
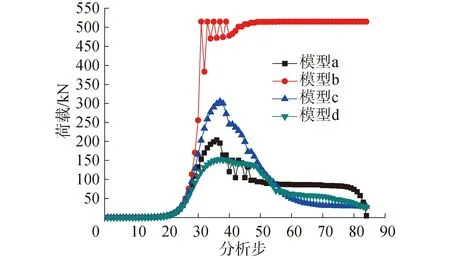
图6 桁架结构荷载加载曲线Fig.6 Load loading curves of truss structures
5 结论
1)桁架结构最不利杆件的确定充分考虑了结构布置形式、荷载分布、杆件与节点之间的连接以及材料非线性和几何非线性的影响。因此,基于桁架结构最不利杆件弹塑性屈曲承载力计算桁架结构屈曲承载力的计算方法是合理的、可行的。
2)根据本文所提方法计算的桁架结构弹塑性屈曲承载力与根据有限元模特征值屈曲分析方法和riks分析方法模拟的屈曲承载力结果较为接近,验证了本文所提方法计算桁架结构弹塑性屈曲承载力的正确性。
桁架结构的弹塑性屈曲承载力与结构的边界条件、荷载分布以及结构形式有关,进而对于复杂桁架结构的弹塑性屈曲承载力分析还有待更进一步的分析研究。
