自由变形在水翼外形优化设计中的应用
2020-11-19李靖璐王鹏牛宏磊张宁
李靖璐,王鹏,牛宏磊,张宁
(1.西北工业大学 航海学院,陕西 西安 710002; 2. 中国船舶重工集团 山西平阳重工机械有限责任公司,山西 侯马 043000)
水下滑翔机作为一种水下航行器,具有航行时间久、航行距离远、耗能低等特点,为监测海洋环境和勘探自然资源提供了方便,因而受到了广泛关注[1]。对于传统水下滑翔机,其双翼是升力的主要提供者,因此开展水翼外形优化设计研究对于提升传统水下滑翔机性能至关重要。外形优化设计首要的就是参数化方法。自由变形(free form deformation, FFD)参数化方法是一种最初用于计算机图形图像上的几何外形参数化方法[2],具有良好的光滑性和连续性,可以以较少的设计变量控制较为复杂的外形变形,在几何外形参数化上极具潜力。近年来,越来越多的学者在工程实际中选择使用这种参数化方法,机翼的气动外形优化设计[3-5]、车辆的外形设计[6]、舰船的船型外形设计[7]等。然而传统的FFD参数化存在着局部扰动能力差等缺陷。为了满足局部控制的需求,本文采用基于非均匀有理B样条(non-uniform rational b-splines,NURBS)的FFD参数法[8],改善了传统FFD方法局部扰动不足的缺点,光滑性及连续性更好,因而更适合于工程实践的外形参数化。此外,本文在FFD参数化方法的基础上,配合CFD求解及序列二次规划算法(sequential quadratic programming,SQP)搭建了一套外形优化设计框架。利用框架对NACA0012水翼进行了单点及多点外形优化设计,并对优化结果进行了分析与总结。
1 外形优化设计框架
本文搭建的外形优化设计框架是在已有工作基础上实现的[9],具体框架如图1所示。包括以NURBS为基函数的FFD参数化方法、CFD求解及优化3部分。

图1 外形优化设计框架Fig.1 Optimization framework
1.1 NURBS方法
NURBS方法是由B样条曲线方法通过加权、有理化发展而来[10],具体原理如下。
对于u方向为p阶、v方向为q阶的NURBS曲面表示为:
式中:Pi,j为控制网格上的控制点;wi,j为权值;Ni,p(u)和Nj,p(v)分别为节点矢量U和V上的无理B样条基函数;U、V的表达式为:
且有:
r=n+p+1,s=m+q+1
有理基函数的表达式为:
那么曲面方程可改为:
(1)
由式(1)可以看出,NURBS曲面是由u方向的(n+1)个控制点,v方向的(m+1)个控制点组成的(n+1)×(m+1)个控制点网格面,如图2所示。
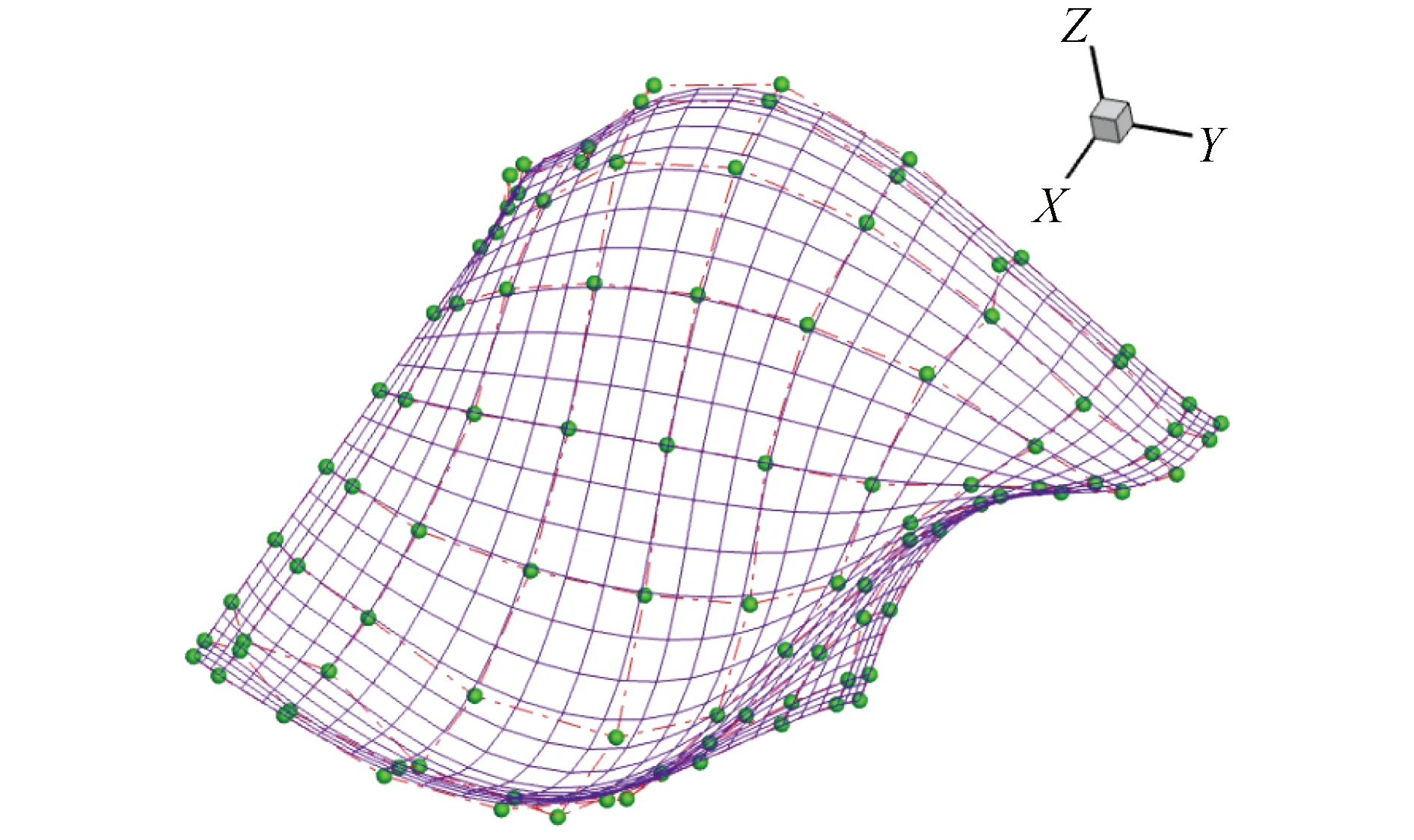
图2 NURBS曲面Fig.2 NURBS surface
1.2 FFD参数化方法
本文采用基于NURBS的FFD参数化方法[11-13],与FFD方法相比,其变形基函数由Bensteine基函数变为NURBS基函数,其基本原理如下:
首先在FFD控制体上添加一个局部坐标系O′-STU,则全局坐标系下任意点X,有:
X=X0+sS+tT+uU
式中X0为局部坐标系的原点在全局坐标系下的向量表示。局部坐标(s,t,u)写成向量形式为:
接下来在FFD控制体上建立网格点Pi,j,k,则初始模型与FFD控制体的映射关系为:
式中:wi,j,k为权因子;Ni,p(s)、Nj,q(t)、Nk,r(u)为以s、t、u为变量的p、q、r次基函数。
1.3 SQP优化算法
SQP是目前公认的求解非线性优化问题的最有效方法之一,可以很好地处理等式约束及不等式约束。其不仅具有全局收敛性,而且收敛速度快、计算效率高[14-15]。对于含不等式约束的优化问题:
在迭代过程中,首先将原问题转化为二次规划子问题:
(2)
式中:xk是第k次迭代的解;dk表示第k次迭代的搜索方向;Hk为Hessian矩阵的近似。
求解式(2),求得搜索方向dk,更新下次迭代解:
xk+1=xk+αkdk
(3)
式中αk可由线搜索方法得到。
修正Hessian矩阵近似Hk,重复上述迭代过程直至收敛。
2 外形优化仿真实例
利用外形优化设计框架对NACA0012水翼进行外形优化设计研究。其中数值模拟采用RANS方程作为控制方程,采用k-ω湍流模型,收敛条件为迭代2 000步或残差收敛小于1×10-6。
在外形优化之前,需要验证数值模拟的准确性。对NACA0012三维水翼进行CFD仿真,与文献[15]中的实验结果对比,结果如图3所示的流速为0.3 m/s下的升阻比曲线对比。结果表明在2°攻角下CFD仿真与实验结果之间误差最小。因此在采用2°攻角、0.3 m/s流速下的工况作为优化基础。
2.1 单点外形优化设计
优化设计目的为得到2°攻角、0.3 m/s流速的单个设计点下升阻比最大的水翼外形。其初始网格与FFD控制体如图4所示。

图3 升阻比曲线对比Fig.3 Comparisons of the lift-drag ratio
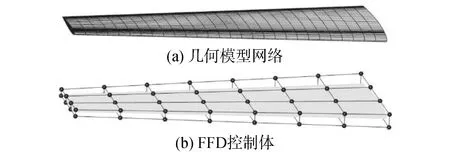
图4 几何模型网格与FFD控制体Fig.4 Baseline mesh and FFD volume
2.1.1 优化问题
优化目标函数为最大化NACA0012水翼的升阻比。设计变量为FFD控制点的位移,根据变形程度分为2类:1)单个控制点的位移,用于实现控制体的小变形,包括64个x向运动、64个y方运动、64个z向运动的设计变量(命名为x、y、z);2)一组控制点的移动,用于实现FFD控制体的厚度大变形(命名为thickness)。2种设计变量如图5所示。
约束条件分为2类:1)水翼的厚度约束,用于保证水翼的厚度不减;2)体积约束,用于保证水翼的体积不减。整个优化问题的数学表达如表1所示。

图5 设计变量Fig.5 Design variables

表1 优化问题表述Table 1 Optimization problem formulation
2.1.2 优化结果
优化收敛曲线如图6所示,共迭代14次,优化后升阻比为19.6。与初始18.1的升阻比相比,提升了8.46%。
比较优化前后的升力系数、阻力系数及升阻比,如表2所示。升力系数有所提升,阻力系数大大降低,整体升阻比获得了较大的提升,可以认为水翼得到了较好的外形优化结果。
在水翼沿弦长c方向上均匀的取3个截面,对比优化前后截面翼型如图7所示。可以发现变形主要集中在翼型上下表面及后缘位置。在满足厚度和体积约束的条件下,水翼厚度变薄的同时,后缘发生了一定的扭转,这是阻力系数降低,升力系数略微提升的主要原因。

图6 单点优化迭代收敛Fig.6 Iterative process of single-point optimization
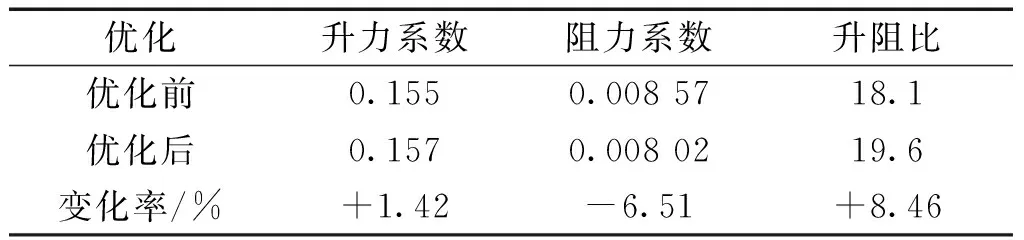
表2 单点优化水动力参数
2.2 多点外形优化设计
在2.1节中进行了水翼的单点优化,而在实际的工作环境中,很难保持水翼的速度为定值,往往伴随着一定的变化,为了模拟这样的实际工况,对NACA0012水翼进行了多点外形优化设计。多设计点为0.28、0.3、0.32 m/s。初始几何模型网格、FFD控制体与单点优化相同。
2.2.1 优化问题
优化目标函数为3个设计点下的平均升阻比。设计变量与约束条件与单点优化相同。最终优化结果要得到1个在3种工况下升阻比都能提升的水翼外形。
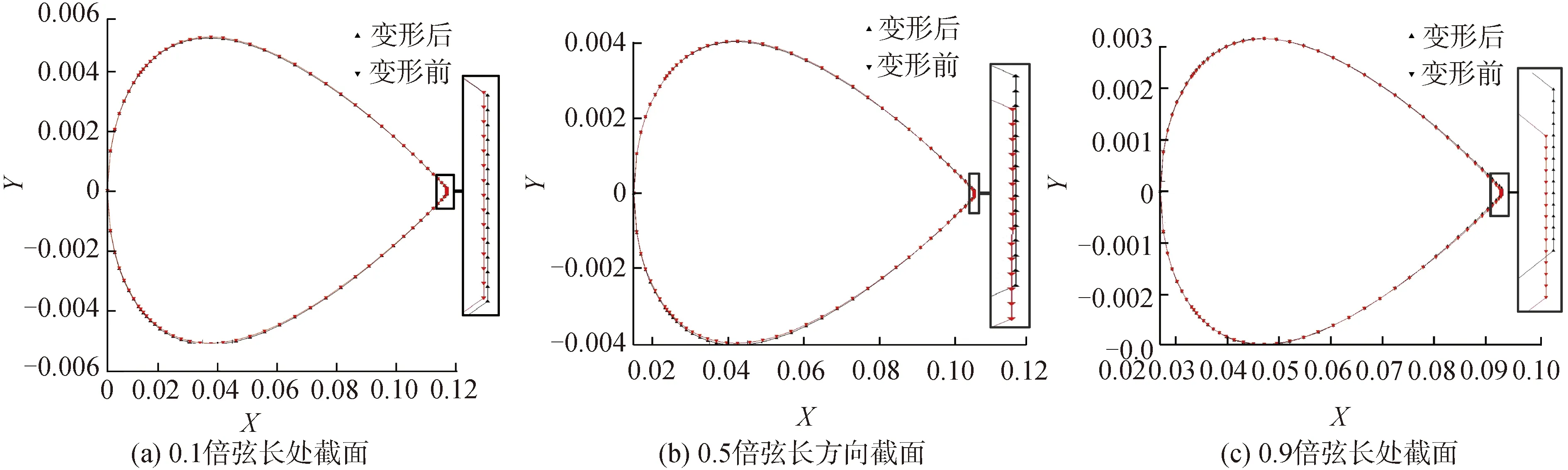
图7 单点优化水翼弦长方向截面对比Fig.7 Comparisons between the initial and the single-point optimized hydrofoil sections along chord length direction
2.2.2 优化结果
优化收敛曲线如图8所示,共迭代14次,最终平均升阻比为19.6,相比于初始平均升阻比18.1,提升了8.47%。
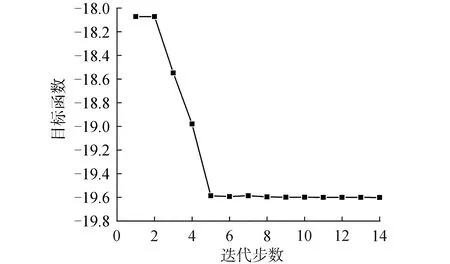
图8 多点优化迭代收敛Fig.8 Iterative process of multi-point optimization
比较3个工况优化前后的升力系数、阻力系数及升阻比,如表3所示。
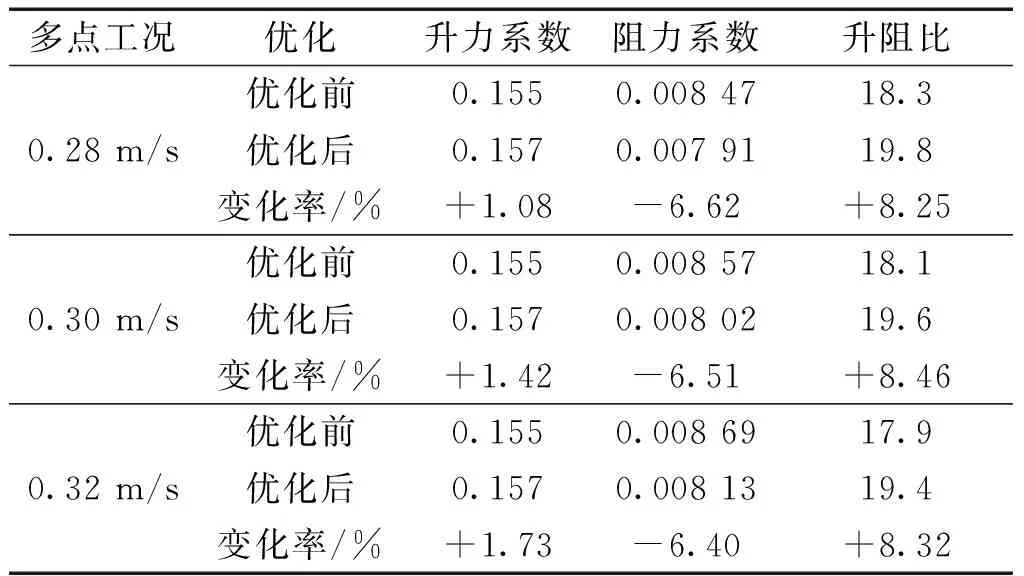
表3 多点优化水动力参数
3个工况下,升力系数均获得了提升,阻力系数均得到了降低。其中多点优化得到的外形在0.3 m/s工况下的提升程度与单点外形优化结果相同,在其他2种工况下也得到了较好的提升。综上所述,可以认为得到了较好的水翼外形。类似地,在同样位置处取3个截面,对比优化前后的翼型变化如图9所示。可以得到与单点优化相似的结论,即升阻比获得提升的原因是在满足约束的条件下水翼厚度变薄的同时,后缘发生了一定的扭转。
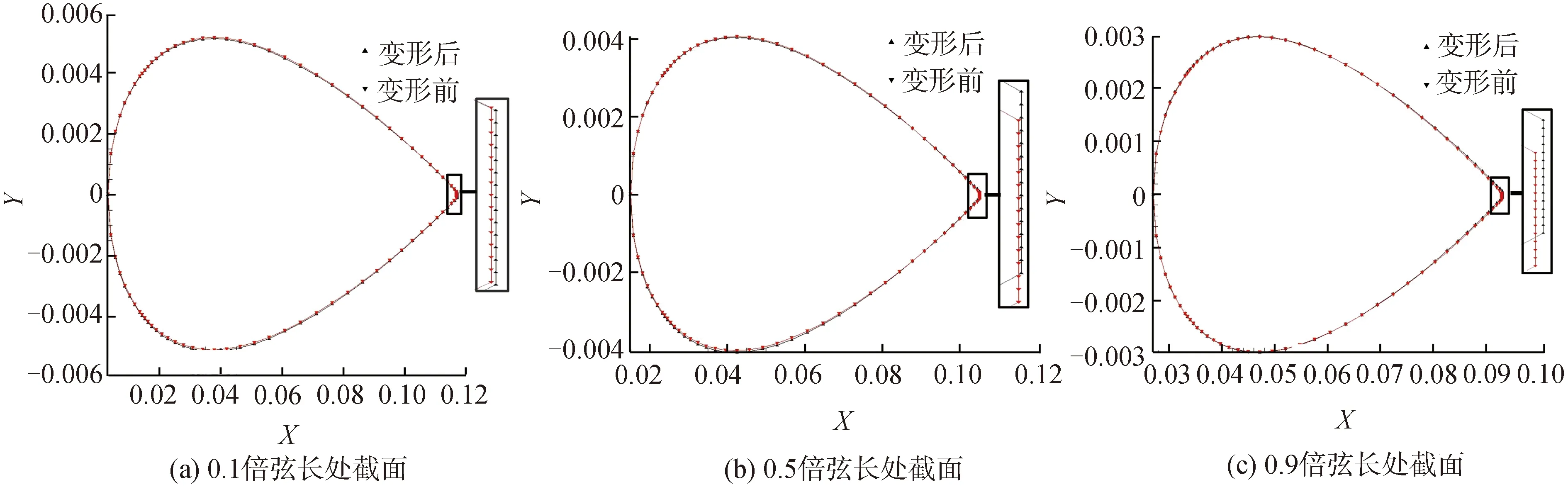
图9 多点优化水翼弦长方向截面对比Fig.9 Comparisons between the initial and the multi-point optimized hydrofoil sections along chord length direction
3 结论
1)单点优化设计在满足厚度、体积约束的条件下,升阻比提升了8.46%;
2)多点优化设计在在满足厚度、体积约束的条件下,平均升阻比提高了8.47%,此外3个工况下的升阻比均获得了较好提升;
3)水翼厚度减少降低了阻力系数,后缘扭转增大了升力系数;
本文在之前工作的基础上,实现了基于NURBS-FFD的外形优化设计框架,并成功用于水翼的外形优化设计。未来研究将在现有框架上进行网格变形、优化算法等功能拓展,以及实现结构优化、多学科优化等。
