远海无人快艇的自扶正优化设计方法

林焰，徐兴昂，叶超

(1.大连理工大学 船舶工程学院, 辽宁 大连 116024; 2.大连理工大学 工业装备结构分析国家重点实验室, 辽宁 大连 116024)

无人快艇作为智能化、机动化、无人化的海上交通工具，近年来在海洋勘探、海上救援、海洋环境监测等方面逐渐开始发挥巨大的作用[1-2]。随着人类在海上活动区域的不断拓展，无人快艇的作业海域也相应地逐渐向深、远海发展[3]。然而，相比于近岸处，远海的风浪流条件变得更加不利于浮体航行且难以预测[4]。同时，对于超出视距范围的自操控无人快艇而言，自发保持航行浮态是维持航线和有效避障的前提。因此，面对远海相对复杂及恶劣的海况，无人快艇应具备足够的稳性，甚至达到在任意角度下能够返回正浮状态的能力(简称为自扶正)。

国内外学者对无人快艇的自扶正性能开展了相关试验研究。 Grenestedt等[5]在超小型碳纤维高速艇“LORCA”中将甲板曲面设计为封闭形式，并通过试验证实了其具有自扶正性能，但其仍缺乏系统的自扶正设计方法；Akyldz等[6]利用具有水密功能的上层建筑为艇倒浮时提供充足的浮力以实现艇的自扶正，并通过与加装气囊或自操作式压载水置换系统作对比说明了前者实现自扶正的优势；景帅文等[7]提出利用自扶正气囊实现艇的自扶正，但采用设备进行自扶正，既浪费布置空间，增加载重量，频繁收放气囊也会使得无人艇的操纵问题变得更加复杂，不利于正常航行。

对于远海无人快艇而言，封闭甲板主要是作为提供稳性和保证艇体舱室水密性的构件，其功能相较于传统快艇甲板而言更为单一化。基于无人快艇的功能背景和远海的环境特点，本文引入了针对封闭式甲板的自扶正设计理念，以满足快速性、操纵性、基本稳性要求的快艇下艇体为基础，结合三维参数化技术的思想，通过引入若干个可变几何参数的甲板曲面控制点对封闭甲板曲面进行优化，实现了一种新型的无人快艇自扶正方案设计，并总结相应的设计方法。同时，依托于大连理工大学自主设计的无人快艇案例，应用该方法进行自扶正设计，提出优化后的设计方案。

1 无人快艇三维参数化设计

甲板曲面优化设计是一个复杂的过程，在整个周期中需要不断地优化与完善。为了提高设计效率，可以将一些重要的控制变量进行参数化处理[8-9]。在甲板系列化产品设计中，各方案和原型(或母型)产品之间的差别通常可以通过数学建模后几个关键的特征参量来体现，通过修改不同的参数可以得到性能不同的设计方案。基于以上参数化设计的思想，为了在设计螺旋线[10]循环的过程中筛选出满足自扶正要求且整体性能较优的甲板方案，本节对无人快艇完成自扶正功能的过程进行数学建模，并在下一章结合快艇稳性计算的物理模型进一步完成方案的设计和筛选[11]。

1.1 三维参数化建模

本文的总体设计思路是以型值不随自扶正优化而改变的快艇下艇体(如图1所示)为基础，对快艇的甲板曲面进行三维建模设计(如图2所示)，并以快艇自扶正性能为约束条件，逐渐优化甲板曲面的几何形状，最终获得符合约束条件且性能优良的快艇自扶正设计方案。

在进行甲板曲面优化设计时，通过修改甲板曲面的参数实现曲面的变换。为了保证甲板曲面变换过程中满足光顺性要求[12]，本文采用NURBS曲面片来表达甲板曲面[13]，并按照一定的约束条件对NURBS曲面片的控制顶点进行坐标变换，从而实现甲板曲面的几何变换。

图1 快艇下艇体Fig.1 Lower hull of the speedboat

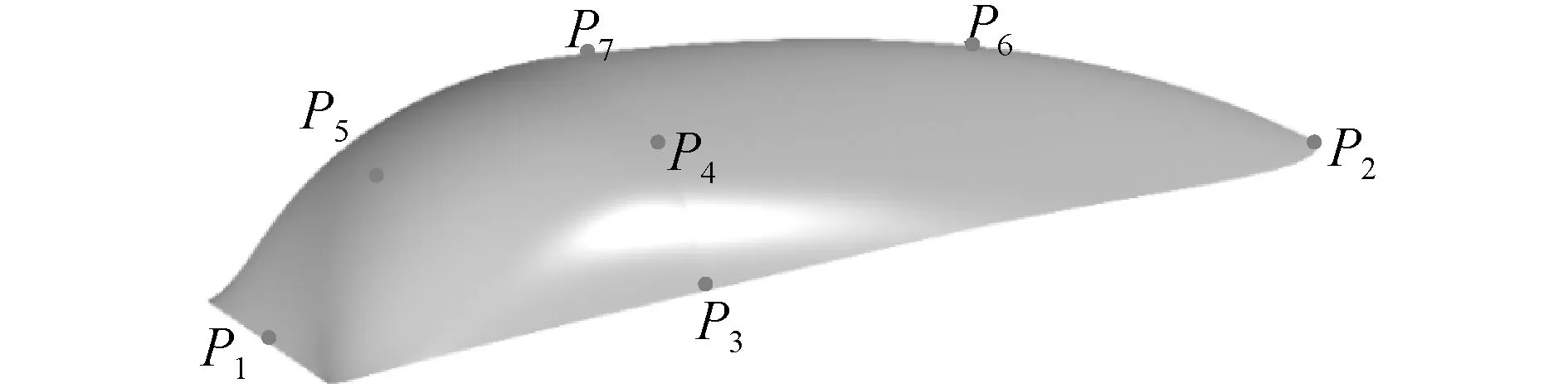
图2 甲板曲面控制点Fig.2 Deck surface control points

1.1.1 NURBS表达式

非均匀有理B样条(non-uniform rational b-splines, NURBS)曲面是目前应用最广泛的船体曲面表达方法之一[14]。船体曲面的NURBS表达式为:

(1)

式中：u、v为参数;m、n为U向与W向控制顶点的个数;Pi,j(0≤i≤m-1,0≤j≤n-1)为控制顶点，Pi,j由对应点的x、y、z3个坐标组成;Wi,j为权因子，Bi,q(u)和Bj,r(v)分别为沿U向的q次和沿W向的r次B样条基函数，分别由U方向上的节点矢量和W方向上的节点矢量控制，通常q和r均取3。本文基于改变式(1)中控制顶点Pi,j的坐标实现无人快艇自扶正的设计目标。

1.1.2 甲板曲面表达

在实际设计过程中，由于封闭甲板曲面存在部分接缝高阶不连续的可能性，虽然不影响其功能的实现，但利用整体表达法构建封闭甲板曲面难以对所有可行方案进行有效表达。因此，本文运用分片表达法[15]来构建封闭甲板曲面。图2中所示的点为本文构建封闭甲板曲面所取的控制点，通过改变这些点的坐标位置实现封闭甲板曲率[16]的变化。其中，点P1为艇艉顶点(中纵剖线与甲板边线的艉交点)，点P2为艇艏顶点(中纵剖线与甲板边线的艏交点)，点P3为甲板边线上不与P1、P2重合的某一点，点P3、P4、P7具有相同的纵向坐标，点P4、P5、P6具有相同的垂向坐标，点P1、P2、P5、P6、P7都在中纵剖线上。构建封闭甲板曲面的过程如下。

首先，创建图2所示的控制点，分别过P3、P4、P7，P1、P5、P7，P2、P6、P7生成如图3所示的NURBS曲线N1、N2、N3。其中，这3条曲线在P7处满足连续性原则。其次，以N1、N2和甲板边线为轮廓线，通过NURBS表达式计算曲面S1；同理，以N1、N3和甲板边线为轮廓线计算曲面S2。再次，以N1为交线拼接S1和S2，并使拼接处满足C2连续关系；利用相同方法构建无人快艇左舷的封闭甲板NURBS曲面。最后，以N2和N3为交线将快艇左右舷NURBS曲面进行拼接，并使拼接处满足C2连续关系。至此，封闭甲板曲面构建完毕。

图3 NURBS曲线曲面Fig.3 NURBS curve and surface

1.2 三维参数化设计方法

基于1.1节的三维参数化建模思路，无人快艇的参数化设计方法可以具体按以下步骤实施：

首先，在给定快艇下艇体的基础上构建一个平整的常规甲板曲面，提取出对构建甲板曲面起关键约束的控制参数，并分析这些控制参数之间的拓扑关系。其次，设计者根据参数之间的拓扑关系编写参数化程序，并将这些关键参数显示在人机交互窗口中，通过修改这些参数的可变范围和变化步距生成大量的甲板曲面设计方案。最后，根据约束条件筛选出最优的快艇自扶正设计方案。

2 无人快艇自扶正基本原理

2.1 快艇稳性评估

船舶在外力作用下偏离其平衡位置而倾斜，当外力消失后，能自行回复到原来平衡位置的能力，称为船舶稳性[17]。

图4(a)表示无人快艇的等轴侧视图，图4(b)～(e)分别表示无人快艇在不同横倾角度下的横剖面图。FG表示艇所受重力，B表示艇的浮心位置。当艇受到外力(倾斜力矩)作用时，其水线由正浮时的WL变化为WL1。这时艇的排水(水下)体积虽然数值大小没有改变，但其形状已经发生了一定的变化。此时，重力和浮力的作用线不在同一条铅垂线上，二者形成如图4(c)和(d)所示的力偶MR，该力偶使得艇能够回复到原来的平衡位置。

从重力作用点G作垂直于浮力作用线FB的垂线GZ，该垂线间长即为复原力臂l的代数值大小。力偶MR与复原力臂l存在下述关系：当l为正时，MR能够使艇回复到原来的正浮位置；当l为负时，MR不仅不能抵抗倾斜作用，而且使得艇继续倾斜；当l为零时，艇到达随遇平衡状态。可以看出，l的符号决定了艇倾斜状态下的自扶正能力。

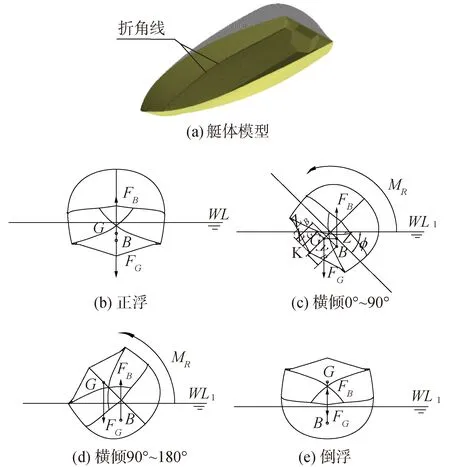
图4 无人快艇横剖面图Fig.4 Cross sectional view of unmanned speedboat

2.2 自扶正计算

由于本文研究的对象是远海无人快艇，因此致使快艇发生倾覆的因素主要来自于不确定性的风浪流。在快艇发生倾覆或自扶正的过程中，由于外在因素的影响，会使艇在回转运动过程中存在一定的角速度，因此若使艇在任意角度下都能够自动回复到正浮状态，即实现自扶正，只需保证复原力臂l在0°～180°始终大于零(允许l接近零的情况出现)。在下文中，满足自扶正条件的含义等同于复原力臂l在0°～180°始终大于零，并作为快艇自扶正设计的其中一个约束条件。另外，快艇具备自扶正能力后，0°～90°最大复原力臂lm是影响快艇稳定性的重要因素，lm愈大，快艇抗倾覆能力愈强，因此本文将lm作为快艇自扶正设计的优化目标。

如图4(c)所示，φ表示艇的横倾角度。艇坐标系下，浮心位置B假设已经确定，B的坐标值为(xB,yB,zB)，重心作用点G的坐标为(xG,yG,zG)。那么l的计算公式为:

l=yBcosφ+zBsinφ-zGsinφ

(2)

艇翻转过程中，其重心保持不变，而浮心的位置却是一个随φ改变的量。

本文采用等排水量计算法[18]并结合分段线性插值[19]编写相应的VB程序，确定不同横倾角φ时倾斜水线WL1的位置。此时，艇排水体积的形心即是浮心位置B。将B的坐标代入式(2)计算不同横倾角φ时的复原力臂l，进而判断其是否满足自扶正约束条件。

2.3 自扶正功能的整体实现流程

自扶正功能的整体实现流程如图5所示，其中k表示满足自扶正约束条件的设计方案数量，ε表示优化算法终止条件。通过图5，可以计算不同控制参数下的复原力臂，并获得符合约束条件的最优自扶正设计方案。

3 实例计算与分析

在该实例中，本文以大连理工大学自主研发的无人快艇方案为依托，以全封闭式无人快艇为例阐述自扶正的设计思想：即以“不改变已有艇体优化后的甲板边线以下型线”为前提，通过修改封闭甲板的设计参数来保证无人快艇的稳性和自扶正性能。其中，封闭甲板设计参数的改变基于本文提出的三维参数化设计思想加以进一步实现。

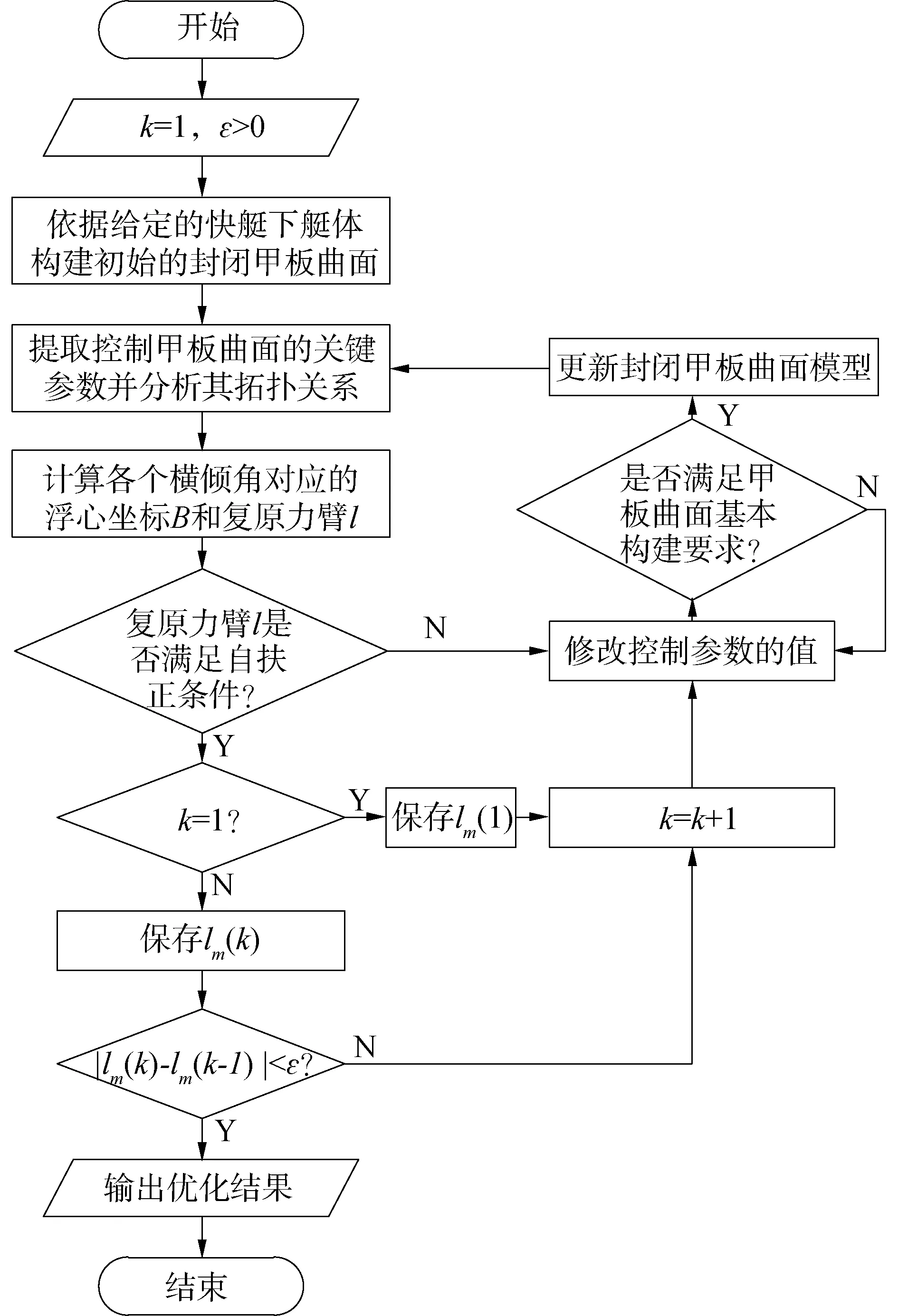
图5 自扶正功能实现流程Fig.5 Self-righting function implementation process

3.1 无人快艇方案

所述的无人快艇基本主尺度及性能参数如表1所示。

以上参数是通过前期对甲板边线以下型线优化设计后的最终结果，现基于以上条件进行甲板曲面的自扶正优化设计。在本文实例中，随着甲板曲面设计参数的改变，甲板曲面的表面形状和面积都会发生相应的变化。基于编写的自扶正计算VB程序，对参数改变后快艇的排水量Δ和重心G进行计算，并将计算结果代入式(2)计算不同甲板曲面对应的复原力臂。

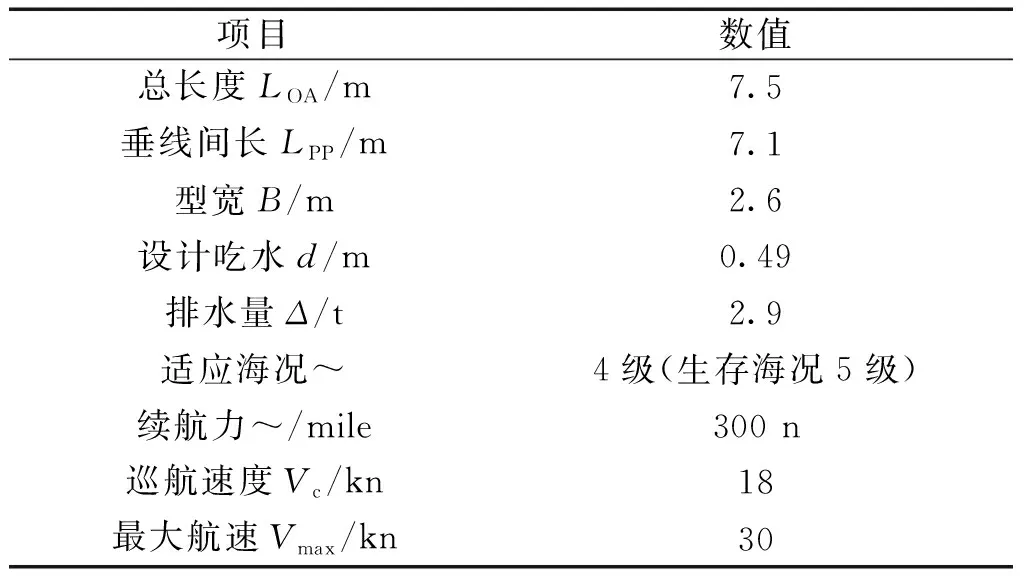
表1 无人快艇基本参数Table 1 Basic parameters of the unmanned speedboat

3.2 无人快艇的自扶正优化过程

3.2.1 数学模型的建立

以艇体基平面、中站面、中线面的交点为坐标原点O，艇体基线为x轴(艇首为正方向)，基平面与中站面的交线为y轴(右舷为正方向)，中线面与中站面的交线为z轴(向上为正方向)建立如图6所示的艇体坐标系Oxyz。其中，P1、P2的位置坐标在下艇体给定的前提下是确定的。设P1、P7之间的纵向距离为δx1，垂向距离为δz1，P2、P7之间的纵向距离为δx2。设P7的位置坐标为(x7, 0,z7)。根据已有的艇体坐标系，提取给定下艇体甲板边线对应的一系列坐标点，通过对坐标点线性插值得到甲板边线的空间方程h(x,y,z)=0。由于P3和P7的纵向坐标相等，则可以通过方程h=0求得P3的横向坐标y3，此时P3、P7之间的横向距离δy3=y3。设P5、P7之间的纵向距离δx5=μ1·δx1，垂向距离δz5=μ2·δz1，P6、P7之间的纵向距离δx6=μ3·δx2，P4、P7之间的横向距离δy4=μ4·δy3。其中μ1、μ2、μ3、μ4为比例系数。可以看出，通过修改P7的位置坐标和相应的比例系数可以改变控制点P3～P6的位置坐标，进而实现甲板曲面的变换。

图6 艇体坐标系Fig.6 Hull coordinate system

从稳性角度出发，本文将快艇自扶正设计优化问题简化为优化lm的单目标优化问题：将快艇0°～90°最大复原力臂lm作为优化目标，自扶正性能及甲板边线等作为约束条件，控制参数x7、z7、μ1、μ2、μ3、μ4作为变量建立无人快艇的自扶正数学模型：

(3)

3.2.2 自扶正方案的优化

以图6所示艇体坐标系为基准，该无人快艇实例中，甲板曲面控制点P1的位置坐标为(-3 540, 0, 953)，P2的位置坐标为(3 560, 0, 1 006)。给定控制参数x7、z7、μ1、μ2、μ3、μ4的初始值，通过前文叙述的步骤构建封闭甲板曲面，并计算对应的复原力臂l，若l满足自扶正条件，则可以得到当前控制参数下的lm。

针对优化目标lm的求解特点，本文使用粒子群算法[20]对快艇自扶正方案进行优化设计。粒子群算法相较于传统优化算法拥有更高的计算效率和全局搜索能力，且具有很好的收敛性能[21]。因此使用该算法有利于提高本文的自扶正优化设计效率。

在使用粒子群算法进行自扶正优化设计时，首先，根据控制参数取值范围对参数进行初始化，并计算每组迭代粒子的参数对应的lm。其次，按照算法的更新规则对参数进行更新，同时更新每组迭代粒子的最优值和全局最优值。最后，若算法满足终止条件，则结束算法并输出最终的优化结果lm，即maxlm，否则继续进行迭代计算。

3.3 最终设计方案

根据前文叙述的稳性基本原理和计算方法，以VB作为基本语言，编写无人快艇自扶正设计程序。其程序界面如图7所示。该程序具有以下功能：计算给定控制参数下的复原力臂；根据控制参数及约束条件，对快艇甲板曲面进行优化设计，得出最优的快艇自扶正设计方案，并输出优化结果。在运行该程序时，通过读取文件的形式将给定的快艇下艇体输入程序，并提取甲板边线作为设计约束。

首先，利用程序对前文所述的自主设计无人快艇进行复原力臂的计算。根据该无人快艇的设计要求，主机重心的纵向位置xM=-1 500 mm。如图8(a)、(b)所示，无人快艇的初始甲板为平甲板形式，此时，甲板曲面只受快艇下艇体约束，与控制参数无关。直接运行程序计算并绘制其对应的复原力臂曲线，结果如表2项目1和图9曲线1所示。可以看出，此时快艇的复原力臂不满足自扶正设计要求。为与自扶正设计后的计算结果作对比，设平甲板曲面对应的(x7,z7)为(-1 500, 1 050)，并取出自扶正设计程序在x7=-1 500 mm处的部分计算结果，得到如表2项目1～4和图9曲线1～4所示的对比结果。其中，比例系数(其值需要考虑快艇的设备布置)的取值如表3第2列所示。表2中ls表示最小复原力臂，φv表示稳性消失角。由表2和图9可以看出，当x7和比例系数一定时，随着z7的增大，快艇逐渐满足自扶正要求。另外，由于快艇的整体质量和重心高度随着z7的增大而增大，而快艇下艇体的型值在自扶正优化过程中保持不变，因此随着z7的增大，正浮状态到甲板边线入水角度范围内的复原力臂l逐渐减小。

图7 无人快艇自扶正设计程序界面Fig.7 Design program interface for self righting of unmanned speedboat

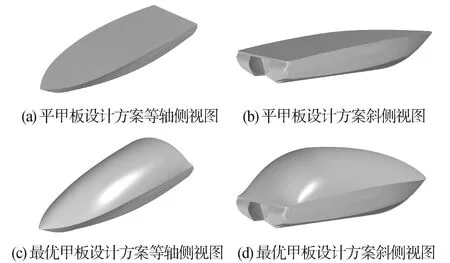
图8 无人快艇方案Fig.8 Unmanned speedboat scheme

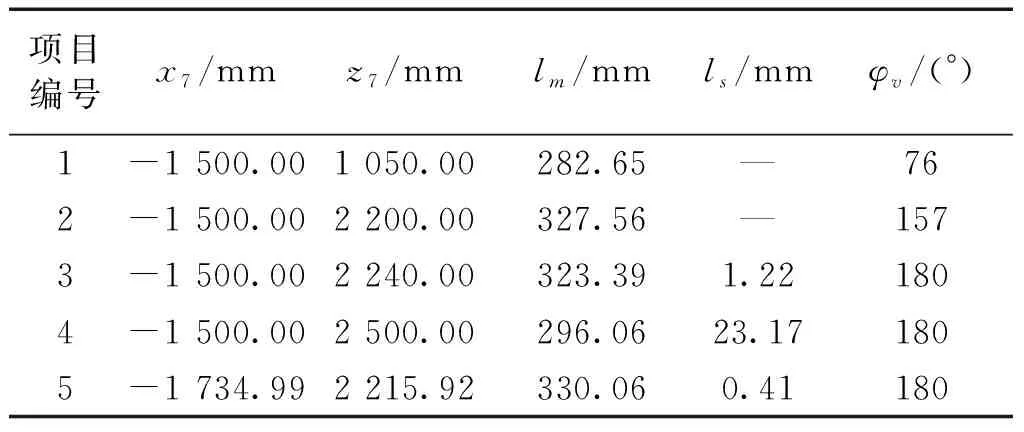
表2 自扶正设计计算结果Table 2 Calculation results of self-righting design

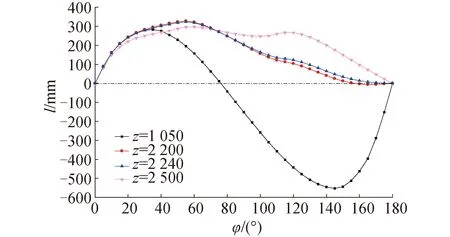
图9 复原力臂曲线Fig.9 Righting arm curves

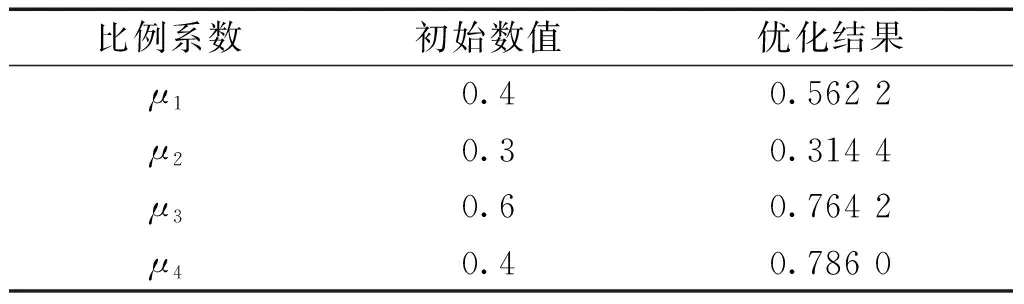
表3 甲板曲面比例系数Table 3 Proportional coefficient of deck surface

其次，利用程序进行快艇的自扶正优化设计。为保证程序的设计效率并考虑主机高度影响，同时结合给定下艇体的形状特征和前文中控制参数改变对复原力臂的影响分析，控制参数x7、z7、μ1、μ2、μ3、μ4的取值范围及粒子群算法的基本参数设置如图7所示。其中，N表示粒子种群规模，c1和c2表示加速常数，Tmax表示最大迭代次数，Pw表示惯性权重，其数值随迭代次数线性递减，PV1-PV6分别表示x7、z7、μ1、μ2、μ3、μ46个维度粒子的速度上限值。若算法连续迭代30次lm值不变即认为满足迭代终止条件。运行程序对控制参数进行初始化，并进行优化计算。可以得到如图8(c)～(d)所示的最优设计方案，其对应的最优控制参数及最优值如表2项目5和表3所示。同时，可以绘制出如图10所示的lm与迭代次数T关系曲线。

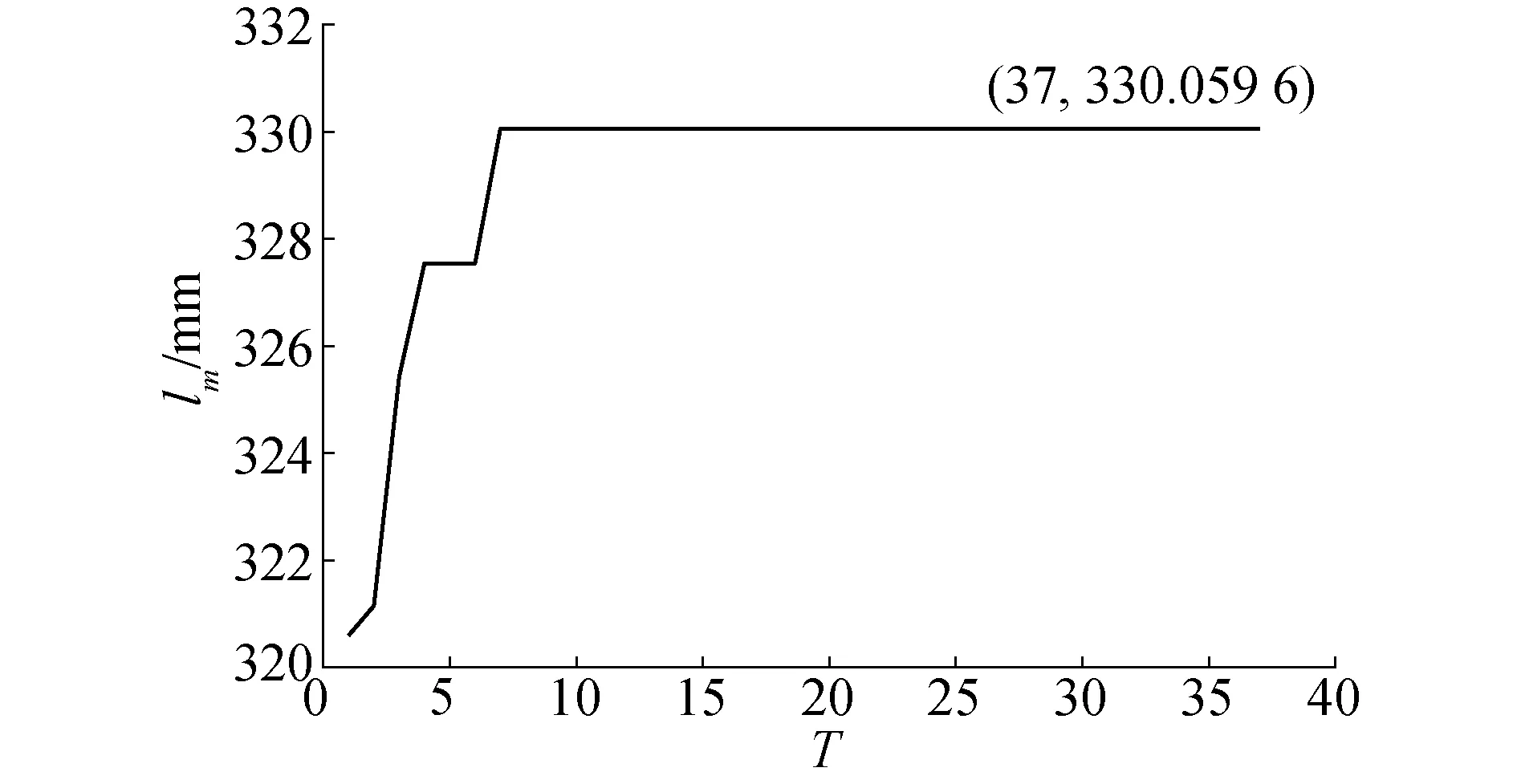
图10 lm曲线Fig.10 lm curve

4 结论

1)通过加装自扶正设备实现自扶正等传统方法在考虑快艇的快速性和空间利用方面存在着不足之处。相较而言，本文利用无人快艇甲板不需要布放驾驶室及除用于无人驾驶通讯导航之外的设备等优势，结合以往自扶正设计的研究，运用参数化设计思想对快艇甲板曲面进行几何变换，提出一种符合自扶正要求的无人快艇设计方法。

2)该方法运用有限个控制参数构建甲板曲面，由给定的快艇下艇体获取设计约束，并运用粒子群算法对优化问题进行求解，得到具有最大lm值且满足自扶正要求的远海无人快艇设计方案。

3)运用本文的方法在无人快艇的设计初期只需提供有限个约束条件内的控制参数便可以快速得到满足自扶正要求的优化设计方案；同时，运用该方法可以在不改变艇体快速性和操纵性的基础上，有效地实现自扶正功能；并且运用该方法进行无人快艇的自扶正设计，无需额外添加实现自扶正功能的设备，既节省了布置空间，又节约了增添自扶正设备的成本，且有效地拓展了水密甲板的功能。

在计算复原力臂l时，本文只考虑了横倾的情况。但是对于高速小艇而言，在横倾的同时会产生一定程度的纵倾。因此，在接下来的研究中，本课题将进一步考虑纵倾的影响，从而使计算结果更符合实际情况。