基于EKF的轨道探伤小车组合定位技术研究

2020-11-19刘长军王黛月余天乐郭建志李锦

铁道科学与工程学报 2020年10期

刘长军，王黛月，余天乐，郭建志，李锦

刘长军1，王黛月1，余天乐2，郭建志2，李锦1

(1.华东理工大学机械与动力工程学院，上海 200237；2. 上海市东方海事工程技术有限公司，上海 200011)

轨道探伤小车是新一代铁路轨道探伤设备，现已具备伤损点自动识别功能，但其定位依赖单一里程计，仍需人工标定来完成伤损点的实时地理位置定位，无法满足伤损定位的精度要求和实现全面自动伤损扫查检测功能的需求。针对铁路线上伤损扫查过程中的自动定位问题，使用扩展卡尔曼滤波(EKF)实现了里程计与全球卫星导航系统(GNSS)的多传感器数据融合，并基于新息自适应估计(IAE)对融合算法作自适应处理，建立GNSS/里程计组合定位模型，以提高探伤小车定位的精确性与可靠性。最后设计开发了硬件板卡，并通过沪杭线上测试实验，对组合定位模型进行验证。实验表明基于EKF的组合定位相较于单一GNSS定位其定位精度和鲁棒性明显提高。

轨道探伤；扩展卡尔曼滤波；数据融合；自适应；组合定位

随着我国铁路交通进入高速时代，运营里程与载客量在不断上升，为保证铁路安全，钢轨探伤密度也随之增加，这对原有的探伤设备提出了新的要求。长期以来，我国用于钢轨探伤的设备主要有2种，分别是手推式探伤仪与大型钢轨探伤车，前者工作效率低且工作强度高，后者效率高但其价格过于昂贵无法大量使用[1]。轨道探伤小车是新一代铁路轨道探伤设备，相较于前两者，具有轻量化、模块化、合理化等特点，目前探伤小车已能自动识别出钢轨损伤点，但其对伤损点的定位主要依靠车载里程计，里程计定位属于相对定位，短期内定位精度高但不可避免的存在累积误差，需要人为地根据地理路标进行航迹推算与误差校正。而为了推进轨道探伤车工作效率的进一步提升，实现损伤全面自动化检测功能，这就需要探伤小车具备全自动的精确定位功能。全球卫星导航系统(GNSS)是各种卫星定位系统的统称，其定位范围广、精度高，能够获得车辆的实时坐标信息，可以有效解决探伤小车自动定位的问题，但是GNSS定位原理是基于卫星发送的电磁波信号，当小车行驶路段存在过多遮挡与干扰时，就会导致定位偏差过大或信号丢失等问题[2]。由此可见，单一传统的定位传感器满足不了探伤小车所需高精度、高可靠性的定位要求。而多传感器信息融合技术可以有效解决这一问题，将探伤小车的里程定位与GNSS定位相结合，互相取长补短，所构成的组合定位系统，具有更高的精度与鲁棒性。目前，能够实现数据融合方法有很多，主要包括加权平均法、贝叶斯估计法、卡尔曼滤波法、产生式规则、人工神经网络、模糊推理等[3]。其中，卡尔曼滤波法是多传感器信息融合技术在定位研究应用中比较常用的方法，其设计原理源于最小线性方程估计[4]，是线性动态系统中的最优化估计。但实际上在现实中大多数问题都是由非线性和时变系统所组成，使用线性卡尔曼滤波难以进行分析估计[5]。而人们在处理一些非线性系统的问题中仍期望使用卡尔曼线性滤波估计的形式，进而发展出了扩展卡尔曼滤波(EKF)，具有更强的广泛适应性和稳定性[6]。然而，与标准卡尔曼滤波器一样，EKF在使用前需要已知目标系统的噪声统计特性，但对于更多系统的来说其外部环境是未知且多变的，这就容易引起滤波发散，从而容易引起滤波发散[7]。为了防止滤波发散，需要先判断出系统当前状况，然后使用不同方法通过自适应的方式来抑制发散，新息可以用作判断和调节滤波器的依据[8]。卡尔曼滤波器的自适应处理方法主要有两种，一是基于多模型自适应估计(MMAE)建立多模型卡尔曼滤波器[9]，二是基于新息自适应估计(IAE)来修正过程参数[10]。而后者还与模糊控制相结合，进一步形成了基于模糊控制的卡尔曼滤波自适应技术[11]。除此之外，国内外的自适应方法还存在有Saga-Husa滤波法[12]，抗差滤波法[13]，渐消记忆因子滤波法[14]等。针对GNSS定位存在的信号不稳定以及里程计定位的累积误差等问题，使用EKF来实现GNSS与里程计数据融合的定位方法，通过该融合算法对定位坐标进行实时的校准与更新，并基于IAE对融合算法中的误差参量作自适应处理，建立了组合定位模型，提高了在GNSS观测量发生突变时该卡尔曼滤波器的精度和鲁棒性。本文针对GNSS定位存在的不稳定以及里程计定位的累积误差等问题，使用扩展卡尔曼滤波(EKF)来实现GNSS与里程计融合的定位方法，通过该融合算法对定位坐标进行实时的校准与更新，从而实现对GNSS失信状态与里程计累积误差的周期性补偿和校正，并基于IAE对融合算法中的误差参量作自适应处理，建立组合定位模型，提高了在GNSS观测量发生突变时该卡尔曼滤波器的精度和鲁棒性。并设计开发基于树莓派3b的硬件板卡，实现探伤小车精确定位的自动输出，最终在上海市松江区沪杭线上进行测试，对本文所提出的方法和理论进行验证。

1 基于EKF的自适应算法

1.1 EKF算法

在面对非线性问题时，EKF的基本方法是对其估计模型进行一阶泰勒展开，在短区间内将非线性模型线性化，然后再进行滤波估计[15]。

对于非线性系统模型，其状态方程与测量方程如下：

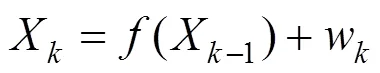
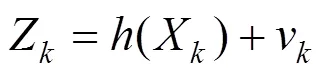
式中：为当前时刻；为系统状态描述矩阵；为由上一时刻到下一时刻的状态转移方程；为测量转移方程；w与v分别代表系统过程噪声与测量噪声，两者互不相关，他们的协方差矩阵分别为跟。有了系统状态变化过程的公式，扩展卡尔曼滤波算法具体流程如下：

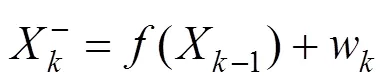
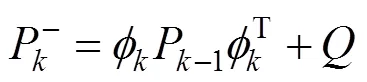
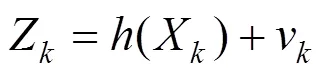
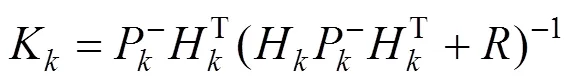
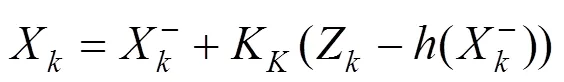
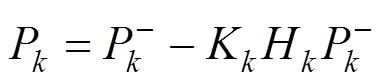
假设系统存在一个维的状态变量:

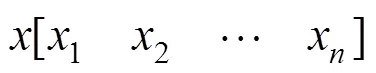
则其转置矩阵为：

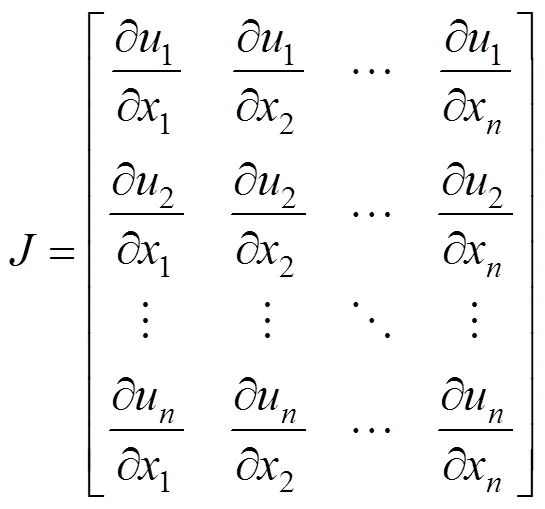
EKF基于微分思想将非线性问题化为多段线性问题并加以解决处理，极大的提升了卡尔曼滤波的适用性与其解决实际问题的能力。

1.2 自适应算法

虽然EKF可以解决非线性问题，然而基本过程还是基于标准卡尔曼滤波，其滤波方程中的与需要提前确定，常用的方法是利用相关噪声在系统环境中的统计特性来代替。但在实际过程中，系统环境可能是复杂且多变的，这就很难保证统计特性的准确性。因此，将滤波方程中的噪声协方差矩阵跟不再设为预先统计而得的固定值，而是作为变量随系统时间与环境的变化而变化，达到其自适应性的目的。对于噪声更迭的自适应方式有很多，其中最常见的是利用系统新息来自适应的迭代更新噪声[16]。

新息的定义为：

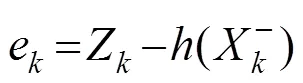
新息的方差为：

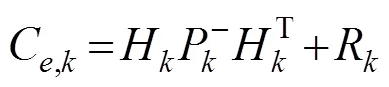
取时刻前个观测新息可计算出观测新息协方差的估计值：

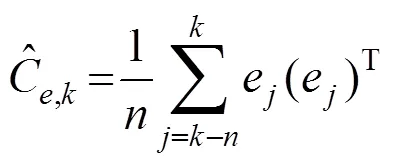
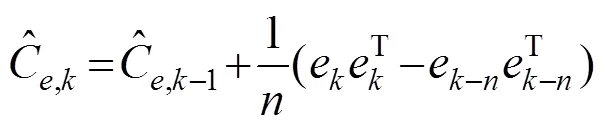
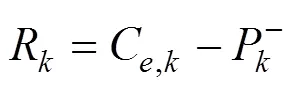
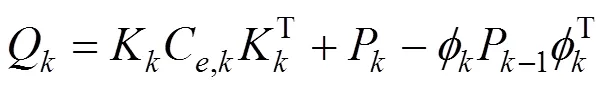
1.3 融合算法推导

将上述1.2中的式(11)、式(14)～(16)代入到1.1中式(3)～(8)的EKF算法的流程中去，即可得到经自适应处理后的EKF算法，最终融合算法如下：

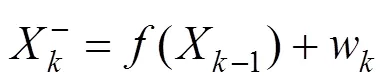
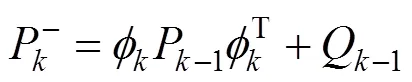
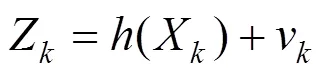
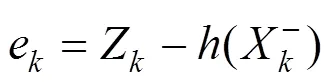
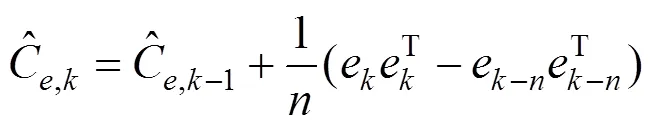
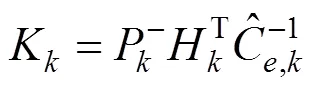
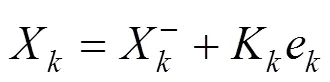
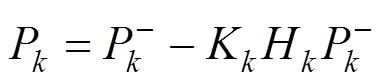
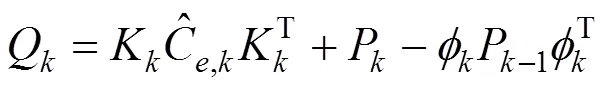
2 GNSS/里程计组合定位系统模型

2.1 坐标转换

利用GNSS进行定位时，探伤小车上的接收机能直接获得的是WGS-84下的经纬度数据，而使用里程计作航迹推算时一般是采用高斯平面直角坐标系。因此，不能直接将两者定位信息进行融合处理，需要统一坐标系。本文使用高斯−克吕格投影法将接收机获取的经纬度坐标转至平面坐标。

把接收机获取的经纬度坐标(,,)按如下公式转换成平面坐标：

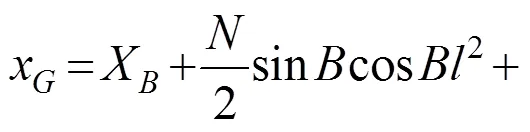
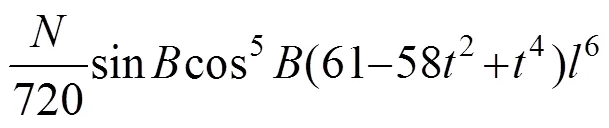
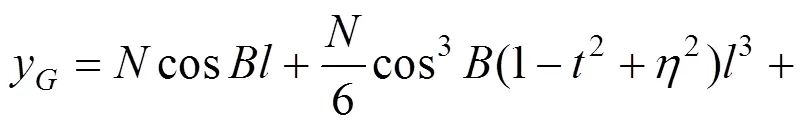
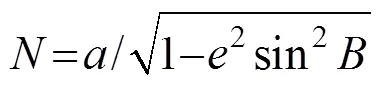
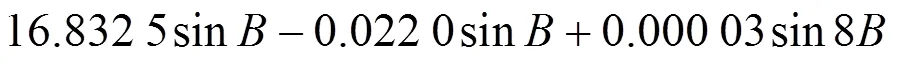
2.2 组合定位系统预测模型

设探伤小车的位姿向量为:

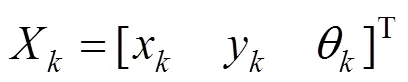
位姿向量的预测方程为：

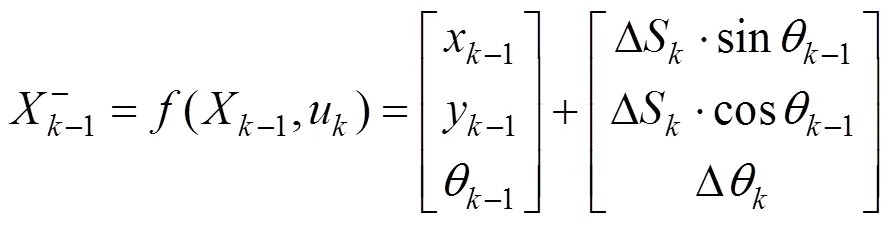
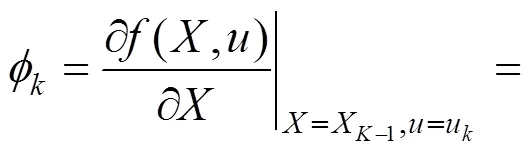
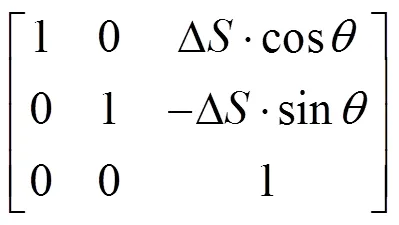
由此，与系统预测过程所对应的估计误差协方差矩阵更新方程为：

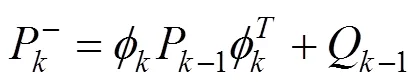
2.3 组合定位系统测量模型

设在时刻，经GNSS直接测量转换所得的观测量Z与位姿向量的关系为：

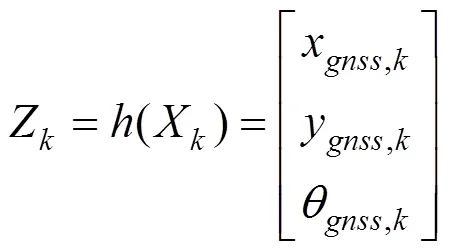
观测方程关于探伤小车位姿向量经雅比克变换后的转置矩阵为：

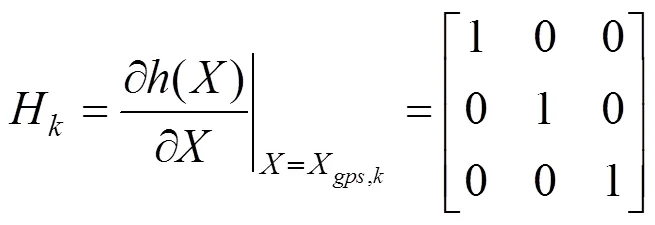
至此，将系统模型与观测模型代入基于EKF的自适应算法中进行测试分析。

3 探伤小车松江线上测试结果与分析

为验证融合定位算法的效果，设计开发了组合定位系统，图1为该系统的总体框架图，主要包括工控机(即探伤小车控制系统)、中央处理模块、定位模块、通讯模块以及远程监控平台，其中工控机采用的是上海东方海事工程技术有限公司研发的双轨式钢轨超声波探伤仪，中央处理模块为搭载Raspbian系统的树莓派3b板卡，GNSS模块为QUELTEL公司旗下的GNSS L76，通讯模块为华为ME909S-821，远程监控平台为基于C#在QT平台下开发的界面操作软件，软件中搭载有自适应融合算法，能分别输出单一GNSS定位数据与组合定位数据。

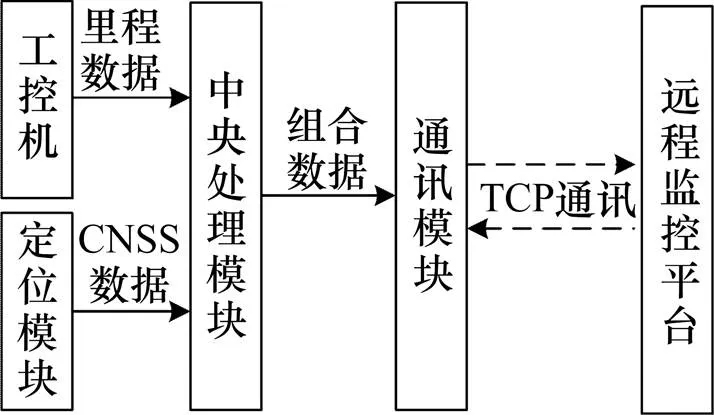
图1 组合定位系统

本文采用一组位于上海市松江区沪杭线铁路工段进行的试验数据对本文提出的自适应融合算法进行测试，测试路段全长约为6.4 km。组合定位系统的里程精度与定位测量精度分别为：里程1.5%，定位小于2.5 m CEP，但同时在实际测试过程中发现，GNSS易受户外环境因素干扰，定位精度不稳定。行驶平均速度为8 m/s，探伤小车行驶时间为800 s。选取其中匀速行驶的两段数据，其中段一存在GNSS无信号区域，全长约300 m，包含无信号区200m。段二全程GNSS信号良好，全长约800 m，其GNSS数据点=200，采样周期为= 0.5 s。利用GNSS获得的探伤小车位姿作为观测量引入卡尔曼滤波器，得到误差的最优估计。图2为段一即存在信号丢失段的定位轨迹比较图，图3为段二即信号良好段所选取的GNSS定位轨迹点。

首先对段一测试效果进行评价，如图2所示，当探伤小车途径无信号区段时，单一GNSS将失去定位功能，定位轨迹中出现缺失段；而组合定位依靠里程计的航迹推算仍能持续定位，相较于单一GNSS定位，更能有效的保障探伤小车连续定位，提高了定位系统的鲁棒性。

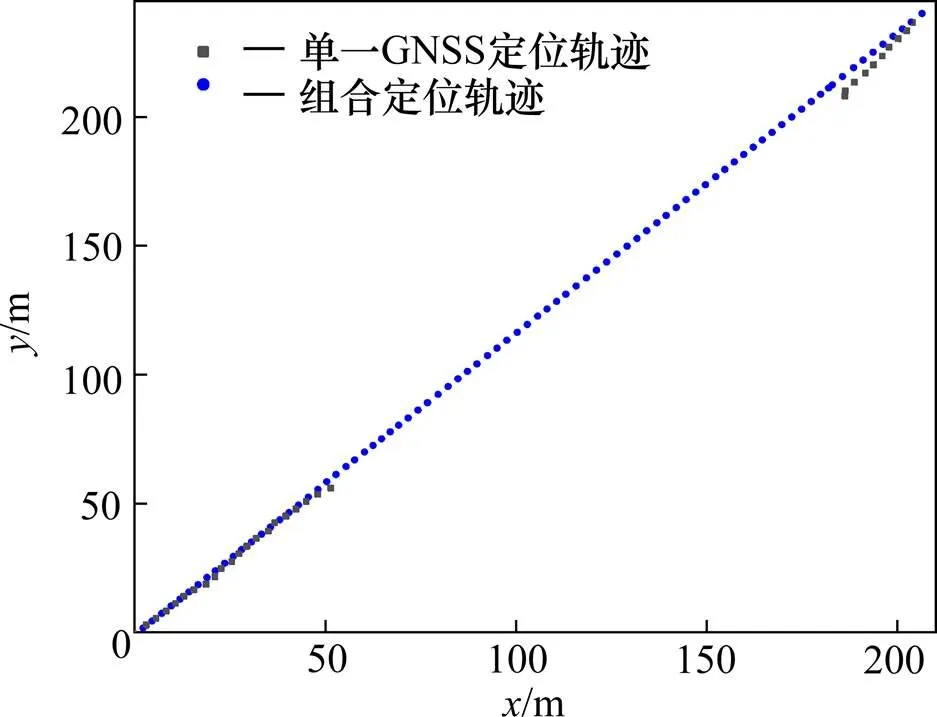
图2 信号丢失段定位轨迹

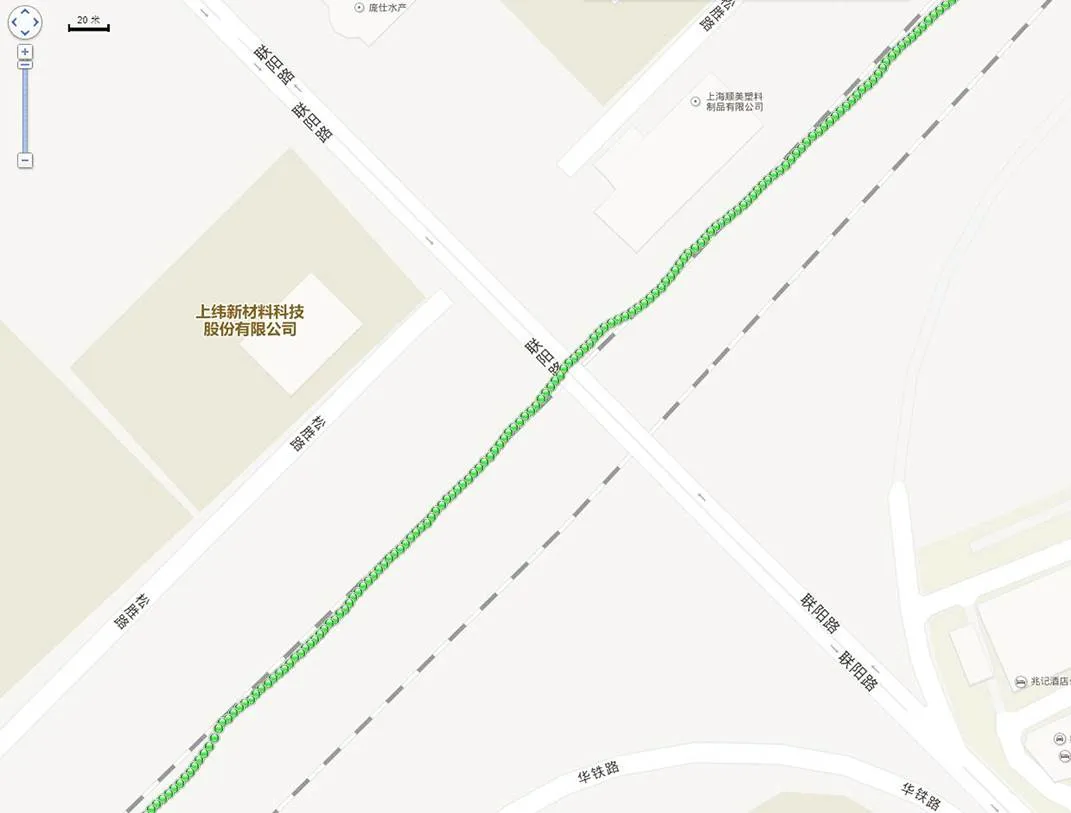
图3 地图上探伤小车GNSS定位点

在段二中，本测试首先在图示地图上对该铁路段真实坐标进行图上采点，再经坐标转换后进行拟合，得到该路段探伤小车行驶的真实轨迹，然后以真实轨迹作为基准，分别计算出单一GNSS定位与组合定位的偏离程度，并进行对比分析。图4为GNSS定位与组合定位相较于真实轨迹的偏离误差比较。

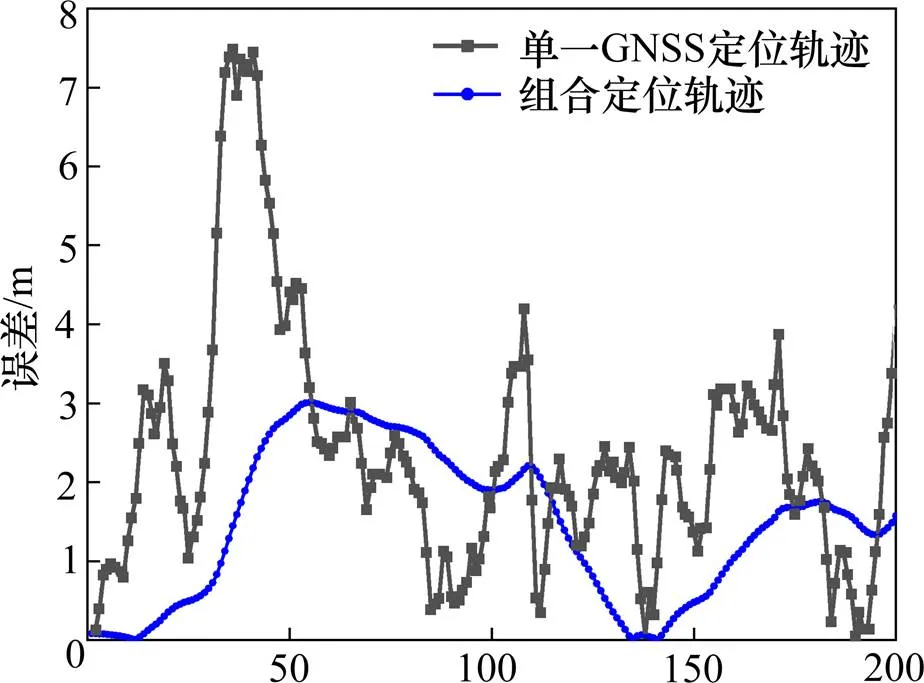
图4 单独GNSS定位与组合定位的误差对比

由图4可以看出，相较于单一GNSS定位，组合定位在GNSS测量发生较大变化时可以有效减小定位误差，从GNSS定位误差最大的7.479 m减小到组合定位误差的3.010 m，以及从GNSS定位误差均值的2.396 m减小到1.498 m。单一GNSS定位与组合定位误差比较如表1所示。

表1 定位误差统计

3 结论

1) 针对目前轨道探伤小车对于全自动精准定位功能的需求，基于多传感器信息融合技术将小车的里程计与卫星定位系统相结合，构建多传感器组合定位系统，实现了两者的优势互补，保证了小车自动定位的连续性和可靠性。

2) 采用EKF对小车组合定位系统的融合算法进行设计，并基于IAE对融合算法中的误差参量作自适应处理，建立基于GNSS/里程计的组合定位模型，能有效的提高定位精度与系统的鲁棒性。

3) 设计开发组合定位软硬件系统并使用该系统对融合算法进行数值模拟和实验验证。结果表明使用该组合定位系统能弥补单一GNSS定位精度不足的问题，减小定位误差并提升稳定性，即使在GNSS信号受到遮挡时，也可以利用里程计航位推算的定位方式进行辅助定位。该算法为铁路自动探伤提供了可靠的定位方法，为实现全面自动探伤扫测定位提供了可靠的现场应用方案。

[1] 韩小平. 基于高速探伤技术的双轨自行式钢轨探伤小车研制[J]. 中国铁路, 2014(3): 77−81. HAN Xiaoping. Development of double rail self- propelled rail inspection car based on high speed inspection technology[J]. China Railway, 2014(3): 77−81.

[2] 蔡煊, 王长林. 基于抗差估计的BDS/ODO组合列车定位方法[J].铁道科学与工程学报, 2018, 15(10): 2654−2660. CAI Xuan, WANG Changling. BDS/ODO integrated train positioning method based on robust estimation[J]. Journal of Railway Science and Engineering, 2018, 15(10): 2654−2660.

[3] 胡胜豪. 室外移动机器人的定位与运动控制研究[D]. 哈尔滨: 哈尔滨工业大学, 2016: 5−6. HU Shenghao. Research on localization and motion control for outdoor mobile robot[D]. Harbin: Harbin Institute of Technology, 2016: 5−6.

[4] ZHAO Yingwei. Performance evaluation of Cubature Kalman filter in a GPS/IMU tightly-coupled navigation system[J]. Signal Processing, 2016, 119: 67−79.

[5] WANG Shiyuan, WANG Wanli, CHEN Badong, et al. Convergence analysis of nonlinear Kalman filters with novel innovation-based method[J]. Neurocomputing, 2018, 289: 188−194.

[6] 刘梦佳, 孙自强, 卿湘运. 一种基于简化MRAS无速度传感器的永磁电机EKF磁链辨识[J]. 华东理工大学学报(自然科学版), 2015, 41(2): 222−230. LIU Mengjia, SUN Ziqiang, Qing Xiangyun. Flux identification of SPMSM based on simplified MRAS senseless control system[J]. Journal of East China University of Science and Technology (Natural Science Edition), 2015, 41(2): 222−230.

[7] 李旦, 秦永元, 梅春波. 组合导航自适应卡尔曼滤波改进算法研究[J]. 测控技术, 2011, 30(3): 114−116. LI Dan, QIN Yongyuan, MEI Chunbo. An improved adaptive Kalman filter algorithm for SINS/GPS integrated navigation system[J]. Measurement & Control Technology, 2011, 30(3): 114−116.

[8] 卞鸿巍, 李安, 覃方君, 等. 现代信息融合技术在组合导航中的应用[M]. 北京: 国防工业出版社, 2010: 115−117. BIAN Hongwei, LI An, QIN Fangjun, et al. Application of modern information fusion technology in integrated navigation[M]. Beijing: National Defense Industry Press, 2010: 115−117.

[9] Alsuwaidan B N, Crassidis J L, CHENG Y. Generalized multiple-model adaptive estimation using an autocorrelation approach[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(3): 2138− 2152.

[10] DING Weidong, WANG Jinling, RIZOS C. Improving adaptive Kalman estimation in GPS/INS integration[J]. Journal of Navigation, 2007, 60(3): 517−529.

[11] JIN Mei, ZHAO Jinge, JIN Ju, et al. The adaptive Kalman filter based on fuzzy logic for inertial motion capture system[J]. Measurement, 2014, 49: 196−204.

[12] WANG Qinghui, HUANG Wangyuan, WEI Lifeng, et al. A wireless localization algorithm based on strong tracking Kalman filter[J]. Sensors & Transducers, 2014, 183(12): 155−161.

[13] Chingiz H, Halil E S. Robust adaptive unscented Kalman filter for attitude estimation of pico satellites[J]. International Journal of Adaptive Control and Signal Processing, 2014, 28(2): 107−120.

[14] Hajiyev C, Soken H E. Adaptive Kalman filter with multiple fading factors for UAV state estimation[J]. IFAC Proceedings Volumes, 2009, 42(8): 77−82.

[15] 谷丰, 周楹君, 何玉庆, 等. 非线性卡尔曼滤波方法的实验比较[J]. 控制与决策, 2014, 29(8): 1387−1393. GU Feng, ZHOU Yingjun, HE Yuqing, et al. Experimental investigation and comparison of nonlinear Kalman filters[J]. Control and Decision, 2014, 29(8): 1387−1393.

[16] 符拯, 王书满, 刘丙杰. 自适应卡尔曼滤波的最新进展[J]. 战术导弹技术, 2009(6): 62−66. FU Zheng, WANG Shuman, LIU Bingjie. An overview of the development of adaptive Kalman filtering[J]. Tactical Missile Technology, 2009(6): 62−66.

[17] 马瑞平, 魏东, 张明廉. 一种改进的自适应卡尔曼滤波及在组合导航中的应用[J]. 中国惯性技术学报, 2006, 14(6): 37−40. MA Ruiping, WEI Dong, ZHANG Minglian. Improved adaptive Kalman filter for GPS/INS integrated system [J]. Journal of Chinese Inertial Technology, 2006, 14(6): 37−40.

[18] 卞鸿巍, 金志华, 王俊璞, 等. 组合导航系统新息自适应卡尔曼滤波算法[J]. 上海交通大学学报, 2006, 40(6): 1000−1004. BIAN Hongwei, JIN Zhihua, WANG Junpu, et al. The innovation based estimation adaptive Kalman filter algorithm for INS/GPS integrated navigation system[J]. Journal of Shanghai Jiaotong University, 2006, 40(6): 1000−1004.

[19] 吴显. 基于多传感器信息融合的移动机器人定位方法研究[D]. 北京: 北京交通大学, 2016: 17−19. WU Xian. Research on localization method of mobile robots based on multi-sensor data fusion[D]. Beijing: Beijing Jiaotong University, 2016: 17−19.

Research on combined location method of dual rail inspection vehicle based on extended Kalman filter

LIU Changjun1, WANG Daiyue1, YU Tianle2, GUO Jianzhi2, LI Jing1

(1. School of Mechanical and Power Engineering, East China University of Science and Technology, Shanghai 200237, China;2. Shanghai Oriental Maritime Affairs Engineering Technology Co., Ltd., Shanghai 200011, China)

Dual rail inspection vehicle is a new generation of railway inspection equipment, which has the function of automatic inspection of rail defect points. Conventionally, the localization of the inspection vehicle uses an odometer and the real-time localization of rail defect points still needs manual calibration. Thus, it cannot achieve the localization accuracy as well as the requirements of vehicle automatic operation. The automatic localization methods were discussed in this paper. The Extended Kalman Filter (EKF) was employed for the multi-sensor data fusion of the odometer and the Global Navigation Satellite System (GNSS). Then the fusion algorithm was processed using the Innovation Adaptive Estimation(IAE). The GNSS/odometer combined localization model has been built to improve the accuracy and reliability of the inspection vehicle localization. The hardware board was designed. Finally the on-line test has been performed on the Shanghai-Hangzhou railway line. The experimental results show that our combined localization method can significantly improve the accuracy and robustness compared with that of the single GNSS method.

rail inspection; extended Kalman filter; data fusion; adaptive; combined localization