黄金比例NSGA-II算法在动车组列车多目标优化中的应用

2020-11-19汤旻安王茜茜蔚璠

铁道科学与工程学报 2020年10期

汤旻安，王茜茜, 2，蔚璠

汤旻安1，王茜茜1, 2，蔚璠1

(1. 兰州交通大学自动化与电气工程学院，甘肃兰州 730070；2. 兰州理工大学电气工程与信息工程学院，甘肃兰州 730050)

针对动车组列车运行需综合考虑准点、节能、安全、舒适的复杂问题，将运行时间视为旅客满意标准，能耗视为铁路公司的满意标准，同时考虑过电分相对列车运行的影响，使列车的运行更符合实际情况，建立列车运行多目标优化模型，该模型受安全性、轨道特点、乘客舒适度等的约束。提出一种NSGA-II算法与黄金比例技术相结合的算法，解决使用NSGA-II算法优化时个体在解空间中分配不均的问题，通过对算法的测试，表明黄金比例NSGA-II算法的分布性和收敛性比NSGA-II算法好。最后以武广客运专线中某一区段的线路CRH3型动车组为仿真实例，展示仿真的一些结果，进一步表明所建模型与所提算法是可行的。

黄金比例；NSGA-II；动车组列车；电分相；多目标优化

作为一种舒适和快速的交通系统，高速铁路已经成为最有效的交通方式之一。“复兴号”的运行，标志着中国高速动车组已处于世界领先地位，与此同时，列车的综合运行性能也需提出更高的标准，其运行的安全、正点、低能耗和舒适性均包括其中。因此，研究动车组列车的多目标优化问题，不但可使铁路自身可持续发展壮大，而且有很大的经济意义[1]。对于列车的多目标优化，Khmelnitsky[2]研究了任意限速下变坡曲线上的列车运行情况；Chang等[3]提出一种基于Pareto最优集的差分进化方法，对模糊控制器的隶属度函数参数进行多目标优化。Kim等[4]建立了时间驱动的列车性能仿真模型，研究了不同线路上的能耗变化情况与惰行点之间的关系。Domínguez等[5]提出一种多目标粒子群算法，获得ATO系统中的能耗/时间Pareto非劣解，兼顾了乘客的舒适性。余进等[6−7]分别以混合微粒群算法和改进的多目标微粒群算法解决列车多目标优化问题，获得了预期效果。徐凯等[8]融合了PSO算法与布谷鸟搜索方法，解决列车多目标优化问题，具有较好的优越性。李珊等[9]对区间最高运行速度和时间进行优化，考虑了运行图的编制，节能效果明显。此外，严细辉等[10−12]也对列车的多目标优化问题进行了研究。对于列车多目标优化问题，国内外学者已做了大量工作并取得诸多成果，但还存在以下问题：1) 很少考虑电分相对列车运行过程的影响；2) 单目标优化的最优解与多目标优化的最优解有本质差异，而大多研究将多目标优化最后转为单目标优化进行求解，如此只能提供单一解决方案，且各个目标函数量纲很难统一，加权值的分配带有较强的主观性，导致很多最优解的丢失，也降低了优化算法的收敛速度。传统的NSGA-II算法无法有效地识别伪非支配解，容易陷入局部最优，解集质量差，难以求得分布均匀的Pareto最优解。针对这些问题，赖文星等[13]提出一种基于支配强度的INSGA-DS改进算法，将其应用到飞机算例的仿真中，取得了良好效果。乔俊飞等[14]将差分变异算子引入到了NSGA-II算法中，改善了种群的分布性。姜慧兰等[15]借助正态分布交叉算子加强了NSGA-II算法的全局搜索能力，得到了最佳的电网规划方案。基于以上分析，本文对列车运行过程进行多目标优化，提出一种NSGA-II算法与黄金比例技术相结合的多目标优化方法，来解决NSGA-II算法在优化时出现解分布不均的情况，更能保证种群个体的多样性和求解质量，同时考虑电分相对列车运行的影响，使列车运行更符合实际情况，以此提供更加可行的解决方案，指导列车运行。

1 列车运行过程分析

1.1 受力分析

如图1所示，列车运行期间，受牵引力t()，制动力b()，基本阻力0()和线路附加阻力d(,)的共同作用，其牵引/制动性能由列车牵引/制动特性、编组质量和运行阻力共同决定。虽然动车组列车和普通列车之间有很多不同，但是列车的受力情况和运行特点都可以由牛顿第二运动定律进行分析。

列车受到的牵引力与制动力分别根据相应车型的牵引与制动特性曲线计算，所受基本阻力影响因素相当复杂，通常用经验公式进行计算

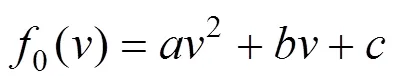
式中：v为列车速度；a，b和c为基本阻力系数。

附加阻力计算公式为

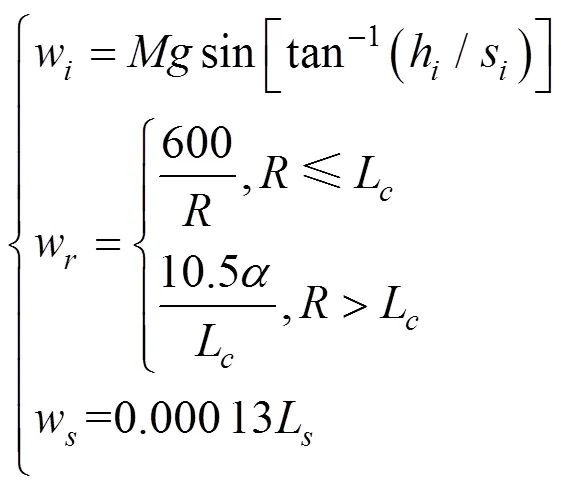
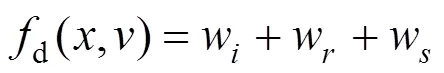
式中：w为坡道附加阻力；为列车质量，t；为重力加速度，取9.81 m/s2；h和s为改变的坡高和每个坡道的距离；w为曲线附加阻力；为曲线半径；为曲线中心角；L为列车长度；w为隧道附加阻力；L为隧道长度。

1.2 运动方程

基于以上分析，所有的运行工况和相应的受力情况应该集中到牵引建模过程中。因此，动车组列车的运动学模型可以写为

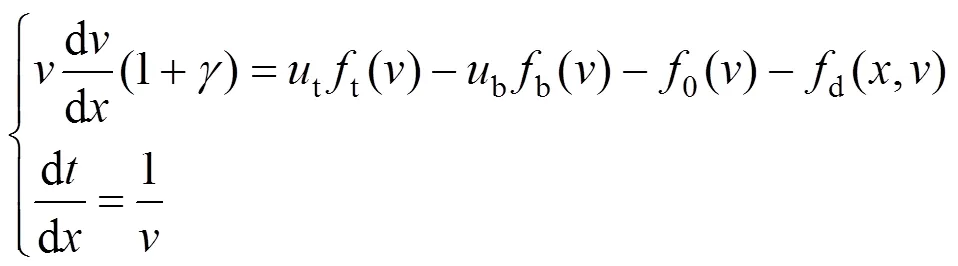
式中：γ为回转质量系数；x是从某一参考位置的运行距离；和表示牵引力使用系数和制动力使用系数。

典型的动车组列车运行过程可以划分为3个工况，即牵引、惰行和制动，而对于长距离运行线路，理论上存在最优的控制方案包括最大牵引、匀速、惰行和制动。图2显示2个相邻车站之间的速度−距离曲线。

列车从始发点到终点，有多种不同的操纵方式，按照规定的运行时间，可使用不同的运行工况，而不同运行工况的耗能、运行时间及舒适性等千差万别。因此，选取合理的运行工况对铁路公司和乘客都具有十分重要的意义。

2 多目标优化模型的构建

多目标优化不是让全部目标都取得最优解，而是在它们之间进行协调折中处理，使各个目标都尽可能地达到最优。由于无法求得最优解，这种情况下，通过离线仿真计算的方法获得优化操纵的数值规律，再与实时调整相结合以获得一些可行的满意解，是建立列车优化操纵实时指导系统合适的研究策略之一。

2.1 能耗模型

运行能耗包括给列车提供牵引动力的能耗、克服阻力所需的能耗和列车辅助设备能耗，运行能耗占总能耗的80%以上，因此降低运行能耗具有很大的价值。本文仅对列车牵引与制动过程及辅助设备所消耗的能量进行考虑。

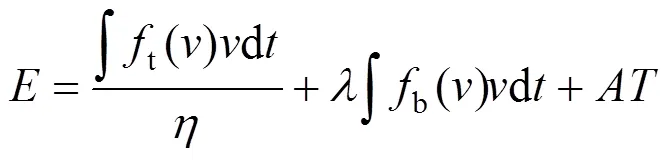
式中：为能耗利用率；为再生制动能量利用率；为列车辅助设备功率；为列车运行时间。

2.2 准点性

运行时间是列车从始发点到终点运行所需的时间，其与列车计划运行时间越接近，则准点性越高。

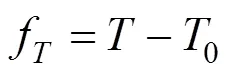
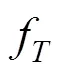
综上所述，列车运行的多目标优化可以表达为：根据列车运动模型，求出一组输入控制序列，以及控制转换地点，在满足列车运行安全、乘客舒适等的约束下，使得运行能耗和运行时间都尽可能达到最小。

列车多目标优化模型为

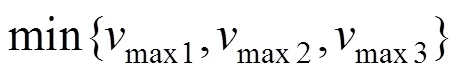
3 基于黄金比例NSGA-II算法的多目标优化

NSGA-II是基于Pareto概念的多目标遗传算法，是对NSGA的改进，将大小为的父代种群P与大小为的子代种群Q相结合，形成一个大小为2的新种群R，接着以多目标解为基础，将R逐层分类，再依照非支配关系及拥挤度大小关系对解个体进行排序操作，最后根据排序结果选择前个个体，形成新种群[16]。NSGA-II算法操作相对简单，优化速度快，可获得较好的解。

然而，NSGA-II在解决列车运行过程这类多目标优化问题时，随着优化目标数量和种群规模的增加，一部分个体不被支配，导致了支配关系不足以强化算法的收敛能力，往往会产生个体在解空间中分配不均的问题[17]，在一定程度上影响了求解质量。因此，本文提出一种基于黄金比例技术的NSGA-II算法，来优化此问题。

3.1 基于黄金比例技术的NSGA-II优化算法

3.1.1 黄金比例点的局部优化

黄金比例是一个数学比率关系，表现了内在的和谐与平衡。利用对称与相等收缩原理逐渐减小搜索范围，将解空间每次缩小到0.382或0.618倍，找到2个局部最优个体间的更优的个体。如图3所示，与是2个已确定的最优个体，为潜在的最优点，通过黄金比例可获得。′为应用反向原理，将旋转180°所得到的反向黄金比例局部最优位置，目的是为了拓宽算法解集的局部搜索空间[18]。

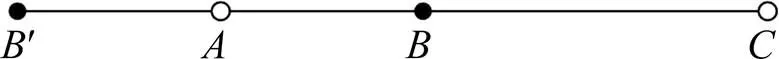
图3 黄金比例局部最优位置示意图

3.1.2 黄金比例NSGA-II算法

针对NSGA-II算法在进行列车运行多目标优化时存在个体在解空间中分配不均的问题，引入黄金比例技术，对NSGA-II算法进一步改进，其核心步骤如下。

1) 子代种群Q的产生过程

随机产生初始种群P和P，P是算法全局优化的主种群，P是黄金比例局部优化的子种群。采用Metropolis准则概率接受P中的新个体，替换P中最差的个体。然后从每代遗传算法优化过的个体中选择最好的2个个体，更新P中的个体，并从P中选择个优秀个体作为初始个体，使用黄金比例算子执行局部优化。该过程引入黄金比例概率0.382或0.618搜索最优自适应点，提升搜索效率，加快运算。相应的交叉和变异概率为

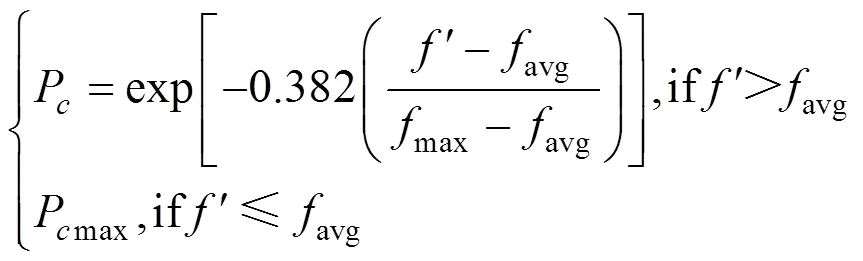
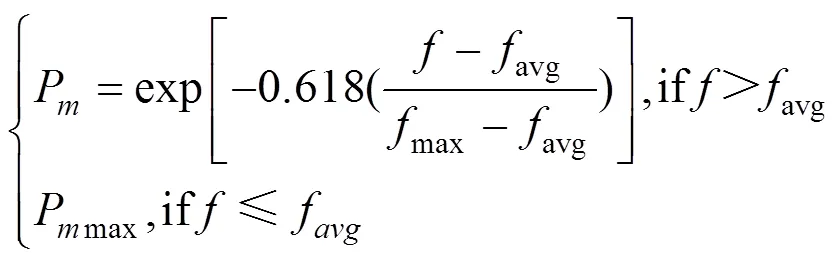
式中：avg为平均适应度值；max为最大适应度值；′为2个交叉个体间较大的适应度值；为要变异的个体适应度值；Pmax为最大交叉概率；Pmax为最大变异概率。通过以上操作，产生子代种群Q。

2) 组合种群R的处理

①设各个点的拥挤度i为0；

③计算其余个体的拥挤度：

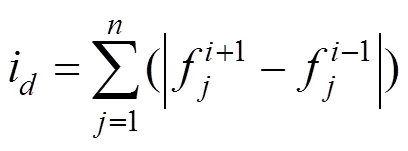
3.2 用黄金比例NSGA-II算法对模型求解

3.2.1 电分相对列车运行的影响

动车组列车的运行要经过电分相区段。为使列车的运行更符合实际情况，因此考虑电分相对列车运行的影响。若不考虑电分相，则很有可能将因降弓断电而无牵引力的状况，错误地操纵为牵引运行，导致仿真优化结果与列车的实际运行情况截然不同。本文假设采用惰行方式过电分相，即列车过电分相时采用固定的操纵工况。

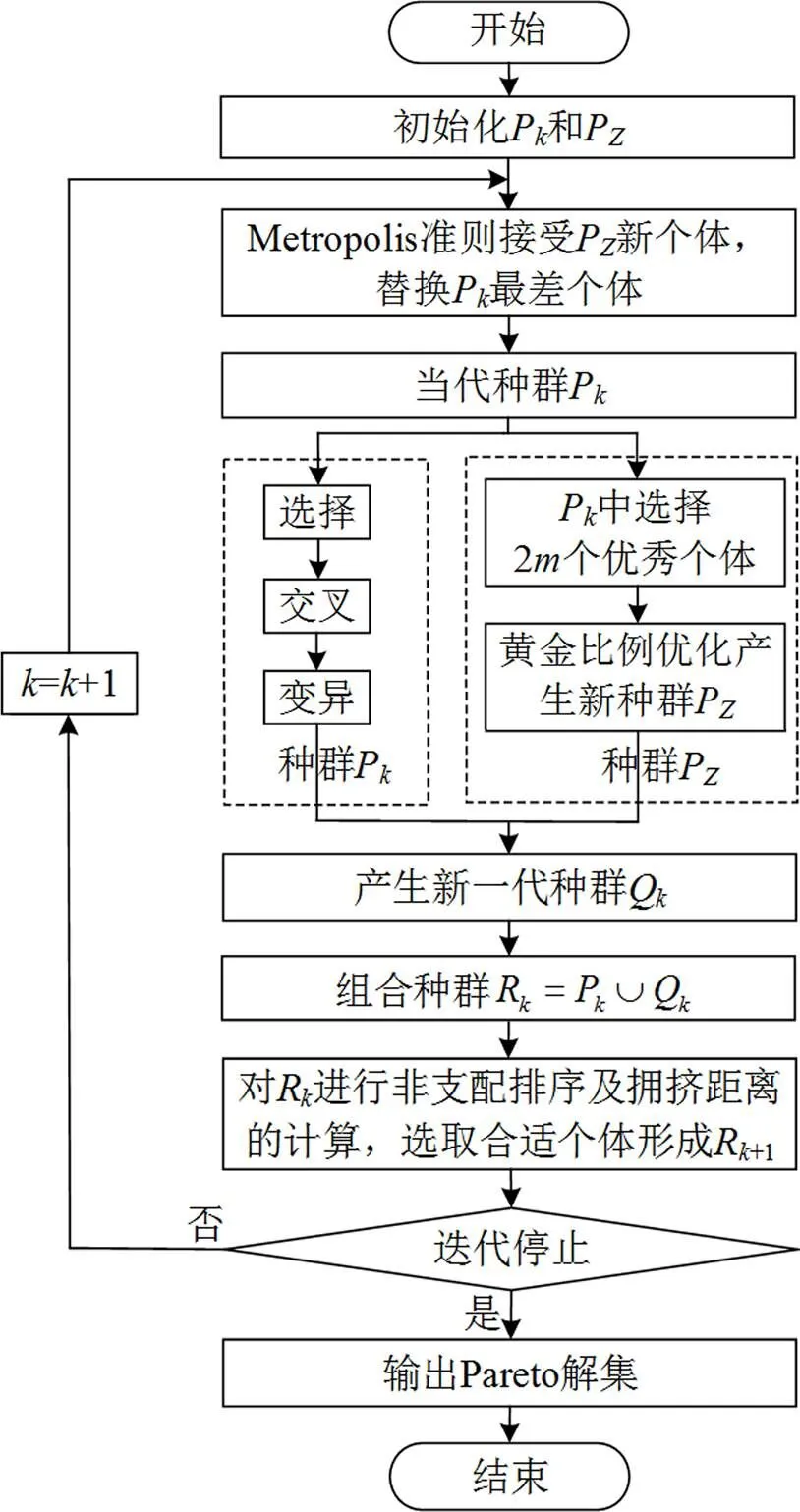
图4 黄金比例NSGA-II算法流程图

使用黄金比例NSGA-II算法优化时，将电分相工况作为基因包含于染色体中。在进行交叉和变异操作时，由于会随机选择交叉点和变异点，当选中电分相区段内的基因时，有可能产生不可行解。因此：在全局及局部优化之前进行判断，使电分相区段内的基因不参与优化操作。

3.2.2 用黄金比例NSGA-II算法对模型求解

使用黄金比例NSGA-II算法对所建列车多目标优化模型进行求解的具体步骤如下。

1) 输入基本仿真数据和相应参数。输入线路数据、列车数据及算法相关参数，将变量离散化。

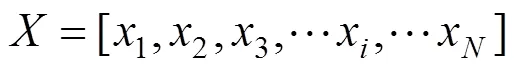
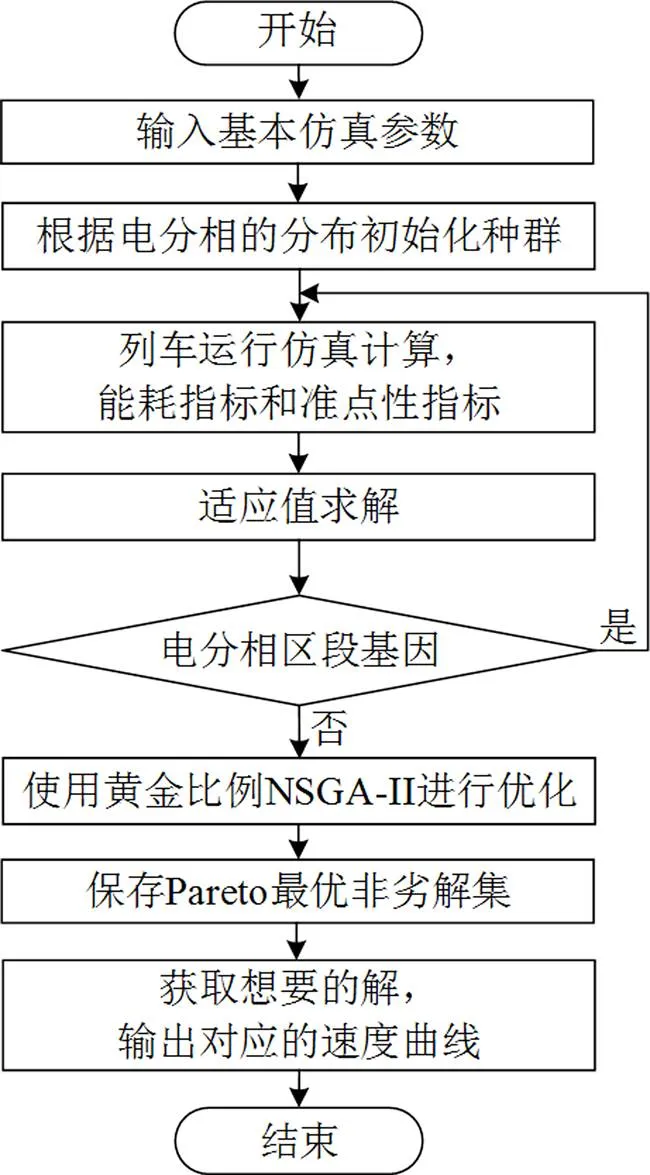
图5 列车多目标优化模型求解的流程图

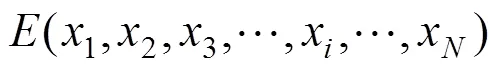
4) 根据黄金比例NSGA-II算法核心步骤1)，产生子代种群Q。

5) 产生新的父代种群。根据黄金比例NSGA-II算法核心步骤2)，产生新的父代种群R。

6) 判断是否达到停止条件，没有则转入步骤3)，直到满足停止条件，保存相应的Pareto非劣解集。

7) 获取想要的解。取Pareto非劣解集中准点性最好的解作为想要的解，提取相应的速度-距离曲线。根据以上步骤，用黄金比例NSGA-II算法对所建列车多目标优化模型进行求解的流程图如图5 所示。

4 算法实例仿真分析

4.1 算法性能测试

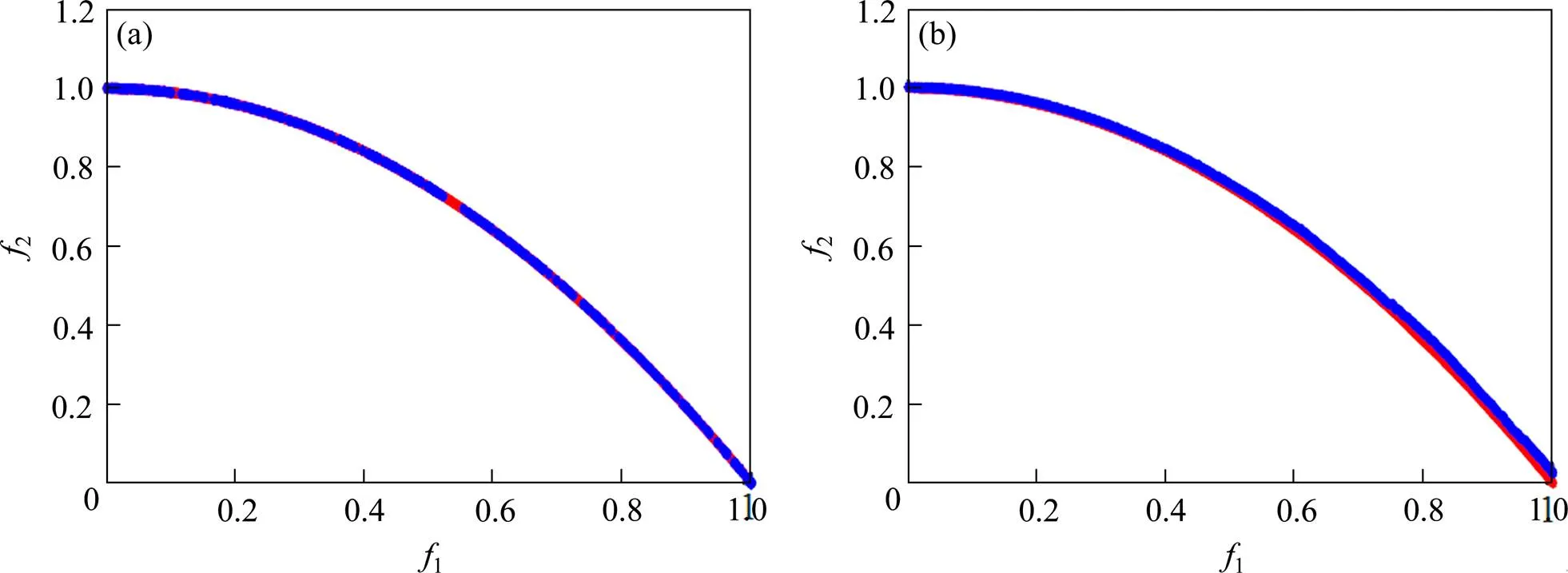
多目标算法优化的目的不仅是使种群均匀分布于Pareto前沿，而且要快速收敛，因此为了定量地分析2种算法的优劣性，选取测试函数ZDT1~ ZDT4[19]进行仿真。NSGA-II算法运行参数设置为：种群规模为200，运行代数为300，交叉概率为0.9，变异概率为0.01；黄金比例NSGA-II算法参数设置为：局部优化种群规模2=40，Pmax=0.9，Pmax=0.1，其他参数与NSGA-II算法中相同。2种算法针对ZDT1~ZDT4的最优Pareto前沿如图6~9所示。以分布性指标SP[20]和收敛性指标GD[21]作为评价准则，对2种算法的性能进行对比。其中SP和GD的计算公式为

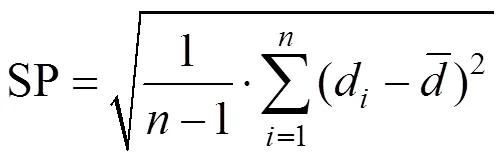
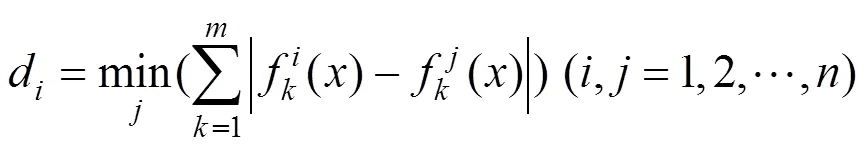
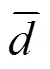
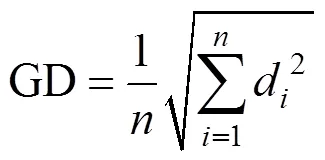
式中：为解的数目；d是第个个体距离已知的Pareto前沿中所有个体的欧式距离的最小值。GD的值越小说明解集越靠近Pareto最优解集。

(a) NSGA-II；(b) 黄金比例NSGA-II

图6 ZDT1的Pareto前沿

Fig. 6 Pareto frontier of ZDT1

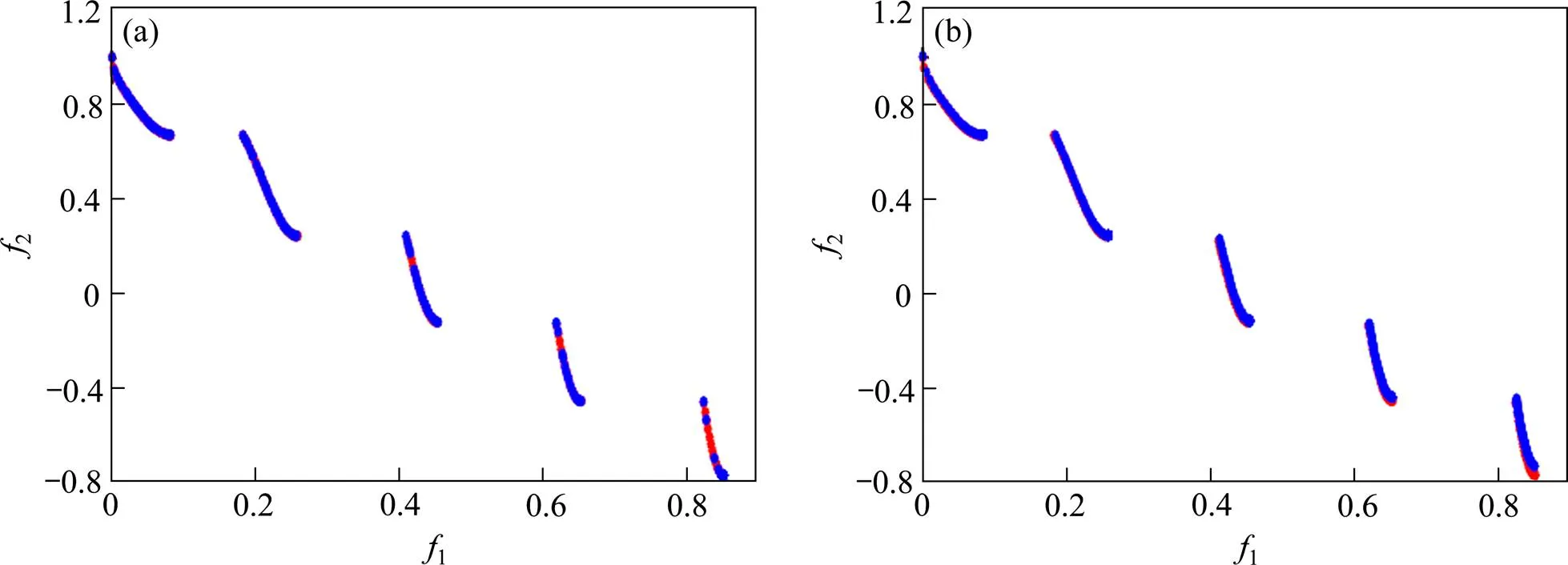
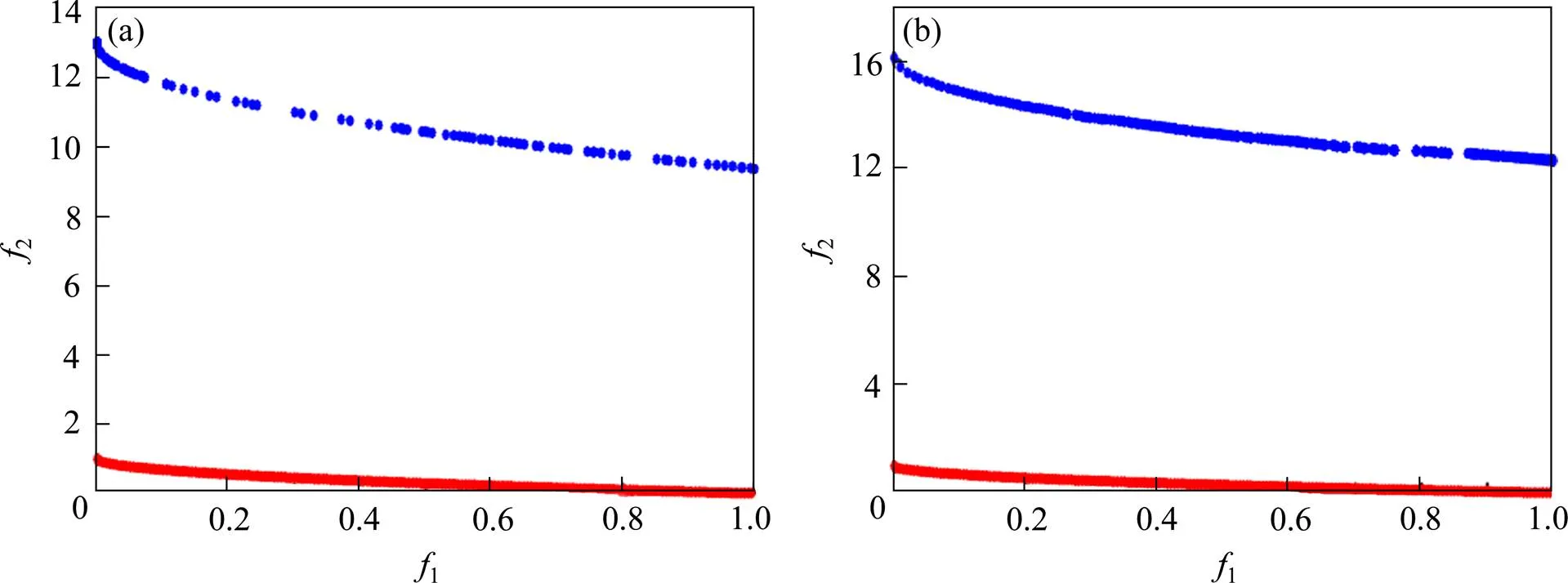
(a) NSGA-II；(b) 黄金比例NSGA-II

将NSGA-II算法与黄金比例NSGA-II算法各执行10次，10次计算所得的SP和GD的平均值如表1所示。

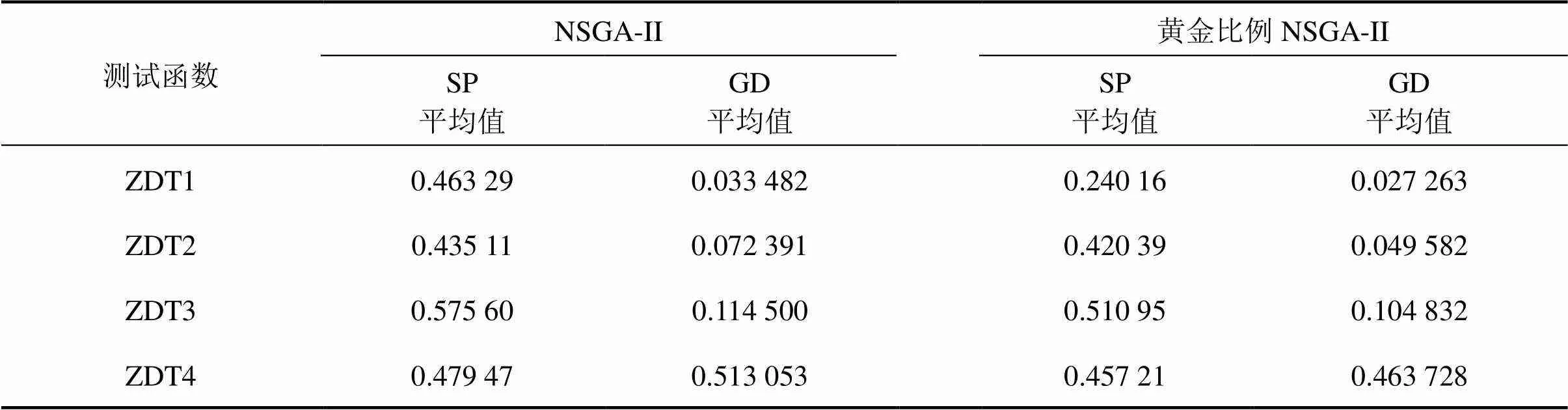
表1 算法性能对比

由对比可知，黄金比例NSGA-II算法所求得的SP均值比NSGA-II算法所求得的SP均值大，且所求得的GD均值也大于NSGA-II算法所求得的GD均值，说明黄金比例NSGA-II算法比NSGA-II算法在Pareto前沿分布均匀性方面好，在算法收敛性上也有所改善。

4.2 列车运行多目标优化实例仿真

以武广客运专线中武汉到新乌龙泉区段的线路作为仿真实例[22]，线路总长47.646 km，含25个坡道、6段曲线和2处电分相，分相区为16.177～16.819 km和40.079～40.705 km。线路限速情况如表2所示。设置运行时间1 050 s，时间裕量60 s。选4动4拖的CRH3动车组列车，其主要参数如表3所示。

表2 线路限速情况

表3 CRH3主要参数特性

使用NSGA-II算法与黄金比例NSGA-II算法分别对列车多目标优化模型进行求解，2种算法参数设置与4.1节中相同，优化所得到的Pareto前沿面分别如图10和图11所示。

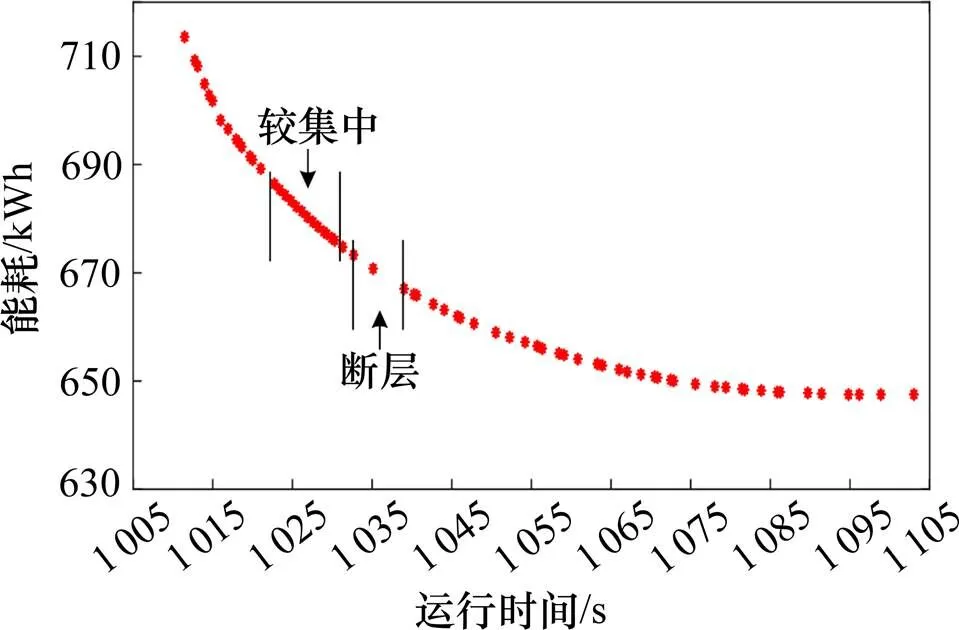
图10 NSGA-II算法的Pareto前沿

由图10和图11中的解集分布情况可看到，2种算法都能较好地搜索到Pareto曲线上的点，但NSGA-II算法所求得的解集分布在1 028~1 035 s处出现断层的现象，在1 019~1 026 s间较集中，而黄金比例NSGA-II算法所求得的解集分布更加均匀，搜索能力更强。2种算法在列车多目标优化中的运行结果比较如表4所示。

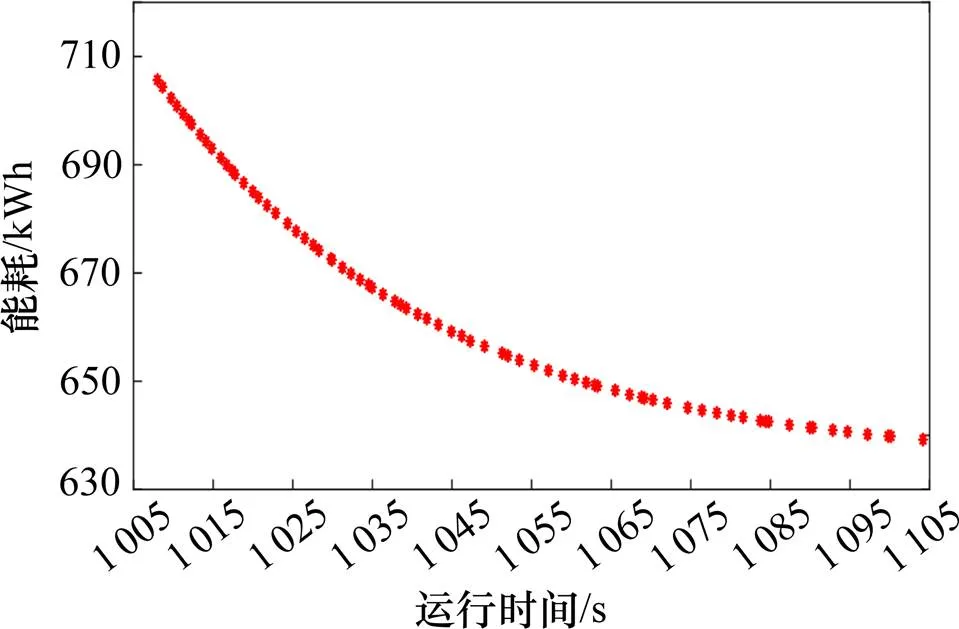
图11 黄金比例NSGA-II算法的Pareto前沿

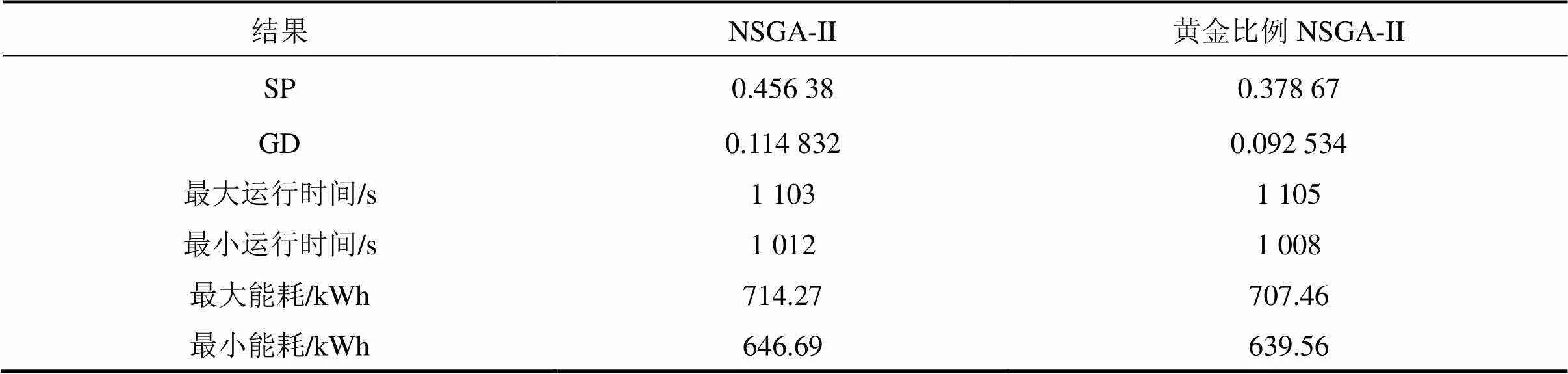
表4 2种算法结果比较

由表4可知，黄金比例NSGA-II算法的SP值与GD值都小于NSGA-II算法。在都满足列车准点性的要求下，所求得的最小能耗比NSGA-II算法求得的最小能耗小，这是因为有了黄金比例的搜索，有助于更精准地挑选出优良个体，使算法的优化更趋于全局优化。由此可知，黄金比例NSGA-II算法在列车多目标优化中得出的解集更优秀，综合优化性能更好。

输出2种算法所求解集中准点性最好的解的速度−距离曲线如图12所示，其中算法1表示黄金比例NSGA-II算法，算法2表示NSGA-II算法。

由图12可以看到，2种算法优化的列车最准点速度曲线全程均没有出现超速现象，也均到达终点，因此满足安全性和精确停车约束。在NSGA-II算法优化和黄金比例NSGA-II算法优化中，均考虑了电分相对列车运行的影响，列车在过两处电分相时均为惰行工况，符合列车实际运行情况。

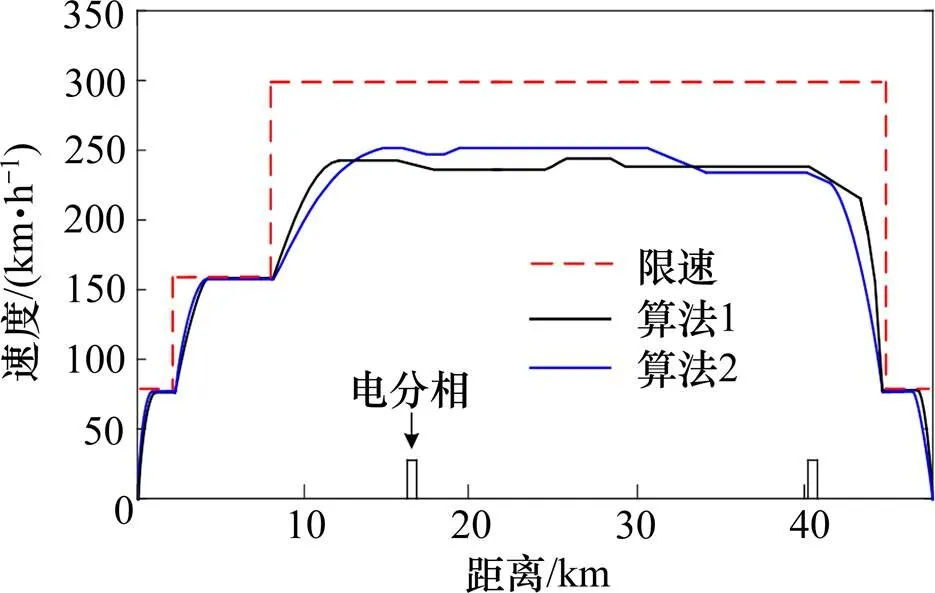
图12 列车速度轨迹

经计算，2条速度曲线对应的能耗和运行时间如表5所示。

表5 运行结果

可以看出，在黄金比例NSGA-II所优化的最准点运行时间比NSGA-II所优化的最准点运行时间少了2.3 s，而且运行能耗节约了0.97%。

5 结论

1) 在动车组列车多目标优化运行控制中，本文考虑过电分相这个特殊的环节，使列车的运行更加符合实际情况。

2) 设计了一种黄金比例NSGA-II算法，来解决使用NSGA-II算法进行优化时个体在解空间分配不均的问题。由算法的性能测试结果可知，黄金比例NSGA-II算法在收敛性和分布性上都比NSGA-II算法好，说明引入的黄金比例技术是有效的。

3) 由列车运行实例仿真分析可知，黄金比例NSGA-II算法对列车运行能耗、准点性方面都有一定的优化效果，可以兼顾动车组列车的安全、准点和低能耗运行。使用黄金比例NSGA-II算法进行优化，以此丰富决策者的选择，为列车的运行提供更加真实可行的速度曲线。

本文的列车多目标优化对象为单列车，而列车在运行时会受到前后运行的列车的影响，后续可研究列车的追踪运行，以适应列车动态变化的运行情况，达到更好的指导效果。

[1] 唐涛, 黄良骥. 列车自动驾驶系统控制算法综述[J]. 铁道学报, 2003, 25(2): 98−102. TANG Tao, HUANG Liangji. A survey of control algorithm for automatic train operation[J]. Journal of the China Railway Society, 2003, 25(2): 98−102.

[2] Khmelnitsky E. On an optimal control problem of train operation[J]. IEEE Transactions on Automatic Control, 2000, 45(7): 1257−1266.

[3] Chang C S, Xu D Y, Quek H B. Pareto-optimal set based multiobjective tuning of fuzzy automatic train operation for mass transit system[J]. IEEE Proceedings -Electric Power Applications, 1999, 146(5): 577−583.

[4] Kim K , Chien I J. Simulation-based analysis of train controls under various track alignments[J]. Journal of Transportation Engineering, 2010, 136(11): 937−948.

[5] Domínguez M, Fernández-Cardador A, Cucala A P, et al. Multi objective particle swarm optimization algorithm for the design of efficient ATO speed profiles in metro lines[J]. Engineering Applications of Artificial Intelligence, 2014, 29(3): 43−53.

[6] 余进, 何正友, 钱清泉. 基于混合微粒群优化的多目标列车控制研究[J]. 铁道学报, 2010, 32(1): 38−42. YU Jin, HE Zhengyou, QIAN Qingquan. Study on multi- objecive train control based on hybrid particle swarm optimization[J]. Journal of the China Railway Society, 2010, 32(1): 38−42.

[7] 余进, 何正友, 钱清泉. 基于微粒群算法的多目标列车运行过程优化[J]. 西南交通大学学报, 2010, 45(1): 70−75. YU Jin, HE Zhengyou, QIAN Qingquan. Multi-objecive train operation optimization based on particle swarm optimization[J]. Journal of Southwest Jiaotong University, 2010, 45(1): 70−75.

[8] 徐凯, 吴磊, 杨飞凤. PSO-ICS算法优化的城轨列车自动驾驶系统[J]. 铁道科学与工程学报, 2017, 14(12): 2704−2712. XU Kai, WU Lei, YANG Feifeng. Automatic train operation system in urban rail transit based on PSO-ICS algorithm optimization[J]. Journal of Railway Science and Engineering, 2017, 14(12): 2704−2712.

[9] 李姗, 苗建瑞, 孟令云, 等. 面向节能的城轨列车区间运行时分优化研究[J]. 铁道科学与工程学报, 2016, 13(8): 1630−1635. LI Shan, MIAO Jianrui, MENG Lingyun, et al. Optimization of urban rail transit segment running time based on energy saving[J]. Journal of Railway Science and Engineering, 2016, 13(8): 1630−1635.

[10] 严细辉, 蔡伯根, 宁滨, 等. 基于差分进化的高速列车运行操纵的多目标优化研究[J]. 铁道学报, 2013, 35(9): 65−71. YAN Xihui, CAI Baigen, NING Bin, et al. Research on multi-objective high-speed train operation optimization based on differential evolution[J]. Journal of the China Railway Society, 2013, 35(9): 65−71.

[11] SHANGGUAN Wei, YAN Xihui, CAI Baigen, et al. Multiobjective optimization for train speed trajectory in CTCS high-speed railway with hybrid evolutionary algorithm[J]. IEEE Transactions on Intelligent Transportation Systems, 2015,16(4): 2215−2225.

[12] 高浠瑞, 董海鹰, 杨立霞. 高速列车追踪运行的多目标优化研究[J]. 铁道科学与工程学报, 2016, 13(12): 2335−2340. GAO Xirui, DONG Haiying, YANG Lixia. Research on multi-objective optimization for tracking operation of high-speed train[J]. Journal of Railway Science and Engineering, 2016, 13(12): 2335−2340.

[13] 赖文星, 邓忠民, 张鑫杰. 基于多目标优化NSGA2改进算法的结构动力学模型确认[J]. 计算力学学报, 2018, 35(6): 669−674. LAI Wenxing, DENG Zhongmin, ZHANG Xinjie. Structural dynamics model validation based on NSGA2 improved algorithm[J]. Chinese Journal of Computational Mechanics, 2018, 35(6): 669−674.

[14] 乔俊飞, 魏静, 韩红桂. 基于改进NSGA2算法的给水管网多目标优化设计[J]. 控制工程, 2016, 23(12): 1861−1866. QIAO Junfei, WEI Jing, HAN Honggui. Multi-objective optimization of water distribution system based on an improved NSGA2 algorithm[J]. Control Engineering of China, 2016, 23(12): 1861−1866.

[15] 姜惠兰, 安星, 王亚微, 等. 基于改进NSGA2算法的考虑风机接入电能质量的多目标电网规划[J]. 中国电机工程学报, 2015, 35(21): 5405−5411. JIANG Huilan, AN Xing, WANG Yawei, et al. Improved NSGA2 algorithm based multi-objective planning of power grid with wind farm considering power quality[J]. Proceedings of the CSEE, 2015, 35(21): 5405−5411.

[16] Deb K. A fast and elitist multi-objective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182−197.

[17] 丁圣. 基于NSGA-Ⅲ的列车多目标操纵优化研究[D].北京: 北京工业大学, 2018. DING Sheng. Study on optimization of multi-objective maneuvering of trains based on NSGA-Ⅲ[D]. Beijing: Beijing University of Technology, 2018.

[18] 杨文臣, 张轮, 饶倩, 等. 基于黄金分割点遗传算法的交通信号多目标优化[J]. 交通运输系统工程与信息, 2013, 13(5): 48−55. YANG Wenchen, ZHANG Lun, RAO Qian, et al. Multi-objective optimization for traffic signals with golden ratio based on genetic algorithm[J]. Journal of Transportation Systems Engineering and Information Technology, 2013, 13(5): 48−55.

[19] 栗三一, 李文静, 乔俊飞. 一种基于密度的局部搜索NSGA2算法[J]. 控制与决策, 2018, 33(1): 60−66. LI Sanyi, LI Wenjing, QIAO Junfei. A local search strategy based on density for NSGA2 algorithm[J]. Control and Decision, 2018, 33(1): 60−66.

[20] Schott J R. Fault tolerant design using single and multicriteria genetic algorithm optimization[D]. Cambridge: Massachusetts Institute of Technology, 1995.

[21] Deb K, Jain S. Running performance metrics for evolutionary multi-objective optimization[R]. Kanpur: Indian Institute of Technology, 2002.

[22] 纪云霞. 列车节能运行优化的改进遗传算法研究[D]. 成都: 西南交通大学, 2018. JI Yunxia. Study on improved genetic algorithm for train energy-saving operation optimization[D]. Chengdu: Southwest Jiaotong University, 2018.

Application of golden ratio NSGA-II algorithm in multi-objective optimization of EMU trains

TANG Minan1, WANG Qianqian1, 2, YU Fan1

(1. School of Automation and Electrical Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China;2. School of Electrical Engineering and Information Engineering, Lanzhou University of Technology, Lanzhou 730050, China)

Aiming at the complex problem that the EMU (Electric Multiple Units) trains operation need to consider punctuality, energy saving, safety and comfort, the operation time was regarded as the standard of passenger satisfaction, and the energy consumption was seen as the standard of the railway company satisfaction. Meanwhile, considering the influence of electrical phases in order to make the train operation more in line with the actual situation, a multi-objective optimization model for the train operation was established, which was constrained by safety, track characteristics and passenger comfort and so on. Then, a kind of algorithm combining NSGA-II (Non-dominated Sorting Genetic Algorithm-II) with golden ratio technology was proposed to solve the problem of uneven individuals distribution in the solution space when using NSGA-II to optimize. The tests of the algorithms show that the golden ratio NSGA-II algorithm has better distribution and convergence than the NSGA-II algorithm. Finally, taking CRH3of a certain section of Wuhan-Guangzhou line as a simulation case, some simulation results are shown, which further indicate that the model and the proposed algorithm are feasible.

golden ratio; NSGA-II; EMU trains; electrical phases; multi-objective optimization