静电场中“三线”问题的解题策略
2020-11-16湖北胡卫雄
湖北 胡卫雄
一、问题的提出
本文中所说的“三线”是指电场线、等势线(面)和带电粒子在电场中的运动轨迹。
“三线”问题往往将电场线、等势线(面)和粒子运动的轨迹相结合,考查学生应用静电场知识(电场强度、电场线、静电力、静电力做功、电势能、电势、电势差、等势面等)和力学知识(牛顿运动定律、动力学关系、功能关系、能量守恒定律等)综合分析问题的能力。考查电场、静电力、电势能等物理观念,点电荷、电场等物理模型,进行科学推理的科学思维以及严谨求实的科学态度等核心素养,常以选择题形式出现。
二、问题解决的解题策略
“三线”问题往往设置以“三线”为载体的问题情境,要求在理解“三线”特征的基础上,按照以下“一二三四五”策略依次展开对问题的综合分析:
1.选择一个交点:在电场线和运动轨迹问题中,选择电场线和运动轨迹的一个交点位置去分析;在等势线(面)和运动轨迹问题中,选择等势线(面)和运动轨迹的一个交点位置展开分析。
2.抓住两个关键:确定速度方向和静电力方向是解决问题的两个关键,需要画出“速度方向线”(运动轨迹在交点位置的切线)与“静电力方向线”(在交点位置电场线的切线方向,指向轨迹的凹侧)。
3.确定三个要素:在“三线”问题中电荷的正负、电场线的方向,电荷运动方向,是题目中相互制约的三个要素。如三个要素不明确的,则要用“假设法”分别讨论各种情况。
4.掌握四类方法:要根据加速度大小的判断方法、速度大小的判断方法、静电力做功正负的判断方法、电势能增减与电势高低的判断方法等四种方法对常见的问题做出判断。
5.明确五组关系:分析“三线”问题要明确以下五组关系,即
(1)电荷电性、电场强度方向、静电力方向的关系
正电荷受到的静电力方向与电场强度方向相同;负电荷受到的静电力方向与电场强度方向相反。
(2)电荷电性、电势、电势能的关系
正电荷在电势高的位置电势能大,在电势低的位置电势能小;负电荷在电势高的位置电势能小,在电势低的位置电势能大。
(3)电场线和等势面关系
等势面一定与电场线垂直,电场线方向总是从电势高的的等势面指向电势低的等势面;等差等势面越密的地方电场强度越大,反之越小。
(4)力与运动关系
带电粒子做曲线运动,则所受合力(往往仅为静电力)应指向轨迹曲线的凹侧,轨迹夹在力和速度方向之间。
(5)做功和能量转化关系
静电力做功与电势能变化的关系,合力做功与动能变化的关系。
三、问题设置的途径
“三线”问题的设置主要有三类情境,每类情境又可分非典型电场和典型电场两种情形。在非典型电场中,在电荷电性、运动轨迹方向、电场线方向均未知的情况下,往往需要分情况讨论,先假设其中一种情况再依次分析。在典型电场中,根据典型电场的特点,可以推测电场的场强、电势和场源电荷的相关信息。
1.电场线和带电粒子的轨迹问题
(1)非典型电场
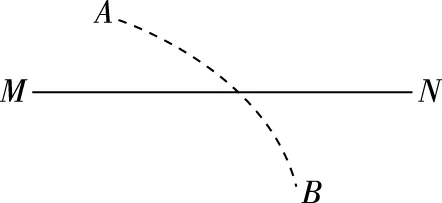
【例1】如图1所示,实线表示某电场的电场线(方向未标出),虚线是一带负电的粒子只在电场力作用下的运动轨迹,设M点和N点的电势分别为φM、φN,粒子在M和N时加速度大小分别为aM、aN,速度大小分别为vM、vN,电势能分别为EpM、EpN。下列判断正确的是
( )
A.vM C.φM<φN,EpM 图1 【分析】先选择带电粒子的轨迹和电场线的一个交点如图2所示,因不知道运动轨迹的方向这个要素,需要用假设法讨论从M到N或从N到M两种情况,确定如图2和3所示的两种情况下的速度方向和受到的合力方向,应用动力学关系、功能关系可判断,从M到N,速度、动能减小,从N到M,速度、动能增大,结果都是M点的动能、速度比N点的动能、速度大。结合能量守恒定律可知M点比N点的电势能小。再依据电荷电性、电势、电势能的关系判断M、N点的电势高低。由N、M处电场线的疏密判断电场强度的大小,比较静电力的大小,再由牛顿第二定律得到加速度大小关系。 图2 【解析】N点的电场线比M点的电场线更密集,所以电场强度更大,静电力更大,粒子的加速度也更大,aN>aM。若粒子从M运动到N,如图2所示,根据动力学关系,带电粒子所受电场力指向轨迹弯曲的内侧,可知在该点的电场力方向和速度方向成钝角,故电场力做负功,电势能增大,动能减小,即vM>vN,EpM (2)典型电场 【例2】如图4所示,在点电荷Q产生的电场中,实线MN是一条方向未标出的电场线,虚线AB是一个电子只在静电力作用下的运动轨迹。设电子在A、B两点的加速度大小分别为aA、aB,电势能分别为EpA、EpB。下列说法正确的是 ( ) A.电子一定从A向B运动 B.若aA>aB,则Q靠近M端且为正电荷 C.无论Q为正电荷还是负电荷一定有EpA D.B点电势可能高于A点电势 图4 【分析】根据曲线运动的动力学关系确定交点处静电力的方向向左(如图5所示),因为电子带负电,再根据电荷电性、静电力方向和电场强度方向关系确定电场线的方向向右。本题的关键是题目给出的是典型的点电荷电场,再结合点电荷的场强方向大小分布特点判断,如果场源电荷带正电,则应靠近M端,且从M到N电场强度变小,如果场源电荷带负电,则应靠近N端,且从M到N电场强度变大。运动轨迹的方向不明确,可用假设法讨论电子从A到B或从B到A的两种可能,均可符合题意,因而是不确定的。 图5 【解析】由于运动路径的方向不知,因此速度方向也不能确定,由所知条件无法判断电子的运动方向,故选项A错误;电子在电场中做曲线运动,虚线AB是电子只在静电力作用下的运动轨迹,电场力沿电场线指向曲线的凹侧,所以电子受到的静电力方向向左,电场强度方向向右,电场线方向向右,若aA>aB,说明电子在M点受到的电场力较大,M点的电场强度较大,根据点电荷的电场分布可知,靠近M端为场源电荷的位置,应带正电,故选项B正确;无论Q为正电荷还是负电荷,沿电场线方向电势降低,一定有电势φA>φB,电子电势能Ep=-eφ,电势能是标量,所以一定有EpA 2.等势面和带电粒子的轨迹问题 解答该类问题,可以先根据等势面与电场线互相垂直,由已知的等势面画出对应的电场线,将等势面和带电粒子的运动轨迹问题转化为电场线和带电粒子的运动轨迹问题。 (1)非典型电场 【例3】如图6所示,虚线a、b、c表示电场中的三个等势面与纸平面的交线,且相邻等势面之间的电势差相等。实线为一带正电荷的粒子仅在电场力作用下通过该区域时的运动轨迹,M、N是这条轨迹上的两点,则下列说法中正确的是 ( ) 图6 A.三个等势面中,a的电势最高 B.对于M、N两点,通过M点时电势能较大 C.对于M、N两点,通过M点时动能较大 D.带电粒子由M运动到N时,加速度增大 【分析】首先根据等势面和电场线垂直的关系,画出运动轨迹和等势面b的交点的电场线,将等势面、运动轨迹问题转化为如图7所示的电场线、运动轨迹问题。确定交点处的静电力方向和两个可能的速度方向,因为粒子带正电,可判断电场强度的方向如图8所示,根据电荷电性、电势高低、电势能大小的关系判断M点和N点电势能的大小,再依据能量守恒定律比较M点和N点的动能的大小,根据等势面的密集程度与电场强度的大小关系判断N点的电场强度比M点大。 图7 图8 【解析】画出运动轨迹与b等势线的交点处的一条电场线,由于带电粒子做曲线运动,所受电场力的方向必定指向轨道的凹侧,且和等势面垂直、电场线相切,因为电荷为正,所以电场线方向是由c指向b再指向a如图8所示。根据电场线的方向指向电势降低的方向,故φc>φb>φa,选项A错。正电荷在电势高处电势能大,M点的电势比N点电势低,故粒子在M点电势能小,选项B错。根据能量守恒定律,电荷的动能和电势能之和保持不变,故粒子在M点的动能较大,选项C正确。由于相邻等势面之间电势差相等,因N点等势面较密,则EN>EM,即qEN>qEM。由牛顿第二定律知,带电粒子从M点运动到N点时,加速度增大,选项D正确。 (2)典型电场 【例4】如图9所示,一带电粒子在两个固定的等量正电荷的电场中运动,图中的实线为等势面,虚线ABC为粒子的运动轨迹,其中B点是两点电荷连线的中点,A、C位于同一等势面上。下列说法正确的是 ( ) 图9 A.该粒子可能带正电 B.该粒子经过B点时的速度最大 C.该粒子经过B点时的加速度一定为零 D.该粒子在B点的电势能小于在A点的电势能 【分析】由图9所示的典型的等量同种正电荷等势面分布特点可知,从A到B点电势是先增加再降低,A点的电势低于B点的电势。等量同种正电荷的连线的中点B点电场强度为零。另外,由曲线运动的动力学关系可知,带电粒子在等势面和运动轨迹的交点A处受到的静电力方向指向轨迹内侧,所以带电粒子带负电。 【解析】从该带电粒子的运动轨迹判断静电力方向,由固定电荷带正电可知,该粒子一定带负电,故选项A错误;根据等量同种正电荷电势分布特点,因为粒子从A运动到B的过程中,电势先升高后降低,又该粒子带负电,所以电势能先减小后增加,根据能量守恒定律知,动能先增加后减小,故B点的动能不是最大,则经过B点时的速度不是最大,故选项B错误;B点是两点电荷连线的中点,合场强为零,故粒子受力为零,则加速度为零,故选项C正确;因为离正电荷越远,电势越低,即φA<φB,因粒子带负电,由Ep=φq得,EpA>EpB,故选项D正确。 3.“等势(线)面”问题——电场线和等势线(面)问题 这类问题一般设置典型电场的等势线(面)情景。根据等势面和电场线的关系,画出相对应的电场线,把此类问题转化成电场线和等势面(线)问题。在分析中要注意典型电场的电场强度和电势分布特点,依据动力学关系画出运动轨迹。 【例5】两个固定的等量异号点电荷所产生电场的等势面如图10中虚线所示,一带负电的粒子以某一速度从图10中A点沿图示方向进入电场在纸面内飞行,最后离开电场,粒子只受静电力作用,则粒子 ( ) A.做直线运动,电势能先变小后变大 B.做直线运动,电势能先变大后变小 C.做曲线运动,电势能先变小后变大 D.做曲线运动,电势能先变大后变小 图10 【分析】先根据题目给定的典型电场——等量异号点电荷的电场等势面画出该电场的电场线如图11所示,粒子带负电,所以静电力方向与电场强度方向相反,依据力与运动的关系定性的画出带电粒子的运动轨迹如图11所示,可知粒子在运动过程中电势先升高后降低,再依据电荷电性、电势、电势能的关系判断电势能的变化。 图11 【解析】两固定的等量异号点电荷的电场分布如图11所示。带负电的粒子以速度v进入电场后,电场力的方向与v的方向不在一条直线上,故带负电的粒子做曲线运动,运动轨迹如图11所示,故选项AB错误。带负电的粒子先由低电势面运动到高电势面,然后由高电势面运动到低电势面,所以电势能先减小后增大,故选项C正确,选项D错误。 【例6】(2018年全国卷Ⅰ)图12中虚线a、b、c、d、f代表匀强电场内间距相等的一组等势面,已知平面b上的电势为2 V。一电子经过a时的动能为10 eV,从a到d的过程中克服电场力所做的功为6 eV。下列说法正确的是 ( ) A.平面c上的电势为零 B.该电子可能到达不了平面f C.该电子经过平面d时,其电势能为4 eV D.该电子经过平面b时的速率是经过d时的2倍 图12 图13 【解析】匀强电场中等势面间距相等,相邻等势面之间的电势差相等。电子从a到d的过程中克服电场力做功为6 eV,电场方向水平向右,画出电场线,Uad=6 V,又b等势面电势为2 V,所以c等势面电势为零,a等势面电势为4 V,d等势面电势为-2 V,电子经过平面d时,其电势能为2 eV,选项A正确,选项C错误。题目没有给出电子运动的初速度方向,所以运动轨迹不能判断,有可能到达不了平面f,选项B正确,根据动能定理,电子经过平面b时,动能为8 eV,电子经过平面d时,动能为4 eV,该电子经过平面b时的动能是经过d时动能的2倍,故选项D错误。