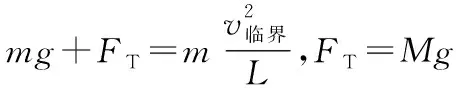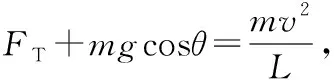圆周运动中临界极值情境与赋值间的关系
2020-11-16安徽
安徽 邵 永
物理中的临界极值问题无论是否出现“恰好”“不脱离”“最大”“至少”等词语,总会隐去或者部分隐去研究对象的现象,且有一定的变化条件,在变化过程中使得某些物理量达到最大或最小,从一种现象变为另一种现象。这类问题往往具有情景隐蔽、过程复杂的特点,主要考查受力分析、运动分析、功能关系等物理学科主干知识和利用数学知识处理物理问题的能力,做到基础与能力并重、基础与素养兼容。在教学过程中把一定的物理模型进行变式分析,或对相同的物理模型给予不同赋值,对其临界极值情境进行对比分析,均能培养学生的理性思维能力,加深学生对所学知识的深刻理解和应用,针对试题做到有的放矢。
一、水平面内匀速圆周运动中的临界极值问题
【例1】如图1所示,A、B、C三个物体放在旋转圆台上,它们与圆台之间的动摩擦因数均为μ,物体A的质量为m,物体B、C的质量均为2m,A、B离轴心距离为R,C离轴心距离为2R,当圆台旋转时下列说法中正确的是
( )
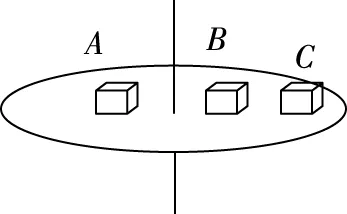
图1
A.在圆台匀速转动时,如果三个物体相对圆台都没有滑动,则物体C的向心加速度最大
B.在圆台匀速转动时,如果三个物体相对圆台都没有滑动,则物体B受到的摩擦力最大

D.当圆台转速增加时,三个物体发生滑动的先后顺序是C、B、A
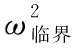
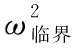
【变式1】如图2所示,两个质量分别为2m和m的小木块a和b(可视为质点)放在水平圆盘上,木块a与转轴OO′的距离为L,木块b与转轴OO′的距离为2L,a、b之间用长为L的强度足够大的轻绳相连,木块与圆盘的最大静摩擦力为木块所受重力的μ倍,重力加速度大小为g。若圆盘从静止开始绕转轴缓慢地加速转动,开始时轻绳刚好伸直但无张力,用ω表示圆盘转动的角速度,下列说法正确的是
( )
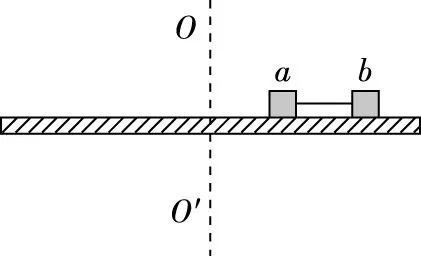
图2
A.物体a所受的摩擦力先达到最大静摩擦力
B.发生滑动前a的摩擦力一直增大,b的摩擦力先增大后不变
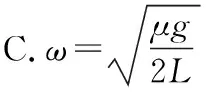
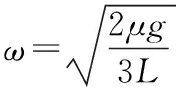
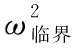
【点拨】虽然本题中两物体之间比例1中多了一根轻绳,在研究对象、受力分析、临界情形和临界值等方面有所不同,但实际是例1中知识的应用与延续,因为在绳绷紧之前的分析和结论与例1是完全相同的,物体滑动的先后顺序与质量无关、与半径有关;b受到的摩擦力达到最大静摩擦力之后轻绳会绷紧,作用在b上的拉力指向圆心且不断增大,用于补充b的向心力的增加,但作用在a上的拉力是背离圆心的,Ffa=FT+2mω2L,所以a的摩擦力会随角速度的增大继续增大,当二者摩擦力都达到最大静摩擦力之后a、b整体将远离圆心运动。
【变式2】如图3所示,用强度足够大的轻绳连接放在水平圆盘上的两个相同小木块a和b(均可视为质点),a与转轴OO′的距离为L,b与转轴OO′的距离为2L,小木块质量均为m,木块与圆盘间的动摩擦因数为μ,重力加速度大小为g。若圆盘从静止开始绕转轴缓慢地加速转动,则
( )
A.a与圆盘间的静摩擦力先达到最大静摩擦力
B.发生滑动前,a的摩擦力一直增大,b的摩擦力先增大后不变
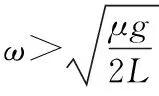
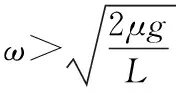

图3
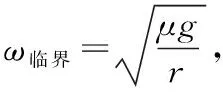
【点拨】本题也是例1中知识的应用与延续,虽然从外形来看与变式1十分相似,但摩擦力的变化规律却不同,原因是两木块在转轴的同侧和异侧的受力情况不同,当绳绷紧之后变式1中绳对a的拉力方向背离圆心,而变式2中绳对a的拉力方向是指向圆心的。因为受力情况不同,有可能出现不同质量比的变化规律和临界情形不同。在例1和变式1中木块之间的质量比不同不影响摩擦力的变化趋势和极值情境,即例1中木块滑动的先后顺序,变式1中木块b的摩擦力先达到最大后不变,a的摩擦力继续增大到最大静摩擦力之后,两木块将远离圆心运动等方面均与木块的质量没有关系;在变式2的模型中,绳绷紧之前,无论两物体间质量是怎样的关系,b木块的摩擦力总是先达到最大值,但是在绳绷紧之后,不同质量比有着不同的变化规律和临界情形。由向心力公式Fa向=maraω2,Fb向=mbrbω2可以看出随角速度的增大,两木块所需向心力的增加量间的大小关系与质量和半径的乘积有关,当mara
二、竖直面内非匀速圆周运动中的临界极值问题
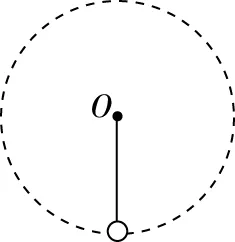
图4
【例2】如图4所示,一质量为m的小球用长度为L的细线悬挂于O点,已知细线能够承受的最大张力为7mg,重力加速度为g,在最低点给小球一个初速度,让小球在竖直平面内绕O点做完整的圆周运动,下列说法正确的是
( )
D.小球通过最高点的最小速度为零
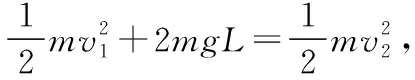
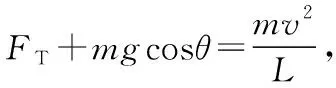
【变式】如图5所示,质量为M的支架(包含底座)上有一水平细轴,轴上套有一长为L的轻质细线,绳的另一端拴一质量为m(可视为质点)的小球。小球在竖直面内沿圆周运动时能经过最高点,忽略一切阻力,重力加速度为g。则
( )
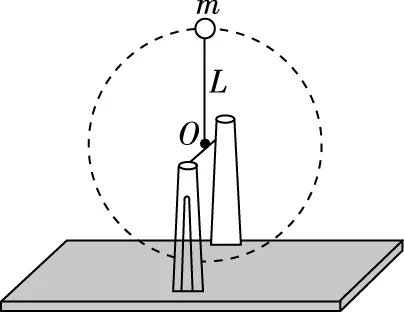
图5
A.如果支架始终保持静止,则小球运动到最低点时底座对地面压力最大
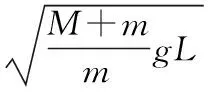
C.如果支架始终保持静止,则小球运动过程中地面对底座始终无摩擦力
D.如果支架始终保持静止,小球运动至右边与O点等高时,地面对底座的摩擦力向左