细品经典试题 体味正交分解奥妙

福建 姚龙楷

正交分解法作为物理中处理矢量问题的一种基本方法，本质上就是把表示矢量性的物理量放在平面直角坐标系中，沿坐标轴方向进行分解，将矢量的分量转化为代数量，进行代数运算。如果我们能在解决物理习题的过程中，灵活应用正交分解法，将复杂的解题过程及运算过程简化，一些问题便可迎刃而解。

一、合理建立直角坐标系，使解题更简便

【例1】物体A、B叠放在固定斜面上。A、B的质量分别为mA、mB，斜面倾角为θ，斜面与B之间的动摩擦因数为μ，B的上表面水平且不光滑(如图)。现用与斜面平行的力F推B，使A、B一起保持相对静止，沿斜面向上做加速运动。求A受到的支持力和摩擦力。

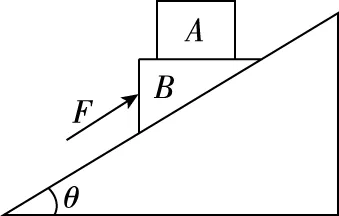
图1

【解析】由于A、B一起沿斜面向上做加速运动，可将A、B整体作为研究对象，先求出它们的共同加速度a，分析受力，并建立如图2所示直角坐标系。

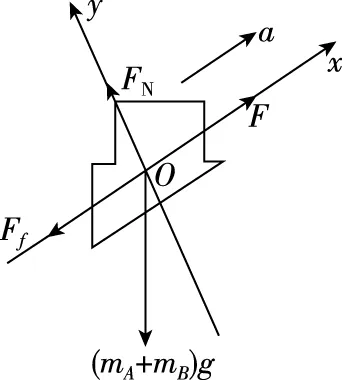
图2

受力分析有F-(mA+mB)gsinθ-Ff=(mA+mB)a

FN=(mA+mB)gcosθ

Ff=μFN

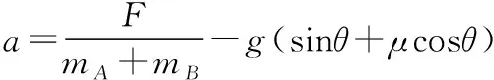
若要求出A受到的支持力和摩擦力，就以A物体为研究对象，分析受力后，如何建立坐标系呢?

一种方法是仍以a方向为x轴正方向，垂直斜面向上的方向为y轴正方向。这样，A受到的重力mAg、摩擦力Ff、支持力FN，都要分解。由于分解的力过多，会给解题带来不必要的麻烦。若以水平向右为x轴正方向，竖直向上为y轴正方向，这样，三个力都不需要分解，只要分解a即可。

如图3所示：ay=acosθ，ay=asinθ

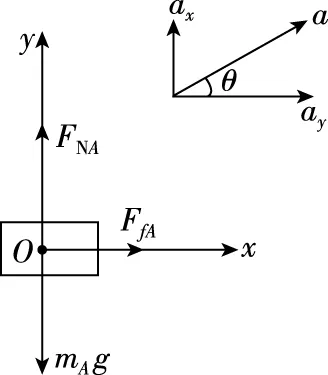
图3

根据坐标轴方向建立牛顿第二定律的方程，有

FNA-mAg=mAay

FfA=mAax

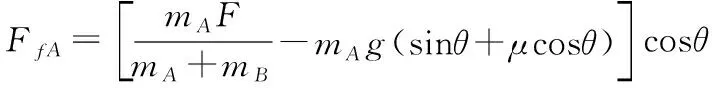
【点评】从理论上讲，使用正交分解时，直角坐标系的坐标轴方向的选定是任意的。但在处理具体问题时，选择较为合理的坐标轴方向，可使问题的解法简化。在建立坐标系时，让尽可能多的矢量与坐标轴在同一直线上，避免分解过多的矢量，使运算简便。

本题求加速度a时，是以加速度a的方向为坐标轴的正向。这样做的目的是在y轴方向上不出现a的分量，避免分解加速度，仅在x方向上列出牛顿第二定律的方程，而在y轴方向上只列出力平衡条件方程，简化了方程，简便了运算。在求A受到的FfA和FNA时，并不以a的方向为坐标轴正向，而以水平向右、竖直向上分别为x轴和y轴的正向，避免分解过多的力，仅分解加速度a，同样也是为了简化运算。可见要灵活地选择坐标轴方向，避免分解过多的矢量，有助于方便运算。

二、根据运动的实际效果，确定正交分解方向

【例2】如图4所示，在离水面高为H的岸边，有人以v0的匀速率收绳使船靠岸(假设绳子不可伸长)，当船与岸上的定滑轮水平距离为s时，船速大小是多少？

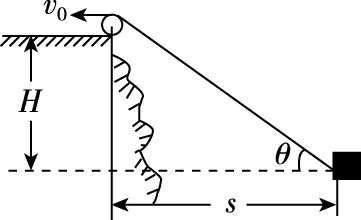
图4

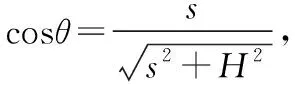
图5

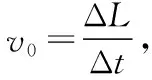
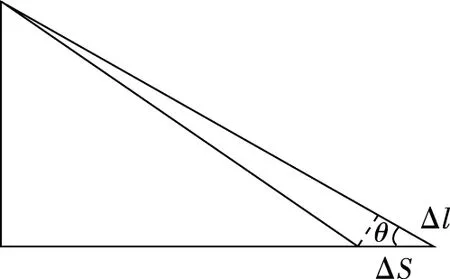
图6

(2)变式训练：如果船在靠岸过程中，水对船的水平阻力Ff大小不变，问在小船匀速靠岸的过程中，人对绳的拉力大小如何变化？(提示：把绳子拉力分解为水平和竖直两个分量，其中Fcosθ=Ff，绳的拉力不断增大。)

三、用正交分解法理清复杂的运动过程

【例3】如图7所示，在竖直平面内，一个带电量为-q的油滴，从O点以速度v射入方向水平向右的匀强电场中，v的方向与电场方向成θ角。已知油滴的质量为m，测得油滴到达运动轨迹的最高点时，它的速度大小又为v。求：

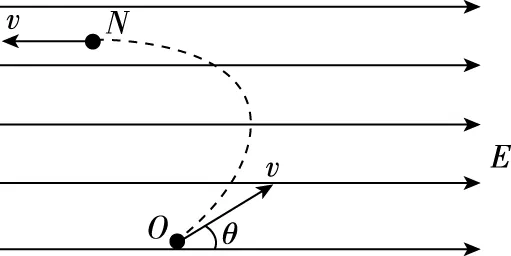
图7

(1)最高点的位置可能在O点上方的哪一侧？简要说明理由；

(2)最高点处(设为N)与O点的电势差U；

(3)电场强度E。

【解析】(1)对油滴受力分析可知，在竖直方向上受竖直向下的重力，在水平方向上受水平向左恒定的电场力。这就暗示我们可将油滴的运动按水平、竖直两个方向进行分解，油滴在水平方向上向右以初速度为vcosθ做匀减速直线运动，速度变为零后又向左做匀加速运动，在竖直方向上做初速度为vsinθ的竖直上抛运动，油滴到达最高点时竖直分速度变为零，此时只有水平分速度。当水平分运动中油滴回到出发点O的左方时，速度大小才可能等于v。所以最高点的位置只能在O点的左上方。

从O到N，由动能定理可知UNOq-mgh=0

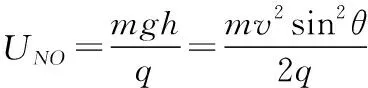
(3)从O点到N点过程中，竖直方向上vsinθ=gt

设水平方向油滴运动的加速度为a，则-v=vcosθ-at，Eq=ma

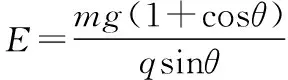
【点评】1.第(1)问也可用动能定理分析。由题意可知，油滴带负电荷，油滴运动到最高点过程中由于重力做负功，则电场力只能做正功，才能保证初态与末态的动能不变，所以最高点的位置只能在O点的左上方。第(3)问也可由动量定理求解，从O点到N点过程中，竖直方向有mgt=mvsinθ，水平方向有qEt=mv+mvcosθ，消去t可求E。

2.物体在某方向上的分运动形式只与该方向上的受力情况以及初始条件有关。我们将实际运动分解为两个分运动时，往往要根据受力方向来确定两个分运动的方向。这也是物理学中常提到的“力的作用与运动的独立性原理”。那么本题的解题思路会很自然地联想到“水平方向”和“竖直方向”两个正交方向，并运用相应规律来求解。

【例4】如图8所示，一个光滑的圆弧形槽半径为R，放在水平地面上，圆弧所对的圆心角小于5°。AD的长为x，今有一小球m1以沿AD方向的初速度v从A点开始运动，要使小球m1可以与固定在D点的小球m2相碰撞，那么小球m1的速度v应满足什么条件？

图8

【解析】把m1的运动分成两个分运动，其一是沿AD方向的匀速运动，因为在这个方向上m1不受力，其二是沿AB圆弧的运动，相当于摆长等于圆弧槽半径的单摆运动。而两个分运动具有等时性。

在AD方向上x=vt①

在AB弧上运动，等效成单摆运动t=nT②

【点评】在一些较为复杂的运动中，合运动的轨迹往往无法准确地描述出来，但正交方向上的分运动规律却很容易得出。利用分运动的规律，就可以求出结果，而不必寻找实际运动的准确轨迹。

四、回避矢量不确定性带来的影响

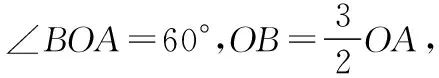
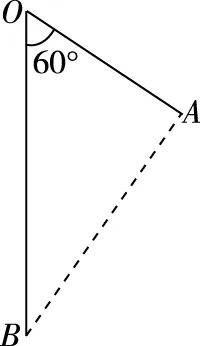
图9

(1)无电场时，小球到达A点时的动能与初动能的比值；

(2)电场强度的大小和方向。

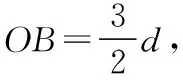
dsin60°=v0t①

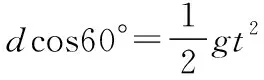
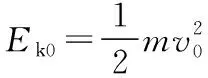
设小球到达A点时的动能为EkA，则

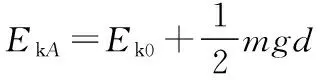
(2)加电场后，小球从O点到A点，其动能增加量比未加电场时多，可知电场力必做正功，电场有向下的分量。

设电场强度为E，将场强正交分解如图10所示，两分量分别为Ex、Ey。

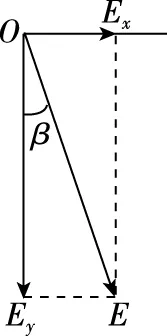
图10

未加电场时，对小球从O点到A点，由动能定理得

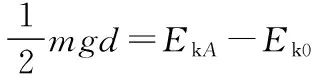
加电场时，对小球从O点到A点，由动能定理得

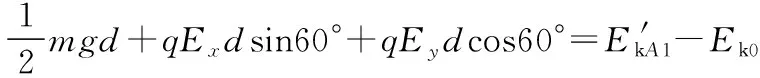
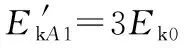
对小球从O点到B点，由动能定理得

其中EkB=6Ek0

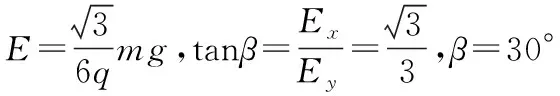
【点评】本题我们先把不确定的场强E分解成两个方向正交的分量，采用“先分后合”策略，结合正交分解法及动能定理解决这道难题。一般来说，用牛顿第二定律和运动学知识求解的问题，用动能定理也能求解，而且用动能定理求解更简捷。但是，由于本例题中小球运动的轨迹无法精确地描述出来，应用牛顿第二定律和运动学知识不一定能求解，应该优先考虑应用动能定理。

五、解决复杂的极值问题

【例6】如图11所示，长为L的细线拴一个质量为m的小球悬挂于O点，现将小球拉至与O点等高的位置且线恰被拉直。求放手后小球摆到O点正下方的过程中重力做功的最大功率。

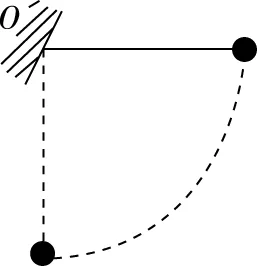
图11

【解析】重力做功功率P等于重力mg与小球的竖直分速度vy的乘积。可知要求重力做功的最大功率Pm的关键在于求vy的最大值。小球在水平位置由静止释放后，其运动速度在竖直方向的分量由零逐渐增大，然后又逐渐减小，到最低点时竖直分速度减小到零。设细线和水平方向夹角为θ时小球竖直分速度最大，因此，当竖直分加速度为零，即竖直方向合力为零时，小球竖直速度最大。即有

FTsinθ=mg①

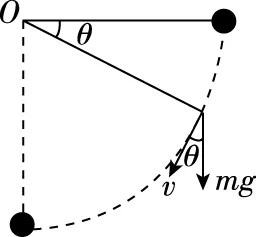
图12

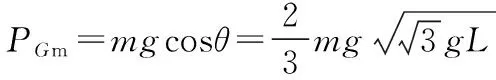
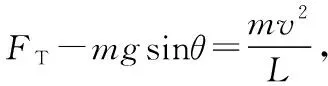
六、结束语