高考几何光学中的常见模型分析
2020-11-16甘肃张金龙田生杰
甘肃 张金龙 田生杰
光在玻璃砖中的折射和反射问题是高中物理光学部分的重点,也是高考考查的热点,题型多以计算题的形式出现。这部分内容的难点是将光学问题与数学知识结合,体现了物理核心素养中的模型构建、科学推理及科学论证,要求学生能够根据问题情景建立模型,运用全反射定律、折射定律和数学知识处理物理等问题。涉及的数学内容包括圆的知识、三角形知识、三角函数和正余弦定理等。
一、解题要点
1.求解光的折射、全反射问题的五点提醒
(1)光从一种介质斜射到另一种介质的分界面时同时发生折射和反射,如果光从光疏介质斜射入光密介质,则折射角小于入射角;如果光从光密介质斜射入光疏介质,则折射角大于入射角。
(2)光密介质和光疏介质是相对而言的。同一种介质,相对于其他不同的介质,可能是光密介质,也可能是光疏介质。
(3)如果光线是从光疏介质射入光密介质,则无论入射角多大,都不会发生全反射现象。
(4)折射现象中,光路是可逆的;光的反射和全反射现象,均遵循光的反射定律,光路均是可逆的。
(5)当光斜射到两种介质的界面上时,往往同时发生光的折射和反射现象,但在全反射现象中,只发生反射,不发生折射。
2.应用光的折射定律解题的一般思路
(1)根据入射角、折射角及反射角之间的关系,作出完整的光路图,注意入射角和折射角均以法线为标准。
(2)充分利用光路图中的几何关系,确定各角之间的关系,根据折射定律求解相关的物理量。
(3)注意在折射现象中,光路是可逆的。
3.解决全反射问题的一般步骤
(1)确定光是从光密介质射入光疏介质。
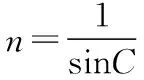
(3)根据题设条件,判断光在传播时是否发生全反射。
(4)如果发生全反射,画出入射角等于临界角时的临界光路图。
(5)运用几何关系、三角函数关系以及反射定律等进行分析、判断及运算来解决问题。
4.求解全反射现象中,光传播时间问题的注意事项

(2)全反射现象中,光的传播路程l应结合光路图和几何关系进行确定。

二、光的折射、全反射模型分析
模型一 平行玻璃砖模型
平行玻璃砖模型是指两个侧面相互平行的玻璃砖或同种均匀介质,光路特点及对光线的作用如图1所示,通过平行玻璃砖的光线不改变传播方向,但要发生侧移。
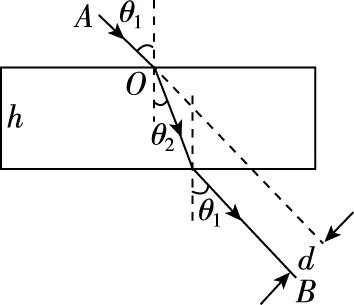
图1
【注意】(1)侧移距离的大小d与介质的折射率n、介质的厚度h及入射角θ1的大小等有关。
(2)根据光在折射过程中光路可逆,上述过程不可能发生全反射。
(3)应用本模型可以测定玻璃等介质的折射率。
【例1】如图2所示,AB、CD分别是置于空气中厚玻璃砖的上、下两个表面,且AB∥CD,光线经AB表面射向玻璃砖,当折射光线射到CD表面上时,下列说法中正确的是
( )
①不可能发生全反射 ②只要适当增大入射角θ1,就可能在CD面上发生全反射 ③只要玻璃砖足够厚,就可能在CD面上发生全反射 ④由于不知道玻璃的折射率,故无法判断是否能在CD面发生全反射

图2
A.① B.②③ C.②③④ D.④


图3
故折射光线O1O2在CD面上不能发生全反射,选项A正确。
【点评】本题考查光在平行玻璃砖中的传播问题,根据折射定律和反射定律正确作出光路图,再结合全反射的条件分析即可得出结果。当然本题也可直接利用模型一注意中第(2)条结论,光线通过平行玻璃砖的两个平行侧面过程中不可能发生全反射。
模型二 三角形玻璃砖模型
三角形玻璃砖模型(也称三棱镜)是指横截面为三角形的玻璃砖,其横截面可分为:一般三角形、直角三角形、等腰三角形、等边三角形等多种。光路特点及对光线的作用如图4所示,通过三棱镜的光线经两次折射后,出射光线向棱镜底边偏折。

图4
【注意】(1)调整入射角,光线在AC面的出射方向会改变,可能在AC面上发生全反射。
(2)两种特殊入射方向①光线平行于BC边入射;②光线垂直于AB边入射。两种情况光线在其他面上可能发生全反射。
(3)利用直角三角形或等腰三角形可制成全反射棱镜,改变光的传播方向。
【例2】如图5所示,直角三角形ABC为一棱镜的横截面,∠A=90°,∠B=30°。一束光平行于底边BC射到AB边上并进入棱镜,然后垂直于AC边射出。求:(1)棱镜的折射率;(2)保持AB边上的入射点不变,逐渐减小入射角,直到BC边上恰好有光射出,求此时AB边上入射角的正弦值。

图5
【解析】(1)光路图及相关量如图6所示。

图6

由几何关系和反射定律得β=β′=30°

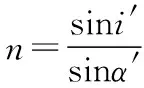
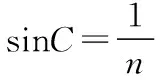
由几何关系得C=α′+30°
【点评】1.本题是一道典型的直角三角形棱镜模型问题,第一问根据光线沿平行三棱镜的一个面这个特殊的方向射入棱镜,求解折射率,第二问通过改变入射光的方向实现了在BC边恰好发生全反射的临界状态。
2.题目考查光的折射定律和全反射定律,正确解题的关键是能够准确作出光路图,注意入射角、折射角均以法线为标准。
3.根据几何关系寻找角度之间的关系,灵活运用数学公式sin(α-β)=sinαcosβ-cosαsinβ是快速求解的保证。
模型三 半球形(球形)或半圆形(圆形)玻璃砖模型
半圆形(球形)玻璃砖模型是指横截面为半圆形的玻璃砖,光路特点及对光线的作用如图7所示。
【注意】(1)光线沿球面斜射入,法线是过圆心的直线,经过两次折射后向圆心方向偏折,由圆的几何特性及光路可逆可知,光路不可能发生全反射现象,如图7所示。

图7
(2)光线沿半径方向从球面射入,光线必经过球心,在直径面上有可能发生全反射,如图8所示;

图8
(3)光线沿与半球形直径面垂直方向射入,由于入射点不同,在球面上可能发生全反射,法线为此点与球心的连线,如图9所示。
(4)如果入射光线过半球形直径面圆心,则折射光线必沿半球体半径方向出射,如图9所示。

图9


图10


图11
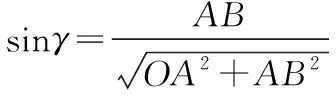
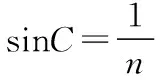
在玻璃体球面上光线恰好发生全反射时,光路图如图12所示。设此时光线入射点为E,折射光线射到玻璃体球面的D点。由题意可知∠EDO=C。

图12

【点评】1.本题是典型的半球体模型问题,考查光的折射定律和全反射定律,难度适中。
2.题目描述的情景是入射光线过半球形直径面圆心,同上文模型三中注意(4),折射光线必沿半球体半径方向出射的情况,当入射光线向左平移后,在半球面上发生全反射现象。
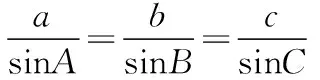
4.光线从半球体直径面射入时,法线与直径面垂直,光线射到半球体球面处时,法线过圆心沿半径方向。
模型四 圆柱体模型
如图13所示为圆柱体模型的横截面图,法线为过柱心的直线,如果光线垂直于圆柱体中心轴线沿半径方向射入,则光线通过柱心不改变传播方向;如图14所示,如果光线以其他入射角沿截面射入圆柱体,光线向靠近柱心方向偏折;如图15所示,如果光线垂直于圆柱体横截面(沿圆柱体中心轴线方向)射入,则沿直线继续传播;如图16所示,如果光线以其他角度射入圆柱体横截面,则在横截面处发生折射现象,在圆柱体内壁处可能发生全反射现象。
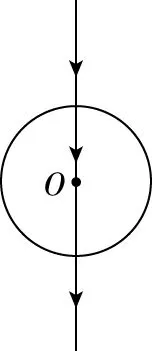
图13

图14

图16
【例4】如图17所示为一光导纤维(可简化为一长玻璃丝柱体)的示意图,玻璃丝长为L,折射率为n,AB代表端面。已知光在真空中的传播速度为c。求:(1)为使光线能从玻璃丝的AB端面传播到另一端面,求光线在端面AB上的入射角应满足的条件;(2)光线从玻璃丝的AB端面传播到另一端面所需的最长时间。

图17


图18

光速在玻璃丝轴线上的分量为vx=vsinα

【点评】1.本题是一道非常典型的光在均匀介质中传播的实际应用问题,属于圆柱体模型问题,考查光的折射定律、反射定律及全反射知识,考查应用数学知识处理物理问题的能力,难度适中。
2.解答本题须了解要使光线能够在玻璃丝中传播,光线在玻璃丝内壁处能够发生全反射,入射角应大于等于临界角。
模型五 其他不规则形状的模型
高考几何光学考题中不仅考查光在以上常见模型(介质均匀,形状规则)中的传播,还可能涉及其他模型(介质均匀,形状不规则)。无论什么形状的介质,光线传播都遵循光的反射定律和折射定律,正确作出光路图是解决问题的前提。
【例5】宝石因特殊的材质和独特的形状而闪闪发光,打磨某剖面如图19所示的宝石时,必须将OP、OQ边与轴线的夹角θ切割在θ1<θ<θ2的范围内,才能使从MN边垂直入射的光线在OP边和OQ边都发生全反射(仅考虑如图19所示的光线第一次射到OP边并反射到OQ边后射向MN边的情况),则下列判断正确的是
( )
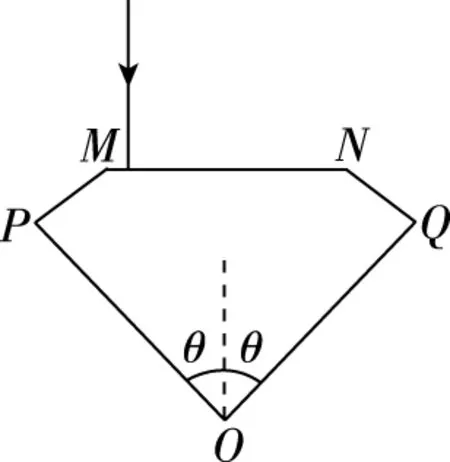
图19
A.若θ>θ2,光线一定在OP边发生全反射
B.若θ>θ2,光线会从OQ边射出
C.若θ1<45°<θ2且θ=45°,最终的出射光线将平行于入射光线
D.若θ<θ1,光线会在OP边发生全反射
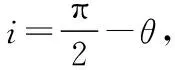

若θ1<45°<θ2且θ=45°,由几何关系可知光线在OP、OQ边会发生全反射,垂直MN射出,即出射光线将平行于入射光线,选项C正确。


模型六 涉及长度、面积等照射范围问题
涉及长度、面积等照射范围的光学问题在高考中经常会出现,解题关键是运用动态的思维方式思考,确定临界位置,在此基础上确定光的传播范围。
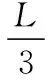
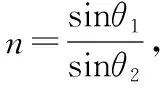

图21
【点评】1.本题第(2)问要确定在桌面上形成的光斑面积,属于确定照射范围类问题,难度适中。
2.光束沿中心轴射入玻璃圆锥表面,进入玻璃发生折射现象,正确作出光路图;确定边界光线是解决本题的关键所在。
3.注意结合对称性和几何知识分析求解。
三、总结

