基于“最近发展区”理论指导下的高中数学教学
——以“函数的概念”教学为例
2020-11-15安徽王东旭
安徽 王东旭
一、“最近发展区”理论概述
“最近发展区”理论是由前苏联著名心理学家维果斯基提出的,他认为学生的发展有两种水平:一种是现有发展水平,指独立活动时所能达到的解决问题的水平;另一种是潜在发展水平,是指学生通过学习能够获得的潜力.两者之间的差异就是“最近发展区”.教学应着眼于学生的“最近发展区”,在教学方法上应循序渐进,逐步向新知过度,不断超越其最近发展区而到达下一发展阶段的水平.
二、高一新生“函数的概念”的现有发展水平和潜在发展水平分析
本节课是针对刚刚步入高中大门的高一新生来设计的.高一新生在初中阶段已经初步学习了函数的概念以及几种特殊的函数:一次函数、反比例函数和二次函数,这些构成了学习本节内容的基础.然而他们在思维方式上往往还停留在具体运算,或者是基于一些具体问题的运算上.例如,他们看待函数时,一般习惯将其看作具体的一次函数、二次函数或者反比例函数,没有将其抽象看成一般的函数f(x).同时,在数学活动的经验上,大部分学生往往习惯于一些特殊值的运算,习惯通过特殊值代替抽象字母,将抽象的数学问题特殊化,从特殊的问题中推测、归纳出一般问题的答案.同时,通过初中三年的数学学习,大部分学生具备了一定的探究能力,掌握了一些合情推理和归纳总结的方法,但是这些能力和方法普遍都是建立在具体问题或者几何直观基础上的,学生并不懂得如何借助抽象的数学符号进行.鉴于以上对学生现有发展水平的分析,教师在回顾旧知的基础上提出一系列概念判断性的问题,其中有些问题学生无法利用初中函数的概念解释,亦无法借助特殊化的方式判断.因而需要明确本节课学习的目的——从集合的角度重新解读函数的概念.
三、《普通高中数学课程标准》(2017年版)对函数的概念教学的要求
《课程标准》对本节的教学要求是:通过丰富实例,进一步体会函数是描述变量之间的依赖关系的重要数学模型,在此基础上学习用集合与对应的语言来刻画函数,体会对应关系在刻画函数的概念中的作用,了解构成函数的要素.从学生已掌握的具体函数和函数的描述性定义入手,引导学生联系自己的生活经历和实际问题,尝试列举各种各样的函数,构建函数的一般概念.然而函数的概念本身是极其抽象的,要求学生用变量的眼光、运动变化的观点去看待问题,这点对于高一新生来说学起来十分不易.在数学的教学中,要求教师强调函数本质,淡化函数形式化表示与运算.通过具体实例提炼函数的概念的本质,使学生真正理解它、运用它.
四、“最近发展区”理论指导下的函数的概念教学设计
“最近发展区”是重要的教学理论,为了能够清楚的表达该理论在本节教学中的指导作用,笔者将教学主要分成以下5个环节:回顾旧知、创设情境、引发冲突、形成新知、深化理解.具体如下:
1.回顾旧知
师:初中学过哪些函数?到底什么叫做函数?
【设计意图】通过让学生回忆学习过的几种特殊函数:一次函数、二次函数和反比例函数,从而引导学生回忆起初中课本里的函数的概念以及初中解决此类问题时的惯用方法和思路.在教学的伊始就唤醒并构建起学生函数的概念学习的现有发展水平中的知识内容.
生:回忆并思考上述问题,并让学生简答.
师:给出初中时对函数的概念的描述:“一般地,设在一个变化过程中有两个变量x和y,如果对x在它允许取值范围内的每一个值,y都有唯一的值与它对应,那么就说x是自变量,y是x的函数.”
2.创设情境
通过生活中现实问题、熟悉的实例来创设教学情境,这样容易引起学生产生共鸣、产生兴趣,体现“人人学有用的数学”.
笔者给出以下几个具体实例,并进一步设问:以下变量关系是函数吗?为什么?
实例1.下表是1950~1959年我国的人口的数据资料:人口数量单位(万人)

年份(x)1950195119521953195419551956195719581959人数(y)55 19656 30057 48258 79660 26661 45662 82864 56365 99467 207
实例2.如图是滁州市2019年某天自零点至24点气温变化情况.
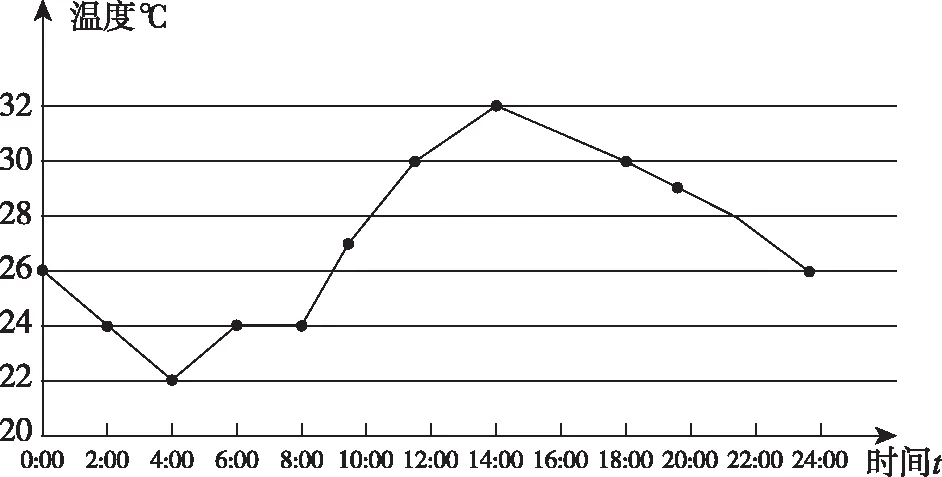
实例3.某趟高铁列车以300 km/h的时速匀速行驶,行驶的路程y千米与其行驶时间x小时之间的关系.
实例4.已知y=x2,变量y与变量x之间的关系.
实例5.已知y2=x(x为非负实数),变量y与变量x之间的关系.
实例6.已知|y|=x,变量y与变量x之间的关系.
【设计意图】由于这几个实例是完全建立在学生的现有发展水平的基础之上的,所以应该由学生独立思考完成,教师此时不应该给予提示和指导.根据学生现有的水平,容易判断出实例1,2,3,4中,y是x(或t)的函数;而实例5,6中,y不是x的函数.
3.引发冲突
提出疑问:既然初中已经学习过函数的概念,为何高中又要学习函数的概念?
【设计意图】这样的设问方式正是学生所感到困惑的地方,因此可以吸引学生的注意,有效地激发学生的学习兴趣和学习动机.
笔者紧接着给出下列式子并提出问题:这些式子是函数吗?
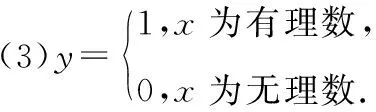
【设计意图】通过初中阶段的学习,学生会习惯性地把函数理解为“一个变量随着另一个变量变化而变化”,对于以上的这类式子是否表示函数,绝大多数的高一学生无从判断,因为这与初中“变量说”的定义不太吻合,于是学生感到疑惑.这时,要让学生知道“变量说”仅从运动变化的观点出发,强调的是两个变量和变域——自变量与因变量、定义域与值域,缺少了对于函数实质的刻画.因此需要从新的角度来引入函数更为准确的定义.在课堂教学时可以通过这些函数的实例,在学生的现有发展水平的基础上引发学生的认知冲突,促使学生积极自主探索,促进学生从现有发展水平出发,最终完成向潜力发展水平的过渡和转化.
4.形成新知
教师带着学生回到之前给出的几组实例,引导学生用集合的语言阐述实例1,2,3,4的共同特点.
(1)每一个变化过程均涉及两个非空数集A,B;
(2)存在某种对应法则,对于A中的任意元素x,B中总有唯一确定的一个元素y与之对应.
在此,笔者通过PPT展示实例1可以确定的两个非空数集:
以年份构成的集合A={1950,1951,1952,1953,1954,1955,1956,1957,1958,1959},
以人口数量(万人)构成的集合B={55 196,56 300,57 482,58 796,60 266,61 456,62 828,64 563,65 994,67 207}.并给出这两个非空数集之间的对应,这种对应是每一个年份都对应着一个人口数量.
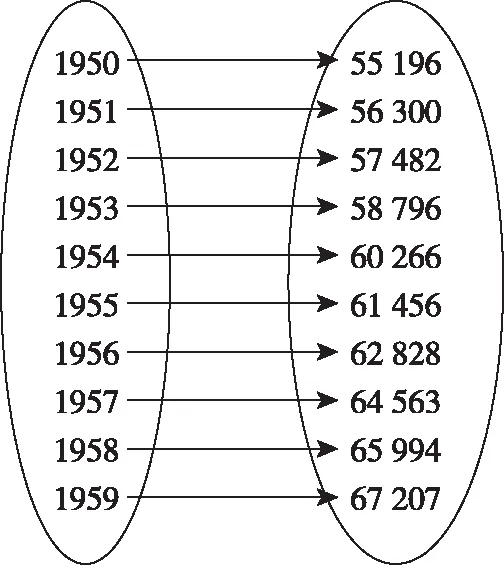
于是,引导学生模仿实例1中两个数集之间的对应,完成实例2的对应.并以投影的形式在班级展示.这里采集一位同学的答案:
实例2.A={0:00,2:00,4:00,6:00,8:00,10:00,12:00,14:00,16:00,18:00,20:00,22:00,24:00},
B={20,21,22,23,24,25,26,27,28,29,30,31,32}.

再让学生口述实例3,4如何用集合之间的对应来描述.在此基础上笔者给出函数的概念的定义:“一般地,设A,B是两个非空的数集,如果按某种对应法则f,对于集合A中的任意元素x,在集合B中都有唯一的元素y和它对应,那么这样的对应叫做从A到B的一个函数,通常记为y=f(x),x∈A.其中,所有的输入值x组成的集合A叫做函数y=f(x)的定义域;所有的输出值y组成的集合C(C⊆B)叫做函数y=f(x)的值域.”
【强化概念】由于学生初次碰到这个新概念,所以极容易忽略其中的一些关键部分,而对于这些关键部分认识上的缺失会直接导致其在后面学习上产生障碍.于是,在给出概念之后应当及时地强调函数的概念成立的几个必备条件:两个集合要求“非空”、两个集合必须是“数集”、“任意”和“唯一”.它们都是形成概念的必要前提,并且能够与本章最后要讲的映射的概念之间形成对比和联系.而对于其中“任意”和“唯一”这两点的充分理解是对学生现有思维方式的挑战.例如,学生应当理解“任意”是用来规定集合A的,于是集合A一定是函数的定义域,而其对于集合B却没有限制,集合B中可以有元素没有原象,于是集合B就不一定是值域,值域C一般包含于B,而不一定相等.如果学生能够对这两点达到正确的理解和熟练的运用,那么则是其从现有发展水平过渡到潜力发展水平的一个重要标志.
最后,回到刚才给出的三个式子.根据概括出的函数的概念,学生容易判断它们都是函数,这是一个已经转化为学生潜在发展水平的问题.在展现函数表现形式多样的同时,通过“特殊→一般→特殊”的认知循环发展过程,加深学生对于函数的概念的理解.
5.深化理解
学了新的函数的概念后,函数具体有哪些部分,这是学生必须搞清楚的,于是在前面引导的前提下继续追问.(让学生回答并点评)
由定义域、值域及定义域到值域的对应法则三部分组成,这就是函数的三要素,为了研究方便,我们把三要素写成一个表达式y=f(x).
“y=f(x)”表明,对于定义域中的任意x,在对应法则f的作用下都可得到y,可见对应法则孕育了x与y之间的关系,它是联系x与y的纽带,从而说明对应是函数的核心.
为了深化学生对概念中“对应”的理解,进一步提出问题:实例3和实例4所表示的函数y=300x(x≥0)与y=x2(x∈R)中对应法则分别表示什么呢?(学生作答,教师指导)


函数三要素的分析与研究是本课的重点和难点.这里将对y=f(x)的认识与f作用的分析作为学生理解函数三要素的最近发展区,使学生在突破重难点的基础上对f作为函数实质特征第一次认同.
上述的y=300x与y=x2显然不同,原因是二者的对应法则不同.那么,如何判定两函数是相等的函数呢,判定标准是什么?
笔者通过下面这个例子来讲,提出设问:下列函数中哪个与函数y=x相等?(让学生就这个问题展开讨论,然后找部分学生提出自己的想法)

追问:f(x)=x与g(t)=t,那么它们还是同一函数吗?(由学生作答)
于是可以得出结论:判断函数是否相同,只要看它们的三要素是否相同,而值域完全由定义域和对应法则来确定,所以主要是看定义域和对应法则是否相同.定义域和对应法则一经确定,则函数就完全确定了,与表示自变量的字母无关.而判断两函数不同,只需要判定定义域、对应法则和值域中有一个要素不同就可以了.
五、“最近发展区”理论在本节使用的反思
1.基于学生现有发展水平的教学设计
首先通过实例创设问题情境,提问学生初中关于函数的定义以及利用初中函数定义判断实例是否为函数,激起学生对已有知识的回忆与联想,同时也感受到初中定义的局限性,激发学生学习新知的愿望.引导学生用“初中x在某一确定范围内去理解非空集合A”,“初中某一变化过程去理解按照一定对应法则f”,这样处理有利于形成知识的正迁移.通过学生的“观察分析→比较→归纳→概括”培养学生抽象思维的能力,同时也培养了学生的创新意识.
2.基于学生潜在发展水平的引导
本节课的设置,让学生一开始就从现有发展水平出发,引发认知上的矛盾与冲突,从而促进学生积极自主地探索与反省,并让学生处于教师所激发形成的“思维场”中,在教师所创设的符合学生思维水平的一个个“最近发展区”内,让学生在解决冲突的过程中逐步完善自己的知识结构,提升自己的思维水平和基本数学能力,在“最近发展区”内,真正有效地把学生的现有发展水平转化为“潜在发展水平”,从而实现自身真正的发展.
