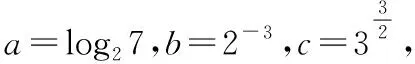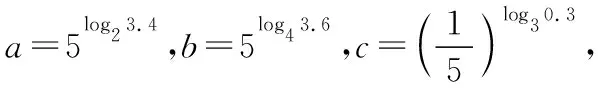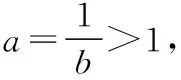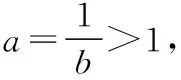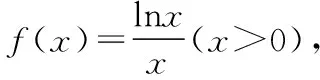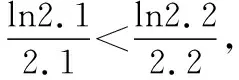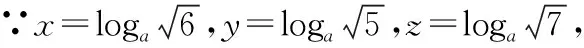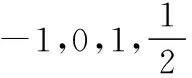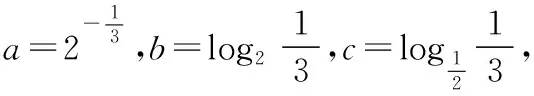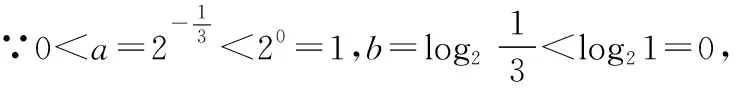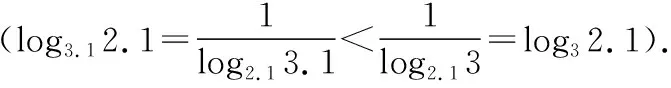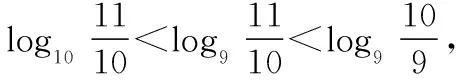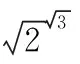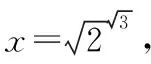心有“0”犀“1”点通
——浅议指对幂比较大小的常用技巧
2020-11-15四川杜海洋
四川 杜海洋
(作者单位:四川省成都经济技术开发区实验中学校)
从近几年高考情况来看,指数、对数及幂的大小比较为高考的热点内容,一般以选择题为主.这类考试题目通常是三个指数和对数及幂混在一起,进行排序.解决这类问题如果两两进行比较,有时则花费的时间较多,本文介绍处理此类问题的常用方法与技巧.
涉及指对幂比较大小时,如果式子中易求大于0或小于0先区分还容易办到,但让学生感到困难的是当式子的值都大于1或小于1时,此时的技巧手段就需要有高招了,即0,1是这类问题的分水岭,下面笔者以一些典型例题来说明此类问题的方法与技巧,以飨读者!
一、比较大小的基本思路
(1)求同存异:如果两个指数(或对数)的底数相同,则可通过指数(真数)的大小与指数(或对数)函数的单调性判断出指数(或对数)的关系,所以要熟练运用公式,尽量将比较的对象转化为某一部分相同的情况.
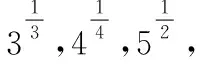
(2)利用特殊值作“中间量”:在指对数中通常可优先选择“-1,0,1”对所比较的数进行划分,然后再进行比较,有时可以简化比较的步骤(在兵法上可称为“分割包围,各个击破”),也有一些题目需要选择特殊的常数对所比较的数的值进行估计,例如log23,可知1=log22 (3)利用函数的单调性比较大小:例:f(x)在[a,b]上单调递增,则∀x1,x2∈[a,b],x1 总之,比较数式的大小,若同底,考虑指数函数(或对数函数);若同指,则考虑幂函数,再利用函数的单调性比较大小;若不同底,也不同指,则其基本方法是“同底法”,即把不同底的对数式化为同底的对数式,然后根据单调性来解决,或者利用中间量法. 策略一、估算法 就是把复杂问题转化为较简单的问题,求出答案的近似值,或把有关数值扩大或缩小,从而对运算结果确定出一个范围或作出一个估计,进而作出判断的方法. 【例1】比较log39.1与log23.9的大小. 【解析】因为1=log22 策略二、特殊值法 就是运用满足题设条件的某些特殊数值对各选择支进行检验或推理,利用问题在某一特殊情况下不真,则它在一般情况下也不真的原理,由此判断选项真伪的方法.用特例法解选择题时,特例取的越简单、越特殊越好. 【例2】若a>b>1,0 ( ) A.ac C.alogbc 【针对训练2】若非零实数a,b满足2a=3b,则下列式子一定正确的是 ( ) A.b>aB.b C.|b|<|a| D.|b|>|a| 【解析】令a=2,则4=3b,易得1 策略三、数形结合法 就是利用函数图象或数学结果的几何意义,将比较大小与某些函数图象结合起来,利用函数图象性质,再辅以简单计算,确定正确答案的方法. ( ) A.a>b>cB.b>a>c C.a>c>bD.c>a>b 在同一平面直角坐标系中分别作出函数y=log2x,y=log3x,y=log4x的图象,如图所示: ( ) A.x3 C.x1 策略四、单调性比较法 解题时根据实际情况来构造相应的函数,利用函数单调性进行比较大小,如果指数相同,而底数不同则构造幂函数,若底数相同而指数不同则构造指数函数.然后根据函数的单调性进行比较大小. 【例4】已知a=2.12.2,b=2.22.1,c=log2.22.1,则 ( ) A.c C.a 所以c ( ) A.x>y>zB.z>y>x C.y>x>zD.z>x>y 策略五、中间量法 【例5】 类型1、指数型(桥梁a0=b0=1) (1)比较大小1.70.3________0.93.1. 【解析】观察题目可发现两个数的底数、指数都不同,但可以根据指数函数的单调性,构造中间量,与数1先进行比较.知1.70.3>1.70=1=0.90>0.93.1. 注意:在研究指数函数时,总会提到a0=1(a>0,a≠1),即指数函数过定点(0,1),更深入一些理解,这个定点也是一个重要的分界点,把函数值分为了大于1和小于1两部分. 【解析】底数、指数都不同,构造中间量比较大小,先与数1,0比较. (3)已知a=log20.2,b=20.2,c=0.20.3,则 ( ) A.a C.c 【解析】a=log20.2 类型2、对数型(0=loga1=logb1),(1=logaa=logbb) ( ) A.a>b>cB.a>c>b C.c>a>bD.c>b>a (2)设a=log54,b=(log53)2,c=log45,则 ( ) A.a C.a 【解析】∵a=log54 ∴c最大,又因为a,b∈(0,1),但b=(log53) 【点评】本题考查指数的运算性质和对数的运算性质,在涉及比较两个数的大小关系时,有时借助于0,1这样的特殊值能起到事半功倍的效果. 类型3、以上讲的两种类型,都是用比较常见的0,1作为桥梁进行大小比较,然而有些值不能用0,1来作为中间量进行比较,但是我们仍然能够找到其他的中间量. 两者均大于1或均小于1且大于0 (1)0.80.5________0.90.4. 【解析】由式子可得两者均小于1,这时我们可以构造中间量0.90.5或0.80.4,目的是转化与其中一个式子构造同底,与另一个式子构成同指,即比较sm,tn的大小,构造中间量sn或tm.0.80.5<0.90.5<0.90.4. (2)log3.12________log32.1. (3)已知a=log910,b=log1011,比较a,b的大小. 【针对训练5】试比较log54与log43的大小. 即:比较logab,logmn的大小,构造中间量logan或logmb. 策略六、对数法比较大小 上面的题目可以用函数方法或中间量的方法来比较大小,但是有些题目,靠上述手段很难比较大小,我们就需要新的武器——对数法比大小.我们看下面的题目,这时就显示出对数法比大小的优势. 注意:此时中间量并不能判断出两数大小,所以我们转换思路,用取对数的方法,进行比较. 【针对训练6】若a>0,b>0,比较algb与blga的大小. 【点评】1.对数法比大小,先取对数,比较对数值的大小,得到真数的大小;2.只适用于比较两个正数的大小,遇到负数需要先做出转化. 指数、对数及幂的大小比较问题方法灵活,常常给人以“乱花渐欲迷人眼”的感觉,而对其问题进行归纳总结,会发现这类问题的解法往往可以从代数和几何两个方面加以探寻,即利用函数的性质及图象解答,体现对数学抽象、逻辑推理、数学建模、数学运算及直观想象等核心素养的考查.当然除了以上介绍的方法外还有作商、作差等比较大小的方法,有时一题也可从不同的方法入手均可获得突破,以上举例起到一个抛砖引玉的作用,平时在学习时多留意,多积累,相信以后解决此类问题时就会有“浅草才能没马蹄”的轻盈之感.二、比较大小的常用方法