训练深层抽象思维,培养核心数学能力
2020-11-15甘肃张建文
甘肃 张建文
数学抽象是数学核心素养的重要组成部分,是考查学生数学能力的主要指标.数学抽象是指通过对数量关系和空间形式的抽象,得到数学研究对象的素养.数学抽象的主要表现为:获得数学概念和规则,提出数学命题和模型,形成数学方法与思想,认识数学结构与体系.
1.数学抽象按照抽象的深度可以分为浅层次抽象和深层次抽象
浅层次抽象是深层次抽象的基础,只有经历了浅层次抽象才可以形成深层次抽象,深层次抽象是浅层次抽象发展的必然结果.
1.1浅层次抽象
在具体的实际情境中借助于若干具体的数学原型与实例,通过归纳类比的推理模式得到相关的数学概念或命题.浅层次数学抽象大多在新授课中进行,多在概念教学或命题教学中得到体现.
1.2深层次抽象
规则意识凸显,结构意图明了,主要在具体的数学情境中,通过对数学概念和命题的比较分析,得到结构更简单、表达式更简洁、应用更广泛的结论.深层次抽象主要体现在规则和结构这两个方面,即几何作图方面的规则性和操作性以及代数表达方面的简洁性和结构性.
2.数学抽象是可以通过系统训练得到发展与提高的,数学抽象思维的训练具有以下三重境界
2.1由特殊到一般的归纳式训练
这是数学抽象的正面训练模式,是最常见、最普遍的训练方法,也是形成浅层次数学抽象能力的主要渠道.归纳式训练分为完全归纳和不完全归纳两种,主要是以不完全归纳为主.通过分析大量实例,从数量与数量关系、图形与图形关系以及事物的实际背景中得到一般性的结论.教师主要创设一定的教学情境,引导学生探究讨论,最终师生达成共识得到结论.
2.2由一般到特殊的演绎式训练
这是数学抽象的反馈训练模式,即利用正面得到的结论去识别或分析具体数学对象.因为通过归纳式得到的一般性的结论具有一定的抽象性,自己建立起来的抽象思维是否正确、思维过程是否科学、结论是否牢固还有待检验,所以进行演绎式训练是对归纳式训练的有效补充和强化.
2.3透过现象看本质的拔高式训练
拔高式训练主要是对规则和结构的升级训练,是对数学对象的高层次认识,是提高学生创新能力的充分条件.数学抽象结论升华为一定的生活哲理,训练过程融入自己的情感与感受,是发展学生学习兴趣和强化学习动力的主要方式.
2.3.1规则训练:主要体现在几何作图上,目标是从抽象表达式中读懂对应图形的结构特点或操作方法,不同的抽象表达式当中蕴藏着不同的图形操作步骤和方法.根据抽象表达式确定图形的所有可能情形以及不同的变换方法之间的优劣.
2.3.2结构训练:主要体现在代数表达式上,通过比较研究抽象表达式结构上的相似性与差异性,求解或构造新的表达式来解决实际问题.如函数解答中的构造函数问题就是最具代表性的结构训练,这需要学生具备扎实的基础知识,能对问题有高屋建瓴的把握.
规则性与结构性是深度抽象的两个重要方面,两者相辅相成、相互转化,共同促进学生抽象思维能力的发展.
3.抽象表达式是训练学生高级思维的主要载体,下面通过对曲线对称性的研究,在规则和结构方面蕴含的特点进行简要分类说明.
3.1曲线关于点的对称
这里的曲线可以是函数图象,也可以是一般曲线,如椭圆、双曲线及抛物线等.
曲线f(x,y)=0关于定点M(a,b)的对称曲线方程为f(2a-x,2b-y)=0.
特别地,曲线f(x,y)=0关于原点O(0,0)的对称曲线方程为f(-x,-y)=0.
函数y=f(x)关于定点M(a,b)的对称函数为y=2b-f(2a-x).函数y=f(x)关于原点O(0,0)的对称函数为y=-f(-x).
3.2曲线关于线的对称
曲线关于直线的对称结果仍然是曲线,根据已知曲线和对称直线(对称轴)就可以求出新曲线的方程.
3.2.1曲线f(x,y)=0关于x轴的对称曲线方程为f(x,-y)=0;
3.2.2曲线f(x,y)=0关于y轴的对称曲线方程为f(-x,y)=0;
3.2.3曲线f(x,y)=0关于直线y=x的对称曲线方程为f(y,x)=0;
3.2.4曲线f(x,y)=0关于直线y=-x的对称曲线方程为f(-y,-x)=0;
3.2.5曲线f(x,y)=0关于直线x=a的对称曲线方程为f(2a-x,y)=0;
3.2.6曲线f(x,y)=0关于直线y=b的对称曲线方程为f(x,2b-y)=0.
由此可以抽象得到一般的曲线C关于直线对称的求解方法,即已知曲线C:f(x,y)=0,直线l:ax+by+c=0,下面可求曲线C关于直线l的对称曲线.
设P(x0,y0)为曲线C上的点,即f(x0,y0)=0.P关于直线l的对称点为Q(x,y),则有

特别地,函数y=f(x)关于定直线x=a的对称函数为y=f(2a-x).函数y=f(x)关于y轴的对称函数为y=f(-x).
3.3函数图象自身的对称性
函数图象具有某种对称性是函数自身的性质,而且是只有某一类特殊函数图象才具有的性质,比如奇函数与偶函数.而曲线关于点或线的对称是一种图象变换方式,这两者是有显著区别的.下面对函数y=f(x)的对称性进行简单论述.
3.3.1若函数y=f(x)满足:f(x)+f(2a-x)=2b,则y=f(x)关于点M(a,b)对称.
特别地,当函数y=f(x)满足:f(x)+f(-x)=0时,则y=f(x)图象关于原点对称,即y=f(x)是奇函数.
3.3.2若函数y=f(x)满足:f(x)=f(2a-x),则y=f(x)关于直线x=a对称.
特别地,当函数y=f(x)满足:f(x)=f(-x)时,则y=f(x)图象关于y轴对称,即y=f(x)是偶函数.
3.3.3抽象函数中的奇偶性:
若函数y=f(x+a)为奇函数,即f(x+a)+f(-x+a)=0,则y=f(x)关于M(a,0)对称.
若函数y=f(x+a)为偶函数,即f(x+a)=f(-x+a),则y=f(x)关于直线x=a对称.
3.4函数的奇偶性+周期性⟹对称性
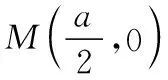
证明:由于y=f(x)为奇函数,所以f(x)=-f(-x).且f(x)=f(x+a),
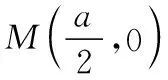

3.5函数的奇偶性+对称性⟹周期性
3.5.1若函数y=f(x)为奇函数,且关于点M(a,0)对称,则y=f(x)为周期函数,且周期T=2|a|(证明如下).
证明:由于y=f(x)为奇函数,所以f(x)=-f(-x).又由于函数关于点M(a,0)对称,所以有f(2a+x)+f(-x)=0,因此可得f(2a+x)-f(x)=0,即f(2a+x)=f(x).故y=f(x)为周期函数,且周期T=2|a|.
3.5.2若函数y=f(x)为奇函数,且关于直线x=a对称,则y=f(x)为周期函数,且周期T=4|a|(证明方法类似3.5.1,证明过程略).
3.5.3若函数y=f(x)为偶函数,且关于点M(a,0)(其中a>0)对称,则y=f(x)为周期函数,且周期T=4|a|(证明方法类似3.5.1,证明过程略).
3.5.4若函数y=f(x)为偶函数,且关于直线x=a对称,则y=f(x)为周期函数,且周期T=2|a|(证明方法类似3.5.1,证明过程略).
4.训练学生高级抽象思维的另一种主要手段是进行构造法训练.通过对抽象函数表达式结构的分析理解,构造恰到好处的新函数解决问题.
4.1根据任意函数构造对称函数

证明:由于F(x)=f(x)+f(a-x),所以F(a-x)=f(a-x)+f(x)

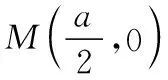
4.2根据任意函数构造分段对称函数
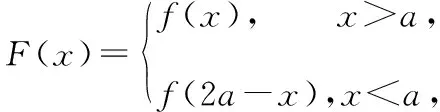
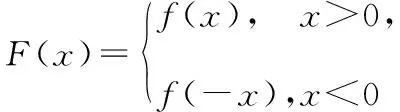

4.3根据导数具体形式构造函数

4.3.2已知y=f(x)满足:xf′(x)+f(x)<0,则可构造F(x)=xf(x).
构造法的应用在不同的实例当中有不同的表现形式,具体问题具体分析,不可一概而论.
5.典例赏析
5.1关于线的对称应用
【例1】(2015·全国卷Ⅰ·文12)设函数y=f(x)的图象与y=2x+a的图象关于直线y=-x对称,且f(-2)+f(-4)=1,则a=
( )
A.-1 B.1
C.2 D.4
【分析】此题明显属于曲线关于直线对称类问题,已知曲线C1:y=2x+a,曲线C1关于直线y=-x的对称曲线是C2:-x=2-y+a,即y=-log2(-x)+a,可得f(x)=-log2(-x)+a,
代入式子f(-2)+f(-4)=1,可得a=2.

( )
A.0 B.m
C.2mD.4m

【小结】例1需要求出对称曲线的方程,是两条曲线关于直线的对称问题,例2则要从抽象表达式中读出曲线的对称轴,是函数图象自身具有对称性.此两例堪称是关于直线对称的典范,其中包含的解答思路与方法具有很强的扩展性和普遍性.
5.2关于点的对称应用

( )
A.0 B.mC.2mD.4mm


【小结】此例是关于点对称模型的经典应用,和例2非常类似,都属于函数本身具有的对称性质.
5.3对称性与奇偶性的结合
【例4】(2018·全国卷Ⅱ·文12)已知f(x)是定义域为(-∞,+∞)的奇函数,满足f(1-x)=f(1+x).若f(1)=2,则f(1)+f(2)+f(3)+…+f(50)=
( )
A.-50 B.0
C.2 D.50
【分析】因为y=f(x)为奇函数,且图象关于直线x=1对称,所以f(x)的周期T=4.又由于f(0)=0,f(1)=2,f(2)=f(1+1)=0,f(3)=f(-1)=-f(1)=-2,f(4)=0,
所以f(1)+f(2)+f(3)+…+f(50)=12(f(1)+f(2)+f(3)+f(4))+f(1)+f(2)=2.
【小结】此题的解答关键在于根据已知条件得到f(x)的周期T=4,之后的求值计算就会迎刃而解,所以在理解与计算过程中要抓主抓重.
5.4构造对称函数
【例5】(2017·全国卷Ⅰ·文9)已知函数f(x)=lnx+ln(2-x),则
( )
A.f(x)在(0,2)单调递增
B.f(x)在(0,2)单调递减
C.f(x)的图象关于直线x=1对称
D.f(x)的图象关于点(1,0)对称
【分析】根据任意函数构造对称函数的方式可得,f(x)的图象关于直线x=1对称.
5.5导数中的构造法
【例6】(2015·全国卷Ⅱ·理12)设函数f′(x)是奇函数f(x)(x∈R)的导函数,f(-1)=0,当x>0时,xf′(x)-f(x)<0,则使得f(x)>0成立的x的取值范围是
( )
A.(-∞,-1)∪(0,1) B.(-1,0)∪(1,+∞)
C.(-∞,-1)∪(-1,0) D.(0,1)∪(1,+∞)


【小结】抽象函数的构造源于对式子的精准理解和独到把握,更需要提升深层抽象能力,从相似元素中找差异,从不同元素中找共性.
6.总结与展望
以上是笔者对数学抽象素养的一个侧面进行的论述,论述主要是以抽象函数的对称性为研究对象展开的,对抽象函数的对称性进行了多层次多角度的简单论述,希望对培养学生的抽象思维能有所帮助.在新课改的大潮流下,深入理解学生、理解教学都需要我们从全新的视角思考问题,做到因材施教、顺势而为,运用各种方式提高教与学的效率.
