试谈一道高考题中直观想象素养各水平的体现

湖北 周 威

《普通高中数学课程标准(2017年版)》(以下简称“课标”)对直观想象核心素养的内涵和主要表现做了具体描述，并将其划分为“三个水平”.如何理解具体试题中数学核心素养的应用与渗透？根据课标要求，在高考命题路径中对于每道试题，除了给出传统评分标准外，还需要给出反映相关数学学科核心素养的水平划分依据.本文基于直观想象素养的“水平划分”层次，探讨2019年全国卷Ⅲ理科数学21题中直观想象素养的水平层次和表现形式.

一、直观想象素养的内涵与水平划分

1.直观想象素养的内涵

课标明确提出，直观想象是指借助几何直观和空间想象感知事物的形态与变化，利用空间形式特别是图形，理解和解决数学问题的素养.主要包括：借助空间形式认识事物的位置关系、形态变化与运动规律；利用图形描述、分析数学问题；建立形与数的联系，构建数学问题的直观模型，探索解决问题的思路.直观想象是要依靠平面几何或空间几何的直观描述、理解和解决问题，提升学生的数形结合能力，在具体的情境中感悟事物的本质.

2.对直观想象素养的水平划分与理解

各个水平的含义描述分别从情境与问题、知识与技能、思维与表达、交流与反思等方面进行了阐述.

在课标案例22“跑道问题”中，跑道由左右两边均是半径为36m的半圆弧与两条直线段组成，如果能够计算出每条直道的长度，可以认为达到直观想象素养水平一的要求，能够利用直角坐标系写出跑道(上半部分)的解析式，可以认为达到直观想象素养水平二的要求；在案例29“估算地球周长”中，能够通过“立竿测影”的描述画出平面示意图，可以认为达到直观想象素养水平一的要求，能够借助平行线内错角相等的知识迁移或推理得出清晰的数与形之间的逻辑关系，进而得出地球周长，可以认为达到直观想象素养水平二的要求.再根据案例30“影子问题”，案例31“圆柱体截面问题”，不难将“直观想象素养水平一”理解为“数”与“形”之间的直译；“直观想象素养水平二”可以理解为“数”与“形”之间运用联想、知识迁移所反映出来的联系；“直观想象素养水平三”可以理解为“数”与“形”之间通过知识的创新性、数学分支之间及学科之间综合应用性所反映出来的“深层次”的联系.

因此，从上述对各个水平的总结与理解来看，特别是水平二、水平三，由于“数”与“形”之间运用联想角度、知识迁移的难易类别及数学知识点不同，采用的数学分支或所跨学科不同，往往存在同一情境与问题的同一直观图形中也会体现出不同的直观想象水平，同一水平也有不同的“知识与技能”、“思维与表达”方面的呈现方式.

课标中提到，数学学业质量水平二是高考的要求.包含了六大核心素养水平二阶段的综合要求，其中对直观想象的要求可概括为：能够想象并构建相应的几何图形，发现图形与图形、图形与数量的关系，探索图形的运动规律；能够掌握研究图形与图形、图形与数量之间关系的基本方法，借助图形性质探索数学规律，解决实际问题或数学问题；能够用图形探索解决问题的思路，形成数形结合的思想.

二、基于高考题探讨直观想象素养的各水平层次

接下来从直观想象水平划分的角度对2019年全国卷Ⅲ理数解析几何题进行案例探讨.解析几何的本质是用代数的方法来研究几何问题，所以解析几何是“数”与“形”结合的经典内容，借助“形”的直观来更有效地解决问题并没有否定“用代数的方法来研究几何问题”的本质.

(Ⅰ)证明：直线AB过定点;

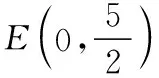
1.水平一的表现

图1

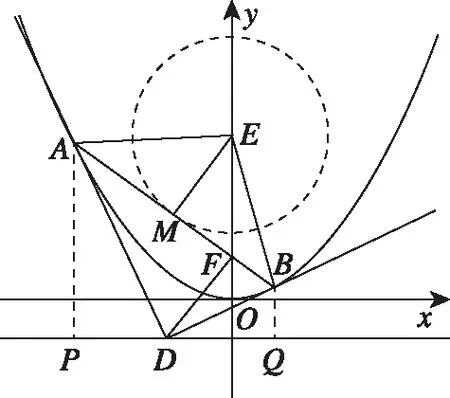
图2

2.水平二的表现

第(Ⅰ)问中若能利用求导公式、导数与斜率的关系，联想到切线DA,DB都过公共点D，以此求直线AB的方程，可以认为达到水平二的要求.具体回答如下：

2.1 表现形式一

知识与技能:利用EM与AB的斜率，根据弦长公式|AB|及点到直线AB的距离进而求得面积.

思维与表达:从直线出发，将直线代入抛物线方程

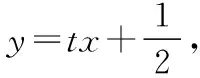
2.2 表现形式二

思维与表达:从点出发，利用向量与面积之间的关系

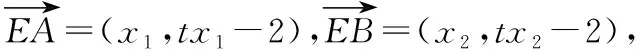
3.水平三的表现

是否可以基于以上情境与问题中的直观图形体现直观想象水平三的层次呢？笔者以为，第(Ⅱ)问如果从三角函数方面的相关知识结合图2利用参数法这个“创新”的角度得到解答，根据加分原则和满意原则，可以认为达到“水平三”的要求.主要思维与表达如下：

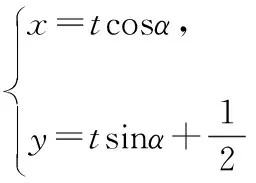
三、培养直观想象素养的备考启示

根据以上分析，水平一、二、三是直观想象素养的不同层次水平，在情境与问题、知识与技能、思维与表达、交流与反思等方面有相应的划分依据.事实上，往往存在同一情境与问题中会体现出不同的直观想象水平，同一水平也有不同的“知识与技能”“思维与表达”方面的呈现方式，所以备考中如何利用例题进行通性通法的解题教学，通过一题多解和多题一解让学生能解一题而通一类题，避免“会而不对、对而不全”的现象.因此，在教学备考中，首先要深刻把握各个核心素养的水平划分的内涵；其次要创设合理的情境，针对不同核心素养的不同水平设置问题；再次要利用好成熟的“直观模型”，例如几类特殊圆锥曲线图形模型、函数图形模型等；最后就是突出数形结合思想.