教学考试杂志社“优师计划”阶段性成果展示——高考重难点相关试题选登

1.已知函数f(x)为定义在R上的奇函数,且满足f(x+2)+f(x)=0,当x∈(0,1]时,f(x)=log2x,则f(log27),f(2 019),f(ln3)的大小关系为

( )

A.f(log27)>f(ln3)>f(2 019)

B.f(ln3)>f(log27)>f(2 019)

C.f(2 019)>f(ln3)>f(log27)

D.f(log27)>f(2 019)>f(ln3)

【答案】A

( )

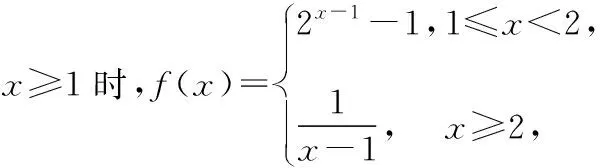
A.[-1,1)∪(1,3]

D.(-∞,-1]∪[3,+∞)

【答案】B

( )

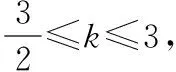
A.1 B.2

C.3 D.4

【答案】B

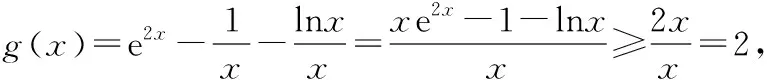
4.定义在R上的奇函数f(x)的导函数为f′(x),对∀x<0,均有xf′(x)-f(x)<0,则不等式(1-2x)f(x)+xf(2x-1)>0的解集为

( )

B.(-∞,0)∪(1,+∞)

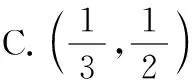
【答案】D

( )

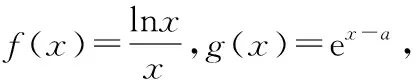
C.[1,e] D.(0,e]

【答案】B

( )

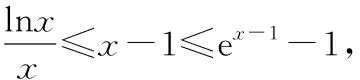
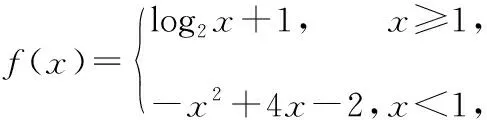
A．(3，+∞) B．(2，+∞)

C．(-∞，3) D．(-∞，2)

【答案】D

【解题分析】因为当x≥1时，f(x)=log2x+1是增函数；当x<1时，f(x)=-x2+4x-2也是增函数，且当x=1时有公共点，所以函数f(x)在R上是增函数.又因为f(1)=1，f(t-1)<1=f(1)，所以t-1<1,即t<2，故选D.

7.若函数f(x)=xlnx-ax2存在极值点，并且所有的极值点都小于2，则实数a的取值范围为

( )

【答案】B

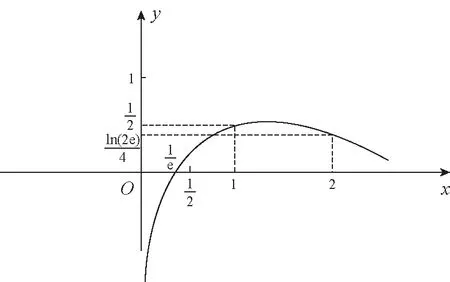
8.已知函数f(x)=ln|x|,若存在实数x使不等式f(x)≥x2-x-2a-2b-ln2成立，则实数a+b的取值范围为

( )

【答案】C

( )

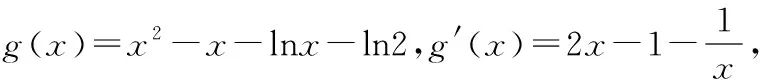
【答案】C

(Ⅰ)试讨论函数f(x)的极值的情况；

当00,f(x)在(0,2)上是增函数；

当x>2时，f′(x)<0,f(x)在(2,+∞)上是减函数，

∴当x=2时，f(x)有极大值,f(x)无极小值.

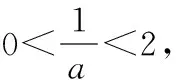
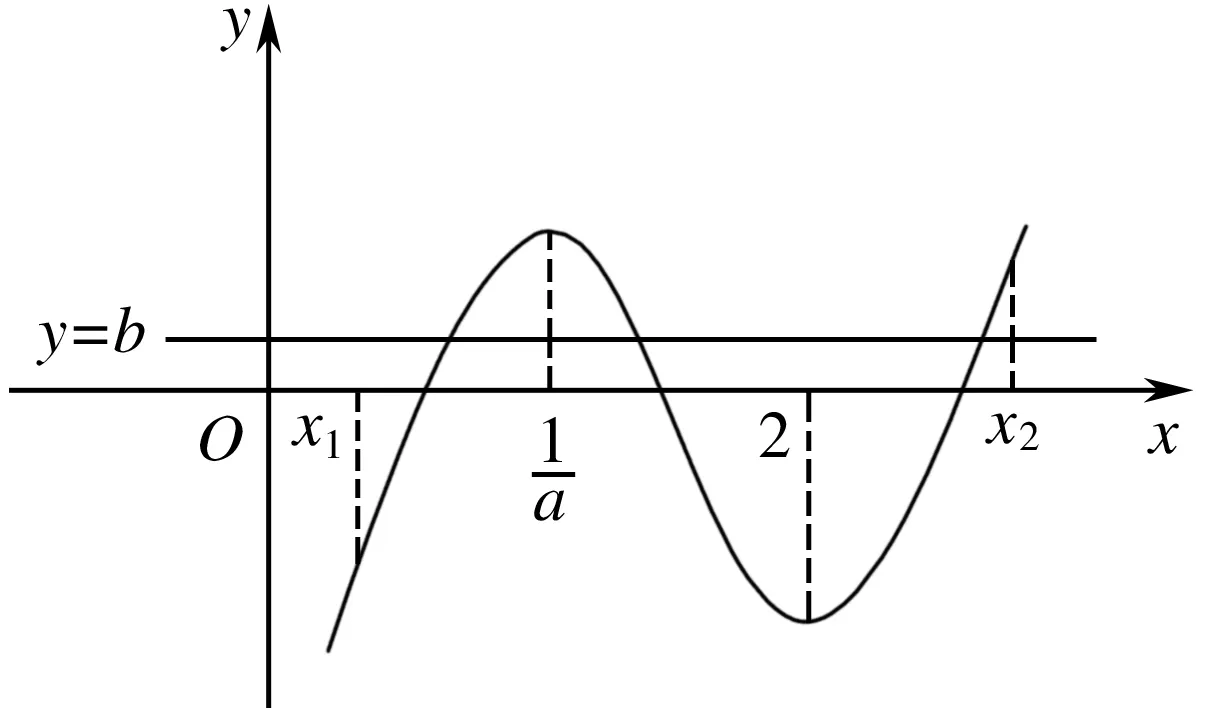
x0,1a 1a1a,2 2(2,+∞)f '(x)+0-0+f(x)↗极大值↘极小值↗

x(0,2)22,1a 1a1a,+∞ f '(x)+0-0+f(x)↗极大值↘极小值↗

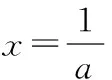
综上所述,当a=0时,当x=2时,f(x)有极大值,f(x)无极小值;

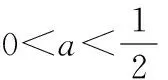
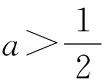
(6分)

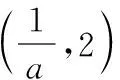
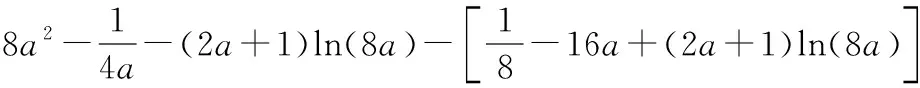
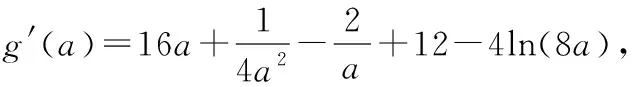
(12分)

11.(本小题满分12分)已知函数f(x)=ex(1+cosx)+a.

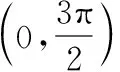
【解题分析】由题意可得f′(x)=ex(1+cosx-sinx).

(Ⅰ)∵当a=0时,f(0)=2,f′(0)=2,

(2分)

∴曲线y=f(x)在点(0,f(0))处的切线方程为 2x-y+2=0.

(5分)

(Ⅱ)令f′(x)=0,则1+cosx-sinx=0,

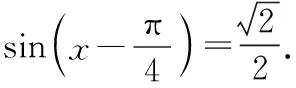
(6分)

(7分)

∴f′(x)>0,

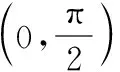
(8分)

∴f′(x)<0,

(9分)

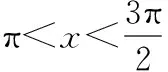
∴f′(x)>0,

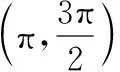
(10分)

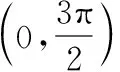
(11分)

(12分)

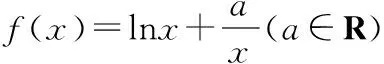
(Ⅰ)求实数a的值，并讨论f(x)的单调性;

(Ⅱ)设函数g(x)=ex·f(x)，证明：g(x)>1.

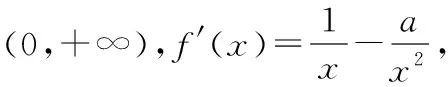
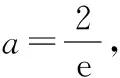
(3分)

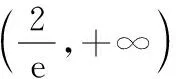
(5分)

(Ⅱ)证明:函数g(x)的定义域为(0,+∞),

(7分)

设h(x)=xlnx(x>0)，则h′(x)=lnx+1,

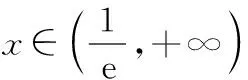
(9分)

所以当x∈(0,1)时，t′(x)>0，函数t(x)单调递增,

当x∈(1,+∞)时，t′(x)<0，函数t(x)单调递减,

(11分)

综上，在(0,+∞)上恒有h(x)>t(x)成立，

所以g(x)>1.

(12分)