混凝土单轴压缩短时蠕变破坏幂律行为研究

2020-11-13吴剑锋李慧剑王彩华孟德亮李佶芩

硅酸盐通报 2020年10期

吴剑锋，李慧剑，王彩华，孟德亮，李佶芩

(1.燕山大学河北省重型装备与大型结构力学可靠性重点实验室，秦皇岛 066004；2.东北石油大学秦皇岛校区，秦皇岛 066004)

0 引言

幂律规则是一种普适性规律，广泛存在于自然界的各种现象中。具有幂律分布的数据，在双对数图上呈现为斜率为幂指数的直线[1]。蠕变是材料在恒定应力作用下，应变随时间逐渐增加的现象[2](对于混凝土，当应力保持不变且长期作用时，常将该现象称为徐变)。对混凝土等准脆性材料的蠕变破坏幂律行为进行研究，将有益于解释该类材料的损伤演化机理和灾变破坏的预测[3-5]。郝圣旺课题组通过试验方法对岩石、混凝土等准脆性材料蠕变破坏的幂律行为开展了相关研究工作：杨雷[5]通过花岗岩蠕变破坏实验，发现应变加速度和应变率之间呈现幂指数α近似为2.0的临界幂律关系；周娜[6]通过混凝土单轴压缩蠕变试验，对混凝土试件在蠕变阶段轴线变形变化规律进行了分析，得出轴向变形变化率与时间近似成-2/3的幂律关系；刘超[7]通过对花岗岩的蠕变试验分析，发现轴向变形对时间的二阶与一阶微分关系之间存在幂指数α为2.0的幂律关系；Cheng等[8]通过花岗岩蠕变破坏实验，证实应变加速度与应变率之间呈现幂指数α近似为2.0的幂律关系。综上，研究对象多针对岩石，涉及混凝土蠕变破坏幂律行为的研究较少。

为此，本文将基于Voight经验公式对混凝土的蠕变破坏幂律行为进行研究，分析试样形状、配合比对混凝土单轴压缩短时蠕变破坏幂律行为的影响，探讨幂指数α与混凝土单轴压缩峰值应力、脆性指标、蠕变破坏强度、单位体积吸收能的关联，进而为混凝土蠕变性能的研究提供依据和参考。

1 混凝土蠕变破坏幂律行为理论模型

本文根据Voight[9-10]公式(见式(1))对混凝土蠕变破坏幂律行为进行研究。

(1)

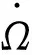
对式(1)变形并两边取对数，可以得出：

(2)

(3)

由式(3)可进一步得出：

(4)

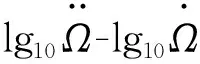
2 实验

水泥为秦皇岛浅野水泥有限公司生产的P·O 42.5(R)普通硅酸盐水泥；粗骨料来自秦皇岛抚宁的石灰岩碎石，粒径范围为10～16 mm；细骨料来自秦皇岛青龙的天然河砂，细度模数为2.79，普通中砂，最大粒径为5 mm。三种原材料的表观密度见表1。本研究配制B、C两种配合比，m水泥∶m水∶m砂子∶m石子分别为1.67∶1∶3.97∶6.48和2.05∶1∶3.86∶6.29。试验所需试样为100 mm×100 mm×300 mm棱柱体和100 mm×100 mm×100 mm立方体(对应编号为RLZB、RLZC、YLZB、YLZC，RLFB、RLFC、YLFB、YLFC，其中R代表蠕变、Y代表压缩，LZ代表棱柱体、LF代表立方体，B、C对应两种配合比)，所有试样均静水养护28 d，试验龄期180 d。

表1 原材料的表观密度Table 1 Apparent density of raw materials

试验加载装置采用上海衡翼精密仪器有限公司生产的HYWE-100060微机控制电液(伺服)万能试验机，试样变形采用钢铁研究总院钢研纳克检测技术有限公司生产的YYU-10/50电子引伸计测量。考虑到混凝土本身的离散性和试验时间，为实现蠕变破坏，采用单轴压缩分级加载短时蠕变方法。鉴于较高应力水平会使材料蠕变过程出现瞬时蠕变、稳态蠕变和加速蠕变三个阶段[11]，本文将混凝土试样单轴压缩峰值应力的70%作为蠕变试验初始预设目标应力，采用力控制加载模式，初始加载速度为2 kN/s，达到目标应力后，持荷1 200 s，若试样未破坏，则继续加载(级差为1 MPa，加载速度0.5 MPa/s，持荷时间仍为1 200 s)，以此类推，直至试样破坏。单轴压缩试验参照GB/T 50081—2016《普通混凝土力学性能试验方法标准》执行。

3 结果与讨论

3.1 蠕变破坏幂律行为分析

本研究选择应变ε为响应量，设计两种不同形状、两种不同配合比的试样对混凝土蠕变破坏幂律行为进行验证分析。图1为试样RLZB蠕变过程的lg10(d2ε/dt2)-lg10(dε/dt)曲线(为叙述方便，以下将d2ε/dt2简称为应变加速度,dε/dt简称为应变率)。

由图1可见，试样RLZB的应变加速度与应变率的双对数曲线呈线性演化趋势，并且该线性演化趋势呈现斜率近似为1.958的规律，这种线性行为可以近似表示为：

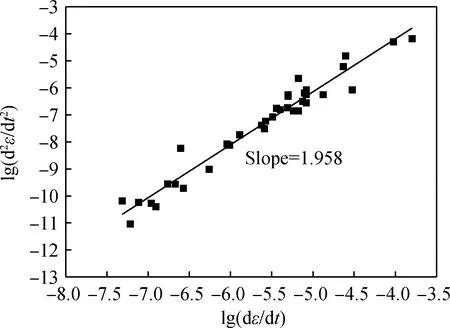
图1 试样RLZB的应变加速度与应变率双对数曲线Fig.1 Double logarithm curve of strain acceleration and strain rate of specimen RLZB

d2ε/dt2∝(dε/dt)1.958

(5)

由式(5)可知，试样RLZB蠕变过程的应变加速度与应变率之间存在符合式(1)描述的幂律关系，蠕变过程呈现出幂律行为，幂指数α为1.958。

上述验证过程表明混凝土蠕变破坏幂律行为理论模型可行。

其他试样的蠕变破坏幂律行为验证分析过程同上，蠕变过程的应变加速度与应变率之间亦同样存在符合式(1)描述的幂律关系，限于篇幅，不一一列出。各试样的幂指数α及其对比情况见表2和图2。

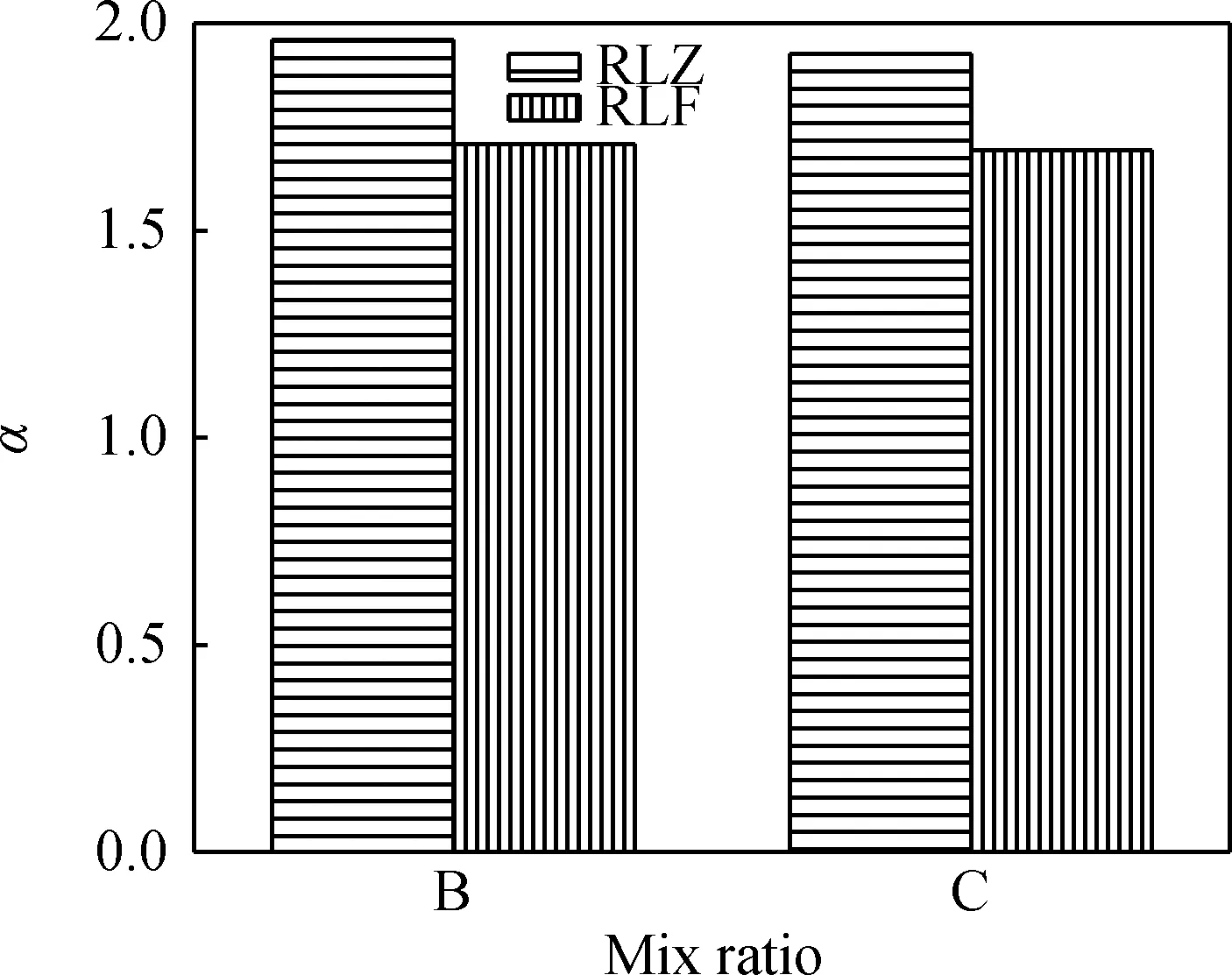
图2 试样形状及配合比对幂指数α的影响Fig.2 Effect of sample shape and mix ratios on power index

表2 各试样的α值、蠕变破坏强度、单位体积吸收能Table 2 Value of α, creep failure strength, unit volume absorption energy of each specimen

可见，棱柱体试样的幂指数α均比同配合比的立方体试样高，α值分别高出14.7%(对应配合比B)和13.8%(对应配合比C)；还可见，随配合比B、C的变化，同形状试样的幂指数α呈降低趋势，α值分别降低1.67%、0.8%。以上表明，试样形状、配合比的变化，不会改变混凝土蠕变破坏幂律行为的呈现，但会影响幂指数α的大小。

3.2 讨论

3.2.1 幂指数α与混凝土单轴压缩峰值应力的关系

单轴压缩峰值应力能够反映混凝土基本力学性能，可通过应力-应变曲线体现。图3为试样YLZB的单轴压缩应力-应变曲线，其他试样类同。本研究所用混凝土的单轴压缩峰值应力见表3，幂指数α与单轴压缩峰值应力的关系见图4。

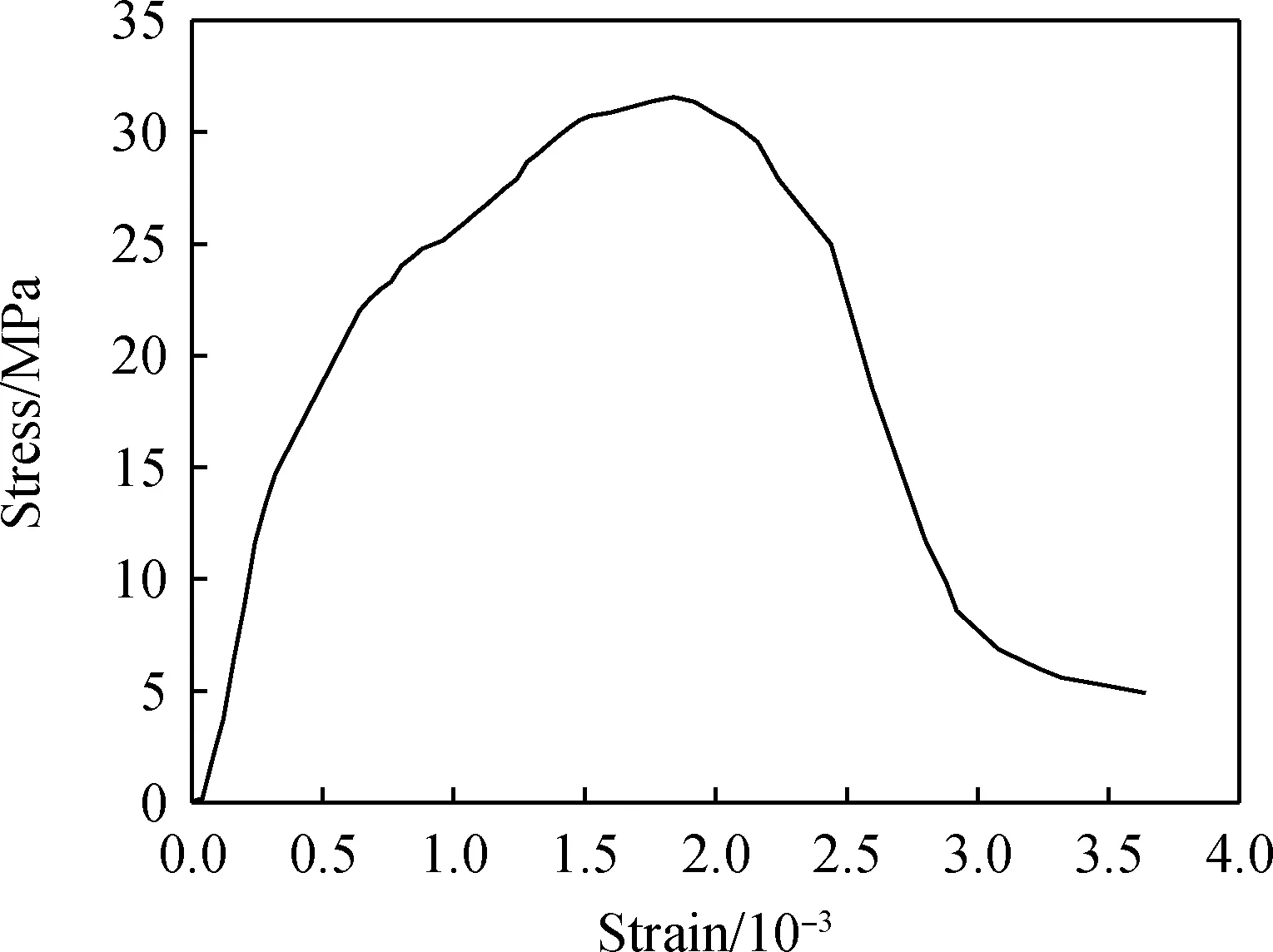
图3 试样YLZB单轴压缩应力-应变曲线Fig.3 Stress-strain curve of sample YLZB under uniaxial compression

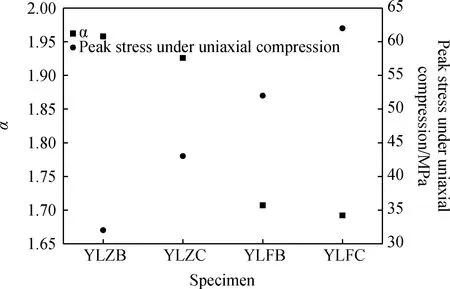
图4 幂指数α与单轴压缩峰值应力的关系Fig.4 Relationship between power index and peak stress under uniaxial compression

表3 各试样单轴压缩峰值应力、脆性指标Table 3 Peak stress and brittleness index of each specimen under uniaxial compression

可见，棱柱体的单轴压缩峰值应力分别低于同配合比的立方体38.46%(对应配合比B)和30.65%(对应配合比C)，随配合比B、C 的变化，棱柱体和立方体的单轴压缩峰值应力分别提高34.38%和19.23%，体现混凝土单轴压缩峰值应力与试样形状和配合比有关；此外，随混凝土单轴压缩峰值应力的提高，幂指数α呈降低趋势。

3.2.2 幂指数α与混凝土脆性指标的关系

脆性[12]是表征混凝土性能的重要指标之一。本文采用文献[13]给出的脆性指标来体现混凝土的脆性程度(计算方法见式(6))，并探讨了幂指数α与脆性指标的关联。本研究所用混凝土的脆性指标见表3，幂指数α与脆性指标的关系见图5。

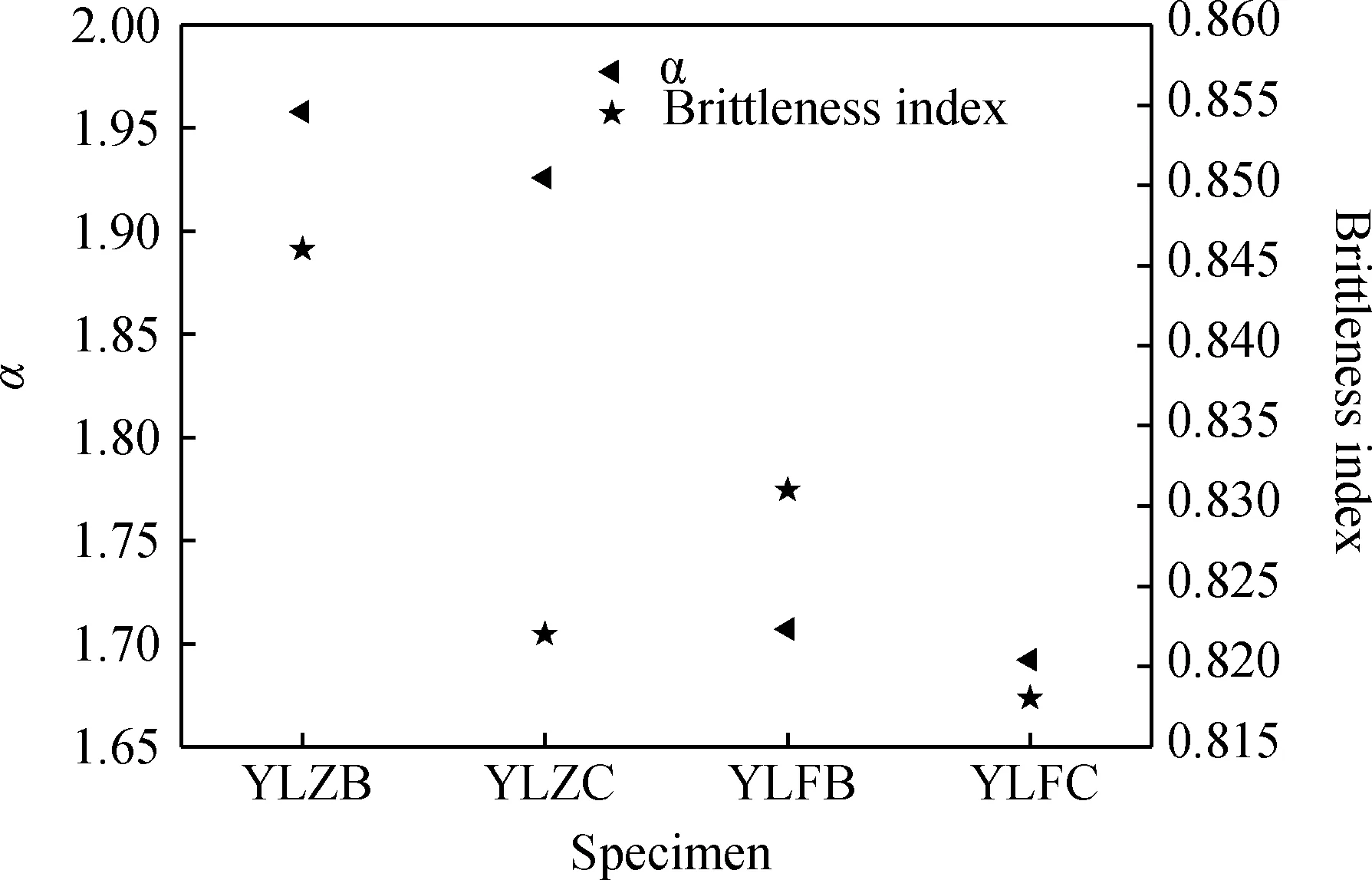
图5 幂指数α与脆性指标的关系Fig.5 Relationship between power index and brittleness index

B7=(σp-σr)/σp

(6)

式中:B7为脆性指标；σp为单轴压缩峰值强度；σr为单轴压缩残余强度。

可知，棱柱体的脆性指标分别比同配合比的立方体高出1.81%(对应配合比B)和0.49%(对应配合比C)，随配合比B、C 的变化，棱柱体和立方体的脆性指标分别降低2.92%和1.59%，表明混凝土脆性指标受到试样形状和配合比影响；又可知，随脆性指标的降低，同形状试样的幂指数α和同配合比试样的幂指数α均呈降低趋势。

3.2.3 幂指数α与混凝土蠕变破坏强度的关系

蠕变破坏强度能体现混凝土承担长期荷载的能力。各试样蠕变破坏强度见表2，幂指数α与蠕变破坏强度的关系见图6。

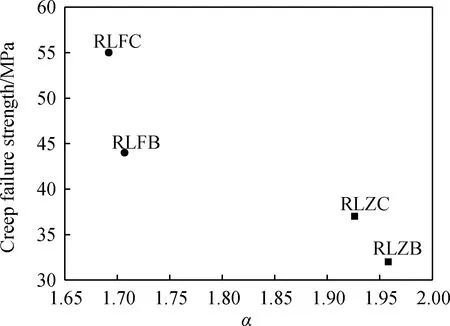
图6 幂指数α与蠕变破坏强度的关系Fig.6 Relationship between power index and creep failure strength

可以看出，棱柱体的蠕变破坏强度分别比同配合比的立方体低31.82%(对应配合比B)和32.73%(对应配合比C)，随配合比B、C 的变化，棱柱体和立方体的蠕变破坏强度分别提高23.33%和25%，说明混凝土蠕变破坏强度与试样形状和配合比有关；还可看出，幂指数α随混凝土蠕变破坏强度的提高而呈降低趋势。

3.2.4 幂指数α与单位体积吸收能的关系

材料破坏的本质是能量驱动下的失稳破坏[14]。本文对各试样蠕变过程的单位体积吸收能[15-16]进行了计算(具体计算方法见式(7))，并分析了单位体积吸收能与幂指数α的关联。各试样蠕变过程的单位体积吸收能见表2，幂指数α与单位体积吸收能的关系见图7。

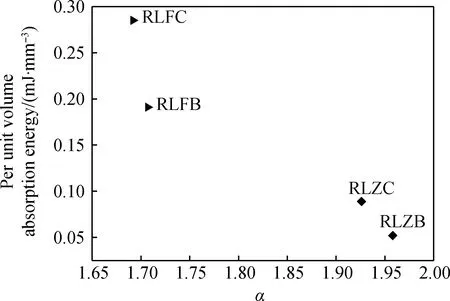
图7 幂指数α与单位体积吸收能的关系Fig.7 Relationship between power index and unit volume absorption energy

(7)

式中:W为试样的单位体积吸收能；F为试验力；u为试样轴向变形；V为试样体积。

可见，立方体试样的单位体积吸收能均比同配合比的棱柱体多，分别是棱柱体试样的3.67倍(对应配合比B)和3.2倍(对应配合比C)，随配合比B、C的变化，棱柱体试样和立方体试样的单位体积吸收能分别提高71.15%和49.21%，说明单位体积吸收能受到试样形状和配合比的影响；还可知，随单位体积吸收能的增大，幂指数α呈下降趋势。