对土方工程量计算方法精确性和适用范围的探讨
2024-01-03李璞LIPu刘东LIUDong
李璞LI Pu;刘东LIU Dong
(①东莞滨海湾新区管理委员会,东莞 523861;②东莞理工学院生态环境与建筑工程学院,东莞 523808)
0 引言
随着城市化的持续推进,城市逐步向外蔓延,所面对的地形地貌越来越复杂多变,需要处理的岩土工程问题也越来越多;同时,高层、超高层建筑越来越多,相应的其基坑越来越深,土方工程量在工程项目的总体工程量中的占比也越来越大。土方工程量的计算就是求取天然地面与设计地面之间填方或挖方的体积。[1]而目前,就土方工程量的计算方法,主要有方格网法、等高线法、平均断面法、DTM法等,面对不同的地形地貌,工程参与方若采用不同的计算方法,往往会得出不同的结果,其数值甚至相差较大,从而导致经济纠纷。为尽可能就土方工程量的计算定分止争,需要从理论上对各计算方法的精确性进行探讨,并探究各计算方法在实际操作层面的适用范围。
1 计算理论的精确性
1.1 方格网法
方格网法分四方棱柱体法和三角棱柱体法。
1.1.1 四方棱柱体法
四方棱柱体法就是将施工区域划分为若干个边长等于a 的方格网,每个方格网的土方体积V 等于底面积a2乘以四个角点高度的平均值。[2]如图1、图2 所示。

图1 四方棱柱体法
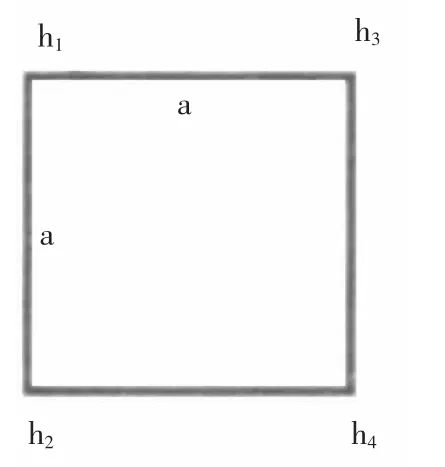
图2 全挖(或全填)
若方格四个角点部分是挖方、部分是填方时,则该公式的演绎形式为:
如图3、图4 所示。

图3 半挖半填

图4 三挖一填(或三填一挖)
用四方棱柱体法计算土方工程量,其本身从理论上就是一个近似计算公式,其精确计算的前提条件之一就是方格的四个角点在一个平面上。而在实际工程中,这一条件往往并不能满足。因此,用四方棱柱体法计算土方工程量,其计算值和实际值之间往往存在较大误差。当地形起伏越大,则误差也越大。[3]
为了减少土方工程量计算的误差,一般将整方格划分成多个三角形,土方工程量的计算方法相应地也由四方棱柱体法改成三角棱柱体法。
1.1.2 三角棱柱体法
三角棱柱体法就是将每一个方格顺地形的等高线沿对角线划分成两个三角形,然后分别计算每一个三角棱柱体的土方工程量。[2]当三角形为全挖或全填时:
如图5 所示。

图5 全挖或全填
当三角形有挖有填时,则其零线将三角形分成两部分,一个是底面为三角形的锥体,一个是底面为四边形的楔体。[2]其土方工程量为:
如图6 所示。
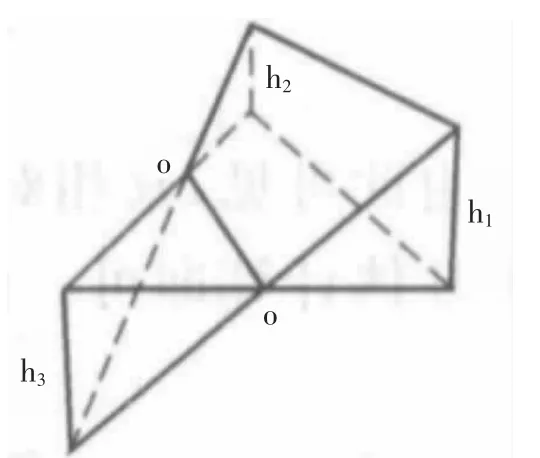
图6 有填有挖
由于三点确定一个平面,因此,上述三个用三角棱柱体法计算土方工程量的计算式就是精确计算公式,从理论上可以得到精确的土方工程量。现试举两例说明这一问题。
例1:某土方方格四个角点的标高如图7 所示,其边长a 为20m,试计算其土方工程量。

图7 土方方格四个角点的标高
①用四方棱柱体法计算,其土方工程量为:V=202(9+15+6+12)/4=4200m3。
②连接角点A1和C1;连接角点A 和C,用三角棱柱体法计算,其土方工程量为:V=202[(9+15+6)+(6+12+9)]/6=3800m3。
③连接角点B1和D1;连接角点B 和D,用三角棱柱体法计算,其土方工程量为:V=202[(9+15+12)+(6+12+15)]/6=4600m3。
三个计算结果差异巨大,但都不是精确值。实际上,该方格的四个角点就不在同一个平面上,其土方工程量就没有精确值。因为,对下底面为平面,而上底面不是平面的“四方棱柱体”,其体积的精确计算值就不一定是底面积乘以四条棱长平均值的积。对该例,现证明如下:
以D1点为原点,D1A1方向为X 轴、D1C1方向为Y 轴、D1D 方向为Z 轴,建立空间直角坐标系,则D、A、C 三点所确定的平面,其平面方程为6x+9y+20z-300=0。B 点的坐标为(20、20、12),将其代入该平面方程,显然,B 点不在该平面上。因此,该方格的四个角点D、A、B、C 不共平面,八个顶点D、A、B、C、D1、A1、B1、C1所构成的几何体并不是一个四方棱柱体。如图8 所示。

图8 建立直角坐标系
反之,若B 点的坐标为(20、20、0),即角点B 的标高为0,则该方格的四个角点D、A、B、C 共平面,那么采用上述三种土方工程量计算方法所得到的结果则是一致的,且是精确值3000m3。
那么,是不是四个角点共平面,采用四方棱柱体法计算的土方工程量就是唯一精确值呢?笔者的结论是不一定。现举下例说明该问题。
例2:某场地如图9 所示,试按挖、填方平衡的原则,分别计算挖方量和填方量。
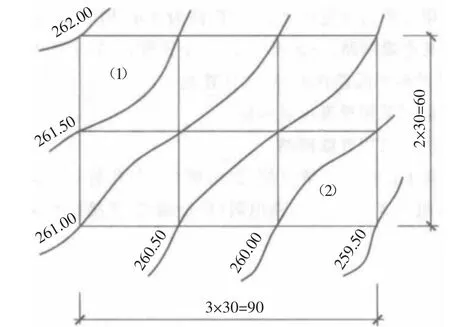
图9 场地各方格的角点标高
①计算设计标高。
各方格角点的施工高度如图10 所示。
②绘出零线。
很显然,零点A、B、C、D、E 为相应方格边线的中点,A、B、C、D、E 连线即为零线,且该零线为一条直线。挖方区和填方区构成以C 点为中心的中心对称图形。因此,挖方量和填方量相等。如图10 所示。
现设H11点所对应的设计标高点编号为(H11)',其余角点所对应的设计标高点编号类推。以(H11)'点为原点,(H11)'(H31)'方向为X 轴、(H11)'(H14)'方向为Y 轴、(H11)'(H11)方向为Z 轴,建立空间直角坐标系,则H11点的坐标为(0、0、1.25);H31点的坐标为(60、0、0.25);H13点的坐标为(0、60、0.25)。此三点所确定的平面,其平面方程为x+y+60z-75=0。如图11 所示。
经检验,H21、H12、H22、A、B、C、D、E 点均在该平面上,即该场地挖方区的天然地面方格各角点在一个平面上。可以证明,该场地天然地面的填方区方格各角点亦在该平面上,在此不予赘述。因此,将甲、乙、丙、丁、戊五个方格的挖方量求和,即可求出总的挖方量。
③计算挖方量。
1)甲方格如图12 所示。
采用三角棱柱体法计算:
连接角点H11和H22;连接角点(H11)'和(H22)',则甲方格关于平面H11H22(H11)'(H22)'对称,而被划分成两个挖方量相等的三角棱柱体。
或连接角点H21和H12;连接角点(H21)'和(H12)',甲方格即被划分成另两个三角棱柱体。
采用四方棱柱体法计算:
两种计算方法的结果一致。
2)乙、丙两方格的底面积、五个角点标高均一致。因此,该两方格的挖方量相等。现计算乙方格的挖方量。
采用三角棱柱体法计算:
连接A 点和H21、(H21)'点;连接B 点和H21、(H21)'点,则乙方格被划分成三个三角棱柱体,如图13 所示。三角棱柱体H21(H21)'H31(H31)'A 和H21(H21)'H22(H22)'B 的底面积、三个角点标高均一致。因此,该两三角棱柱体的挖方量相等。则该两三角棱柱体的挖方量之和为:

图13 乙方格(三角棱柱体法)
三角形H21AB 在设计地面的投影(H21)'AB 为等腰三角形。
三角棱柱体H21(H21)'AB 的挖方量为:
采用四方棱柱体法计算:
或仅连接B 点和H21、(H21)'点,则将乙方格划分为一个三角棱柱体和一个四方棱柱体,如图14 所示。

图14 乙方格(四方棱柱体法)
两种方法计算的结果不一致。很显然,两种方法,必有一种不精确或两种都不精确。
3)丁、戊方格土方工程量计算。
丁、戊两方格的底面积、三个角点标高均一致。因此,该两方格的挖方量相等。现计算丁方格的挖方量。
因此,该场地挖方量根据不同的计算方法有三种不同的结果。
采用四方棱柱体法计算:
采用三角棱柱体法计算:
④现延长EA,与X 轴相交与点G,可以证明H11H31的延长线与X 轴也相交于点G,且点G 的坐标为(75、0、0),如图11 所示。
由于天然地面各方格的角点和A、B、C、D、E 共平面,因此,该场地挖方量也等于大三棱锥H11(H11)'GE 的体积减去小三棱锥H31(H31)'AG 的体积。这是一个精确值。则:
该计算结果与采用三角棱柱体法计算的结果一致。因此,上述采用四方棱柱体法计算挖方量是不精确的。究其原因在于,分别采用四方棱柱体法和采用三角棱柱体法计算的乙或丙方格的挖方量存在误差。
乙或丙方格,其五个角点虽共平面,但分别采用三角棱柱体法和四方棱柱体法计算的挖方量结果仍差异巨大。由此得出结论:关于土方工程量的计量,采用三角棱柱体法可以得出精确值,而采用四方棱柱体法则不一定能得出精确值,即使天然地面方格的各角点共平面。
由于任何n 棱锥(底为n 边形)都可以划分为(n-2)个三棱锥,因此,根据祖暅原理,n 棱锥的体积和三棱锥的体积计算公式是一样的,即V=1/3SH(S 为底面积、H 为高)。而任何一个四方棱柱体都可以划分为多个三角棱柱体或三棱锥体,因此,任意方格的土方工程量理论上都可以运用三角棱柱体法求得其精确值。
1.2 等高线法
等高线法计算土方工程量就是利用地形图中的等高线计算测区范围内的土方体积。现行运用等高线法计算土方工程量的理论如下。
将两等高线之间所夹体积看成为台体体积,则第i 分层的体积为:
式中Si、Si+1分别为第i 分层的下底面积和上底面积;H 为等高距,其值在地形图上可以直接取得。[4]
然后将各分层的土方工程量相加求和即可。
上述计算公式只是一个近似计算公式,要利用等高线法计算土方工程量的精确值,就必须使用计算台体体积的精确计算公式。
而对同属于台体的棱台或圆台,设下底面积为S1,上底面积为S2,中截面面积为S0,H 为台体的高,则台体的体积为:
因此,应将上述土方工程量计算公式修正为:
1.3 平均断面法
如图15 所示,设基坑、基槽、管沟、路堤土体两端的横断面面积为F1、F2,L 为土体的长度,土体中截面面积为F0,则土方工程量为:[2]
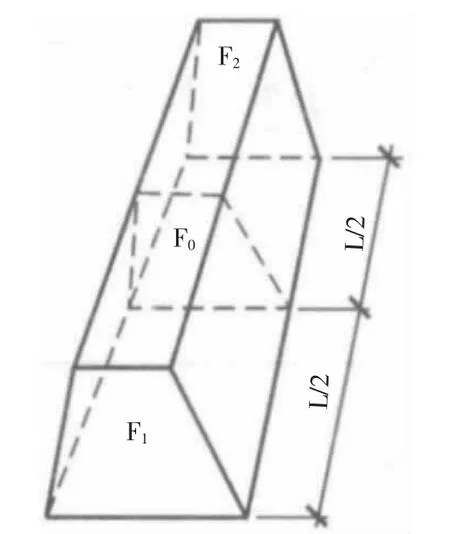
图15 平均断面法
该公式只是一个近似计算公式,完全精确的计算公式则为:
对于形状简单、规则且形状渐变的台体或基坑、基槽、管沟、路堤土体,中截面面积并不一定等于上下底面积或两端横截面积的平均值。因此,公式(8)、式(12)只能是近似计算公式。而运用等高线法或平均断面法计算土方工程量,本质上是一样的,都是计算台体的体积。因为,基坑、基槽、管沟、路堤可以看作推倒平放的台体。因此,等高线法和平均断面法的两个精确计算公式是等效的。
1.4 DTM 法
数字地面模型DTM(Digital Terrain Models)是通过计算机仿真和模拟技术,利用野外实测的地形特征数据建立与实地相似的数字化地面模型,是地表特征空间分布的数值的离散表现,是地形表面形态属性等多种信息的数字表示。地形表面形态属性信息一般包括高程、坡度、坡向等。[5]
DTM 法计算土方工程量就是利用实际测量的地形碎部点数据,按照一定的构网规则来形成空间三角网结构模型。在建立好的不规则三角网TIN(Triangulated Irregular Network)中,其每一个基本单元的核心是组成不规则三角形的三个顶点的三维坐标。[6]在天然地面的三角网中,从每个三角形的三个顶点竖直向下引出三条直线,直到与设计地面的三角网相交,这样便形成许多的三角棱柱体,这时整个待计算区域的土方工程量便是所有这些连续但不可微分的三角棱柱体的体积之和。如图16 所示。其中,三角棱柱体的上表面三角形ABC,即天然地面,用斜平面拟合;三角棱柱体的下表面三角形DEF 即设计地面,一般为规则或渐变的简单几何面的组合;三角形A1B1C1为三角棱柱体上、下表面在水平面上的投影。则该三角棱柱体的体积V=S△A1B1C1(HAD+HBE+HCF)/3。[7]而S△A1B1C1为三角形A1B1C1的面积,HAD、HBE、HCF分别为AD、BE、CF 的高度。
DTM 法计算土方工程量,其理论基础是运用公式求三角棱柱体的体积。因此,该方法理论上是可以求得其精确值的。
实际上,上述各种理论上的土方工程量精确计算公式都是基于土体为能用几何语言进行清晰、准确描述的形状简单、规则且形状渐变的情形,但在土方工程量计算的实际操作层面,土体的实际情况远不符该理想、标准状态,且不同计算方法对精确性的影响更有所不同。
2 实际操作层面不同计算方法的精确性
2.1 方格网法
该方法的一个潜在假设就是方格两顶点之间的坡度是均匀的,但实际情况往往并非如此。所以本方法一般适用于地形起伏不大、地面坡度有规律、范围比较大的场地平整时使用。
当地形图的比例尺越大、方格网边长越小、地形越平坦时,用该方法计算越精确,反之亦然。
2.2 等高线法
该方法一般适用于地形起伏较大、坡度变化较多的山坡地的土方工程量计算。但前提条件是等高线必须闭合,否则无法计算。
2.3 平均断面法
平均断面法一般适用于基坑、基槽、管沟、路堤等狭长土体的土方工程量计算。在实际操作层面,运用平均断面法计算土方工程量,其误差主要来源于横断面的不规则和地形的起伏。缩小误差的相应措施就是缩短相邻横断面的距离和在地形起伏的转折点处增加横断面。
2.4 DTM 法
DTM 法在构建的三角网中,直接把天然地面原始高程点当成格网的结点,能较好地与地形特征点、线相协调,逼真地表示复杂地形的起伏特征,能更好地适应复杂多变、不规则地形;同时用一个准确的数字化地面模型以提高计算速度。但其最终计算的精确性取决于TIN 模型的精确性,即对地形特征点、地形变换点数据采集的精确性、密度等。地形实际采样数据越密集,越能充分呈现出实际地形的细微变化,越能使土方工程量的计算值接近于实际真实值。其误差则来源于对这些地形实际原始数据采集、处理的方法和过程。
随着计算机技术的快速发展,基于TIN 模型的土方工程量计算发展前景广阔。譬如,李华蓉基于TIN 模型,引入三角形微分思想,将三角形按照一定规则进行分割,通过计算微分三棱柱体积,进行土方工程量的计算,进一步提高了其精确性;[8]金权基于TIN 模型,发展出一种改进的约束不规则三角构建算法,将场平工程区域边界作为约束,插入初始三角网,生成高精度的计算约束不规则三角模型,进而实现土方工程量的精确计算[9]等。
3 结束语
综上所述,由于天然地面的地形地貌千变万化,而设计地面可能是曲面、水平面、斜面或多种几何面的组合,将不规则地形地貌用规则几何形体进行计算模拟,其势必产生误差。所以,要完全精确地计算出土方工程量是不可能的。而较精确的土方工程量计算,对优选施工方案、正确选择工程施工机械、做好工程预结算和减少工程参与方之间的经济纠纷等都具有重要的实际意义。[1]无论从理论上,还是在实际操作层面,相较于其它几种方法,基于三角棱柱体体积计算方法的DTM 法,其精确性相对更高、适用范围更广。因此,在土方工程量计算中,应尽可能采用DTM 法。
