再生块体混凝土的单轴受压试验
2020-02-27蔡敏伟王卫华董毓利洪铁东陈香蓉郭秀泉
蔡敏伟, 王卫华, 董毓利, 洪铁东, 陈香蓉, 郭秀泉
(1. 华侨大学 土木工程学院, 福建 厦门 361021;2. 华侨大学 厦门市抗火综合防灾工程技术研究中心, 福建 厦门 361021)
20世纪90年代以来,我国面临许多钢筋混凝土结构的修复和拆除问题,由此产生大量的建筑废弃物,其中,废弃混凝土约占建筑垃圾的48.4%[1],合理利用废弃混凝土可以保护环境,减少固体废弃物排放,节约资源和能源.再生骨料孔隙率较高、初始裂缝多、吸水性大[2],与普通混凝土的力学性能差异较大.肖建庄等[3-4]、陈宗平等[5-6]针对再生骨料混凝土的受压力学性能进行研究.吴波等[7]将废弃混凝土拆解成特征尺寸为60~300 mm的块体混凝土[8],直接应用于构件中,形成再生混合混凝土构件,并进行静力和抗震性能的研究[9-11].张金锁[12]研究废弃混凝土块体的取代率、新旧混凝土的抗压强度差等因素对再生混合混凝土立方体试件抗压强度的影响.Wu等[13]发现当新旧混凝土抗压强度差较大时,废旧混凝土块体对再生块体混凝土抗压强度的影响较为明显,并提出抗压强度的预测公式.此外,吴波等[14]发现随着旧混凝土取代率的增加,试件组合抗压强度、弹性模量均呈降低趋势.刘春晖[15]发现在特征比不变的情况下,尺寸效应对再生混凝土立方体试件的弹性模量、峰值应变的影响可以忽略不计.目前,关于再生块体混凝土棱柱体试件受压力学性能的报道较为少见[12-15].基于此,本文对18个再生块体混凝土立方体试件和18个棱柱体试件进行单轴受压试验,分析不同因素对再生块体混凝土受压力学性能的影响.
1 试验概况
1.1 试件制作
制作18个再生块体混凝土立方体试件和18个棱柱体试件,每3个标准试件为1组,共分为6组立方体试件和6组棱柱体试件.
试件的设计参数,如表1所示.表1中:N为试件数量;l,b,h分别为试件的长、宽和高;fo为旧混凝土的抗压强度;η为旧混凝土的取代率;试件组编号Cu表示立方体试件,Pr表示棱柱体试件,R1~R3对应不同的旧混凝土的抗压强度,0~0.3对应不同的旧混凝土的取代率;Cu-R1-0,Pr-R1-0中旧混凝土的取代率为0,即新混凝土试件.
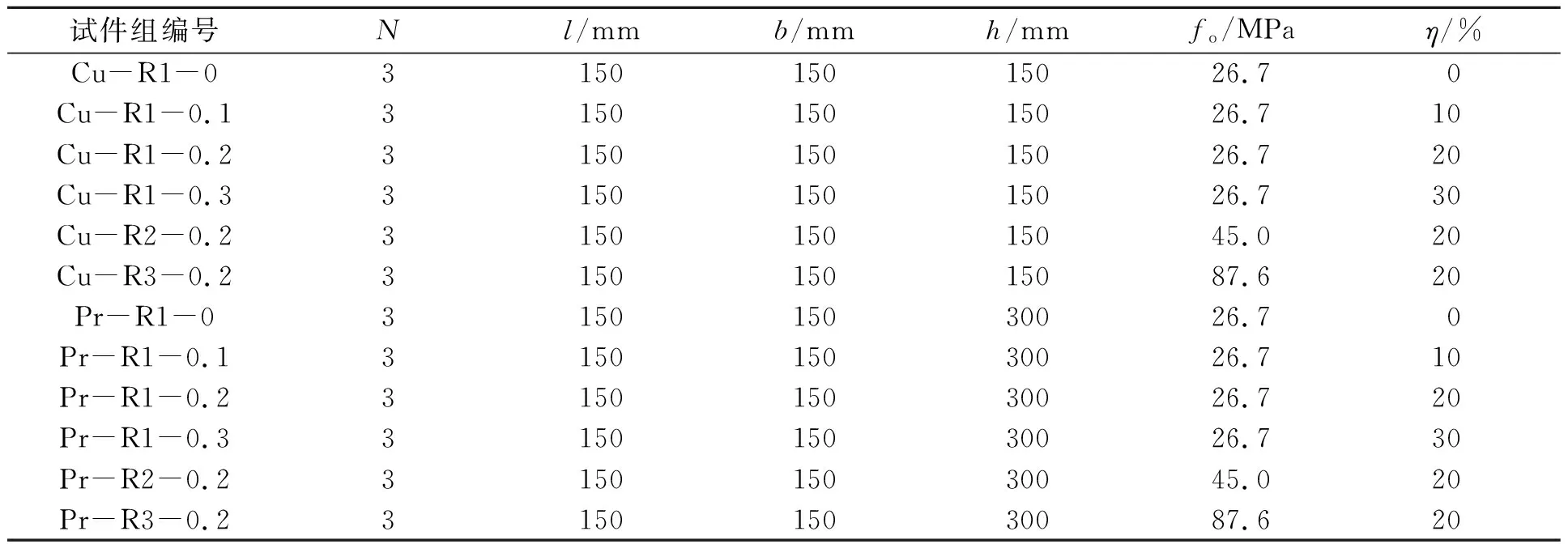
表1 试件的设计参数Tab.1 Design parameters of specimens

(a) 旧混凝土块体 (b) 试件的浇筑图1 旧混凝土块体和试件的浇筑Fig.1 Demolished concrete lumpsand casting of specimen
将废旧混凝土(剪力墙、梁和柱等)人工拆解成特征尺寸为50~60 mm的块体.选用抗压强度分别为26.7,45.0,87.6 MPa的3种旧混凝土块体.旧混凝土块体和试件的浇筑,如图1所示.在浇筑前,先将旧混凝土块体用网兜编号装好,置于自来水池内,提前充分浸泡24 h,使其吸足水分并洗净表面浮尘.在浇筑过程中,先在试模底部倒入一层厚度约为20~30 mm的新混凝土;然后,将旧混凝土块体与新混凝土交替放入试模内,充分振捣,使两者能充分接触.
新混凝土的抗压强度等级为C30,采用红狮牌42.5R普通硅酸盐水泥,碎石粒径为16.0~31.5 mm,坍落度为120 mm.
新混凝土的配合比,如表2所示.表2中:δ为含砂率;ρ为材料的用量.新混凝土的28 d立方体试件的抗压强度为42.3 MPa.

表2 新混凝土的配合比Tab.2 Mix proportions of new concrete
1.2 试验加载装置及加载制度
在华侨大学结构实验室SHT4206型电液伺服万能试验机上进行试验.试件的加载装置,如图2所示.图2中:棕黄色橡胶带用来固定声发射传感器探头.

(a) 立方体试件 (b) 棱柱体试件图2 试件的加载装置Fig.2 Loading setup of specimens
采用全程位移控制的加载制度,立方体试件的加载速率[16]为3 μm·s-1,棱柱体试件的加载速率为6 μm·s-1.为了测量棱柱体试件的弹性模量和泊松比,在沿试件高度的中轴线处粘贴混凝土应变片;在棱柱体试件上部左右对称布置两个高精度位移计,以记录试件的压缩变形;应变、荷载和位移则由计算机自动采集.
2 结果与分析
2.1 试验现象
在加载初期,立方体与棱柱体试件的表面未观察到裂纹开展;随着荷载的增加,试件表面逐渐出现细微裂纹.当荷载P为峰值荷载Pu的60%(P=0.6Pu)时,在立方体试件中部可观察到裂纹逐渐扩展,且伴有细小的开裂响声;当荷载达到峰值荷载(P≥Pu)后,立方体试件的裂纹发展变宽且较快,荷载突然降低而丧失承载力.当荷载为峰值荷载的60%~80%(P=0.6Pu~0.8Pu)时,棱柱体试件的裂缝首先在中部出现,与竖向约呈30°夹角斜向发展;随着荷载的增加,裂缝的长度和宽度逐渐增大,达到峰值荷载(P≥Pu)后,棱柱体试件中部可见明显裂纹,裂纹最宽处约为1.5 mm.再生块体混凝土试件的裂纹开展较稳定,破坏过程较缓慢,这一破坏过程与文献[17]的情况类似.
再生块体混凝土立方体试件和棱柱体试件的典型破坏过程,如图3,4所示.图3,4中:试件编码的最后一位数字对应每组的3个试件(1~3).

(a) 加载初期 (b) P=0.6Pu (c) P≥Pu (d) 试验结束 图3 立方体试件的典型破坏过程(Cu-R1-0.3-3)Fig.3 Typical failure process of cubic specimen (Cu-R1-0.3-3)

(a) 加载初期 (b) P=0.6Pu~0.8Pu (c) P≥Pu (d) 试验结束 图4 棱柱体试件的典型破坏过程(Pr-R2-0.2-3)Fig.4 Typical failure process of prism specimen (Pr-R2-0.2-3)
加载结束后,试块断裂面的典型破坏形态,如图5所示.由图5可知:添加低抗压强度旧混凝土的试件的新旧骨料界面难以辨别,新混凝土与旧混凝土结合良好;而添加高抗压强度(87.6 MPa)旧混凝土的棱柱体试件在新旧混凝土的结合界面上出现破坏现象.再生块体混凝土试件的破坏形态与新混凝土试件基本一致,都是形成两个近似对顶的角锥形状.

(a) Cu-R1-0-3 (b) Cu-R1-0.2-3 (c) Cu-R3-0.2-1 (d) Pr-R1-0-3 (e) Pr-R1-0.1-3 (f) Pr-R3-0.2-1 图5 试件断裂面的典型破坏形态Fig.5 Typical failure mode of fracture surfaces of specimens
2.2 抗压强度实测结果分析
参照文献[18],对不同参数下的每组3个标准试件的抗压强度取平均值,将其作为立方体试件的代表抗压强度fcu和棱柱体试件的代表抗压强度fc.各组试件抗压强度的相关参数,如表3所示.
由表3可以得到以下4点结论.1) 当新旧混凝土抗压强度差(46.2-26.7=19.5 MPa)相同时,随着旧混凝土的取代率从0增加至30%, 立方体试件与棱柱体试件的抗压强度均逐渐降低, 立方体试件的抗压强度下降20.1%,棱柱体试件的抗压强度下降32.8%.2) 当再生块体混凝土的取代率相同时,随着旧混凝土抗压强度的提高,立方体试件和棱柱体试件的抗压强度呈上升趋势,这与文献[19]在低抗压强度新混凝土中添加高抗压强度的旧混凝土块体而呈现的抗压强度值的增大规律一致.3) 当旧混凝土的抗压强度(45.0 MPa)与新混凝土的抗压强度(46.2 MPa)基本相同时,立方体试件的抗压强度比新混凝土试件略高,但棱柱体试件的抗压强度却比新混凝土试件略低.4) 再生块体混凝土棱柱体试件与立方体试件的抗压强度之比为0.78~0.83,平均值为0.80,小于新混凝土对比试件的比值0.94,该值仍比GB 50010-2010《混凝土结构设计规范》[20]要求的比值(0.76)略高,但与试件抗压强度换算公式相比,其值仍在安全范围之内.

表3 各组试件的抗压强度的相关参数Tab.3 Relevant parameters of compressive strength of each groups pecimens
再生块体混凝土由新混凝土和旧混凝土两部分混合组成,故组合的抗压强度与两者的混凝土抗压强度存在一定关系.文献[12-13]分别提出了不同的立方体试件的组合抗压强度公式,即
fcu,com,300=fcu,new,300(1-η)+fcu,old,300×η,
(1)
fcu,com,300=(fcu,old,300/fcu,new,300)0.86η×fcu,new,300(1-η)+(fcu,new,300/fcu,old,300)1.1η×fcu,old,300η.
(2)
式(1),(2)中:fcu,com,300表示边长为 300 mm 的立方体试件的组合抗压强度;fcu,new,300,fcu,old,300分别为边长为300 mm的立方体试件中新混凝土和旧混凝土的抗压强度.
式(1)适用于新旧混凝土的抗压强度差小于15 MPa的情况,式(2)适用于新旧混凝土的抗压强度差为41~86 MPa的情况[12-13].文献[14]将式(1),(2)应用于棱柱体试件,并建议将两式计算结果的平均值作为抗压强度的预测值.在文中新旧混凝土抗压强度差的范围内,立方体试件及经转换后的棱柱体试件的抗压强度皆采用式(1),(2)进行计算.
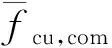
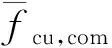
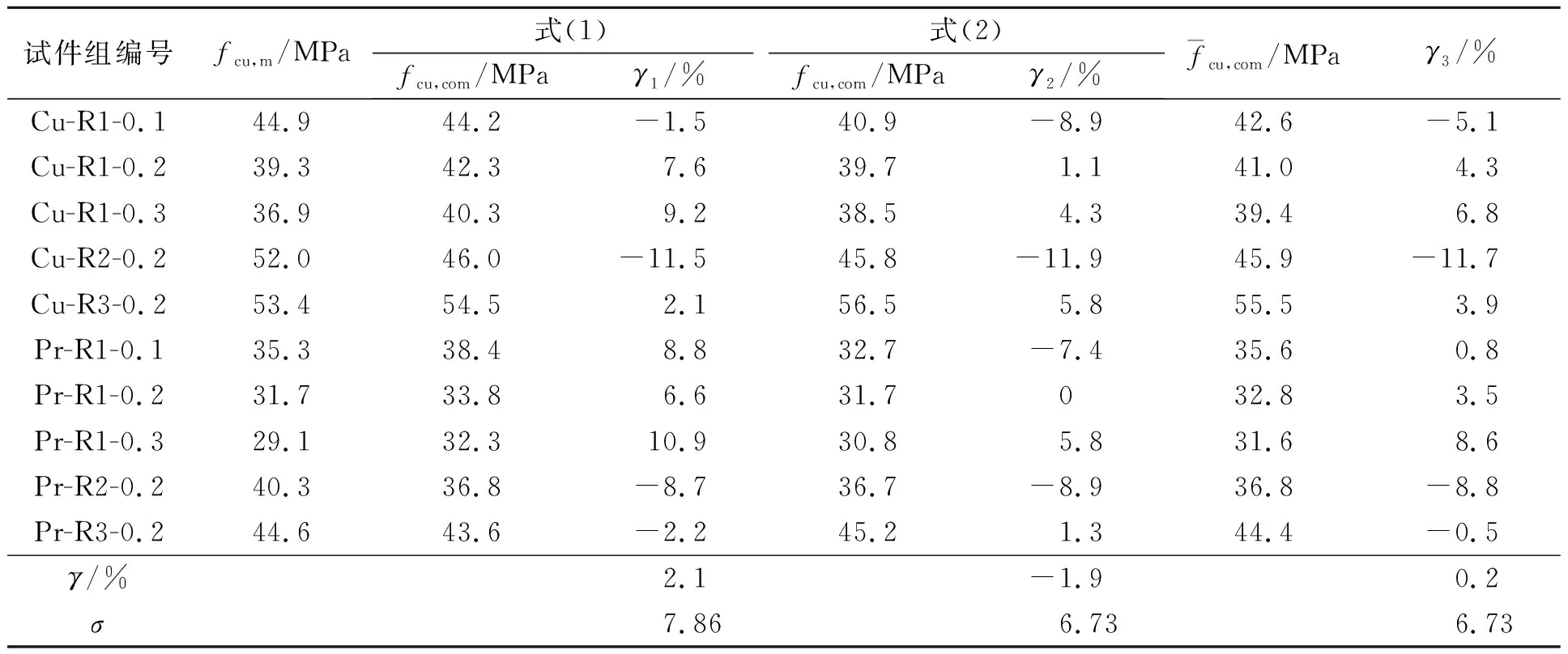
表4 抗压强度的计算值与试验值的对比Tab.4 Comparisons between calculated and measured compressive strengths
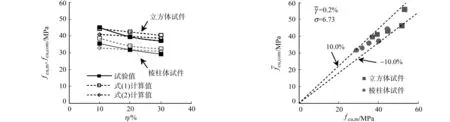
(a) 试验值与计算值 (b) 试验值与计算平均值图6 试件抗压强度的计算值与试验值对比Fig.6 Comparison of calculated results of specimens compressive strength with test results
2.3 弹性模量实测结果分析
将每组中3个棱柱体试件的弹性模量平均值作为该组再生块体混凝土的弹性模量的代表值.棱柱体试件组的实测结果,如表5所示.表5中:E为弹性模量;εmax为峰值应变;μ为泊松比;β,θ分别为峰值应力比和峰值应变比,即再生块体混凝土与新混凝土峰值应力或应变的比值.
由表5可以得到以下2点结论.1) 当新旧混凝土的抗压强度差相同时,棱柱体试件的弹性模量随取代率的增大而降低,当取代率从0增加至30%时,弹性模量降低11.9%左右.2) 当旧混凝土的取代率相同时,棱柱体试件的弹性模量与旧混凝土的抗压强度有一定的关系,添加比新混凝土抗压强度低(26.7,45.0 MPa)的旧混凝土试件的弹性模量比新混凝土试件组的弹性模量降低4.2%,6.1%,而添加抗压强度更高(87.6 MPa)的旧混凝土的试件组与新混凝土试件组的弹性模量基本相当.

表5 棱柱体试件组的实测结果Tab.5 Measured results of prism specimens
2.4 峰值应变实测结果分析
应力-应变曲线峰值处的应力对应的应变为峰值应变.由表5可知:棱柱体试件的峰值应变范围为1.913×10-3~2.238×10-3;取代率对棱柱体试件与新混凝土试件峰值应力比影响较大,当取代率从0增加至30%时,峰值应力下降33%,当取代率在10%以内时,取代率对峰值应变的影响较小,波动范围在12%内,当取代率超过10%后,峰值应力比和峰值应变比随着取代率的增加而下降,且下降趋势基本一致;添加高抗压强度的旧混凝土试件的峰值应变与新混凝土试件基本一致.
2.5 泊松比实测结果分析
由表5还可知:在弹性阶段,再生块体混凝土的泊松比范围为0.206~0.220,平均值为0.212,与普通混凝土的泊松比(0.180~0.220)相差不大;当新旧混凝土抗压强度差不变时,再生块体混凝土比新混凝土试件的泊松比略降,但差异不大;当取代率相同时,泊松比变化不大,且未呈现明显的变化规律.
3 结论
1) 当新旧混凝土的抗压强度差相同时,随着旧混凝土取代率的增加,再生块体混凝土的抗压强度、弹性模量均逐渐降低,且抗压强度下降得较为明显.当取代率从0增加至30%时,立方体试件的抗压强度下降20.1%,棱柱体试件的抗压强度下降32.8%,棱柱体试件的弹性模量降低11.9%.
2) 当旧混凝土的取代率相同时,随着旧混凝土抗压强度的增大,再生块体混凝土的抗压强度、弹性模量均呈一定的上升趋势.当旧混凝土的抗压强度与新混凝土基本相同时,立方体试件的抗压强度略高于新混凝土试件,但棱柱体试件的抗压强度却略低;当旧混凝土的抗压强度高于新混凝土时,立方体试件的抗压强度高于新混凝土试件,但棱柱体抗压强度的增幅不大.
3) 棱柱体试件与立方体试件的抗压强度之比为0.78~0.83,平均值为0.80,与现行规范公式的估算结果相比,其值仍在安全范围之内.
4) 当取代率超过10%后,峰值应力比和峰值应变比随取代率的增加而下降.在弹性阶段,再生块体混凝土的泊松比范围为0.206~0.220,平均值为0.212,泊松比变化不大,且未呈现明显的变化规律.
5) 在添加低抗压强度(26.7,45.0 MPa)旧混凝土的试件中,新旧混凝土结合良好,界面难以辨别;在添加较高抗压强度(87.6 MPa)旧混凝土的棱柱体试件中,新旧混凝土的结合界面出现分离现象.
