基于XFEM的孔洞对裂纹扩展路径影响分析

2020-11-13涂文锋赵士祥

南昌大学学报（工科版） 2020年3期

涂文锋，赵士祥

(南昌大学资源环境与化工学院，江西南昌 330031)

工程结构在制造过程中可能存在孔洞、夹杂等制造缺陷，此外基于机械紧固的需要，有时也要在机械构件上开孔洞，这些孔洞一定程度上会降低结构的承载能力，并对裂纹尖端的应力场产生扰动作用。在Ⅰ型加载条件下，处于扰动应力下的裂纹并不会沿垂直于Ⅰ型加载方向扩展，而是表现出复合型裂纹扩展的特性。准确的评估孔洞对于裂纹路径的影响，是机械结构可靠性研究的一个重要部分。

LUA等[1]使用混合边界积分的方法研究疲劳裂纹与孔洞、变形夹杂等微缺陷的弹性相互作用，采用包含复合型强度因子的富集单元表征动态裂纹尖端的奇异性以及孔隙夹杂等缺陷对裂纹尖端应力场的影响。Sukumar等[2]将数值方法与XFEM相结合，提出了一种无网格化的孔洞与材料夹杂的建模方法，对含孔洞、夹杂的疲劳裂纹扩展问题进行了研究。Shi等[3]采用了能动态更新裂纹前沿水平集数的快速计算方法，对近尖端塑性区历史状态变量进行有效积分，考虑裂纹闭合效应，实现了含孔洞的三维模型疲劳寿命预测。Ma等[4]通过开发的Abaqus子程序，考虑残余应力对裂纹扩展的影响，将残余应力的分布情况输入有限元模型中，对含有偏位孔的实验模型进行疲劳裂纹扩展路径模拟，验证了该程序的有效性，并评估最大切向应力准则预测裂纹偏离行为的准确性。Kumar等[5]采用虚拟节点扩展有限元法来模拟弯曲裂纹的扩展，用该方法实现了含孔洞平板试样裂纹扩展的模拟。高欣等[6]将一致性高阶无网格法拓展到非连续问题的数值模拟中，基于虚拟节点法描述间断位移场，并用该方法模拟含有3个孔洞的梁试样裂纹扩展路径。Boulenouar等[7]采用最大周向应力与应变能密度准则模拟了含有孔洞模型的疲劳裂纹扩展路径，结果表明2种准则所模拟的结果与实验结果有很好的吻合。近些年研究人员通过引入富集函数来模拟经典有限元法中的界面不连续，用于研究孔洞对动载荷作用下裂纹扩展路径的干涉作用[8-10]。此外孔洞尺寸和位置对裂纹尖端应力强度因子也有重要影响[11]，Zheng等[12]利用水平集数法追踪裂纹，该方法无需对有限元网格重新划分，实现了带孔平板准静态下裂纹尖端的应力强度因子的计算。王建明等[13]采用位移外推法并结合最小二乘法拟合得到含孔洞试样裂纹扩展过程中的应力强度因子。徐华等[14]采用圆形奇异区广义参数Williams单元，分析了孔洞位置和几何参数对Ⅰ～Ⅱ混合型裂纹尖端应力强度因子的影响。汪必升等[15]采用相互积分的方法，研究了非标带孔试样裂纹扩展过程中应力强度因子的变化规律。

虽然现有的文献已经证明孔洞对裂纹扩展路径有干涉，但是裂纹尖端的距离、孔洞的尺寸以及孔洞与初始裂纹尖端的夹角对于裂纹扩展路径偏转程度的影响很少定量的用某个参数来表示，并且含有孔洞试样的裂纹扩展路径偏转程度也很少与应力强度因子联系起来。本文提出挠度影响系数的概念来定量表示上述参数对裂纹扩展路径偏转程度的影响，此外通过计算应力强度因子建立挠度影响系数与载荷复合比之间的联系。

1 扩展有限元法与J积分理论

1.1 水平集函数

通常，在扩展有限元中用水平集函数来检测不连续边界。根据文献[2]，孔洞可视为不连续边界，孔洞边界上水平集值为0，包含孔洞边界的单元将用富集函数来描述。为了计算水平集函数，定义一个不连续域Ω，将指定区域分为2个不重叠的子域Ω+和Ω-，Г是孔洞的外形轮廓，定义xГ为孔洞外形轮廓边界上点，水平集函数Ф(x)可以表达为：

(1)

如图1所示，在Ω+这个区域内，水平集函数Ф(x)>0，在Ω-这个区域内，水平集函数Ф(x)<0，孔洞的外形轮廓Г上，Ф(x)=0。

1.2 扩展有限元离散形式

Sukumar等[2]提出了孔洞和裂纹的位移矢量函数，结合水平集法，通过添加附加位移场来模拟裂纹和孔洞这类不连续问题，图2为具有节点子集的离散域，位移函数Uh(x)：

(2)

式中：ui为有限元解的连续部分相关节点位移矢量；ai、bi、ci为富集单元节点自由度；nc为被裂纹完全分割的富集单元节点；nt为裂纹尖端富集单元节点；nh为孔洞周围的富集单元节点；Ni(x)为常规有限元的形函数形式；H(x)和F(x)分别为裂纹和孔洞的阶跃函数形式。

(3)

(4)

Φα是裂纹尖端的渐进函数，对于被裂纹分割的单元给出了渐近位移函数：

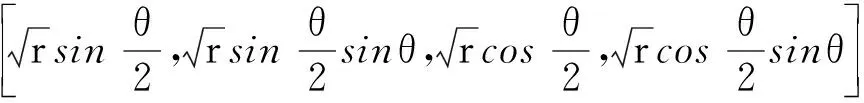
(5)

1.3 J积分与应力强度因子

J积分是建立在能量平衡方法基础上的一个断裂力学参数，可用于线性和非线性材料响应的情况分析，能够将裂纹扩展过程中能量释放速率G与裂纹尖端应力应变场强的强弱联系起来。如果材料的响应是线性的，可以建立J积分、能量释放速率G与应力强度因子的关系。J的轮廓积分定义为:

(6)

图3为裂纹尖端逆时针积分回路，Г是围绕裂纹尖端的任意轮廓，W是应变能密度，T是由外法线定义的牵引向量，n是法向单位矢量，u是位移向量。

Abaqus从6.10版本开始提供了一种基于Shih等[16]提出的虚拟裂纹扩展和区域积分法的J积分评估程序。如图4所示，裂纹尖端采用6节点CPS6

三角形网格和8节点CPS8四边形网格，根据裂纹尖端周围网格单元形成闭合回路来定义积分区域。对于复合型裂纹，使用相互积分的方法求解应力强度因子，从J积分中提取SIFs的实质在于确定G与SIFs的关系，即：

(7)

其中E′=E、E′=E/(1-v2)分别对应平面应力和平面应变状态。E、μ、v分别为杨氏模量、剪切模量和泊松比。

2 有限元模型及裂纹扩展模拟验证

如图5(a)所示，采用裂纹尖端附近含有圆形偏转孔洞的三维改进CT试样模型，试样厚度为3.8 mm，裂纹尖端与孔洞的距离为L，偏转孔中心与裂纹尖端的连线与过裂纹尖端X轴所成的夹角为θ，孔洞半径为R，上下加载孔的中心连线与初始裂纹尖端的距离a0=10.86 mm，以裂纹尖端为坐标系原点。材料的杨氏模量E=220 GPa，泊松比为v=0.31，在HyperMesh中完成CT试样主体部分的网格划分，裂纹扩展区域采用1:2过度的细化网格，近似尺寸为0.2 mm，长宽比为1。将夹具以离散刚体的方式建模，夹具表面与加载孔内表面分别为主从接触面，摩擦系数为0.01，“Normal Behavior”特性栏内选择“Hard Contact”硬接触。在上夹具上施加Pmax=4 kN，应力比R=0.1的常幅加载，加载方向竖直向上，下端夹具固定，约束夹具与试样的轴向位移为0。

为了验证扩展有限元法模拟裂纹扩展路径的准确性，选取文献[17]中如图5(b)所示的含3个加载孔的CTS试样在Abaqus进行建模，采用分步在加载的方式分别进行Ⅰ型、Ⅰ+Ⅱ型、Ⅰ型常幅加载，加载顺序及方向在图6(a)中表示。将模拟与实验结果对比，在Ⅰ型加载条件下，由于第3个加载孔的存在对裂纹尖端应力场的对称性产生干扰，模拟结果的裂纹扩展路径逐渐偏转，Ⅰ+Ⅱ型加载条件下，裂纹扩展路径逐渐偏转至基本垂直于加载方向，第3步Ⅰ型加载条件下裂纹有逐渐转化为Ⅰ型裂纹的趋势。模拟的裂纹扩展趋势与实验结果相近，验证了扩展有限元法的有效性。

3 孔洞对裂纹扩展路径的影响

3.1 孔洞与初始裂纹尖端的夹角θ对裂纹扩展路径的影响

建立如图5(a)所示有限元模型，裂纹尖端与孔洞的距离L=6 mm，孔洞半径R=3 mm，θ在0°到90°之间变化，为了定量表示孔洞对裂纹扩展路径偏转程度的影响，引入挠度影响系数C:

(8)

挠度影响系数定义为裂纹侵入点P(X′，Y′)的纵坐标绝对值与横坐标比值，在同组有限元数据中如果出现多个裂纹侵入结果，以侵入点横坐标最小值X′作为参照，未发生侵入的裂纹挠度影响系数的计算也以横坐标最小值X′作为参照。以第1组数据为例，当θ=0°时，侵入点横坐标为本组数据中的最小值X′=6 mm，求解本组有限元结果横坐标X′=6 mm对应的裂纹扩展路径纵坐标Y′，计算不同θ角下对应的挠度影响系数C。

第1组数据中裂纹路径分为侵入和不侵入孔洞2种情况，为了方便观察，将这2种情况下的路径分别在图8(a)、(b)中表示。当θ=0°时，由于孔洞位置关于X轴对称，因此孔洞的存在并没有改变裂纹尖端应力场的对称性，裂纹垂直于加载方向扩展直至侵入孔洞。θ≠0°时，孔洞存在对裂纹尖端的应力场的对称性有扰动作用，裂纹并非沿着垂直于Ⅰ型加载方向扩展，裂纹扩展路径先逐渐偏离X轴，一部分裂纹随后侵入孔洞，另一部分裂纹由于不足以被孔洞“吸引”侵入，在偏离X轴扩展一段长度后，裂纹尖端逐渐远离孔洞，孔洞对于裂纹尖端应力场的干扰能力逐渐降低，此后裂纹扩展路径逐渐向X轴靠拢，并且有转化为Ⅰ型裂纹的趋势。

θ增加到90°的过程中挠度影响系数呈现先增加后减小的趋势，当θ=45°时挠度影响系数取得最大值，当θ=0°时挠度影响系数为0，也就是孔洞对裂纹路径没有干涉作用。

3.2 孔洞与裂纹尖端的距离L对裂纹扩展路径的影响

本组有限元模型固定孔洞半径、孔洞与初始裂纹尖端的夹角θ不变，其中R=2 mm，θ=45°，L在4～7 mm之间，每间隔0.5 mm建立一个模型，L在8～12 mm之间，每间隔2 mm建立一个模型。

L从4 mm增加到6 mm，对应的5条裂纹扩展路径如图10(a)所示，当L=4、4.5 mm时孔洞距离初始裂纹尖端的距离较近，裂纹都侵入了孔洞。L≥5 mm时，孔洞对于裂纹路径的“吸引”能力不足以让裂纹发生侵入。如图10(b)所示，L=12 mm时，裂纹尖端逐渐接近孔洞时，孔洞对裂纹尖端应力场产生一定干涉，但由于孔洞半径较小且与裂纹尖的距离较远，干涉作用不足以使裂纹路径发生明显变化，裂纹沿垂直于Ⅰ型加载方向扩展。

随着L的增大，挠度影响系数C不断减小直至为0。值得注意的是L从4 mm增加到5 mm的过程中挠度影响系数C出现了很明显的下降，因此当孔洞与裂纹尖端的距离L较小时，挠度影响系数对L的变化较为敏感。

3.3 孔洞半径R对裂纹扩展路径的影响

为了研究孔洞半径对于裂纹扩展路径的影响，以孔洞到裂纹尖端的距离L=10 mm为例，孔洞与初始裂纹尖端的夹角θ=45°，孔洞半径分别为1、2、3、4、5、6 mm。

观察图12所示裂纹路径，当R=1 mm时，孔洞对于裂纹路径的干涉作用基本可以忽略。随着孔洞半径的增大，孔洞对于裂纹路径的“吸引”能力逐渐增强，对应的挠度影响系数C不断增大，当孔洞半径R=5、6 mm时，裂纹侵入孔洞。

3.4 L与R共同影响下的裂纹扩展路径

由前面的结论，减小孔洞与裂纹尖端的距离L或增大孔洞半径R都能增大裂纹挠度影响系数，为了探究L与R共同影响下裂纹路径挠度的主导影响因素，固定L/R=2，θ=45°，L分别为6、8、10、12、14 mm。

如图14所示，本组数据中裂纹扩展路径都侵入了孔洞。距离L与孔洞半径R同时增大，对应图15中的挠度影响系数却不断减小。由前面的结论θ和L一定，挠度影响系数应该随孔洞半径的增大而增大，由此可以得出结论固定L/R的情况下L是影响裂纹路径偏转程度的主导因素。

为了进一步验证该结论，设计了含有双偏转孔的改进CT试样模型，2个偏转孔分别位于第1、第4象限。双偏转孔的存在可以平衡或者削弱由单孔导致的裂纹尖端应力场的扰动，当裂纹尖端应力场的扰动作用无法得到平衡，裂纹扩展路径会偏向于具有更强“吸引”能力的孔洞。

分别取上述挠度影响系数相差较小和较大的2组孔洞来建模，孔洞与初始裂纹尖端的夹角θ=45°，L/R=2。如图16(a)、(b)中第1象限偏转洞半径分别为4、7 mm，与初始裂纹尖端的距离分别为8、14 mm，第4象限偏转孔半径都为3 mm，与初始裂纹尖端的距离都为6 mm。2种情况下虽然第1象限中偏转孔半径更大，但裂纹扩展路径都偏向于第4象限，由此可以验证上述结论的正确性。

4 载荷复合比Me与挠度影响系数的关系

由于裂纹尖端的应力场受孔洞影响而产生扰动作用，疲劳裂纹逐渐由Ⅰ型裂纹转变成复合型裂纹。为了研究该状态下裂纹扩展特性，采用围线积分的方式求解裂扩展过程中的应力强度因子K，引入载荷复合比Me来评估裂纹扩展特性。在研究复合型裂纹扩展问题时，载荷复合比Me是一个重要参数，用于表示复合型裂纹扩展过程中Ⅰ、Ⅱ型裂纹所占的比重。

(9)

求解相同横坐标X对应裂纹长度下的应力强度因子，目的是为了与挠度影响系数的定义相对应。

以3.3节裂纹扩展路径为例，在裂纹扩展过程中，KⅠ随着裂纹长度的增加而增大。孔洞半R=1 mm时，基本忽略孔洞对于裂纹路径的干涉作用，属于Ⅰ型裂纹，KⅡ≈0。当R=2、3 mm时，裂纹尖端由接近到远离孔洞的过程中，Ⅱ型裂纹所占比重先增大后减小。图18为裂纹扩展过程中载荷复合比的变化情况，当R=1 mm时Me≈1，当R≥2 mm时，在裂纹尖端侵入或者远离孔洞之前载荷复合比Me不断减小，且随着孔洞半径的增大，相同横坐标X对应的Me不断减小，这与挠度影响系数的变化趋势相反，对应的Ⅱ型裂纹比重不断增加。