夏热冬冷地区热桥对低层建筑能耗的影响
2020-11-13杜海存谢潇宇郭兴国刘向伟
杜海存,谢潇宇,郭兴国,刘向伟
(南昌大学a.机电工程学院,江西 南昌 330031;b.建筑工程学院,江西 南昌 330031)
热桥不仅对传统建筑能耗有较大的影响,对于节能建筑其能耗热量损失占建筑围护结构总能耗损失的比例更大,且在不断增加[1-4]。为了使夏热冬冷地区实现65%的节能目标,需要有效控制建筑能耗,而热桥对建筑能耗又有着显著的影响,故研究该地区热桥对建筑能耗的影响具有十分重要的意义。
国外关于热桥能耗的研究起步较早。Kosny等[5]和Kossecka[6]建立了等效墙模型。Aguilar等[7]通过对丁字热桥的能耗分析,验证了等效墙法的准确性。Martin等[8]进一步完善了等效墙热桥模型。Déqué等[9]、Purdy等[10]、Gao等[11]分别通过建立二维、三维热桥模型和运用等效U值等方法,提高了热桥能耗的计算精度。我国对夏热冬冷地区热桥能耗的相关研究起步相对较晚。南艳丽等[12-14]通过模拟和实验相结合的方法研究了热桥对围护结构能耗的影响。董孟能等[15]利用DOE-2从一维的角度分析了热桥对多、高层建筑的能耗的影响,得出了热桥面积百分比与建筑能耗的大小成正比的结论。李云等[16]通过研究热桥能耗的影响,提出了对夏热冬冷地区节能建筑中热桥的处理的原则。陶然等[17]利用ANSYS对实测墙体的温度场进行模拟,确定了热桥的影响范围。汪越等[18]利用有限元分析软件模拟出了混凝土框架柱热桥的温度场和热流场。贾殿鑫等[19-20]对热桥的影响范围及其评价指标等进行了研究。王明民等[21]比较了在相同环境下,外墙内、外保温中热桥对主体传热系数的影响大小。戴绍斌等[22]利用ANSYS软件研究了不同墙体保温体系的保温效果,最终得出外保温体系、热桥处理型自保温体系、内保温体系、自保温体系的保温效果依次减弱结论。吴卫等[23]建立了二维稳态热桥传热模型,并对不同类型剪力墙、填充墙搭接的楼板热桥节点进行了研究,得出有效阻断热桥节点可显著增强节能效果的结论。黄俊等[24]建立了二维稳态热桥传热模型并对不同保温体系下热桥的热损失进行了分析,发现了在外保温、内保温、自保温的体系下热桥处热损失会依次减少。王智等[25]建立了二维稳态模型并对建筑中烧结页岩多孔砖自保温外墙中典型的T形楼板热桥进行了模拟分析,确定了T形热桥处的无机保温砂浆层覆盖范围的最优值。张举等[26]详细计算夏热冬冷地区一体化系统中膨胀螺栓和各种龙骨对系统传热的影响,并对如何降低热桥能耗提出了具体方案。阮方等[27]对分室间歇用能情况下居住建筑围护结构的保温影响区域进行了研究,分析了人行为和容忍温度对保温节能的影响。何琛等[28]分析了热桥对间歇供暖房间的影响。沈张等[29]利用COMSOL软件建立了二维和三维的热桥模型,确定了不同保温材料的适用范围。朱赛鸿等[30]建立了二维热桥传热模型,并利用ANSYS软件分析了不同墙体构造、窗框材质等8种因素下,墙体内部等温线和热流量的分布、外墙窗洞口的内表面温度等参数。吴锋等[31]利用CFD对自保温体系下外墙转角处热桥的传热情况进行分析,计算结果表明,热桥内表面在冬季时会发生结露现象,防止结露需采相应的保温措施。张欣苗[32]建立了三维热桥传热模型,并利用GAMBIT和Fluent计算了热桥的热损失,研究表明热桥对围护结构建筑能耗影响较为显著。
综上所述,目前就夏热冬冷地区热桥能耗的研究主要是对各部分子热桥进行单独建模,并对子热桥模型传热情况进行分析,忽视了热桥传热的相似性与整体性,鲜有对同类热桥如丁字热桥进行整体建模的研究。而且对热桥能耗分析时往往只考虑空气温度与热桥间对流换热所产生的影响而忽略了土壤温度与热桥间对流换热以及太阳辐射换热对热桥能耗的影响。
本文建立起包括外墙-屋顶、外墙-中间层楼板、外墙-地面3处丁字热桥的整体热桥模型,考虑土壤温度以及辐射换热对二维热桥传热模型的影响,通过THERM和Design Builder计算了建筑的负荷,并以此来分析夏热冬冷地区热桥对低层建筑能耗的影响。
1 热桥模型
1.1 数学模型
1.1.1 模型假设
1) 建筑材料同性匀质且为常物性。
2) 导热过程始终为稳态。
3) 内部无热源且考虑辐射换热影响。
4) 不考虑湿传递及热湿相互作用。
5) 墙体相邻材料间接触紧密,忽略接触热阻的影响。
1.1.2 热桥传热模型
二维热桥模型的传热计算以如下稳态二维热传导公式为基础。
(1)
式中:T为温度,K。
二维热桥模型内部任意2种材料交界面的热流密度q用式(2)计算
(2)
式中:q为总热流密度,W·m-2;λ为材料的导热系数,W·m-1·K-1;ex、ey分别为相邻的2种材料交界面处的单位法向量在x和y方向的分量。
二维热桥模型墙体外表面的热流密度和换热系数分别用式(3)和式(4)计算
q=qc+qr
(3)
式中:qr、qc为受辐射换热和受对流换热影响产生的热流密度,W·m-2。
(4)
式中:h为墙体的换热系数,W·m-2·K-1;ΔT为传热界面两侧的温度差,K。
1.1.3 边界条件
绝热墙体、屋顶两者的外表面同时受到太阳辐射和空气对流换热的影响。假设天空由阴天和晴天2个区域构成。那么太阳辐射的影响通过外部平均辐射温度来表示。
Eex=σTrm
(5)
式中:Eex为外表面所受黑体辐射力,W·m-2;σ为斯忒藩为玻尔兹曼常数,5.669 3×10-8,W·m-2·K-4;Trm为太阳辐射造成的表面温升温度,K。
(6)
式中:Fgd、Fsky为热桥外表面到地面的视角因子(分别是地平线以下区域)与天空;fcir为天空中晴朗部分的因子;Jsky为天空中晴朗部分的光能传递,W·m-2;Tw为室外温度,K。
qr=hr(Tw-Trm)
(7)
式中:hr为受辐射换热影响下的换热系数,W·m-2·K-1。
(8)
式中:ε为总半球发射率。
室内表面对流换热主要通过自然对流,室外表面对流换热主要通过强制对流
qc=hc(Tw-Te)
(9)
式中:hc为受对流换热影响下的换热系数,W·m-2·K-1;Te为墙体外表面温度,K。
地面和中间层楼板两者分别与室内空气的接触面,和地面与土壤的接触面,这3类都属于第3类边界条件,如式(10)、式(11)所示。
(10)
(11)
式中:Tn为室内温度,K。
其他断面按绝热边界计算,如方程(12)所示。
(12)
1.2 几何模型
利用THERM建立起包含外墙-屋顶、外墙-中间层楼板、外墙-地面3处丁字热桥的二维热桥模型如图1所示。
2 负荷计算
将THERM计算出的夏、冬两季墙体的传热系数分别设为kx和kd。保持墙体中水泥砂浆层和砌体空心砖层厚度不变,通过方程(13)调整绝缘层(松散矿棉)δ2的厚度,使得利用Design Builder计算冷、热负荷时墙体的平均传热系数分别设置为kx和kd,并计算出新的冷、热负荷。
(13)
式中:k为墙体的传热系数,W·m-2·K-1;kx、kd为夏季、冬季墙体的传热系数,W·m-2·K-1;Ri、Re,R分别为墙体的内、外表面热阻以及墙体热阻,m2·K·W-1;hi、he分别为墙体内、外表面换热系数,W·m-2·K-1;λ1、λ2、λ3分别为水泥砂浆层、矿棉层和砌体空心砖层的导热系数,W·m-1·K-1;δ1、δ2、δ3分别为水泥砂浆层、矿棉层和砌体空心砖层的厚度,mm。
3 模拟对象及参数
以某二层居住建筑为研究对象,层高3.0 m,建筑面积约220 m2。室内温度:冬季293.15 K,夏季299.15 K。2个季节各选取1个计算日进行负荷计算。通过Design Builder建立三维建筑模型。热桥各层的材料物性参数如图1(b)和表1所示[23-33]。根据主要城市室外气象设计计算参数以及张慧智等[34]对中国土壤温度的季节性变化及其区域分异的相关研究,得到了南昌、成都、武汉、上海4个地区夏季和冬季的室外空气温度及土壤温度,如表2所示。
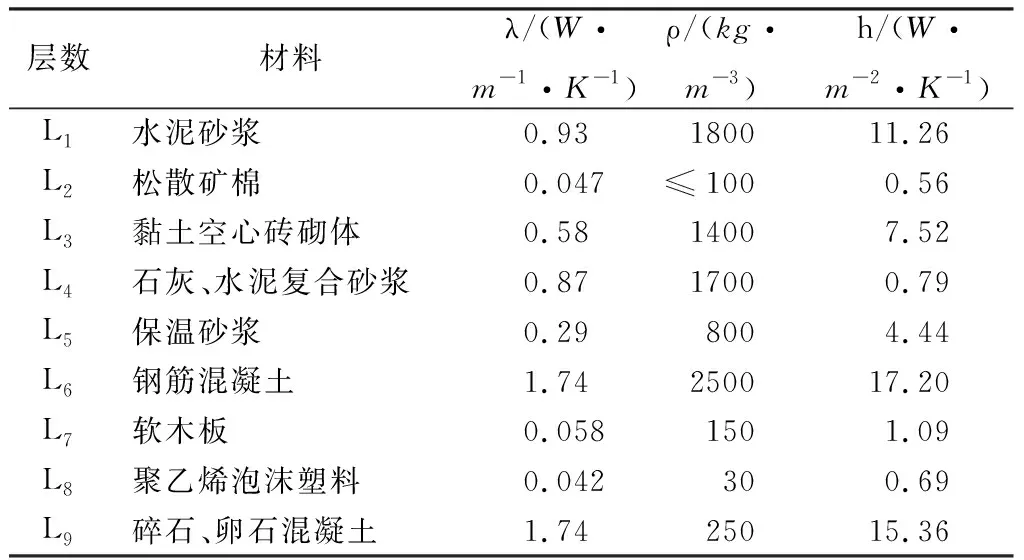
表1 材料物性参数Tab.1 Material property parameter
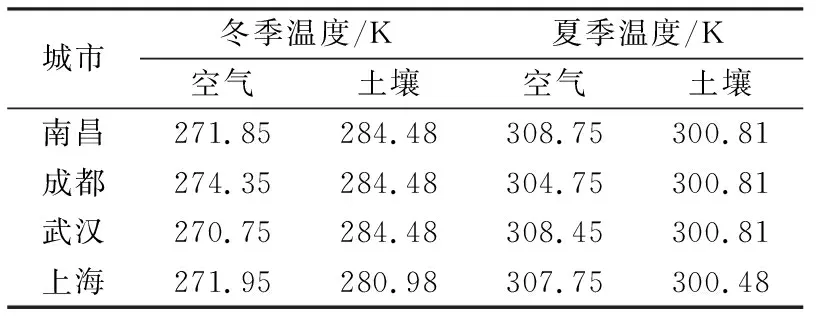
表2 室外空气温度及土壤温度参数Tab.2 Outdoor air temperature and soil temperature parameters
4 模拟结果分析
如图2所示,夏、冬两季外墙-屋顶、外墙-中间层楼板、外墙-地面3处丁字热桥的热流密度均大于单独外墙处的热流密度,且夏季热流方向从外到内而冬季则从内到外。
利用THEAM建立二维热桥模型,根据表2的室外参数条件,计算出该建筑位于南昌、成都、武汉、上海4个地区有热桥与无热桥2种情况下墙体的平均传热系数,并进行对比研究。如表3所示,在无热桥情况下,夏、冬两季的平均传热系数不变,这是因为没有考虑到屋顶、中间层楼板以及地面对墙体传热的影响,而有热桥情况下室外条件(包括室外空气温度以及土壤温度)会对屋顶、中间层楼板以及地面的传热造成较大的影响,进而影响墙体传热,改变其平均传热系数。
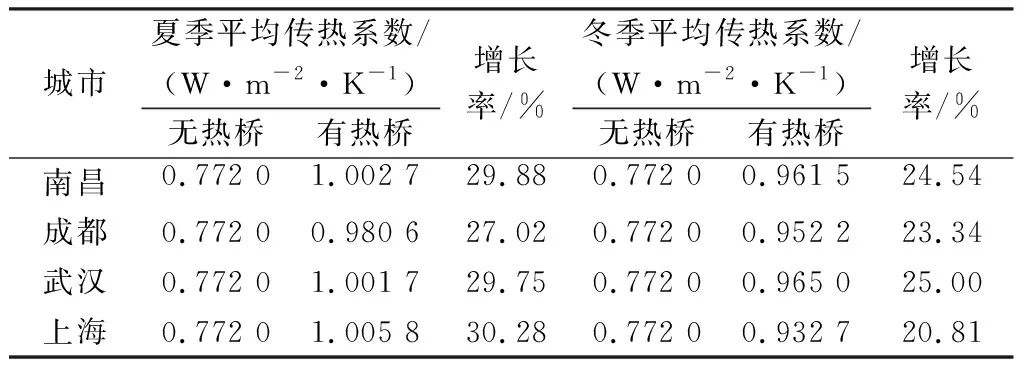
表3 墙体平均传热系数Tab.3 Average heat transfer coefficient of the wall
在考虑热桥影响后,夏季墙体平均传热系数增大27.02%~30.28%。冬季墙体平均传热系数增大20.81%~25.00%。其中成都、武汉、南昌3个地区夏季平均传热系数逐渐增加,这是因为三者属于同一土壤温度分区,土壤温度相同,平均传热系数主要受室外空气温度的影响。夏季时墙体平均传热系数随着室外空气温度的增加而增加,而冬季时墙体平均传热系数则会随着室外空气温度的降低而增加。
夏季时上海地区室外空气温度比武汉低0.7 K,而其最终平均传热系数增长率却高于武汉0.53%,这是因为上海地区土壤温度比武汉低0.33 K,使得外墙-地面处热桥的换热增强,最终导致其外墙的平均传热系数大于武汉。同样冬季时上海地区的室外空气温度与南昌相近,但由于上海地区土壤温度比南昌低3.5 K,故其外墙-地面处热桥的换热强度较小,最终导致其外墙的平均传热系数增长率比南昌低3.73%,分析可得墙体的平均传热系数不仅受室外空气温度的影响还受土壤温度的影响。
如表4所示,在考虑热桥影响后,建筑冷负荷增大3.36%~4.63%,建筑热负荷增大6.49%~7.76%。其中成都、武汉、南昌3个地区夏季冷负荷增长率逐渐增加,这是因为三者属于同一土壤温度分区,土壤温度相同,夏季冷负荷增长率主要受室外空气温度的影响,所以冷负荷增长率会随着室外空气温度的增加而增加,而冬季时热负荷增长率则会随着室外空气温度的降低而增加。
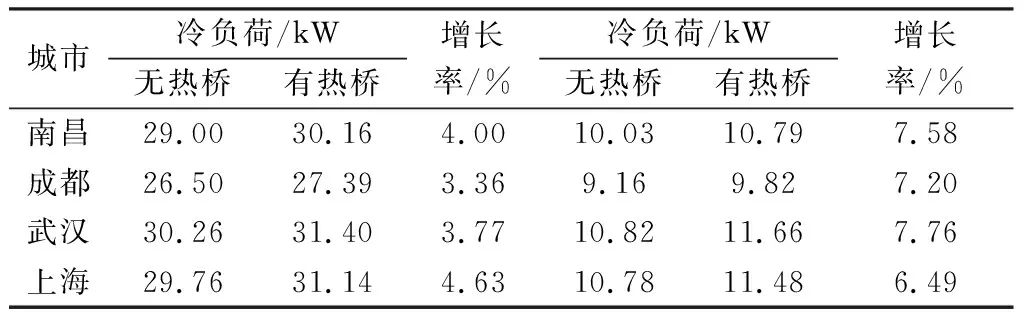
表4 2种情况下冷、热负荷Tab.4 Cooling and heating load in two case
夏季时上海地区室外空气温度比武汉低0.7 K,而其最终冷负荷增长率却高于武汉0.86%,这是因为上海地区土壤温度比武汉低0.33 K,使得外墙-地面处热桥的换热增强,最终导致其冷负荷增长率大于武汉。同样冬季时上海地区的室外空气温度与南昌相近,但由于上海地区土壤温度比南昌低3.5 K,故其外墙-地面处热桥的换热强度较小,最终导致其冬季热负荷增长率比南昌低1.09%,分析可得建筑负荷不仅受室外空气温度的影响还受土壤温度的影响。
室外空气温度与土壤温度都对墙体平均传热系数有较大的影响,下面进一步比较两者对墙体平均传热系数的影响大小。以南昌地区气候为例(如表2),夏季:室外空气温度35.6 K,土壤温度27.66 K;冬季:室外空气温度-1.3 K,土壤温度11.33 K。根据控制变量法,设置了4个对照组,依次为:增加1、1.5 K;减少1、1.5 K。以表3中南昌地区有热桥时计算的平均传热系数:夏季1.002 7 W·m-2·K-1,冬季0.961 5 W·m-2·K-1为标准。计算了室外空气温度或土壤温度单独作用时墙体的平均传热系数及其增长率如表5所示。
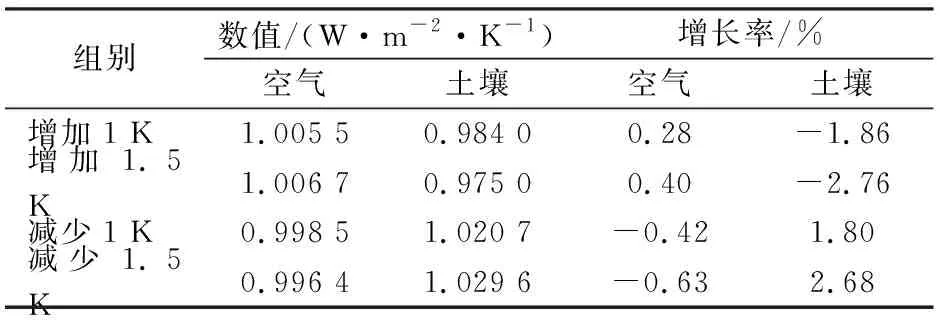
表5 对照组的平均传热系数及其增长率Tab.5 Average heat transfer coefficient and growth rate of the control group
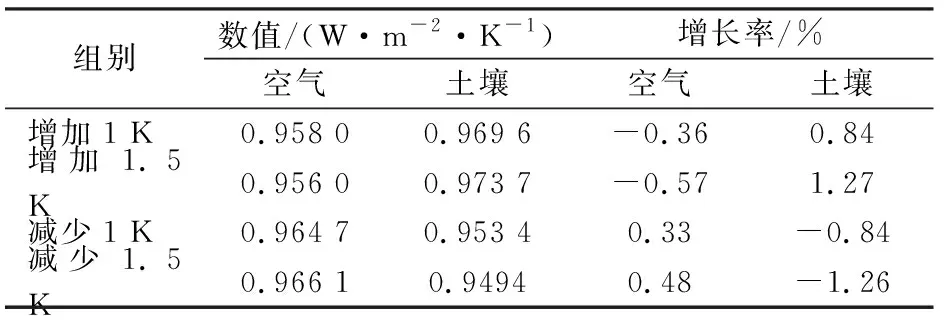
表6 对照组冬季平均传热系数及其增长率Tab.6 Winter average heat transfer coefficient and growth rate of the control group
无论夏季还是冬季,在其他因素相同的情况下,土壤温度对墙体平均传热系数的影响均大于相同变化量下室外空气温度对墙体平均传热系数的影响。
5 结论
1) 考虑热桥后墙体平均传热系数增长率大于建筑负荷的增长率,其中夏季:墙体平均传热系数增大27.02%~30.28%,建筑冷负荷增大3.36%~4.63%;冬季:墙体平均传热系数增大20.81%~25.00%,建筑热负荷增大6.49%~7.76%。
2) 同一季节与城市下,负荷变化与墙体平均传热系数变化成正相关。故若要研究某因素对建筑负荷的影响,可以先研究其对平均传热系数的影响。
3) 室外空气温度和土壤温度均会对墙体的平均传热系数造成较大的影响,在其他条件相同且两者变化量相同的情况下土壤温度对墙体平均传热系数的影响大于室外空气温度。
