纳米尖阵列屏蔽效应与发射面积耦合机理仿真

张晶园，刘昌祎，黄向东，张 妮，李菁波，张 涛

(1.西安科技大学 电气与控制工程学院，陕西 西安 710054；2.西安科技大学 机械工程博士后流动站，陕西 西安 710054;3.西安科技大学 理学院，陕西 西安 710054)

0 引 言

随着工业化水平的不断发展，针对真空度、电离度以及气体浓度等物理量的传统检测方式在某些领域已经无法适应新的要求。近年来，随着碳纳米管[1-2]、氧化锌纳米线[3-4]和硅纳米线[5-6]等新型材料被相继挖掘，纳米材料进入高速发展阶段[7-8]。此类材料特有的尖端尺度和长径比能够在较低的电压下产生较高的场增强因子[9]，有望实现低电压下的电子发射与气体电离，从而形成气体放电。这为新型场致电离器件提供了物质基础[10]。基于此类器件的真空规，电离源和电离式气体传感器等可通过对放电电流的检测，实现对真空度、电离度和气体浓度等物理量快速、准确的测量。在某些对采样频率和采样精度要求较高的环境下，基于场致电离器件的各类元件展现出了极大的应用潜力。

微电晕放电是指发生在电极间隙为亚毫米以下量级，且所处空间为极不均匀电场中的一种局部自持放电现象[11-12]，场致电离器件基于电晕放电原理，通过器件的输出电流对极板空间内的物理参量进行感知。文献[13]对碳纳米管的场发射特性进行了建模分析，指出碳纳米管的密集排布会造成严重的屏蔽效应，不利于放电电流的形成。文献[14]对发射器(纳米尖端)的场发射特性进行了分析，指出空间电荷会沿着发射器进行分布，所有这些电荷都会对发射器尖端的场产生影响，进而影响发射器之间的屏蔽。文献[15]模拟了板-棒结构下气体放电的动态过程，指出了单管模型放电时电子的动态分布情况。但上述研究主要在多纳米尖端的静电场和单纳尖端动态电场方面进行研究探讨，其结论在多纳米尖动态电场是否符合还犹未可知，且在多纳米尖和动态电场下研究屏蔽效应还可以对场致电离器件的放电电流进行提升。通过仿真计算，得到动态电场下不同尖端间距的等势线分布图及电子密度分布图，对动态电场下的屏蔽效应做出进一步说明，并以优化其内部关键结构参量即屏蔽效应与发射面积间耦合关系的方式来提高板-棒结构纳米尖阵列的放电电流，这对场致电离器件输出性能的提升有着非常重要的意义。

基于流体-化学动力学混合方法[16-18]，建立二维微场域板-棒结构电晕放电模型，在常温常压下以N2-O2混合气体为背景气体进行建模仿真。重点研究放电过程中的碰撞电离[19]及二次电子发射[20]等物理过程，为提高场致电离器件的输出电流，探究屏蔽效应与发射面积之间的耦合关系及其对放电电流的影响。

1 场致电离器件工作机理

场致电离器件利用纳米尖端特有的尖端尺寸与长径比，能够在纳米尖端附近产生较高的场增强因子，进而使电子在器件内部获得能量从而去碰撞气体分子，进而发生碰撞电离并产生新的电子(α过程)。电离出的电子在电场中获得能量从而延续碰撞电离，形成电子雪崩。产生的电子在电场的作用下定向移动(漂移过程)形成放电电流。在这个过程中，电离产生的正离子会在电场中获得能量并不断轰击纳米尖表面产生二次电子发射(γ过程)，进而不断为电离反应提供种子电子，从而使放电过程得以维持[21]。具体工作原理如图1所示，其中μe和μi分别为电子和离子的迁移率，De和Di分别为电子和离子的扩散率。

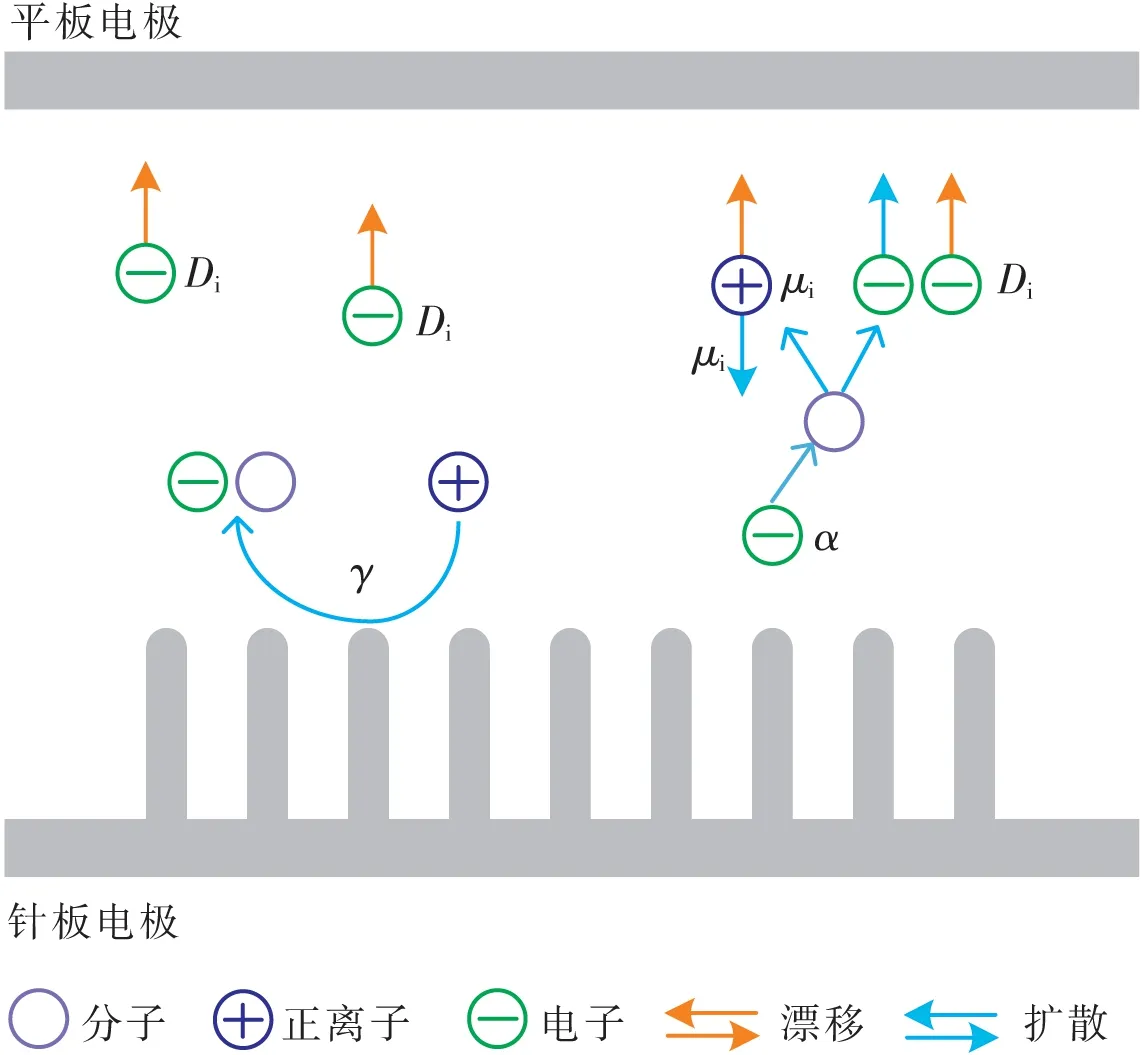
图1 场致电离器件工作原理

由于纳米线是生长在基底上的线状尖端，半径为纳米级别，高度为微米级别，且在基底上的分布较为均匀。因此笔者将此类线状尖端统称为纳米尖端，生长着此类尖端的电极称为纳米尖电极，以便后续描述。

2 仿真模型的建立

2.1 控制方程

传统的流体动力学控制方程通常是由电子、正负离子连续性方程和泊松方程构成[22]。文中在此基础上加入等离子体化学反应模型，并且在仿真中加入电离反应、重离子反应、碰撞反应以及纳米尖表面的二次电子发射过程。基于此对N2-O2混合气体放电空间进行仿真。

控制方程为

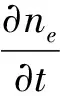
(1)

Γe=-(μe·E)ne-De·ne

(2)

(3)

式中ne，Γe,Qe，μe,De分别为电子的密度、通量、净生成率、迁移率和扩散率；t为时间,s；E为电势,V；M为使电子数变化的反应个数之和；xj和kj分别为方程式j中目标物质的摩尔分数和化学反应速率；Nn为中性粒子密度。

电子动量方程为

(4)

式中me,ue,Pe分别为电子的质量、漂移速率和压力张量；q为核电荷数；vm为电子动量的传递碰撞频率。

重粒子连续控制性方程为

(5)

jk=ρzwkVk

(6)

式中ρz为总混合物粒子数密度；wk，jk，Zk，Vk分别为粒子k的质量分数、扩散通量、反应速率和多分量扩散速率；um为质量平均流体速度矢量。

泊松方程为

-·ε0εrU=ρb

(7)

式中ε0为真空介电常数；εr为相对介电常数；U为电压，V；ρb为表面电荷密度。

2.2 等离子体反应类型

文中仿真以空气作为空间电离气体，因此将背景气体中N2和O2之比设置为4∶1。仿真共添加了11种物质之间的25个反应，具体的化学反应式[23]见表1，其中1～5为电子碰撞反应，6～19为重粒子反应。

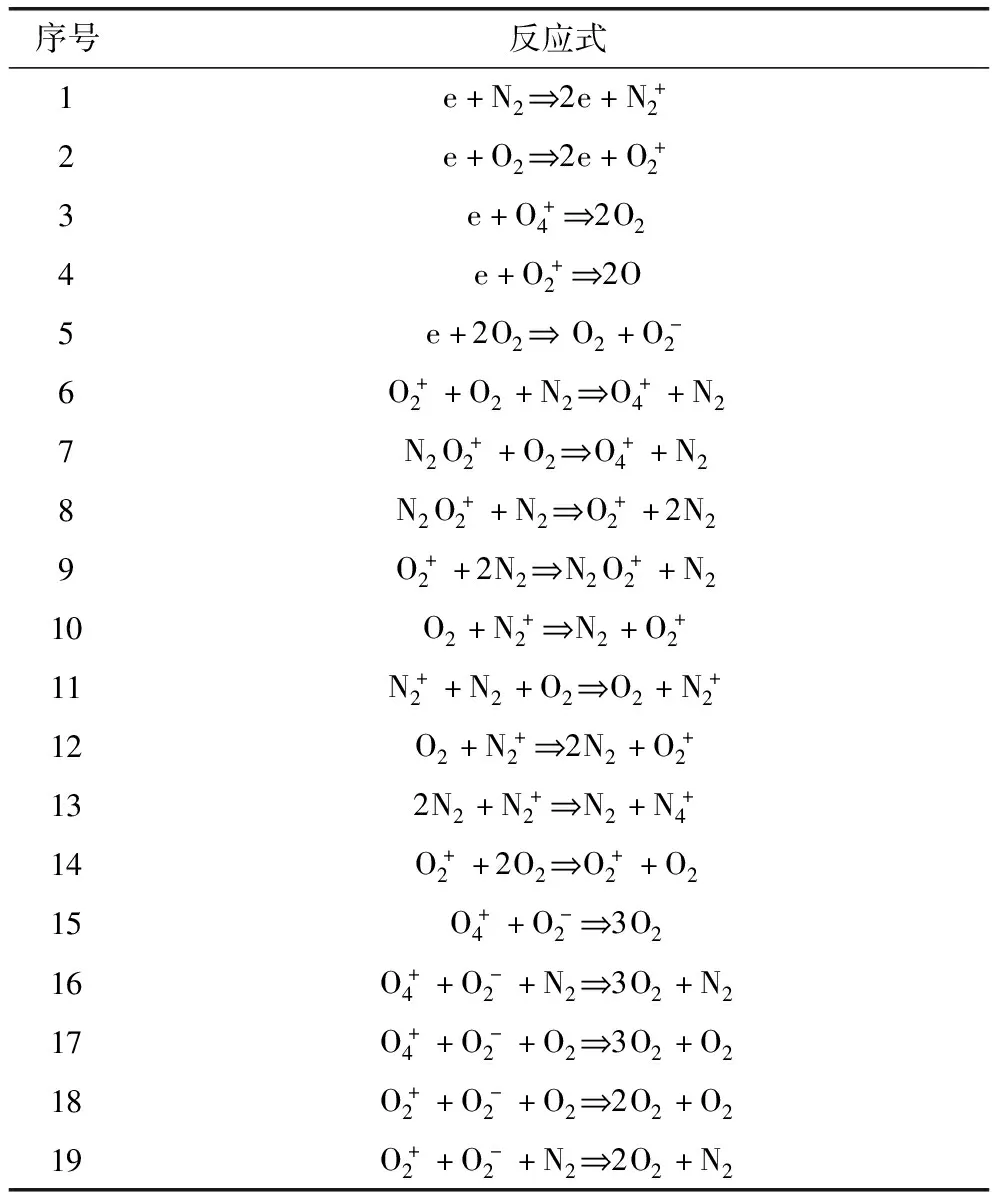
表1 N2-O2等离子体化学反应式

2.3 边界条件

纳米尖阵列模型如图2所示。其中纳米尖端间距为s；V0=300 V；电阻R=1 kΩ；电容C=1 pF；底电极半径L=150 um。由于研究环境为常温常压，因此将环境温度和压强分别设置为293.15 K和101.3 kPa。由于主要探究屏蔽效应与发射面积之间的耦合关系，因此将极间距D、尖端长度H和直径d的值固定为较有利于放电的尺度[15，21]，即D=45 um、H=15 um、d=100 nm。

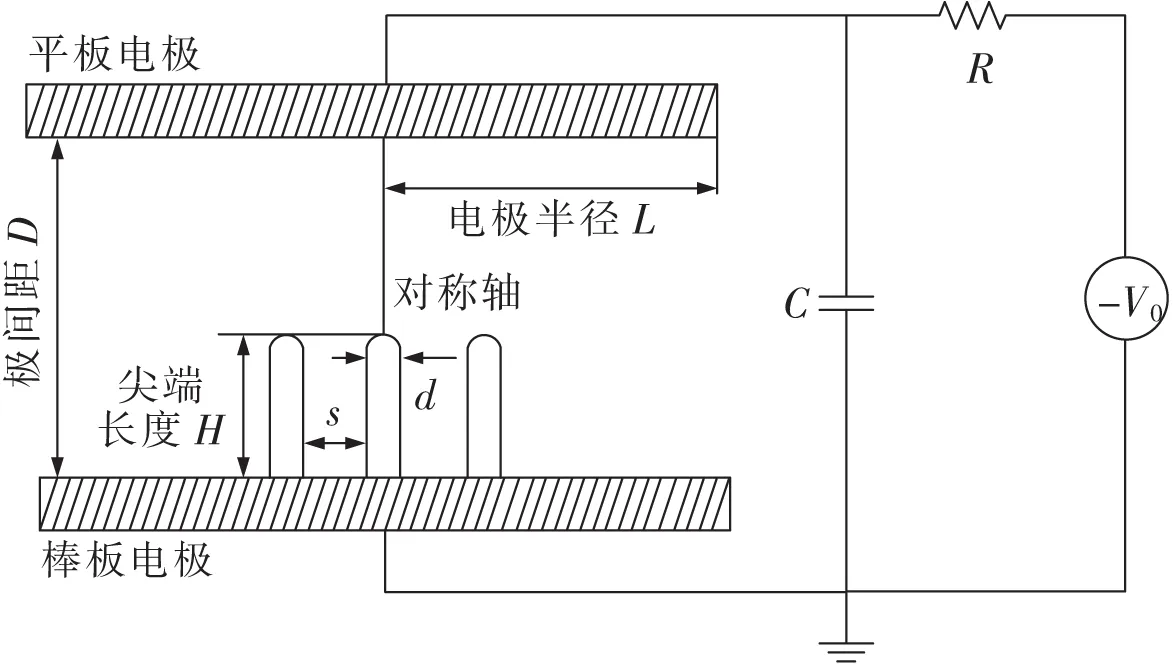
图2 纳米尖阵列模型

正离子在轰击棒板电极时会发生大量二次电子发射的现象，由于二次电子发射主要发生于势垒高度较低的尖端处，因此尖端处的二次发射系数应大于其他部分。二次电子发射系数与平均初始电子能通量的取值范围通常为0.001～0.5 eV和1～5 eV[24]。在仿真中，二次电子发射系数和平均电子能通量取0.05 eV和4 eV，具体的表面反应式及相关数值见表2。

表2 表面反应式

电子通量的边界条件为

Γe=0.5vth,ene-γ∑qiΓi

(8)

(9)

离子通量的边界条件为

Γi=0.5vth,inp+αnpEμi

(10)

(11)

中性粒子的边界条件为

Γn=0.5vth,nnn

(12)

(13)

式中 Γe,Γi,Γn;vth,e,vth,i,vth,n；ne，np，nn分别为电子、离子和中性粒子的密度通量、热速率和密度；μi，mi，qi分别为第i个粒子的迁移率、质量和核电荷数；me，mn分别为电子和中性粒子的质量；kB为Boltzmann常数；Te和T分别为电子温度和环境温度；γ为二次电子发射系数；α为电离系数。

3 计算结果及分析

3.1 屏蔽效应对放电电流的影响

在一定条件下，纳米尖端之间的屏蔽效应是影响气体电离过程的重要因素。电离器件阴极纳米尖端的数量均为3根，旨在通过改变纳米尖端间距的大小，进而观察尖端间距与屏蔽效应之间的关系及其对放电电流的影响。

图3为不同间距纳米尖端的等势线分布，其中图3(a)、3(b)、3(c)的间距s分别为0.07H、0.3H和6.7H。从图2(a)可以看出，由于阴极纳米尖端之间的屏蔽效应，使等势线沿纳米尖端两侧进行扩散，而位于中间的纳米尖端几乎被完全屏蔽。造成这种现象的原因是：当阴极的纳米尖端间距较小时，中间纳米尖端到两侧纳米尖端基本处于同一电势，尖端之间的等势线几乎不弯曲；此时由于纳米尖端附近有着相同的电势，尖端处于同一等势面，纳米尖端之间整体形成了一个类空腔，空腔具有屏蔽外电场的屏蔽效应。因此，位于中间的纳米尖端附近的电场强度要小于位于外侧纳米尖端附近的电场强度。随着纳米尖端间距的增加，屏蔽效应逐渐减小。当尖端间距s=0.3H时，尖端间的等势线已出现下沉，位于中间的纳米尖端逐渐暴露出来。当尖端间距s=6.7H时，各个尖端已经几乎不再相互影响，等势线分布状态接近于尖端本身的独立放电。

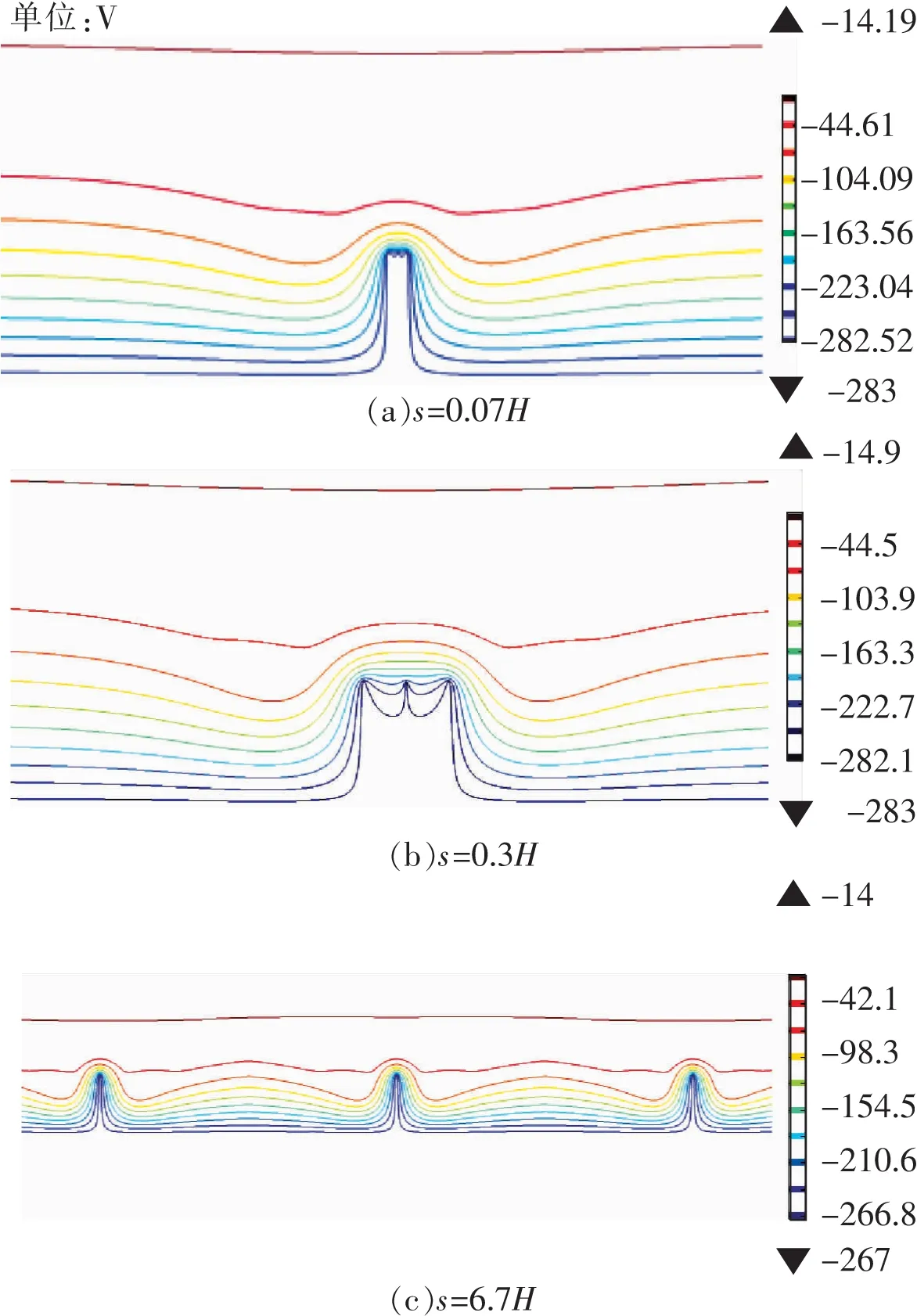
图3 不同间距纳米尖端等势线分布

为了得到尖端间距与屏蔽效应和放电电流之间的关系，将对纳米尖端顶部处的电场强度作为参考进行对比分析。将计算得到的位于中间位置的纳米尖端顶部的电场强度记为局部电场强度EN；在同样条件下，计算得到单根纳米尖端的放电模型，取单根纳米尖端顶部的电场强度记为局部电场强度EO；将纳米尖端之间的屏蔽率η定义为式(14)

(14)

屏蔽率与纳米尖端间距之间的关系如图4所示。从图4可以看出，纳米尖端间的屏蔽效应随尖端间距的增加而减小；当尖端间距s=0.07H时，屏蔽率高达71.6%；而当尖端间距增大到s=6.7H时，屏蔽率则减小到了0.7%，这说明阵列中的纳米尖端的发射效率已经达到了其无屏蔽效应时的99%，发射效率已经非常高；当尖端间距继续增大到s=7.3H时，屏蔽率可以减小到0.5%；因此，在纳米尖端高度H=15 um的情况下，当尖端间距s>6.7H时，可以忽略尖端之间的屏蔽效应。

图4 屏蔽率与放电电流随尖端间距的变化情况

为得到纳米尖端间的屏蔽效应对放电电流的影响，采用有限元法结合边界条件对二维轴对称纳米尖阵列进行了数值模拟。在计算中，保持阴极尖端数量为3根，以此保证纳米阵列发射面积的一致；纳米尖端间距的变化范围为0.07H～7.3H，可以得到电流密度随尖端间距增大的变化情况，从图4可以看出，随着尖端间距的增大，放电电流也随之增大；当尖端间距s=6.7H后，放电电流的增幅较之前有明显减弱。造成这种现象的原因是：起初纳米尖端之间的间距较小，在尖端数量相同的情况下，尖端之间的屏蔽现象较为严重，因此随着尖端间距的增加，尖端的电流密度呈现递增的趋势；而随着尖端间距增加至s=6.7H时，由于屏蔽率已经减小到0.7%，因此,随着尖端间距的增加，电流尽管也在增加，但增幅十分微小，电流增幅的大小逐渐降低。

3.2 尖端屏蔽效应的动态描述

场致电离器件的放电机理主要体现在放电过程中电子的动态过程中。由3.1可知，在纳米尖端间距达到6.3H时，尖端间的屏蔽效应可以忽略不计。为了更清晰地观察到不同间距下纳米尖端动态放电过程的变化，因此将管间距s分别设置为0.3H和6.7H，观察不同屏蔽率η下动态放电过程中的变化。

图5所示为不同间距纳米尖端电子动态分布，其中图5(a)、(b)的间距分别为s=0.3H和s=6.7H。可以看出，两者的放电过程基本一致。随着放电过程的发展，电子首先均整体向阳极推进；之后阴极纳米尖端附近的电子密度逐渐增加，形成了密度较大的电子团；之后电子团逐渐向阳极移动，最终到达阳极；电子团在阳极维持一段时间后又向阴极移动；最终在阴极附近某处保持稳定。

这种放电现象形成的原因是：通电初期，在电容C的作用下，器件阴极的外加电压缓慢上升，此时由于空间内的电场强度和电子能量较小，不易发生碰撞电离，因此主要表现为电子整体向阳极迁移。由于纳米尖端附近的电场强度较大，因此会在相应的轴线上有电场的增强，因此尖端上方的电子会以更快的速度向阳极移动，所以整体的电子密度会呈现波浪状，如图5(a)、(b)中a1、b1所示。随着电压的升高，间隙中的电场强度逐渐增加，纳米尖端附近的场强也随之增加，随着尖端附近场强的增加，大量正离子撞击尖端产生二次电子发射，产生的二次发射电子成为了表1中反应式(1)、(2)的种子电子，因此尖端附近的电子密度增加，如图5(a)、(b)中a2、b2所示。纳米尖端产生的二次发射电子在电场的作用下获得能量，在向阳极运动的过程中与间隙中的气体分子发生碰撞电离，碰撞电离产生的电子又会在电场的作用下获得能量并碰撞其他的气体分子进而引起电子雪崩，电子也因此在间隙中得以增值。当电子团到达阳极时，会与器件表面发生复合而消失。但由于间隙中的碰撞电离仍在继续，间隙中的电子仍在持续产生，且速率不断提高，这使得被复合的电子数小于新产生的电子数，因此电子团在阳极持续了一段时间且密度不断增加，如图5(a)、(b)中a3、b3所示。电离产生的正离子不断向阴极移动，使纳米尖端附近的场加强作用不断增加，因此二次电子发射数量也随之增加，致使尖端附近电子密度不断增加；在阳极附近，由电子附着反应产生的负离子不断累积，使其与阳极之间的场加强作用增强，致使电子在阳极复合的速率加快；在二者的共同作用下，尖端附近的电子密度不断增加，阳极附近的电子密度相对减小，整体表现为电子团向尖端方向移动，如图5(a)、(b)中a4、b4所示。某一时刻，正负离子的产生与消耗达到动态平衡，此时电子团会停留在间隙之间的某个位置，空间电子分布达到稳定的局部自持放电，如图5(a)、(b)中a5、b5所示。这与文献[15]所述情况一致。

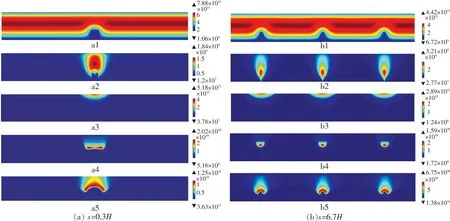
图5 不同间距纳米尖端电子动态分布/(1·m-3)

从图5(a)、(b)可以看出，当尖端间距s=0.3H时，3根纳米尖端的放电过程出现了由屏蔽效应导致的电子团聚合现象，且一直存在于整个动态过程之中；而当纳米尖端间距s=6.7H时，各纳米尖端的动态放电过程基本相互独立，屏蔽效应基本消失，这与3.1所述的结论相符。本节通过对纳米尖端动态放电过程的观察，进一步印证了3.1的结论，并且对整个微电晕放电机理的动态过程进行了分析。

3.3 尖端屏蔽效应与发射面积的耦合机制

由3.1与3.2可知，在底电极大小确定的情况下，随着纳米尖端间距的不断增大，尖端间的屏蔽效应会逐渐减小，当尖端间距大于等于6.7H时，其屏蔽效应可以忽略不计。虽然随着纳米尖端间距的增大，尖端附近的电场强度增强，屏蔽效应减小，但如果仅增大尖端间距，会使单位面积内纳米尖端的数量减小，即有效发射面积减小，这会导致整体放电强度减弱，最终使放电电流减小[25]。同理，随着尖端间距的减小，虽然使得单位面积内纳米尖端的数量增大，但如果仅增加尖端数量，会使尖端周围的电场强度减小，屏蔽效应增大，导致整体放电强度减弱，最终使放电电流减小。因此将进一步探究不同尖端间距与尖端数量对空间放电的影响，即探究场致电离器件阴极板的最佳尖端间距，使其在减小屏蔽效应的同时，尽量增大纳米尖端的数量，进而提高电离器件的放电电流。

为了探究屏蔽效应与发射面积之间的耦合关系，在底电极半径L=60 um的情况下，对不同尖端间距及其对应的尖端数量进行仿真计算，具体的数值见表3。进而探究当电离器件底电极大小一定的情况下，纳米尖端间屏蔽效应与发射面积之间的耦合关系对放电电流的影响。

表3 不同尖端间距下尖端数量与屏蔽率的对应关系

图6为屏蔽效应与发射面积耦合对放电电流的影响。可以看出，随着尖端间距的不断增大，放电电流呈现出先增大后减小的趋势，当尖端间距s=0.9H时，放电电流达到最大。造成此现象的原因是：当s<0.9H时，随着管间距的增大，虽然极板上的纳米尖端数量有所减小，但尖端间的屏蔽效应也随之减小，表现出因尖端间距增大导致屏蔽率减小对放电强度的增强作用大于因尖端数量减少对放电强度的减弱作用，从而致使放电强度增大，放电电流增强。即当管间距从0.6H增加至0.9H时，纳米尖端数量由13减小至9，从而致使放电电流由5.6 mA增大到6.3 mA。当尖端间距s=0.9H时，尖端间距与尖端数量间的耦合关系对空间放电的促进作用达到最佳，放电电流达到最大。当s>0.9H时，再次增大尖端间距，虽然纳米尖端周围的电场强度会进一步增强，但其增强作用不足以弥补由于发射极数量减小致使二次电子发射面积和总场增强区域减小，从而使得放电电流减小。

从图6可以看出，当纳米尖端间距s=0.9H时，该尺度下场致电离器件的放电强度最强，输出电流最大，屏蔽效应与发射面积之间的耦合关系达到最佳。

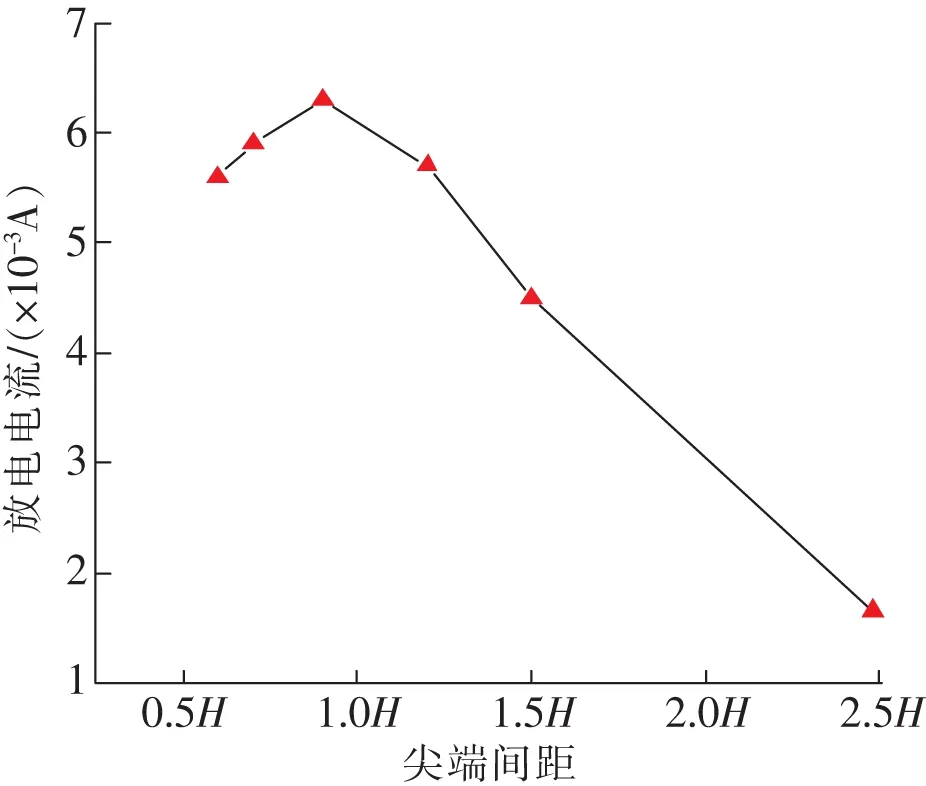
图6 屏蔽效应与发射面积耦合对放电电流的影响

4 结 论

1)在所述尺度下的纳米尖阵列中，随着纳米尖端间距的增加，尖端间的屏蔽效应会逐渐减弱，当尖端间距增加到s=6.7H时，纳米尖端之间的屏蔽效率μ减弱至0.7%，且放电电流因屏蔽效应的减弱而逐渐增加。

2)在所述尺度下的纳米尖阵列中，将纳米尖端间距设置为s=6.7H，可以观察到，各尖端的电子密度动态过程基本一致，且电子团之间的聚合现象几乎没有；因此，在纳米尖端间距s=6.7H时，尖端之间的屏蔽效应可以忽略不计。

3)经仿真验证，通过探究最有利于放电的尖端间距，即最佳的纳米尖阵列形貌，得出在所述的尺度下，当尖端间距s=0.9H时，常压微电晕放电的放电电流最大，屏蔽效应与发射面积之间的耦合关系达到最佳。