基于复阻尼模型的混合结构近似解耦法

赵志明 杨 红，2，* 孙攀旭 刘庆林

（1.重庆大学土木工程学院，重庆400045；2.重庆大学山地城镇建设与新技术教育部重点实验室，重庆400045；3.深圳信息职业技术学院交通与环境学院，深圳518172）

0 引 言

钢-混凝土混合结构能够综合利用钢结构和混凝土的优点，在现代建筑中已得到广泛应用［1-3］。这类结构由阻尼性能存在差异的材料组成，因此属于非比例阻尼结构，其阻尼矩阵不再满足对振型向量的正交性，无法直接利用常规的实模态叠加法进行结构的动力响应分析［4-5］。

为解决该问题，部分学者将非比例阻尼结构体系近似为比例阻尼结构体系，采用整体Rayleigh 阻尼模型计算混合结构的动力响应。黄维等［6-7］基于随机地震动激励下位移响应误差最小原则建议了最佳等效阻尼比公式，根据Rayleigh 阻尼模型来计算竖向混合结构的动力响应；李小珍等［8］分析了结构阻尼比和参考频率选取对耦合系统动力响应的影响规律，并基于Rayleigh 阻尼模型的带通滤波特征提出了车-轨-桥混合动力系统中Rayleigh 阻尼参数的统一取值方法；陈旭等［9］提出选取控制结构反应的子结构周期来确定Rayleigh 阻尼矩阵。与上述基于整体Rayleigh 阻尼模型的近似求解法相比，采用分块Rayleigh 阻尼模型的求解思路能更好地反映各部分的耗能特性［10］。Clough 等［11］、Huang 等［12］基于Rayleigh 阻尼模型构建混合结构的子结构阻尼矩阵，将各子结构的比例阻尼矩阵组装成非比例阻尼矩阵，通过数值积分法来进行混合结构动力响应分析，但计算量较大。为提高计算效率，汤燕波［13］基于分块Rayleigh 阻尼模型来构造混合结构的阻尼矩阵，采用忽略阻尼矩阵非对角项的近似解耦法。

上述两类方法均建立在Rayleigh 阻尼模型基础上，其最大的不足是形成阻尼矩阵时会受振型组合的影响，带有一定的主观性，存在计算结果不唯一、合理性不易被确定的缺点。而基于复阻尼模型得到的阻尼矩阵仅依赖于材料损耗因子，阻尼矩阵可以唯一确定，因此部分学者采用复阻尼模型来进行非比例阻尼结构体系的动力响应分析。黄本才［14］、任红伟［15］、黄维［16］等依据复阻尼模型的时域运动方程，将非比例阻尼体系的特征值等效为比例阻尼体系的特征值，得到等效振型阻尼比，以实现非比例阻尼体系动力响应的计算，但由于忽略了阻尼矩阵实部和虚部的耦合作用，其计算精度难以保证。朱镜清等［17］根据复化对偶原则提出了基于复阻尼模型的实模态以及复模态叠加法以求解多自由度系统的动力响应；刘庆林等［18］采用基于复阻尼假定的复模态叠加法，直接在物理空间求解，计算结果唯一。但上述方法均需要计算结构的复振型向量，其计算过程较为复杂，不适于在工程结构计算中推广使用。

针对混合结构的动力响应计算，本文依据近似解耦法，提出了基于复阻尼模型的实模态叠加法。与基于Rayleigh 阻尼模型的实模态叠加法相比，本文提出的方法具有计算结果唯一、合理性易判定的优点；相比基于复阻尼模型的复模态叠加法，本文提出的方法计算简便，更适合实际工程的结构计算。

1 基于复阻尼模型的近似解耦法

地震作用下基于复阻尼模型的多自由度体系时域运动方程为

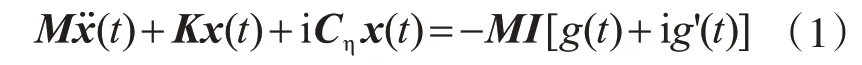
式中，M 为结构的质量矩阵；K 为结构的刚度矩阵；Cη为结构的阻尼矩阵；g(t)为地震加速度；I 为与地震动输入有关向量；与g(t)方向相同的元素为1，其他为零；i为虚数单位，即i= -1。

假定体系是由不同阻尼特性材料组成，可得到结构的阻尼矩阵为

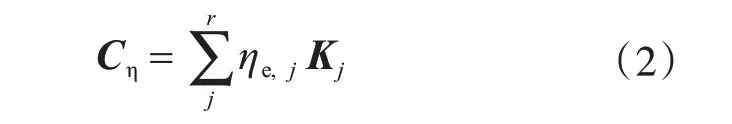
式中：r 为材料种类的个数；ηe，j为第j 种材料的损耗因子；Kj为第j种材料对应的刚度矩阵。

方程式（1）对应的无阻尼振型向量矩阵为

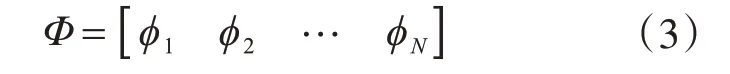
采用无阻尼振型向量可对质量矩阵和刚度矩阵进行正交化

对于小阻尼比情况下，忽略非对角元素的影响，采用近似解耦的方法，仅保留对角项，即

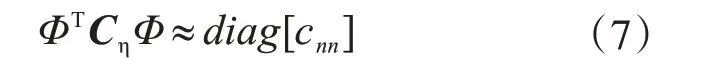
位移向量由振型向量线性表出

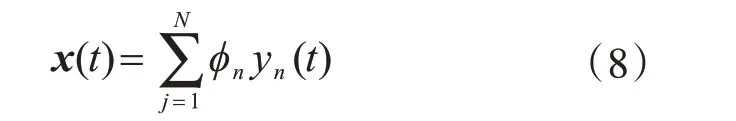
方程式（1）则可转化为

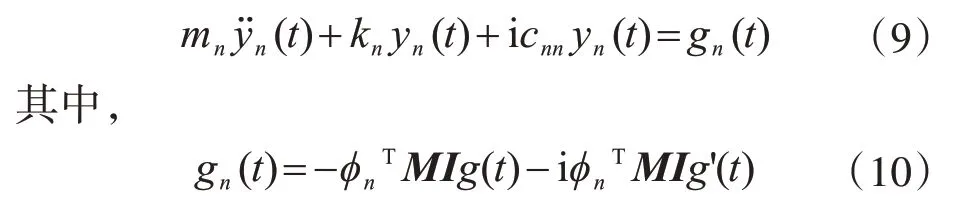
地震加速度采用三角级数展开

式中，常数项需利用静力条件进一步确定，在恒载作用下方程式（1）表示为

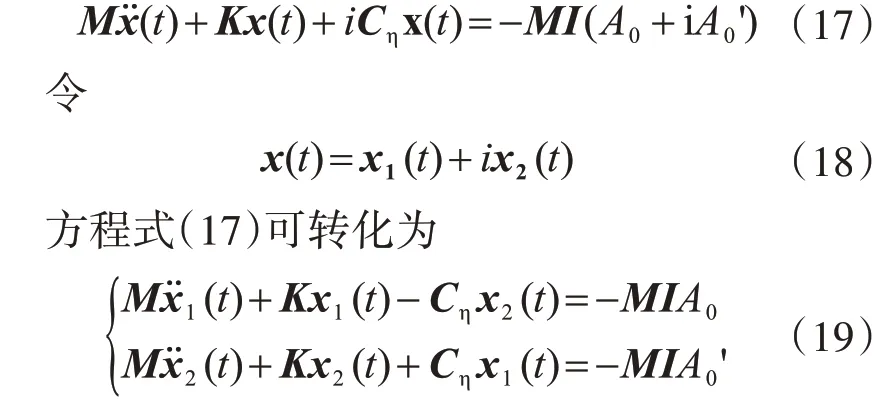
在恒载作用下，响应可直接利用受力平衡得到，即

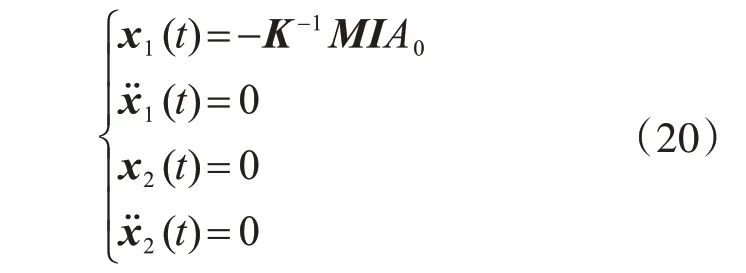
将式（20）代入方程式（19），得

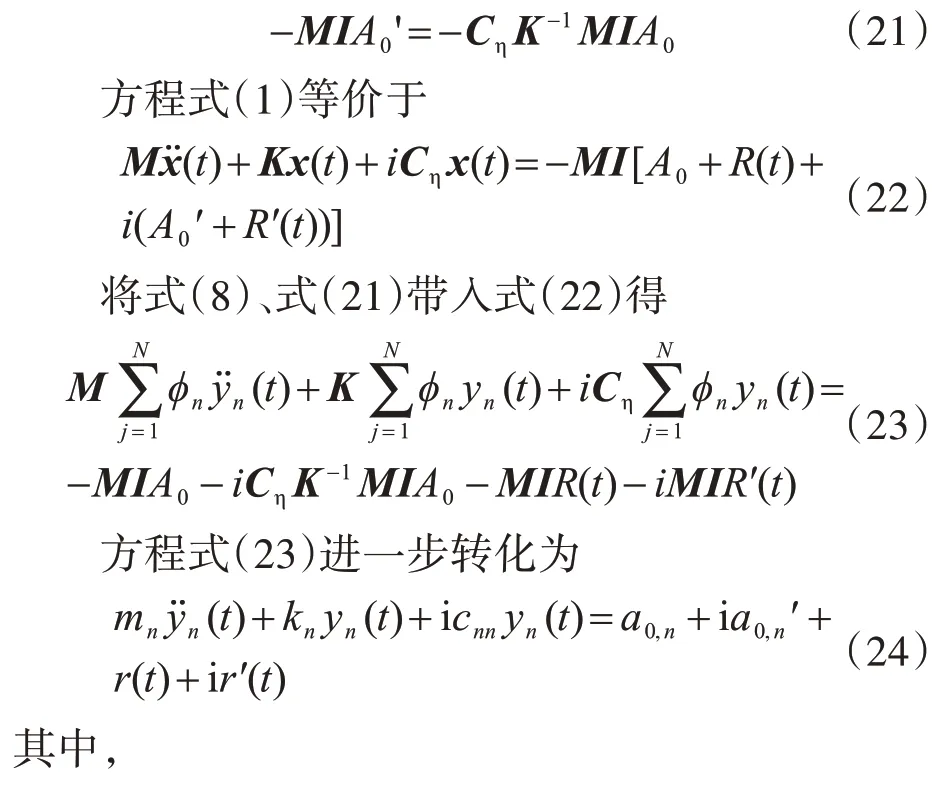
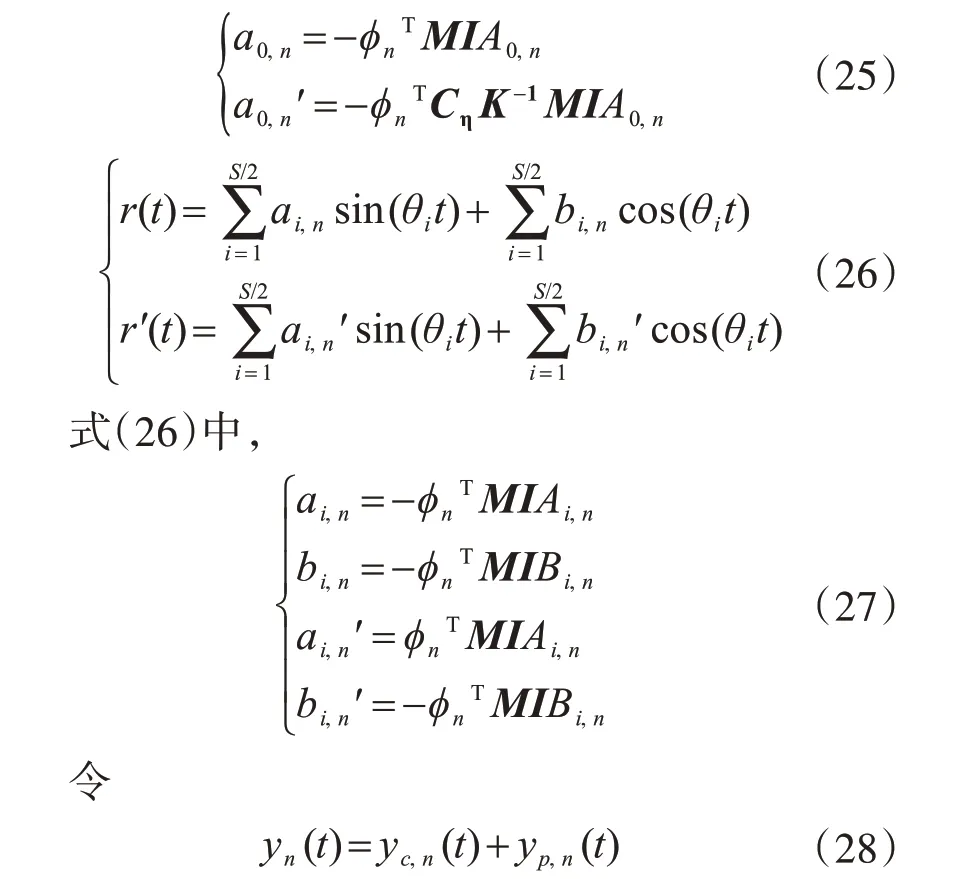
式中，yc，n(t)为方程式（24）对应的齐次方程通解；yp，n(t)为方程式（24）对应的非齐次方程特解。

方程式（9）对应的齐次方程为

依据式（32），可知方程式（33）的通解实部为

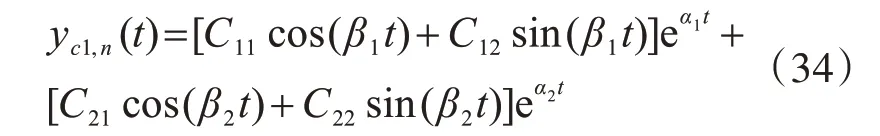
式（34）第二项为发散项，根据物理意义进行剔除，式（34）转化为

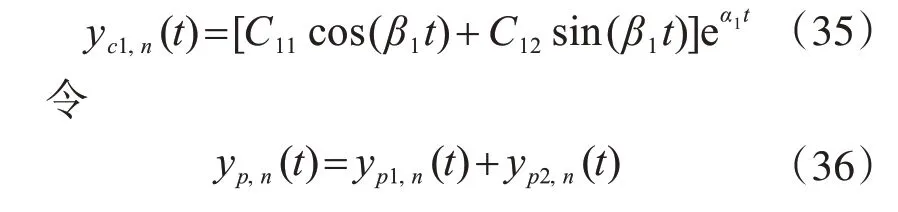
其中，yp1，n(t)为方程式（24）中(a0，n+ia0，n′)对应的特解，yp2，n(t)为方程式（24）中(r(t)+ir′(t))对应的特解。

对于方程

由式（51）可计算出yn(t0)和ẏn(t0)，进而完成基于复阻尼模型的混合结构模态叠加法。

2 算例分析

分别构建2 自由度的竖向混合结构模型A 和9 自由度的竖向混合结构模型B，如图1 所示，结构上部皆选用钢结构，其阻尼比为0.02，对应的损耗因子为0.04［18］；结构下部均选用钢筋混凝土结构，阻尼比为0.05，对应的损耗因子为0.10［18］。模型A和B的自振频率如表1所示。

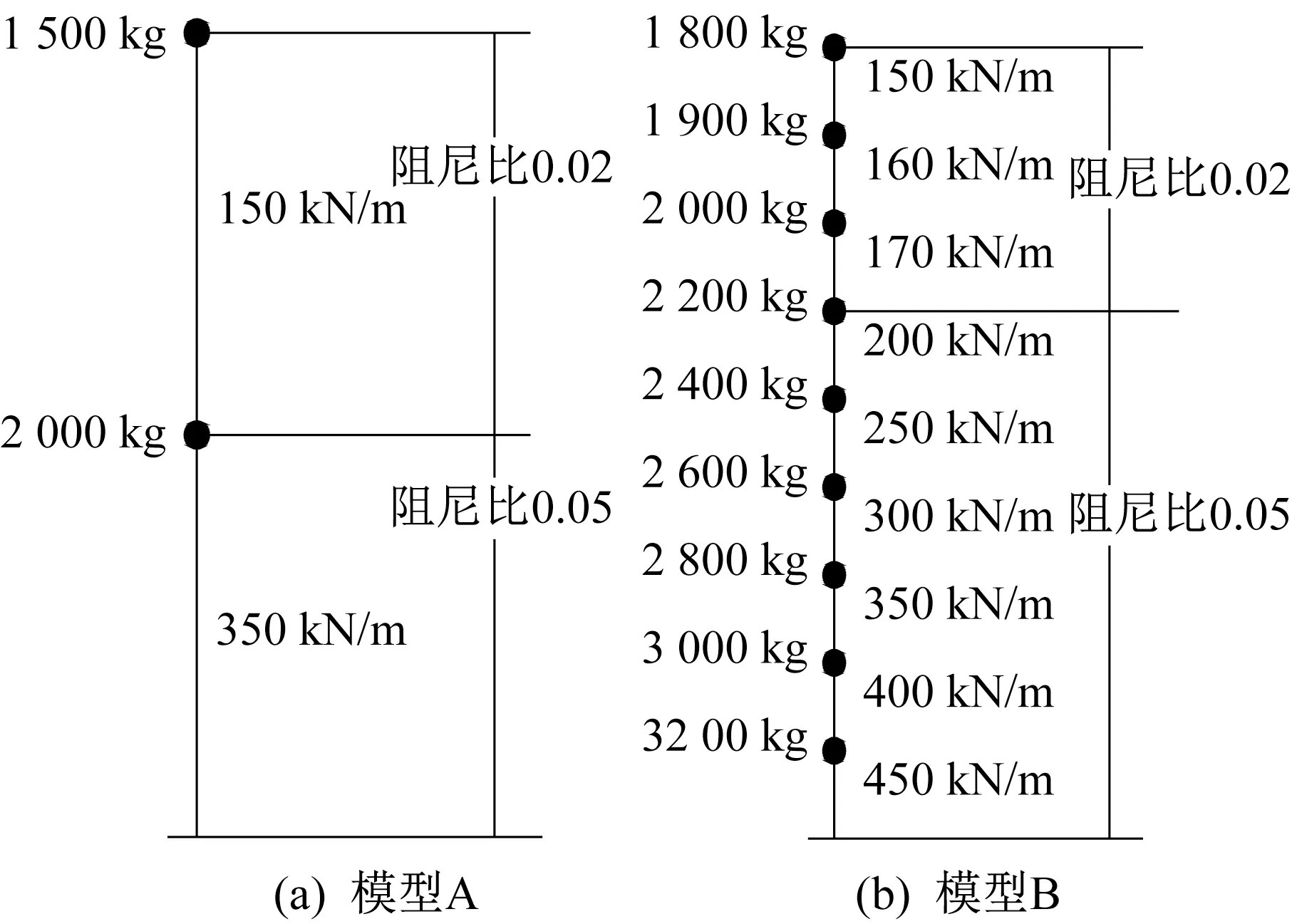
图1模型参数Fig.1 Model parameter

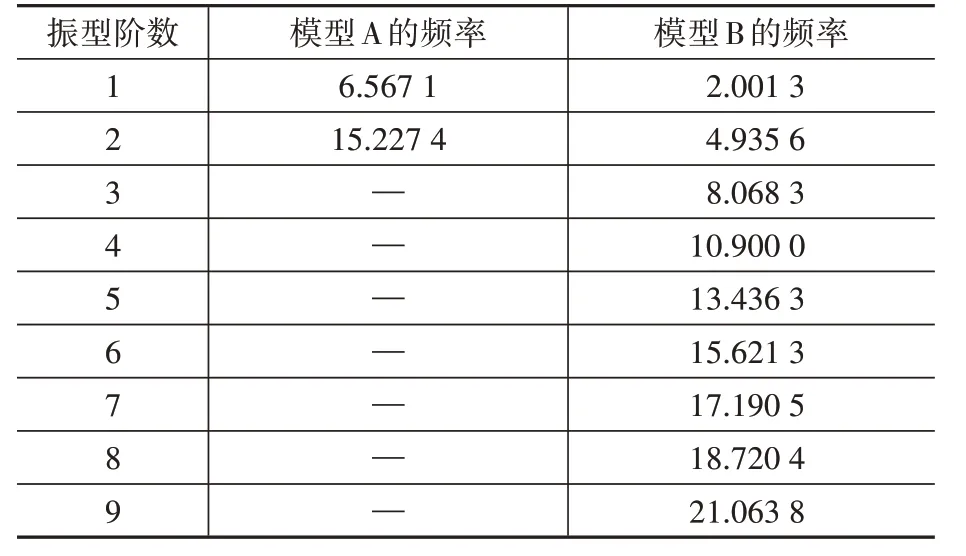
表1 模型A和B的自振频率Table 1 Dynamic characteristics of ModelAand B rad·s-1

图2 El Centro 波作用下模型A的顶层响应Fig.2 Top response of Model A under El Centro wave

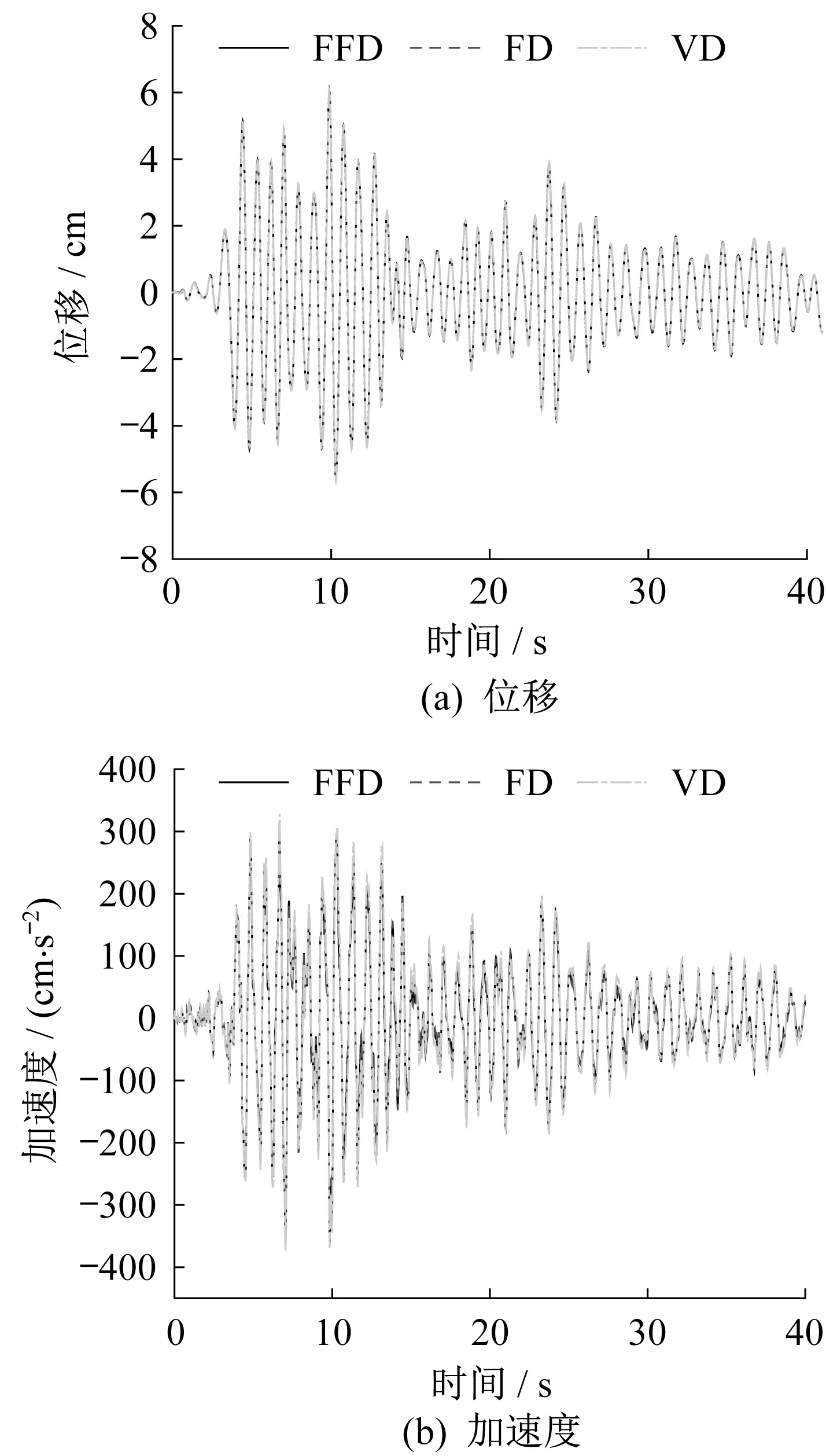
图3 Taft波作用下模型A的顶层响应Fig.3 Top response of Model A under Taft wave

分别采用基于复阻尼模型的频域法（FFD）、本文方法（FD）和基于黏性阻尼模型的近似解耦法（VD）计算模型A 的位移响应和加速度响应，结果如图2、图3 所示，其中基于复阻尼模型的频域法（图中FFD）可视为精确解［19］。对于混合结构，采用黏性阻尼模型进行计算时，可采用分块Rayleigh 阻尼矩阵法构造阻尼矩阵。模型A 为二自由度体系，采用分块Rayleigh 阻尼矩阵法时直接选择第一阶振型和第二阶振型构造阻尼矩阵，进而实现基于黏性阻尼模型的近似解耦法。模型A 的计算结果对比表明，FD 和FFD 的位移时程和加速度时程近似相等（图2和图3），峰值位移和峰值加速度的相对误差在5%以内（表2 和表3），因此小阻尼比情况下，采用基于复阻尼模型的近似解耦法可满足计算精度；FFD和VD的位移时程和加速度时程近似相等（图2和图3），峰值位移和峰值加速度的相对误差在5%以内（表2 和表3），因此小阻尼比情况下，对于二自由度体系，基于复阻尼模型的近似解耦法和基于黏性阻尼模型的近似解耦法计算结果近似相等。

与模型A 相同，仍然分别采用FFD、FD 和VD计算模型B 的位移响应和加速度响应，所得结果如图4、图5 和图6 所示。对比计算结果表明，FD和FFD 的位移时程和加速度时程近似相等（图4-图6），峰值位移和峰值加速度的相对误差在5%以内（表4-表6），这进一步证明了基于复阻尼模型近似解耦法的正确性。

由于模型B 为九自由度体系，采用分块Rayleigh 阻尼矩阵法构造阻尼矩阵时需要考虑振型组合问题，这也是实际工程结构均会面临的问题。为尽量全面、合理地考虑实际工程应用可能选择的做法，本文分别采用基于第一阶振型和第二阶振型的黏性阻尼模型近似解耦法（VD1）、基于第一阶振型和外激励卓越频率接近振型的黏性阻尼模型近似解耦法（VD2）计算了模型B 的动力响应。

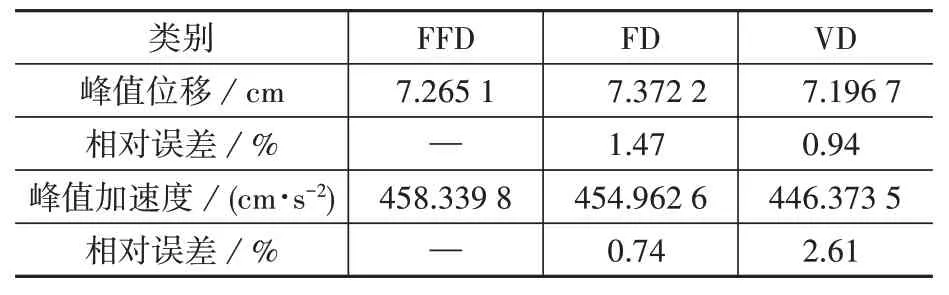
表2 El Centro 波作用下模型A的顶层响应Table 2 Top response of Model A under El Centro wave

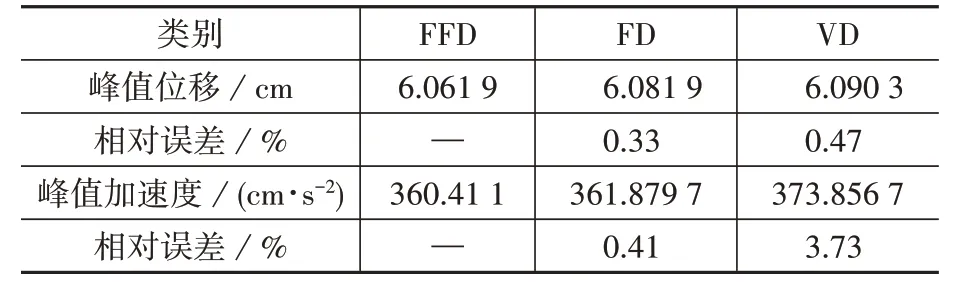
表3 Taft波作用下模型A的顶层响应Table 3 Top response of Model A under Taft wave

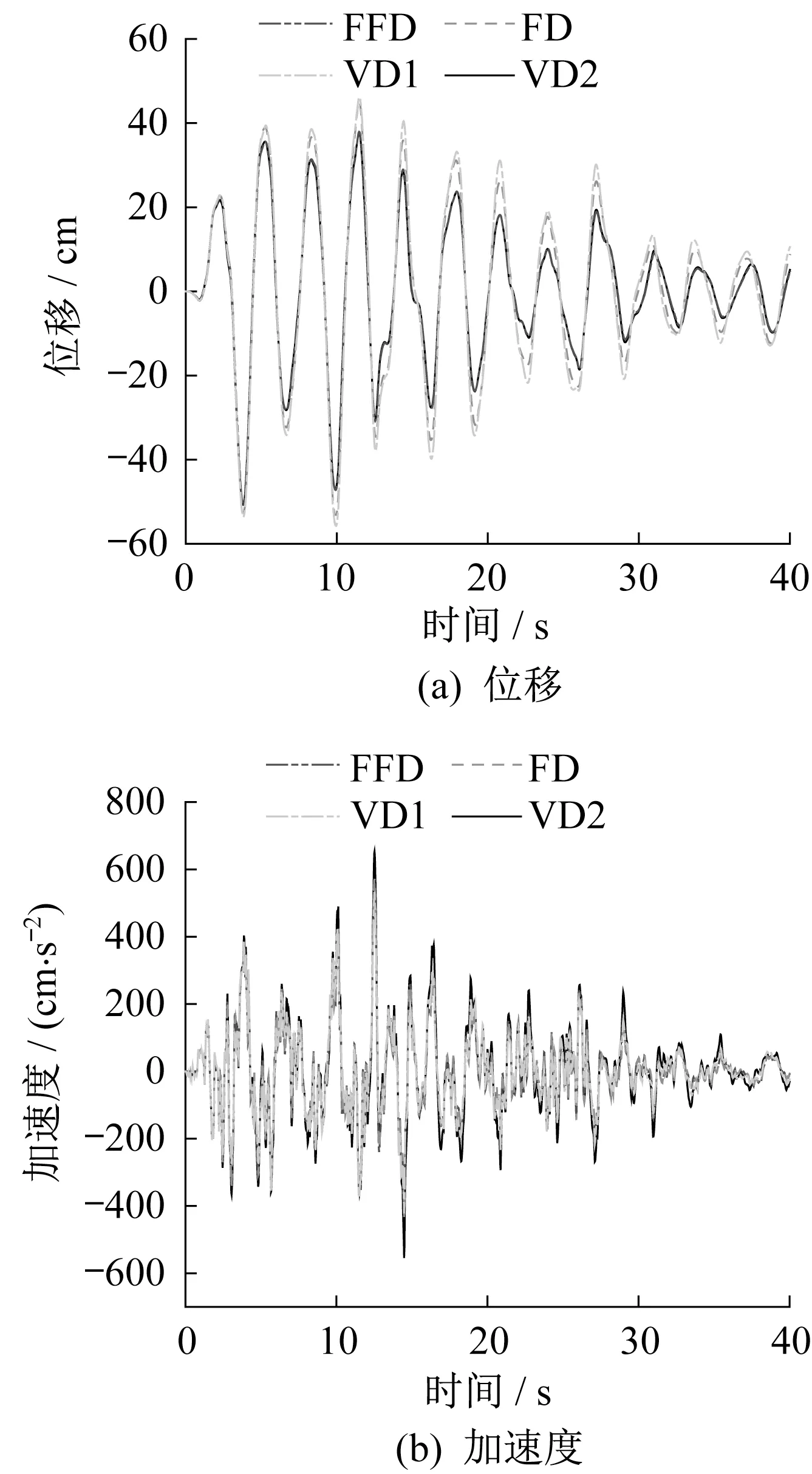
图4 El Centro 波作用下模型B的顶层响应Fig.4 Top response of Model B under El Centro wave

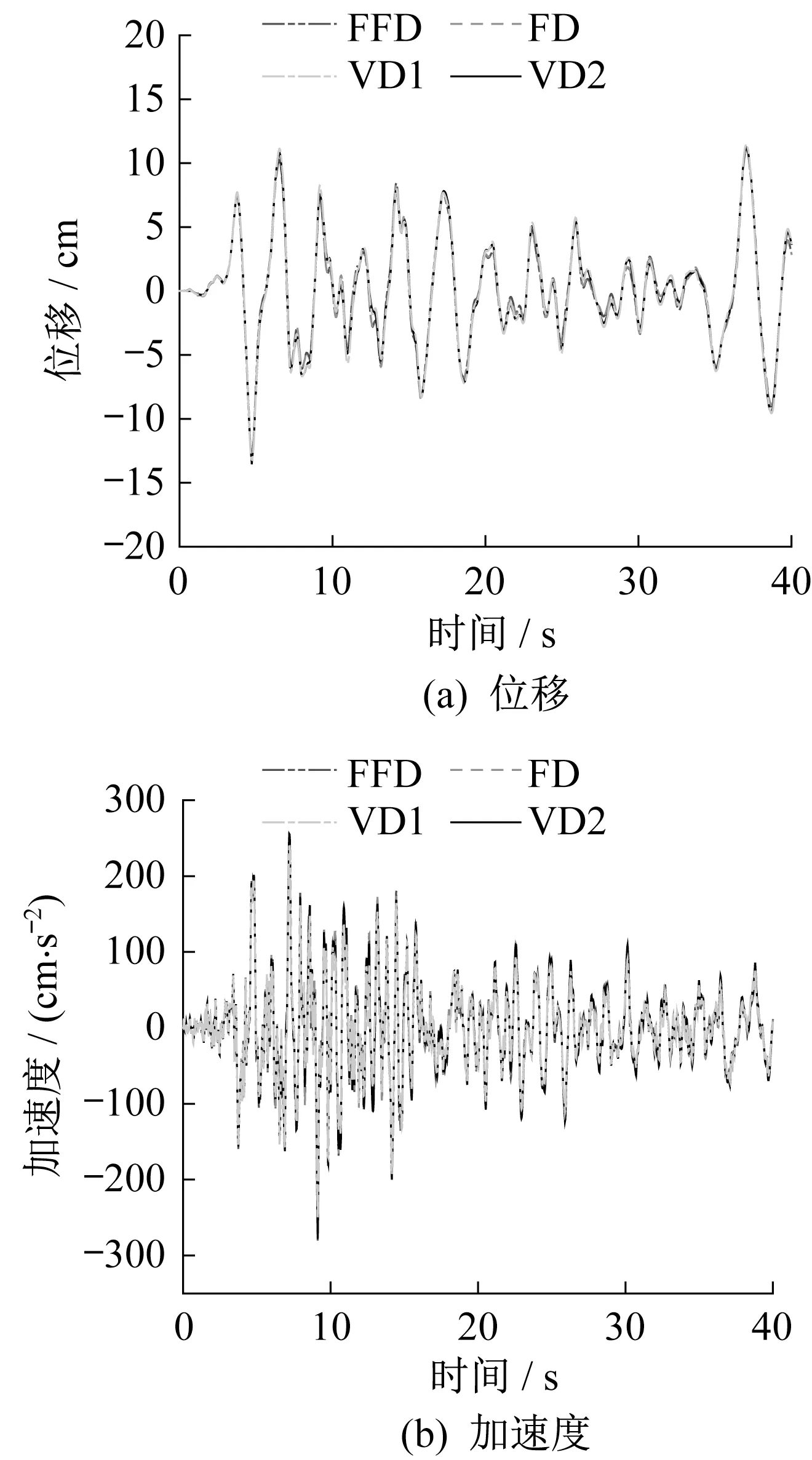
图5 Taft波作用下模型B的顶层响应Fig.5 Top response of Model B under Taft wave

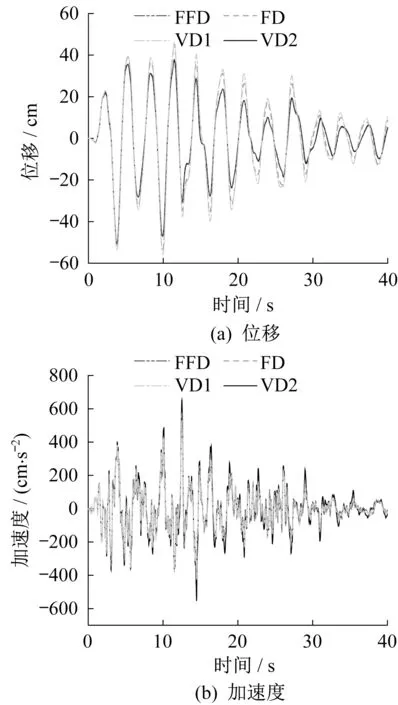
图6 天津波作用下模型B的顶层响应Fig.6 Top response of Model B under Tianjin wave

El Centro 波作用下，FFD 和VD1 的位移时程和加速度时程差异较小，FFD 和VD2 的位移时程和加速度时程差异较大（图4），FFD 和VD1 的峰值位移相对误差为4.71%，FFD 和VD1 的峰值加速度相对误差为5.66%，FFD 和VD2 的峰值位移相对误差为9.91%，FFD 和VD2 的峰值加速度相对误差为15.44%（表4）。

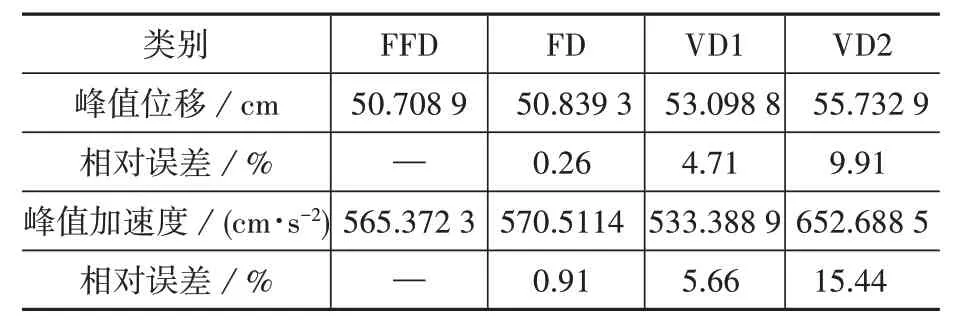
表4 El Centro 波作用下模型B的顶层响应Table 4 Top response of Model B under El Centro wave

Taft 波作用下，FFD 和VD1 的位移时程近似相等，但加速度时程差异较大，FFD和VD2的位移时程和加速度时程近似相等（图5），FFD 和VD1的峰值位移相对误差为4.75%，FFD 和VD1 的峰值加速度相对误差为10.33%，FFD 和VD2 的峰值位移相对误差为2.00%，FFD 和VD2 的峰值加速度相对误差为0.89%（表5）。

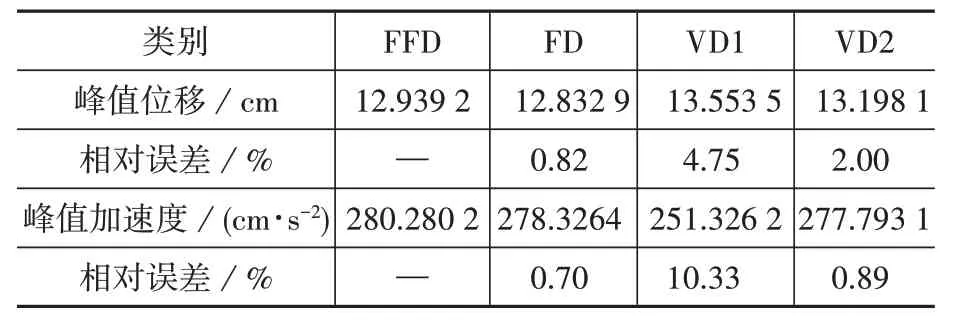
表5 Taft波作用下模型B的顶层响应Table 5 Top response of Model B under Taft wave

天津波作用下，FFD 和VD1 的位移时程和加速度时程近似相等，FFD 和VD2 的位移时程和加速度时程差异较大（图6），FFD 和VD1 的峰值位移相对误差为1.17%，FFD 和VD1 的峰值加速度相对误差为1.86%，FFD 和VD2 的峰值位移相对误差为6.14%，FFD 和VD2 的峰值加速度相对误差为7.82%（表6）。

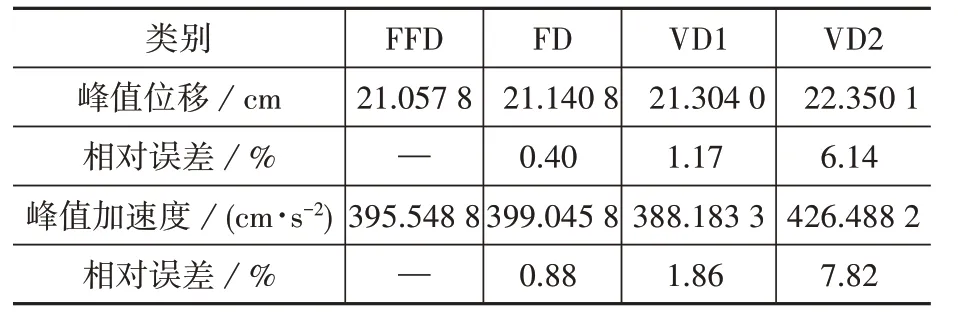
表6 天津波作用下模型B的顶层响应Table 6 Top response of Model B under Tianjin wave

因此，模型B 的计算结果再次证明了黏性阻尼模型在构造阻尼矩阵时总是面临如何合理考虑振型组合的问题，不同的振型组合将造成计算结果的较大差异，基于黏性阻尼模型的近似解耦法计算结果的正确性依赖于振型组合的合理选择，工程常用的振型组合方法（例如VD1 选择第一阶振型和第二阶振型进行组合）也会导致较大的误差（见Taft 波的计算结果），这必然导致该方法的合理性难以判定。与基于黏性阻尼模型的近似解耦法相比，基于复阻尼模型的近似解耦法计算结果唯一，合理性易被判定，适于推广使用。

3 结 论

经理论推导和算例分析，得到以下结论：

（1）依据结构的损耗因子可快速确定结构复阻尼矩阵，在此基础上提出了基于复阻尼模型的近似解耦法，利用三角级数法实现了地震作用下混合结构动力响应的时程计算。

（2）采用分块Rayleigh 阻尼矩阵法构造阻尼矩阵时，对于二自由度体系，基于黏性阻尼模型的近似解耦法计算结果唯一，与基于复阻尼模型的近似解耦法计算结果近似相等；对于一般多自由度体系，基于黏性阻尼模型的近似解耦法计算结果不具有唯一性，其计算结果的正确性依赖于振型组合的合理选择，导致方法的合理性难以判定。

（3）小阻尼情况下，基于复阻尼模型的近似解耦法计算结果可满足计算精度，且计算结果具有唯一性，不涉及振型组合选择问题，合理性易被判定。