整体倾斜对钢筋混凝土框架结构受力性能的影响分析

蒋利学 白 雪 王卓琳 郑乔文 周 源

（上海市建筑科学研究院有限公司上海市工程结构安全重点实验室，上海200032）

0 引 言

我国国家标准《建筑地基基础设计规范》（GB 50007—2011）［1］规定：总高度不超过24 m 的多层建筑的整体倾斜允许值为0.004。但较多既有多层建筑的实际整体倾斜超过这个允许值，尤其在上海等软土地区更为普遍。国家标准《民用建筑可靠性鉴定标准》（GB 50292—2015）［2］规定，当混凝土结构侧移（整体倾斜）超过总高度的1/200时，即认为产生了不适于承载的侧向位移，在构件承载力验算时应考虑侧移的影响。行业标准《危险房屋鉴定标准》（JGJ 125—2016）［3］规定，多层混凝土框架结构因地基变形引起梁、柱出现开裂且房屋整体倾斜率超过0.01，或一、二层房屋整体倾斜率超过0.03，三层及三层以上多层房屋整体倾斜率超过0.02 时，直接判断地基处于危险状态。但是，我国现行标准中均未给出考虑倾斜影响的框架结构构件承载力计算方法。工程实践中对这一问题也未引起足够的重视，除了《危险房屋鉴定标准》（JGJ 125—2016）［3］中规定根据地基危险状态直接评为危险房屋外，在可靠性鉴定中很少考虑整体倾斜对上部结构构件承载力和结构安全性的影响。这可能会给房屋使用造成安全隐患。

文献［4-5］研究了局部倾斜与砌体结构及带填充墙的框架结构构件裂缝损伤的关系，提出了相对倾角、角变形等控制上部结构裂缝损伤的沉降变形（局部倾斜）二阶参数，并给出了这些参数的限值建议。房屋不均匀沉降除了引起上部结构裂缝损伤外，其整体倾斜还会引起上部结构的重力二阶效应，增大构件内力并对构件的承载能力造成不利影响。目前，这方面的研究成果有限，文献［6］研究了倾斜对砌体结构构件受压承载力的影响，并给出了承载力影响系数的计算方法。

本文采用等效侧向荷载法和反弯点法对整体倾斜引起的框架柱、梁弯矩进行分析，建立整体倾斜对框架柱受压承载力和框架梁受弯承载力的影响系数经验公式，并分析整体倾斜对柱、梁承载力的影响程度。研究成果可为既有混凝土框架结构可靠性鉴定提供参考。

1 整体倾斜引起的框架结构二阶效应分析

1.1 现有各种重力二阶效应计算方法分析

结构中的二阶效应指作用在结构上的重力或构件中的轴压力在变形后的结构或构件中引起的附加内力和附加变形。建筑结构的二阶效应包括整体结构侧移二阶效应（P-Δ 效应）和单个受压构件的挠曲二阶效应（P-δ 效应）两部分［7］。前者又称重力二阶效应。我国很多学者对重力二阶效应（P-Δ 效应）进行了研究［8-12］。重力二阶效应的计算方法主要有有限元法和增大系数法两类。

计算重力二阶效应的有限元法有如下四类：

（1）“考虑材料非线性和几何非线性的结构有限元分析法”，这是最完整、最精确的一种有限元方法，它能将P-Δ 效应和P-δ 效应一并进行计算，但需要进行大量迭代计算且十分耗时，故实际工程中很少采用［8］。

（2）“基于等效水平力的有限元法”［9］，其因P-Δ效应产生的等效附加楼层剪力为［10］

式中，Vi为P-Δ 效应在第i 层产生的楼层等效附加剪力；∑Gi为第i 层以上全部重力荷载；ui和ui-1分别为第i 层和第i-1 层楼层标高位置的水平位移，hi为第i层层高。

楼层等效附加剪力与原有剪力叠加后重新计算楼层水平位移，直至前后两次计算的楼层水平位移基本相等。因此基于等效水平力的弹性有限元法需要进行迭代计算［10］。

（3）“基于等效几何刚度的有限元法”［9］（有的软件称之为“负刚度法”或“虚柱法”），这种方法无须迭代计算，很多计算机软件采用这种方法［8］。

（4）“基于折减抗弯刚度的有限元法”，美国《混凝土结构设计规范》（ACI 318—99）采用这种方法，并且给出了钢筋混凝土构件弹性抗弯刚度折减系数的取值建议：梁取0.35，柱取0.7，未开裂剪力墙取0.7，已开裂剪力墙取0.35。我国《混凝土结构设计规范》（GB 50010—2002）也曾引入这种方法，但建议的构件弹性抗弯刚度折减系数与美国规范有所不同：梁取0.4，柱取0.6，对未开裂的剪力墙和核心筒壁取0.7，对已开裂的剪力墙和核心筒壁取0.45［10］。

上述四种有限元法中，除第一种为非线性方法外，其余三种均为通过简化方法考虑非线性影响的弹性有限元法；前两种方法需要进行迭代计算，而后两种方法无须进行迭代计算。

增大系数法将不考虑重力二阶效应的弹性分析得到的内力和位移分别乘以一个增大系数，有“层增大系数法”和“整体增大系数法”两种，前者适用于以剪切变形为主的框架结构，后者适用于以弯剪变形为主的剪力墙结构、框架-剪力墙结构和筒体结构。在计算位移增大系数时，各构件均采用弹性刚度，而在计算内力增大系数时，各构件采用弹性折减刚度。现行国家标准《混凝土结构设计规范》（GB 50010—2010）［7］和行业标准《高层建筑混凝土结构技术规程》（JGJ 3—2010）［13］均有这两类增大系数法的规定，所不同的是：在计算内力增大系数时，前者对不同构件分别采用不用的刚度折减系数（取值与GB 50010—2002 相同），而后者对不同构件采用了统一的刚度折减系数0.5。

除了上述两类方法外，过去还有计算偏心受压构件的η-l0法，这种方法通过偏心距增大系数η考虑构件挠曲二阶效应的影响，而通过计算长度l0考虑有侧移框架的重力二阶效应影响。这种方法在《混凝土结构设计规范》（GB 50010—2002）［7］及其以前版本中有采用。

重庆大学白绍良教授团队对包含P-Δ 效应和P-δ 效应在内的混凝土结构二阶效应进行了大量梳理和研究［8，11-12］，得到的基本结论有：①20 世纪各国规范中混凝土结构二阶效应的计算方法基本上属于η-l0法，这种方法将P-Δ 效应和P-δ 效应混合考虑，是计算手段较传统时代的产物，计算方法比较粗糙，在当今结构计算软件比较普及的情况下宜予弃用；②P-Δ 效应和P-δ效应两类不同二阶效应应予分开计算；③P-Δ 效应只对引起结构侧移的弯矩（主要是水平作用引起的弯矩）有增大作用，而对不引起结构侧移的弯矩（主要是竖向荷载引起的弯矩）没有增大作用；④P-δ 效应对柱端截面的弯矩没有放大作用，而只对柱中部截面弯矩有放大作用，对于一般框架柱，考虑端截面偏心距调节系数Cm（η-l0法改用Cmηns法）后，柱中部截面的弯矩一般不会超过端截面弯矩（两端截面弯矩的较大者），故除了长细比很大、轴压力很大、两端弯矩同号且较接近的框架柱外，一般框架柱在考虑P-Δ 效应影响后，无须同时考虑P-δ 效应的影响。

现行国家标准《混凝土结构设计规范》（GB 50010—2010）［7］根据白绍良教授团队的研究成果，对整体结构P-Δ效应和框架柱的P-δ效应计算方法进行了重大修订，相较于GB 50010—2002 及其更早版本有实质性的改进和完善：对于P-Δ效应的计算，除了有限元法外，还以附录B的形式提出了近似计算方法——增大系数法（包括计算框架结构的层增大系数法和计算剪力墙结构、框架-剪力墙结构和筒体结构的整体增大系数法）；弯矩增大系数不是“统乘”所有弯矩，而只是乘以引起结构侧移的弯矩（主要是水平作用引起的弯矩）；计算弯矩增大系数时，应根据构件类别考虑不同的弯曲刚度折减系数；只有极少数框架柱尚需同时考虑P-δ 效应的影响，并给出了明确的判断条件；改用Cmηns法计算P-δ效应对偏心受压构件的影响。

1.2 用等效侧向荷载法分析整体倾斜引起的框架结构二阶效应

上述混凝土结构重力二阶效应分析均针对结构设计阶段侧向荷载作用的情况，本文研究整体倾斜对既有钢筋混凝土框架结构受力性能的影响，两者侧向位移的性质不同：前者的侧向位移是计算预测值，重力二阶效应对这个侧向位移计算预测值有影响，故采用基于等效水平力的弹性有限元法时需通过迭代计算确定；后者的整体倾斜是地基不均匀沉降引起的结构侧移实测值，分析时是客观存在的，如沉降已稳定则其倾斜率是固定不变的。因此，后者的计算分析更加方便。基于此，本文采用等效侧向荷载法分析整体倾斜引起的框架结构二阶效应：地基不均匀沉降引起的上部结构整体倾斜，对上部结构各楼层、各竖向构件的倾斜率γ 均相等且已知。如图1 所示，以倾斜的竖向串联悬臂杆作为多层结构计算模型，其重力荷载Gi产生的侧向荷载分量为γGi，竖向荷载分量仍接近Gi，则整体倾斜的附加作用效应相当于各层作用一个大小为γGi的侧向荷载引起的效应，故对第i层产生的层剪力为Vi=ΣγGi。

用式（1）计算整体倾斜引起的重力二阶效应时，由于（ui-ui-1）/hi=γ，故也可得到Vi=ΣγGi，其对应的各层等效水平力为γGi。可见，本文提出“等效侧向荷载法”与式（1）代表的“基于等效水平力的有限元法”本质上是完全一致的，但由于整体倾斜引起的水平侧移（倾斜率）是已知的，故可省去迭代求解水平侧移的过程，直接采用等效侧向荷载计算整体倾斜对框架结构梁、柱产生的内力，用常用结构分析软件可方便地进行分析。

为了进一步掌握整体倾斜对框架结构梁、柱承载能力的影响规律及影响程度，本文在第2 节、第3 节先采用反弯点法［14］分析整体倾斜对多层框架柱、梁产生的附加弯矩，然后再分析附加弯矩对梁柱承载能力的影响。

图1 分析整体倾斜效应的等效侧向荷载法Fig.1 Equivalent lateral load method of overall inclination analysis

2 倾斜对钢筋混凝土框架柱受压承载力的影响分析

2.1 相对偏心距对受压承载力的影响分析

按文献［7］，当不考虑P-δ效应时，偏心受压柱的承载力实质上是端部截面的承载力。对对称配筋的框架柱，设柱截面为A，弯矩作用方向的全部纵筋面积为As，混凝土抗压强度设计值为fc，纵筋的强度设计值为fy，柱截面高度为h，柱的轴向压力设计值为N，柱端截面弯矩设计值（取上下两个截面中的较大值）为M，则相应短柱的轴压承载力为Nu，0=Afc+Asfy（这里为简化计算，不考虑另一方向纵筋对短柱轴压承载力的贡献）。定义弯矩作用方向钢筋对短柱轴压承载力的贡献率为ξs=Asfy/Nu，0，则影响偏心受压柱承载力的主要参数是ξs和相对偏心距e0/h（其中，e0=M/N 为柱端截面的初始偏心距）。定义柱的相对受压承载力系数为φN=Nu/Nu，0。根据现行《混凝土结构设计规范》（GB 50010—2010）［7］，对ξs=0.16、0.25、0.32、0.39 四种不同工况的柱截面进行承载力验算，得到相对偏心距对柱受压承载力的影响曲线，见图2。按照文献［7］，长柱的轴心受压承载力为0.9φNu（其中φ 为轴心受压长柱的稳定系数），假定偏心受压柱的最大轴压力不能超过对应轴心受压柱的受压承载力，则φN的最大值不会超过0.9。图2 中，当φN较大时的间隔为0.05，φN较小时的间隔为0.02。可见，相对偏心距e0/h 对相对受压承载力系数φN的影响体现出明显的非线性性质：当φN较大时受e0/h 的影响较敏感（图中曲线较陡），当φN较小时受e0/h 的影响较不敏感（图中曲线较平缓）；φN较大时，受ξs影响较小（图中几条曲线基本重叠），φN较小时，受ξs影响较大（图中几条曲线分化明显，ξs越大，φN减小速率越小）。

图2 相对偏心距对柱受压承载力的影响Fig.2 The influence of relative eccentricity on the bearing capacity of columns under compression

令某一级的相对受压承载力系数为φN，0，其相对偏心距为e0，0/h，其后面相邻几级的相对受压承载力系数为φN，i，相对偏心距为e0，i/h，定义相对偏心距对柱受压承载力影响系数为λc=φN，i/φN，0，相对偏心距增量为Δe0/h=e0，i/h-e0，0/h，则λc-Δe0/h关系更直观体现了相对偏心距对柱受压承载力的影响。从中可以看出，轴心受压长柱稳定系数φ对承载力的影响，在偏心受压长柱的承载力计算中可通过调节相对偏心距e0，0/h 来实现，即其相对偏心距e0，0/h 最小值（其中e0，0含附加偏心距ea）不能低于φ 对应的e0，0/h 值，这样就能把偏心受压长柱和轴心受压长柱的承载力计算方法统一起来。承载力研究表明，可用如下的指数函数较为精确地表达λc-Δe0/h关系：

式中，b为待定系数。

对图2 中的相关数据进行回归分析，得到系数b见表1和图3。可出看出：

（1）当钢筋对短柱轴压承载力的贡献率ξs固定时，b-φN关系曲线呈现明显的两阶段特征：当φN较大时，系数b随φN减小而线性增大；当φN较小时，b-φN关系曲线呈现明显的非线性规律，b 先随φN增大而减小，后随φN增大而增大。这个两阶段特征主要是柱的受力特性从小偏心受压状态转换到大偏心受压状态的体现，非线性阶段的谷底（b最小值处）位于φN=0.35～0.4 的位置，这个位置正好是大小偏心转换位置。

（2）ξs=0.16 时，非线性阶段谷底位置（φN=0.4）的b 值明显小于线性阶段的起点位置（φN=0.9）的b 值，说明大小偏心转换点前后，柱受压承载力受相对偏心距增量的影响最为敏感；ξs=0.25～0.39 时，非线性阶段谷底位置（φN=0.35～0.4）的b值仍明显大于线性阶段的起点位置（φN=0.9）的b值，说明当轴压力最大时，柱受压承载力受相对偏心距增量的影响最为敏感。

表1 λc-Δe0/h关系按指数函数拟合得到的系数bTable 1 Coefficient b obtained by exponential function fitting of λc-Δe0/h

图3 λc-Δe0/h指数函数中的系数bFig.3 Coefficient b in exponential function λc-Δe0/h

根据上述分析，分别用线性函数和二次曲线函数对图3中的两阶段曲线进行拟合：

式中，各系数ai（i=1，2，…，5）与ξs的关系可用二次曲线进行拟合，结果如下：

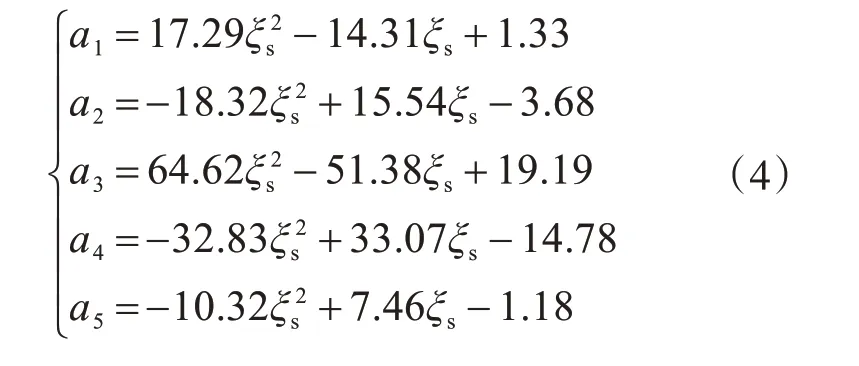
根据式（3）和式（4），取ξs=0.15、0.20、0.25、0.30、0.35、0.40，得到系数b 见表2。可见，表中的b 值在-2.45～-0.67 之间。当取b=-2.5、-2.0、-1.5、-1.0、-0.7 时，由式（2）计算得到的相对偏心距对柱受压承载力影响系数λc见表3。

表2 由式（3）和式（4）计算得到的系数bTable 2 Coefficient b calculated from Eq.（3）and Eq.（4）

2.2 倾斜对框架柱受压承载力的影响系数

按照前述计算整体倾斜效应的等效侧向荷载法，整体倾斜引起的第i 层楼层剪力Vi=ΣγGi。假定按刚度分配与按竖向荷载分配两种情况下的某柱剪力Vij相等，则Vij=γNij（Nij为该柱的轴压力设计值）。侧向荷载作用下的多层框架结构可近似按反弯点法或D 值法［14］计算，设该柱所在层高为H，反弯点高度系数为ρ，则柱端弯矩为Mij=γNijρH，相对偏心距为Δe0/h=Mij/Nijh=γρH/h，代入式（2），得倾斜对柱受压承载力的影响系数为

按照框架结构的反弯点法［14］，底层柱的反弯点高度系数ρ=0.67，上部各层的反弯点高度系数为ρ=0.5，根据常规框架结构柱的截面高度测算，ρH/h 的取值范围在2～8 之间，当ρH/h 取典型代表值5时，柱受压承载力影响系数λc列于表3。

表3 相对偏心距对柱受压承载力影响系数λcTable 3 Influence factor λc of relative eccentricity on compressive bearing capacity of columns

3 倾斜对钢筋混凝土框架梁受弯承载力影响分析

本节采用反弯点法对整体倾斜引起的框架梁弯矩进行分析，进而分析整体倾斜对框架梁受弯承载力的影响。如图4 所示，对于框架中节点，若上、下柱的轴向压力分别为N1和N2，层高分别为H1和H2，反弯点高度系数分别为ρ1和ρ2，倾斜率均为γ，左、右梁的线刚度分别为ib1和ib2，则因整体倾斜引起的节点左梁右端截面的弯矩为

对规则框架的中间各层，若H1=H2=H，ib1=ib2，ρ1=ρ2=0.5，取Nc=（N1+N2）/2，则式（6）简化为

对于边柱节点，则梁端弯矩为式（7）计算值的2 倍。对钢筋混凝土框架梁端截面，其受弯承载力可近似按下式计算：

式中，Fs，b为梁端截面受拉钢筋按屈服强度计算的拉力值；h0，b为梁的截面有效高度。

则整体倾斜对梁端截面受弯承载力的影响系数为

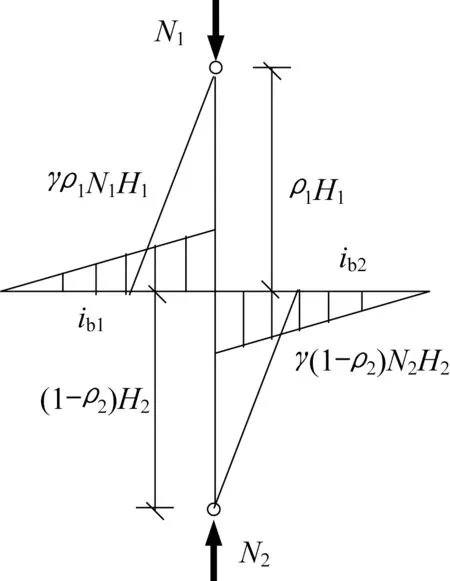
图4 框架中节点的弯矩平衡图Fig.4 Moment diagram of the central joints in frame

考虑到楼面活荷载折减、节点刚域影响等有利因素，整体倾斜引起的梁端弯矩比式（7）计算值有所减小，故上式中考虑了0.8的梁端弯矩折减系数。将式（7）和式（8）代入式（9），得

由式（10）可见，梁端截面受弯承载力影响系数与倾斜率γ、柱轴压力与梁端截面受拉钢筋拉力之比Nc/Fs，b、层高与梁端截面有效高度之比H/h0，b三个因素有关。设后两者的乘积为β=（Nc/Fs，b）（H/h0，b），根据常规框架结构的特征参数估算，β 的取值大致在15～35 之间，根据式（10）计算的倾斜对梁端截面受弯承载力的影响系数列于表4。

4 几点讨论

4.1 关于整体倾斜对不同构件承载力影响程度的比较

文献［6］建立的倾斜对砌体构件受压承载力影响系数计算公式为

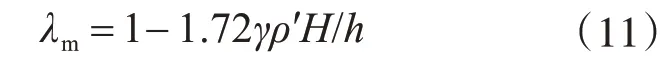
式中，ρ'为砌体构件的计算长度系数（文献［6］以ρ表示，本文为区别于框架柱的反弯点高度系数，改为ρ'）。

对钢筋混凝土框架柱，以b=-1.5 作为典型代表性构件；对钢筋混凝土框架梁，以β=25 作为典型代表性构件；对砌体构件，以高厚比ρ'H/h=9.6作为典型代表性构件。整体倾斜对这三种典型构件承载力的影响系数的比较见图5。可见，砌体构件受影响程度最大，混凝土梁次之，混凝土柱最小：倾斜率γ=0.01 时，λm=0.83，λb=0.89，λc=0.93；倾斜率γ=0.03 时，λm=0.50，λb=0.66，λc=0.80。当然，这种比较是较粗糙的，当构件参数变化时，三者的差异会发生很大变化，特殊情况下甚至会发生影响程度次序上的改变。

表4 倾斜对梁端截面受弯承载力的影响系数λbTable 4 Influence factor λb of inclination on bending capacity of beam end section

图5 倾斜对三种典型构件承载力影响程度的比较Fig.5 Comparison of the influence of inclination on the bearing capacity of three typical members

4.2 关于可靠性鉴定中倾斜影响的考虑方法

上述分析表明，当整体倾斜率为0.003 时，柱受压承载力和梁受弯承载力影响系数均不低于0.95；而当整体倾斜率超过《建筑地基基础设计规范》（GB 50007—2011）［1］规定的允许值0.004 时，部分情况下的承载力影响系数可能低于0.95。《民用建筑可靠性鉴定标准》（GB 50292—2015）［2］规定整体倾斜率超过0.005时，应考虑侧移对混凝土框架构件承载力的影响。从本文分析结论看，这个规定是十分必要且合适的。

《危险房屋鉴定标准》（JGJ 125—2016）［3］分两种情况规定了地基处于危险状态的多层房屋整体倾斜率判断标准：一个是整体倾斜率超过0.01 且梁柱同时发现沉降裂缝；另一个是对三层及以上多层房屋整体倾斜率超过0.02。从前述分析来看，当整体倾斜率为0.01 时，梁、柱承载力影响系数分别在0.84～0.93 和0.88～0.97 之间，变化区间较宽，承载力受到的影响已不容忽视，甚至可能使部分构件变成危险构件；但对框架梁而言，其最易发生弯曲裂缝的位置是梁端截面的顶部，该部位由于板面装饰层等因素不易发现裂缝；对小偏心受压的框架柱而言，柱端也不易发现裂缝。当整体倾斜率为0.02时，梁、柱承载力影响系数分别在0.68～0.86 和0.78～0.93 之间，变化区间很宽，部分构件可能已处于十分危险的状态。因此，危房标准仅以整体倾斜率作为判断是否构成危险房屋的依据显得较为粗糙，很多情况下需要通过考虑整体倾斜影响的承载力精细验算分析才可能发现问题，以便及时处理安全隐患及危险构件。

倾斜对框架梁、柱承载力的影响分析，原则上应采用本文第1 节提出的等效侧向荷载法。因为一方面，相对于第2 节、第3 节的近似方法其计算结果较精确；另一方面，也便于与其他工况计算结果进行组合。特殊情况下，也可采用本文第2 节、第3节的方法进行近似计算。

4.3 关于实际工程应用时一些因素的考虑

从上述分析可知，整体倾斜对混凝土框架梁、柱承载力的影响不容忽视，当然，这是对纯框架结构而言的。钢筋混凝土框架中的砌体填充墙虽然在大震时破坏严重，但在中、小震下能够起到良好的抗侧作用，在抗风、抗整体倾斜影响中发挥很大的作用［15］。因此，对大多数既有混凝土框架结构而言，砌体填充墙的存在可大幅度降低整体倾斜的不利影响。钢筋混凝土框架若采用现浇楼板，板内的分布钢筋对框架梁端截面的抗弯承载力也起到很大的增强作用［15］。在考虑整体倾斜的不利影响时，可考虑这些因素的有利作用，对既有混凝土结构的安全性做出客观、准确且符合实际的评定。作者将在这方面做更深入的研究工作。

另外，还有一个有利因素可予以考虑：整体倾斜引起的结构二阶效应，会在不同结构构件之间产生内力重分布。因此，当考虑整体倾斜引起的结构二阶效应后，若个别或少量构件的承载力有一定程度不足，而同层其余多数构件的承载力仍有余量时，在考虑内力重分布有利影响后，对这些承载力不足的个别或少量构件未必一定要采取加固措施。这方面有待进一步研究探讨。

应该说明的是，实际结构在各部位测得的倾斜不会完全相等，这时可以将实测倾斜分为两部分：先近似取各部位实测倾斜的平均值作为结构的整体倾斜，按本文方法分析整体倾斜对框架结构受力性能的影响；然后，若某些测点的倾斜相对于整体倾斜尚有较大的差值，则可参考文献［4-5］采用相对倾角、角变形等参数分析该倾斜差值对结构产生的影响。当采用等效侧向荷载法分析倾斜影响时，也可将图1 所示竖向悬臂杆模型改为空间框架结构模型后进行更为详细的计算分析：根据各部位的实测倾斜γij（i 为层号，j 为节点号）代替整体倾斜γ 对各节点施加不同的侧向荷载γijGij，再进行空间框架结构内力分析，分析时若不采用楼盖刚度无穷大的假定，则计算结果更精确。

5 结 论

（1）可采用等效侧向荷载法对整体倾斜引起的框架结构附加内力进行分析，每层的侧向荷载可取楼层重力荷载乘以整体倾斜率。

（2）基于反弯点法分析了整体倾斜对钢筋混凝土框架柱受压承载力的影响规律和影响程度。结果表明，倾斜对框架柱受压承载力的影响程度，除了倾斜率外，还受到相对受压承载力系数φN、钢筋对短柱轴压承载力的贡献率ξs、反弯点高度与截面高度之比ρH/h 等因素影响，并建立了倾斜对框架柱受压承载力影响系数的近似计算公式。

（3）基于反弯点法，建立了整体倾斜对钢筋混凝土框架梁受弯承载力影响系数的经验公式。倾斜率、柱轴压力与梁端截面受拉钢筋拉力之比、层高与梁端截面有效高度之比对梁承载力影响系数均有直接影响。

（4）分析表明，由于受不同因素影响，整体倾斜率相同时的框架梁、柱承载力影响系数变化范围均较大。对典型代表性构件而言，砌体构件承载力受倾斜的影响最大，混凝土梁次之，混凝土柱最小。

（5）整体倾斜对钢筋混凝土框架梁、柱承载力的影响不容忽视，应在既有结构可靠性鉴定中予以充分重视。砌体填充墙、现浇楼板作用以及结构内力重分布可降低整体倾斜对框架结构构件承载力的不利影响，尚有待深入研究。