新型矩形钢管混凝土柱-H钢梁节点性能研究
2020-11-12龚永庆黄楚熙龚旭峰刘玉涛段坤朋
龚永庆 黄楚熙 龚旭峰 刘玉涛 段坤朋 徐 晗
(1.中天建设集团有限公司,杭州310005;2.浙江中天恒筑钢构有限公司,杭州310008)
0 引 言
钢结构建筑中方钢管混凝土柱-H 型钢梁梁柱节点有隔板式和环板式。这两类节点存在凸梁凸柱现象,不利于建筑墙体排布和立面处理,且对室内净空也有影响。目前常见的解决方案一是将方柱作扁作长[1],以便埋入墙中;二是参照混凝土L型、T型等异形墙体、柱的做法,进行方钢管异形柱的研究[2-3];三是节点处取消隔板、环板,减小节点容量。
某在建杭州钢结构住宅楼项目,钢框架-钢板剪力墙结构体系,高度99.8 m,实景图见图1。
梁柱节点采用外贴板式节点(以下统称为A型,见图2)在钢梁翼缘两侧各增加一块贴板与钢管柱连接,有效减少了节点处的外凸宽度,方便建筑处理,节点简图如图1 所示。对A 型节点进行微改进,将外贴板内移,与柱外侧箱板平齐,得图3外伸板式B型节点。

图1 在建项目实景图Fig.1 Project overview
矩形钢管柱截面,Q345B 钢材,内灌C60 自密实混凝土。H 型钢梁贴板或伸板厚度8 mm,高度110 mm,伸出柱面长度205 mm,与梁翼缘中对中平齐。钢梁及贴板材质同矩形钢管。B 型节点的梁宽为184 mm。A、B 型截面节点几何尺寸见图2、图3,本文就这两类节点在不同轴压比、低周反复荷载作用下的节点性能进行分析,最后对节点的加工制作及建筑使用性方面作简要论述。该项目研究依托中天建设集团2016 年度技术研发项目【编号:ZTYF-2016-09】。
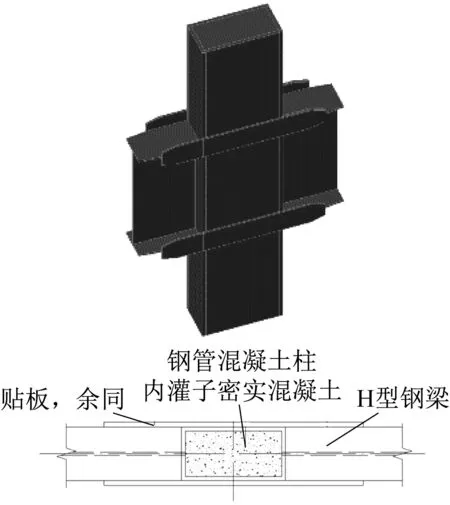
图2 贴板式节点(A型)Fig.2 A type
1 有限元模型
1.1 模型构造及参数设计
本文以中柱单向连接节点为研究对象,模型主要包括外约束方钢管、柱内混凝土、钢梁、贴板或伸板等部分,模型试件的几何构造如图2、图3所示。钢梁的上、下翼缘钢管外壁双面角焊缝连接,贴板或伸板内侧与钢梁翼缘交叠区双面角焊缝连接。
分析不同钢管截面及配套钢梁截面的节点在纯弯和压弯两种受力状态下的结构特性,压弯状态下考虑不同轴压比,根据《钢结构设计标准》[4]规定,钢管混凝土柱抗震等级为二级,轴压比限值为0.8,节点试件参数如表1所示。
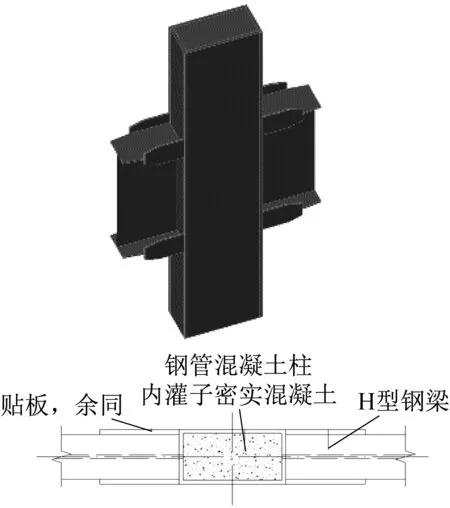
图3 伸板式节点(B型)Fig.3 B type
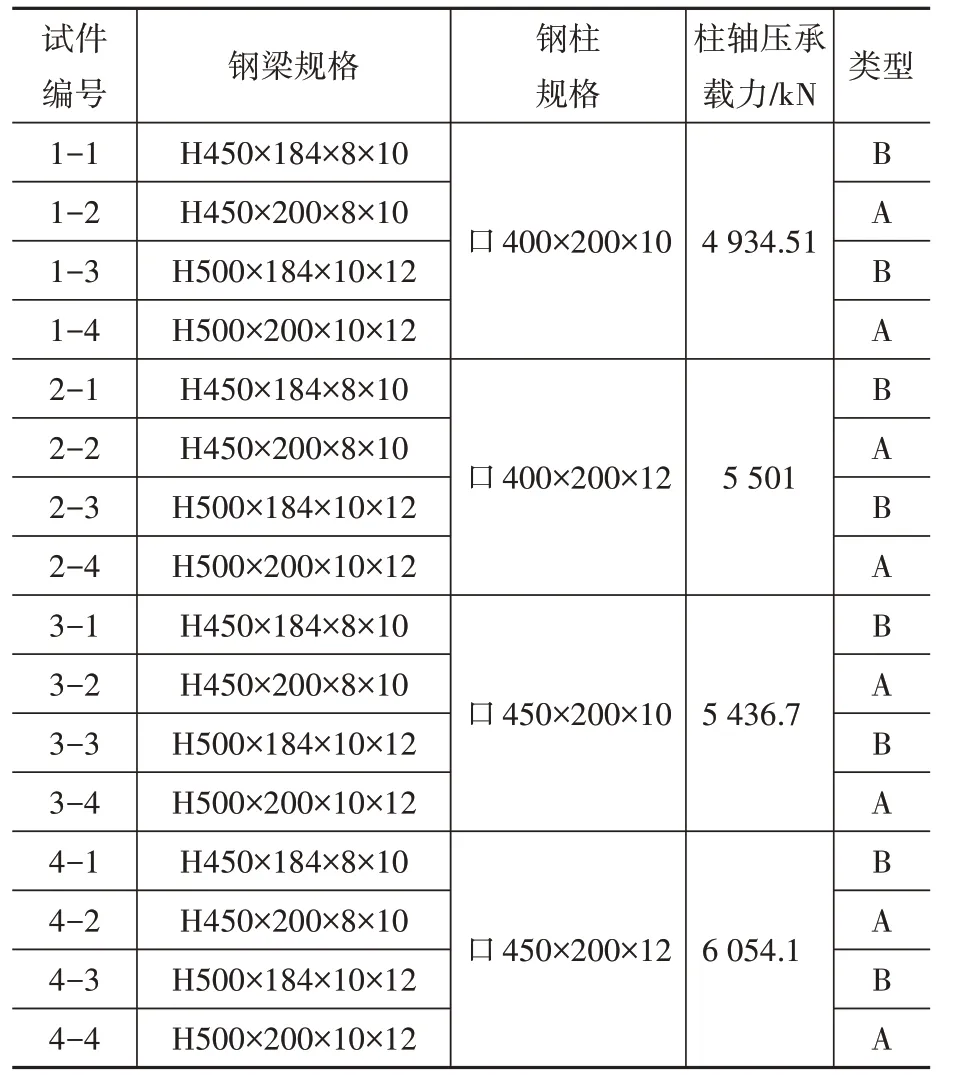
表1 试件参数Table 1 Component parameter
1.2 有限元建模参数
1.2.1 材料本构关系
采用Abaqus 有限元软件进行数值模拟。材料本构参照韩林海和杨有福[5]的方法构建,钢材及混凝土塑性应力应变曲线见图4-图6。
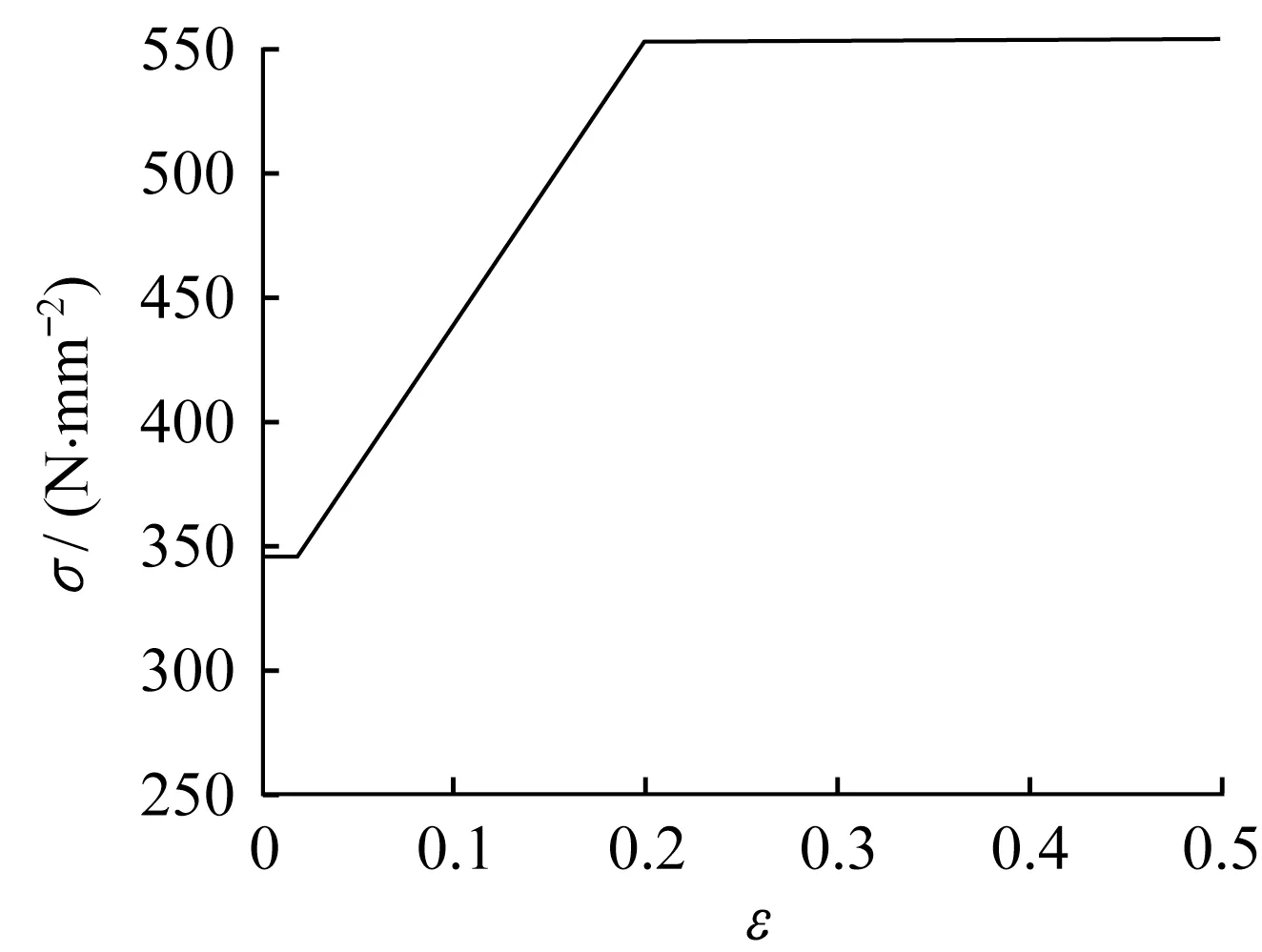
图4 Q345塑性σ-ε曲线Fig.4 Plastic stress and strain curve of Q345 steel

图5 C60混凝土压缩塑性σ-ε曲线Fig.5 Compression plastic σ-ε curve of C60 concrete
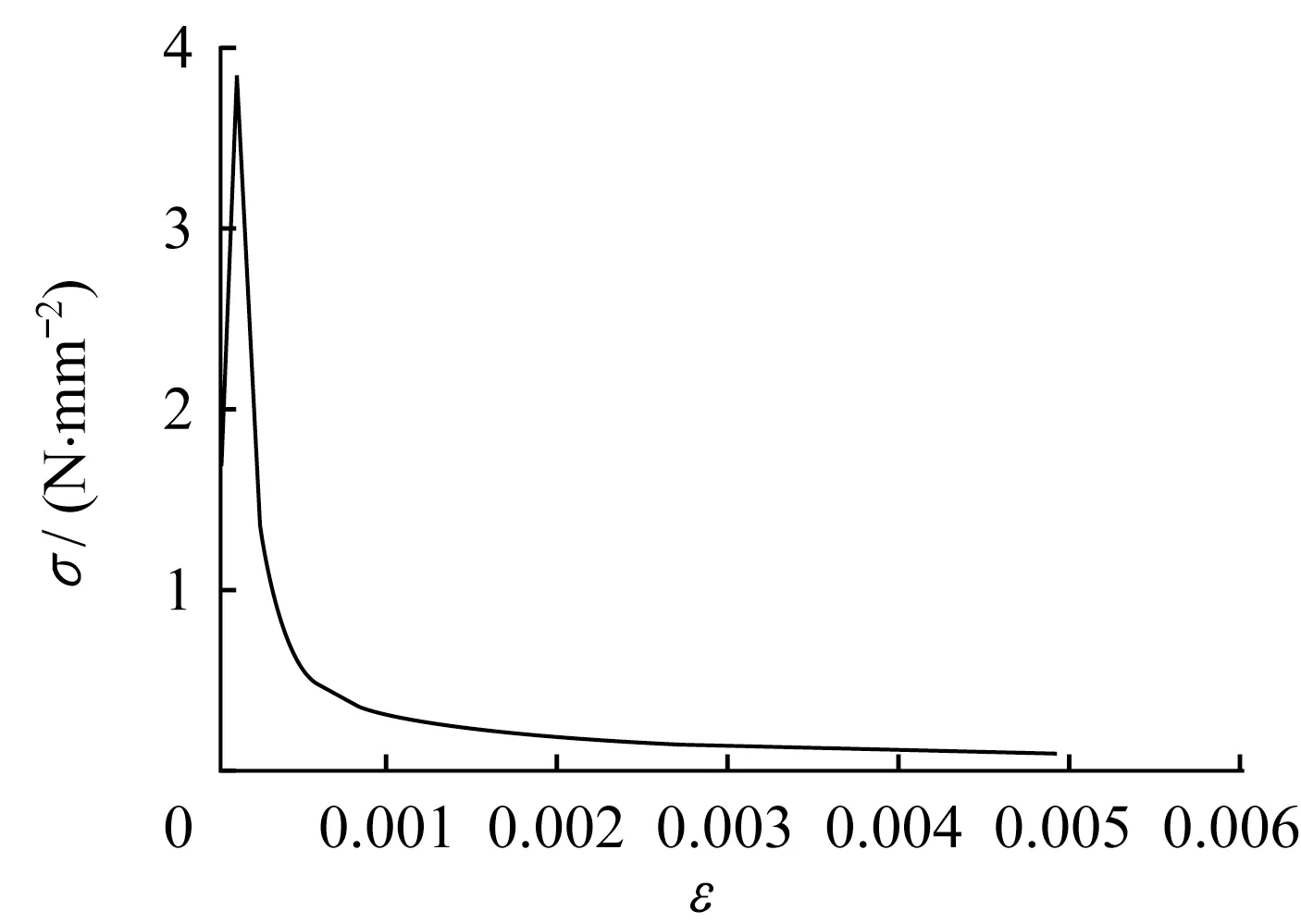
图6 C60混凝土拉伸塑性σ-ε曲线Fig.6 Tension plastic σ-ε curve of C60 concrete
1.2.2 单元类型及接触、约束边界条件
模型采用二次三维实体单元,钢结构及混凝土采用8 节点减缩积分格式的C3D8R 实体单元。单元网格划分尺寸在经过试算并考虑求解速度和精度的基础上确定,节点模型网格划分如图7所示。
钢管与混凝土的接触之间采用Abaqus 的面面接触,法向方向两者不能相互穿透,切向方向考虑库伦摩擦,普通钢板与混凝土摩擦传递系数取0.6[6]。柱两端铰接,并限制平面外转动。压弯状态下柱底部铰接并约束平面外转动自由度,柱顶约束X、Y 向平动及面外转动自由度,边界条件示意图如图8所示。

图7 模型网格划分Fig.7 Meshing of model
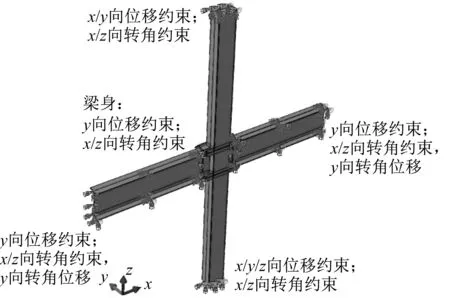
图8 边界条件示意图Fig.8 Boundary conditions
1.2.3 循环加载
柱顶施加轴力,梁端施加低周反复位移荷载。根据霍静思[7]的研究,节点加载方式对力学性能并无明显影响,采用转角位移加载模式,时长160 s,分20 级,每一级循环两次,控制梁端加载最大转角0.046 4 rad,加载模式见图9。
2 有限元分析结果
计算过程分两个步骤:先施加柱顶轴力,再施加梁端转角位移,全程打开大变形开关。
2.1 弯矩-转角滞回曲线及特征分析
图10给出了各轴压比下试件的弯矩-转角滞回曲线。曲线形状饱满,没有捏拢现象,随着轴力的增加,节点耗能滞回环逐渐变扁。纯弯节点耗能能力最优,轴压比0.1~0.5 时,耗能能力逐渐下降,轴压比在0.6 及以上时,耗能能力显著下降。总体上两类节点都表现出了良好的耗能性能。
图11 给出了在轴压比0.1 下两类节点的滞回环对比。两类节点的极限转角基本相同,极限弯矩A 类略大于B 类,原因分析在于B 类节点为了空间牺牲了部分梁宽,导致截面刚度不如A 类。但两者的滞回曲线走势基本一致,无特殊差别。
当前常用的耗能性能评价指标[8]为能量耗散系数E和等效黏滞阻尼系数ζeq。两个参数的计算如图12及式(1)、式(2)所示。
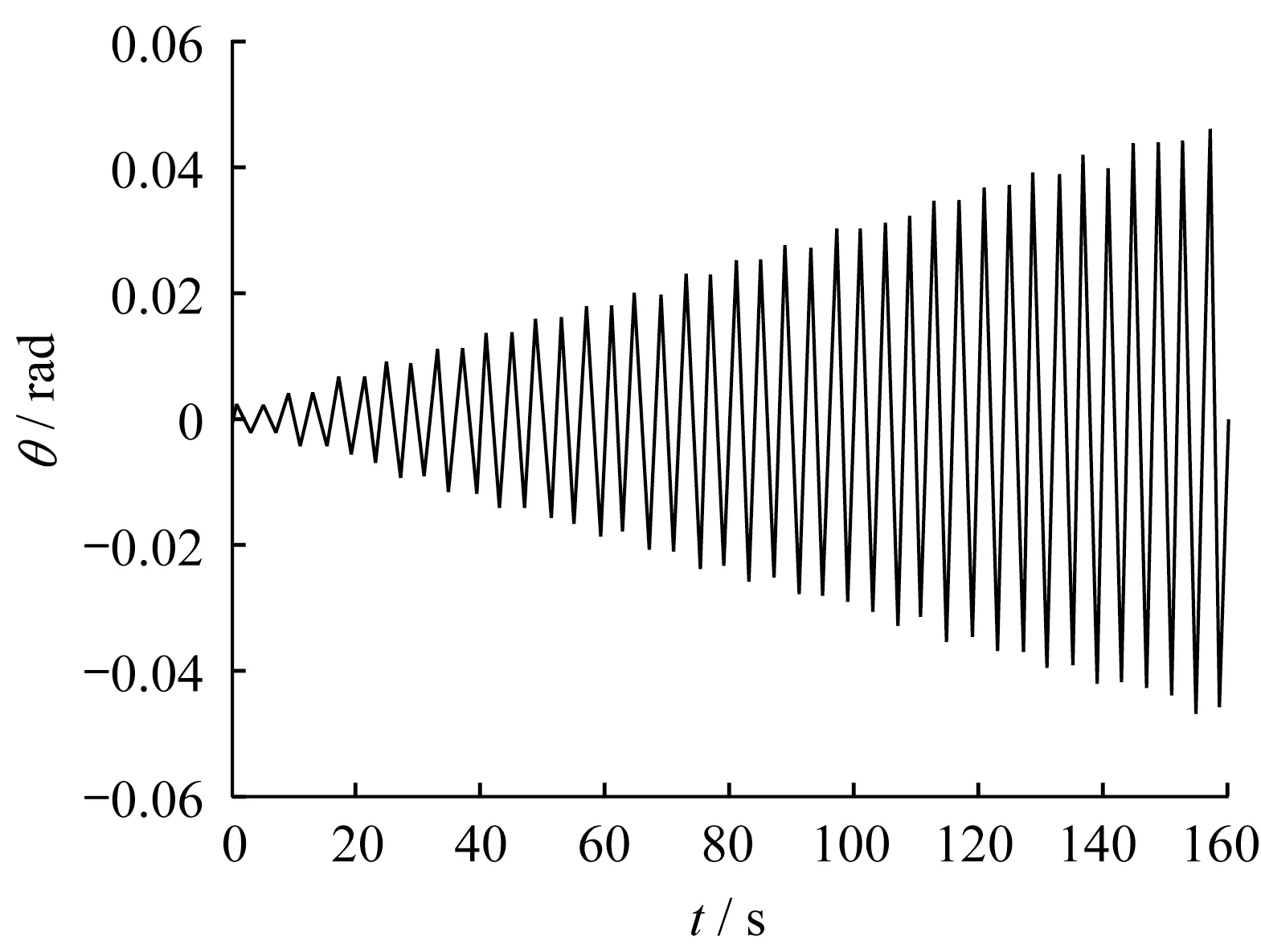
图9 梁端竖向往复位移加载曲线Fig9 Vertical reciprocating displacement loading curve

图10 节点弯矩-转角(M-θ)滞回曲线Fig.10 Moment-angle hysteresis curve
图13、图14 给出了各试件的耗能性能参数。试件的能量耗散系数E取2.1左右,等效黏滞阻尼系数ζeq取0.33 左右,根据相关研究结果表明,钢筋混凝土节点的等效黏滞阻尼系数ζeq在0.1 左右,型钢混凝土节点的等效黏滞阻尼系数ζeq在0.3左右,本文A、B两类试件的能量耗散系数和等效黏滞阻尼系数数值相近,且均大于型钢混凝土节点的等效黏滞阻尼系数,表明试件的耗能性能良好,满足结构抗震设计要求。

图11 轴压比0.1下两类节点弯矩-转角(M-θ)滞回曲线对比Fig.11 Moment-angle hysteresis curve comparison of two types with axial pressure ratio 0.6
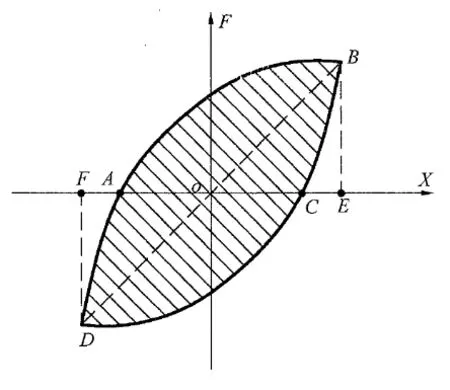
图12 等效黏滞阻尼系数计算Fig12 Equivalent viscous damping coefficient calculation


图13 能量耗散系数Fig13 Energy dissipation coefficient
2.2 骨架曲线分析
图15给出了依托滞回曲线得出的弯矩-转角骨架曲线,各试件的骨架曲线正反向基本对称,经弹性变形后进入承载力强化阶段和弹塑性阶段。表2给出了轴压比0.1下的试件屈服、极限及延性指标,其余轴压比下试件特性类同,此处不再罗列。
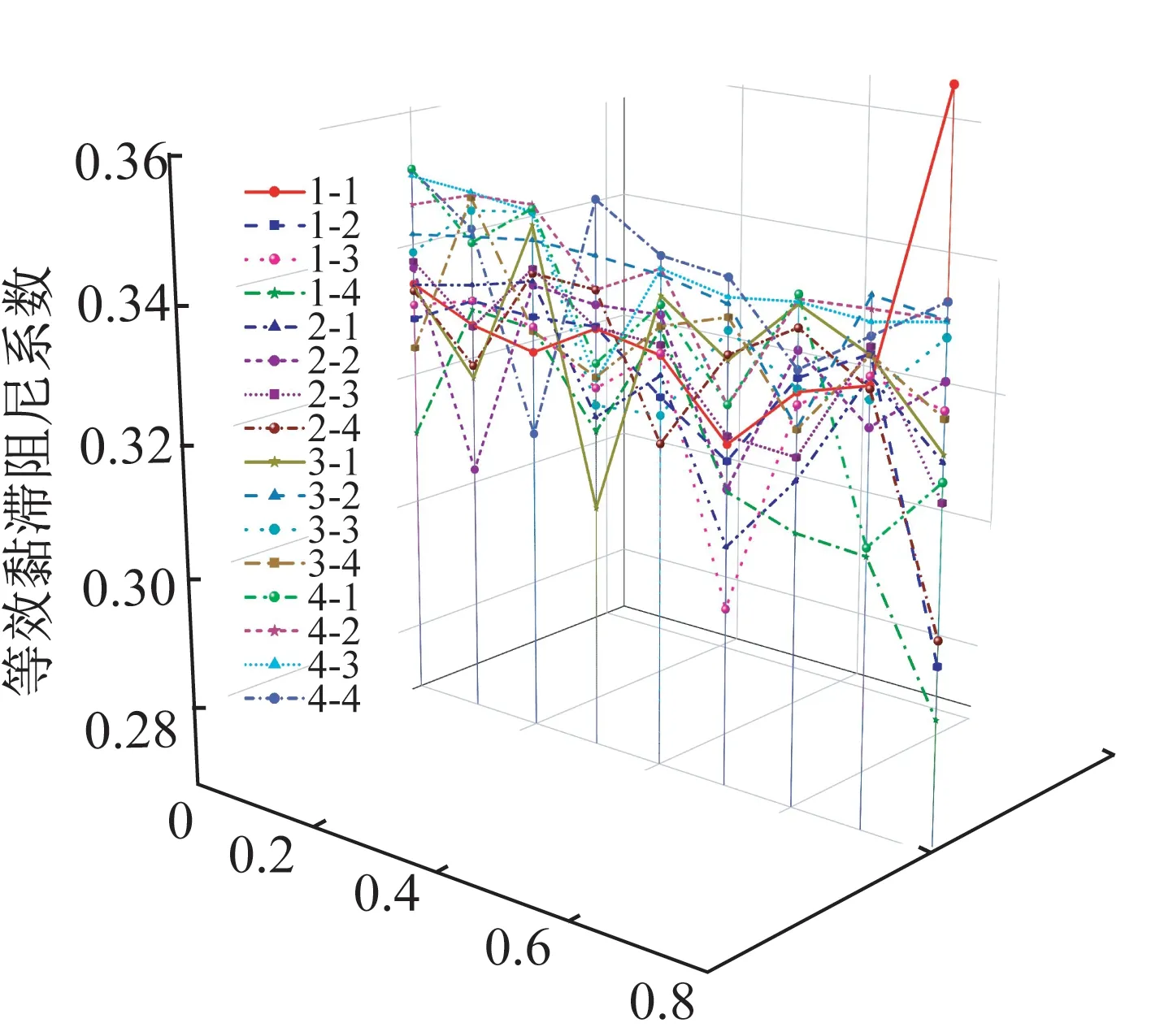
图14 等效黏滞阻尼系数Fig14 Equivalent viscous damping coefficient

表2 各试件屈服、极限及延性指标Table 2 Yield,limit and ductility of components
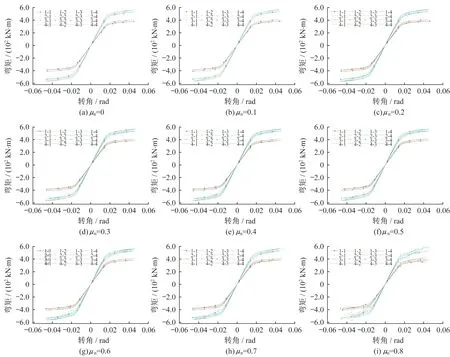
图15 不同轴压比下节点弯矩-转角(M-θ)骨架曲线Fig15 Moment-angle skeleton curve under different axial pressure ratio
由图15 及表2 可知,各试件屈服转角在0.016rad 左右,随着钢梁截面的变大,屈服弯矩增大,高度相同的A 类截面屈服弯矩大于B 类截面,各试件延性系数在2.6~2.9之间,满足钢筋混凝土结构对延性系数不小于2的要求。
2.3 等效刚度分析
各轴压比下试件的等效刚度退化曲线,见图16。可知,各试件在正负两个方向等效刚度退化规律大体相似,加载初始的弹性阶段,等效刚度基本保持不变或有缓慢下降,随后刚度退化速度开始加快,从开始屈服到强化阶段,等效刚度退化速度最快,随着试件进入弹塑性阶段,刚度退化速度减缓,刚度退化主要是由试件局部的塑性发展和破坏位置的损伤累积所引起。各试件初始正向刚度和初始负向刚度并不完全相同,大体上初始正向刚度略大于初始负向刚度,随着轴压比的升高,各试件的初始刚度都略有增大,比较A、B 两类节点,在相同梁截面高度和相同轴压下,A 类的初始刚度大于B 类,以试件1-1 和1-2 为例,A 类的1-2试件较B类的1-1试件初始刚度大了10%,主要因为B类钢梁的截面宽度小于A类。
2.4 应力分布及破坏形态
图17 给出了试件(以试件1-1、1-2 为例,轴压比0.1情况下)从加载初直到破坏的全过程应力分布及变化情况(0 s,40 s,80 s,120 s,160 s 五个时点)。
可知,在循环荷载作用下,首先在节点核心区强度、变形开始增长,紧接着核心区钢梁翼缘开始屈服,柱两侧的贴板或伸板也开始屈服,随着加载深入,塑性区开始往梁外侧和腹板扩展。满足刚性节点塑性区外移的要求。
对比A、B 两类节点塑性开展,都开始于贴板或伸板的屈服,此处为节点的薄弱点。B 类节点由于伸板不连续,塑性开展传递至钢管外壁,并慢慢在核心区形成斜十字交叉的应力带,A 类节点由于侧板的连续,塑性开展先经有侧板传递给两侧的钢梁,部分传递至钢管外壁,但大部分都由侧板自身承担,钢管作用未能有效发挥。

图16 不同轴压比下节点等效刚度退化曲线Fig.16 Stiffness degradation curve under different axial compression ratio
2.5 规范对刚性节点的要求
《建筑抗震设计规范》(GB 50011—2010)(以下简称“抗规”)8.2.8条规定[9],对以抗弯控制为主的钢结构刚性连接,要满足式(3)的要求。

对本文试件做如上复核,结果如表3所示。
抗规表8.2.8 要求Q345 钢材牌号下,梁柱焊接的刚性连接要求ηj为1.3,表3 的结果表明A、B类节点不满足刚性连接的要求,从有限元分析结果看,两类节点都满足强节点、弱构件的准则,且塑性区都有效外移,从概念上看都满足刚性节点的要求,不满足抗规的计算要求,这与构件的高度、板件的厚度及钢材牌号等都相关,后续可以就这些方面开展更深入的研究。

表3 节点刚性验算Table 3 Rigidity check of joints
3 工艺及适用性比较
A、B 型节点都可在工厂加工制作完成,包括牛腿、贴板或侧板。B 型节点的焊缝数量相对较少,且伸板的材料用量少于贴板,一定程度能节约钢材。另外,在相同柱宽条件下,B 型节点的钢梁宽度能做得更小,有利于空间的节省和利用,且不存在外凸的问题,也有利于砌体、门窗等的连接,示意图见图18。另外,贴板由于与柱是面外连接,力与变形的传递没有伸板类连接直接有效,且面外传递有增加节点处钢管壁的失稳风险。综合以上两条,B型节点具备一定的优势。

图17 试件节点核心区应力随位移加载变化分布Fig.17 Variation distribution of stress with displacement in core area of each component

图18 贴板或侧板式节点与墙体关系Fig.18 The relationship between the joint and the wall
4 结 论
通过实际项目的实施和改进,对新型的矩形钢管混凝土柱-H 型钢梁节点进行微改进,得到形式略微不同的另一种适用于钢结构住宅的节点。比较分析不同轴压比下两类节点的Mises 应力、滞回曲线、骨架曲线、等效刚度退化曲线及比较规范对刚性连接的要求,结合相关性能参数及工艺、适用性,结论如下:
(1)两种节点的滞回曲线都很饱满,都表现出优异的耗能能力,从节点应力云图可知,两类节点的塑性开展过程大体相似,侧板或贴板的存在有效缓阻了节点核心区的塑性开展,符合强节点弱构件的概念要求。
(2)各轴压比下试件的等效刚度退化曲线,正负两个方向等效刚度退化规律大体相似,各试件初始正向刚度和初始负向刚度并不完全相同,大体上初始正向刚度略大于初始负向刚度,随着轴压比的加大,各试件的初始刚度都略有增大,比较A、B两类节点,由于A类节点较大,在相同梁截面高度和相同轴压下,A类的初始刚度大于B类。
(3)节点的损坏都出现在钢梁处,且贴板或伸板有效地外移了钢梁的塑性区域,保证了节点的安全,但文中的节点构件截面形式并不满足抗规关于刚性连接的计算要求。
(4)施工工艺方面两者都可以工厂化制作加工,B 型节点的焊缝数量相对较少,且伸板用料少,能节约部分钢材,并较A型节点在空间要求方面更少。因而,在一定程度上,其适用性会更广。
(5)节点的力学性能当前局限于理论和数值模拟,需试验数据进一步论证。
