基于随机骨料模型的混凝土弹性模量概率密度分布研究

袁卫国 李亚春 李 贲 曾祥茂 朱克东 罗祝君

（广州市第一市政工程有限公司，广州510060）

0 引 言

ABAQUS CDP（Concrete Damage Plasticity）模型被广泛地应用于混凝土及钢-混凝土组合结构的非线性有限元数值模拟分析中［1-3］，该模型将混凝土宏观特征的非线性本构关系作为有限元单元的性质（细观尺度特征）而参与迭代分析计算，这种处理方法没有考虑组成模型的单元的个体性差异（非均质性），所以有限元数值模拟计算结果不存在宏细观尺度上的差异［4-5］，无法得到混凝土材料非均质性对某一变量的定量影响结果。混凝土材料往往存在各种自身缺陷，例如孔洞和微裂纹等，而且各组分材料的力学性质参数具有一定的随机性和离散性，而不是通常计算时所采用的定值［6-7］。大多数文献研究将混凝土视为三相复合材料，对每一相材料赋予单一的材料属性，且主要利用二维随机骨料模型模拟混凝土构件的断裂破坏［8-12］，很多学者对三维随机骨料模型的建立提出了新的不同的方法［13-15］。到目前为止，尚未有学者对基于塑性损伤和三维随机骨料模型的混凝土弹性模量概率密度分布进行研究。基于此，本文将混凝土视为一相非均质材料，通过ABAQUS 自带的CDP 模型模拟混凝土的塑性损伤开裂破坏，通过三维随机骨料模型模拟混凝土的非均质性，对两种概率密度分布下的弹性模量进行分析研究，通过与文献试验对比，给出了两种分布下描述混凝土非均质性的参数取值范围，为研究混凝土的非均质性提供了一定的参考。

1 理 论

1.1 正态分布随机变量X的概率密度

正态分布随机变量X的概率密度为

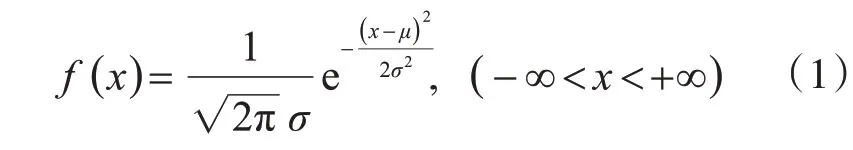
式中，均值μ及标准差σ(σ ＞0)都是常数。

均值μ=100 时不同标准差对应的概率密度函数如图1所示。

1.2 Weibull分布随机变量X的概率密度

Weibull分布随机变量X的概率密度为

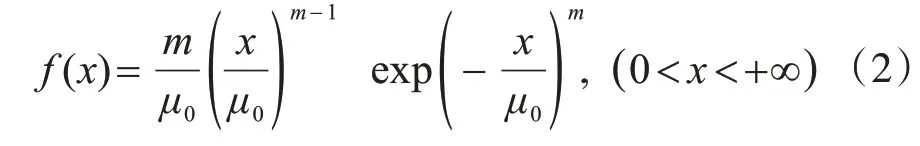
式中，m 和μ0都是常数，m 表示Weibull 概率密度分布的均质度，反映随机变量x 取值的离散程度；μ0是一个与自变量平均值有关的参数，表示Weibull概率密度分布的数值尺度，其数值并不等于自变量平均值。μ0=100 时不同均质度密度函数如图2所示。

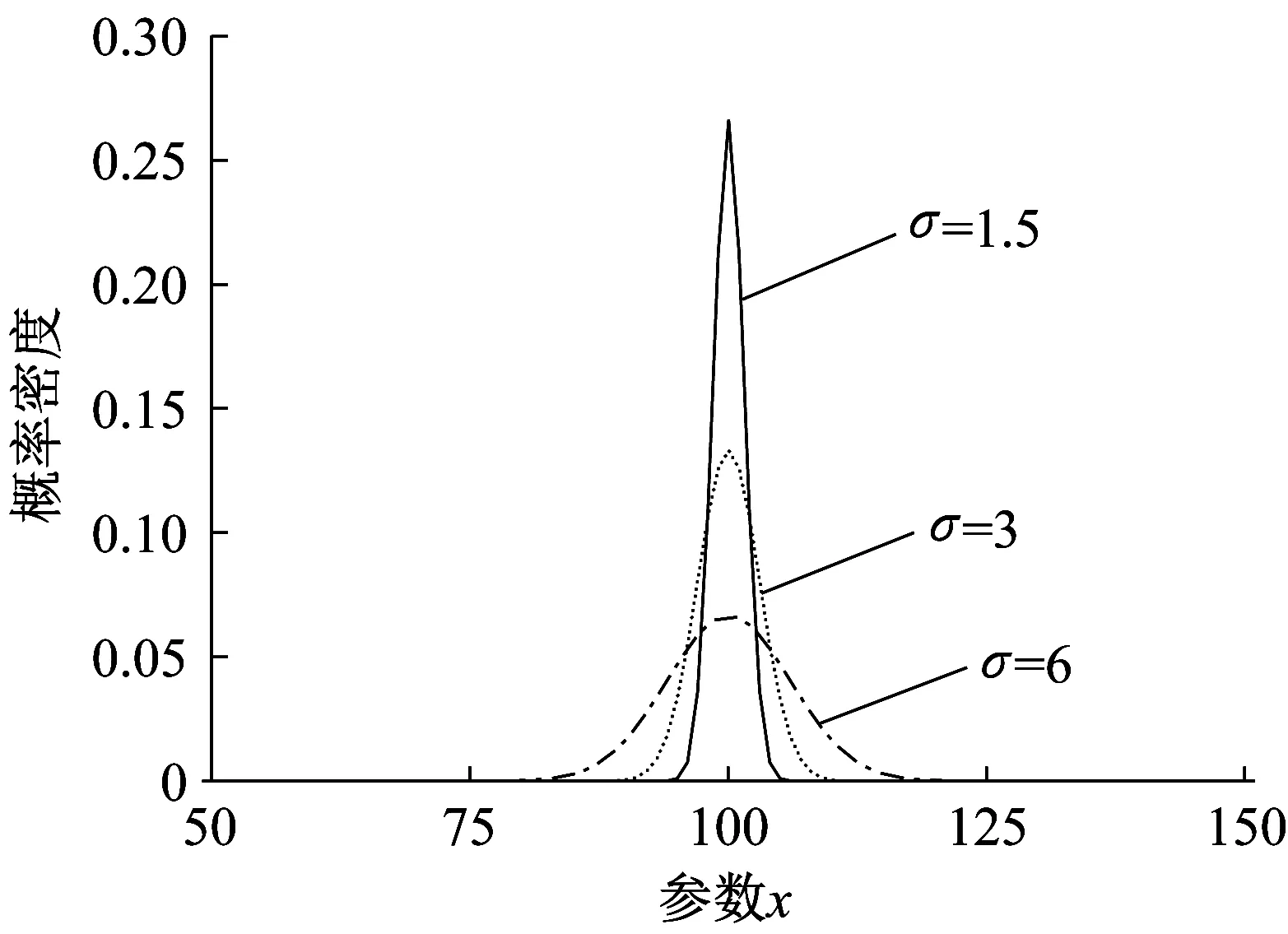
图1 μ=100时不同标准差对应的概率密度函数Fig.1 Probability density function of different standard deviations with μ=100

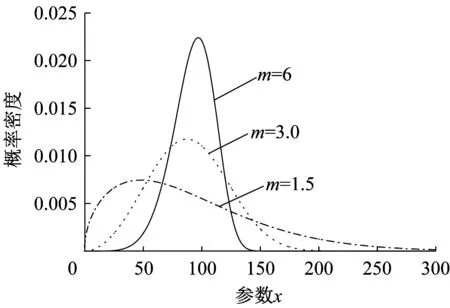
图2 μ0=100时不同均质度概率密度函数Fig.2 Probability density function of different homogeneities with μ0=100

1.3 混凝土应力应变关系

ABAQUS中的损伤模型是一个基于塑性力学的连续介质损伤模型，其中混凝土应力和应变关系如下所示：

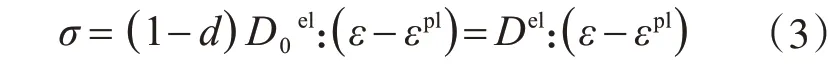
1.4 塑性流动法则

ABAQUS 塑性势函数采用了双曲线数学模型，该模型基于非关联的塑性流动准则，其数学关系式如下所示：

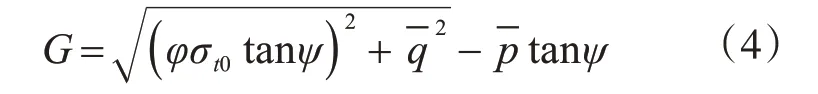
式中，参数φ(θ，fi)是一个表示偏心的参数，ABAQUS中其默认值为0.1；σt0(θ，fi)=σt|-εplt=0为计算之前设定的表示初始损伤时的单轴拉伸应力值；ψ(θ，fi)为在三维应力空间中p-q所确定的平面上在高侧压力作用下的以角度表征的扩容角=表示第四强度理论的Mises 等效有效应力，-S= -p·I+ -σ 表示应力空间中有效应力张量的偏分量；=表示三维应力空间有效静水压力，其中I为应力不变量。

1.5 三维塑性屈服空间函数

屈服函数F(-σ，ε͂pl)表征一个三维空间函数，它可以计入材料在拉伸和压缩状态下材料强度值的不同变化规律，有效应力三维空间屈服函数的屈服面演化规律由等效塑性应变-εtpl和-εcpl来表征控制，其关系式如下式所示：

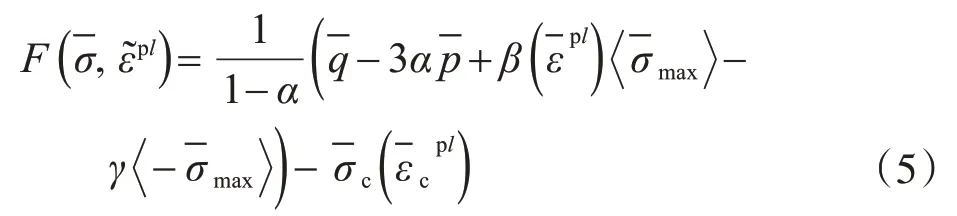
式中，α 由Kupfer 曲线折算而求出，其值等于双轴抗压与单轴抗压极限强度的比值第四强度理论Mises 等效应力，其中为的应力偏张量=-：I为有效应力，I 为应力不变量；其中和分别为塑性拉应变和塑性压应变和分别为有效抗拉强度和有效抗压强度；符号表示=(|x+x)，表示-σ代数特征值的最大值；γ表示第二应力不变量在三维空间拉伸子午屈服面和压缩子午屈服面取值的比值。

2 MATLAB模型和ABAQUS模型

为了保证本文数值模拟数据的可靠性和有效性，本文按照文献［16］建模，如图3所示为试验三点弯曲钢筋混凝土梁，梁尺寸为3 m×0.2 m×0.45 m，梁底端向上偏移40 mm 处放置有3 根直径为20 mm的钢筋。按文献［16］设置材料属性，钢筋弹性模量为2.1×105MPa，泊松比为0.3，受拉屈服强度为500 MPa，不考虑受压和受拉损伤；混凝土宏观尺度上的弹性模量为3.35×1010Pa，骨料弹性模量由概率密度函数随机生成，骨料泊松比取0.2，混凝土每一颗骨料都采用塑性损伤本构模型，粘滞系数设置为0.000 5，断裂能为76.5 N/m，抗压强度和抗拉强度分别为为38 MPa 和3.5 MPa。利用MATLAB 中normrnd 和wblrnd 命令随机生成服从正太分布和Weibull分布的数据作为弹性模量，利用PYTHON 语言将弹性模量数据导入ABAQUS中，将每一颗骨料赋予不同的弹性模量，混凝土塑性损伤参数如图4 所示；为了减小跨中加载点处的应力集中，在ABAQUS 有限元模型加载点处设置一刚性垫块，尺寸为0.2 m×0.2 m×0.2 m，弹性模量为2.1×106MPa，泊松比为0.3。钢筋采用T3D2单元，混凝土随机骨料和垫块采用C3D8R 单元。在垫块正上方15 mm 处建立参考点，对垫块上表面和参考点建立耦合约束，由于塑性损伤本构迭代运算极不容易收敛，因此本文对参考点进行位移加载。钢筋与混凝土的接触设置为embedded，垫块与混凝土的接触设置为tie，三点弯曲梁两端支座约束为固定约束，采用自行编制的MATLAB程序建立模型，MATLAB 中三维随机骨料模型如图5所示（骨料最小粒径10 mm，最大粒径20 mm，共计8 000 颗），与MATLAB 模型对应的ABAQUS有限元模型如图6所示。

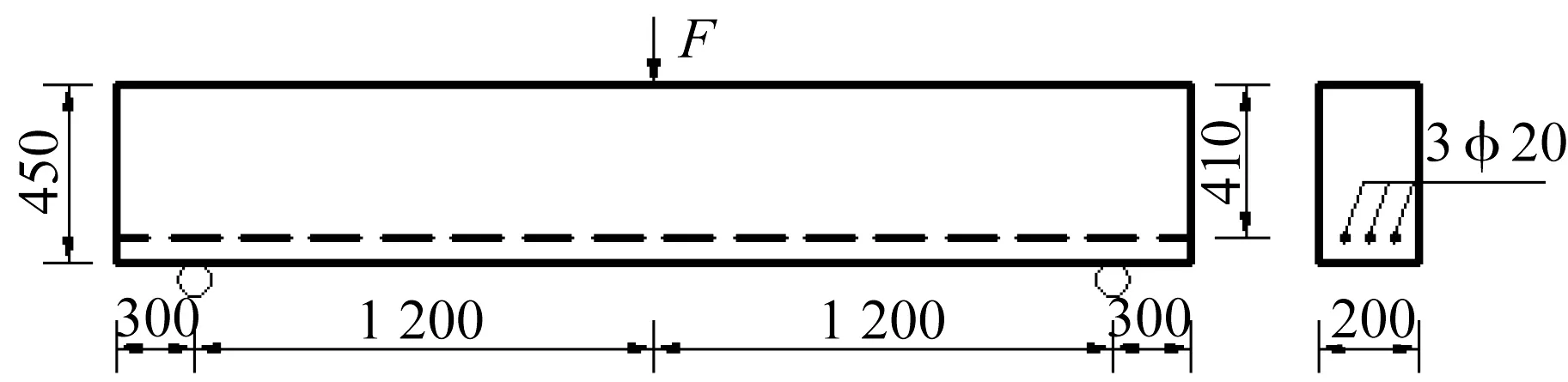
图3 文献［16］三点弯曲梁（单位：mm）Fig.3 Three-point bending beam in Ref.［16］

利用MATLAB 语言编制三维随机骨料投放程序，生成骨料的空间位置和粒径信息并输出到TEXT 文档，利用PYTHON 语言参数化建模流程如下：

（1）利用PYTHON 语言将骨料信息导入到ABAQUS有限元软件中；

（2）利用PYTHON 语言中的For 循环和Range（）遍历函数建立每一颗骨料的part模型；

（3）利用PYTHON 语言中的For 循环和Range（）遍历函数对每一颗骨料赋予材料属性；

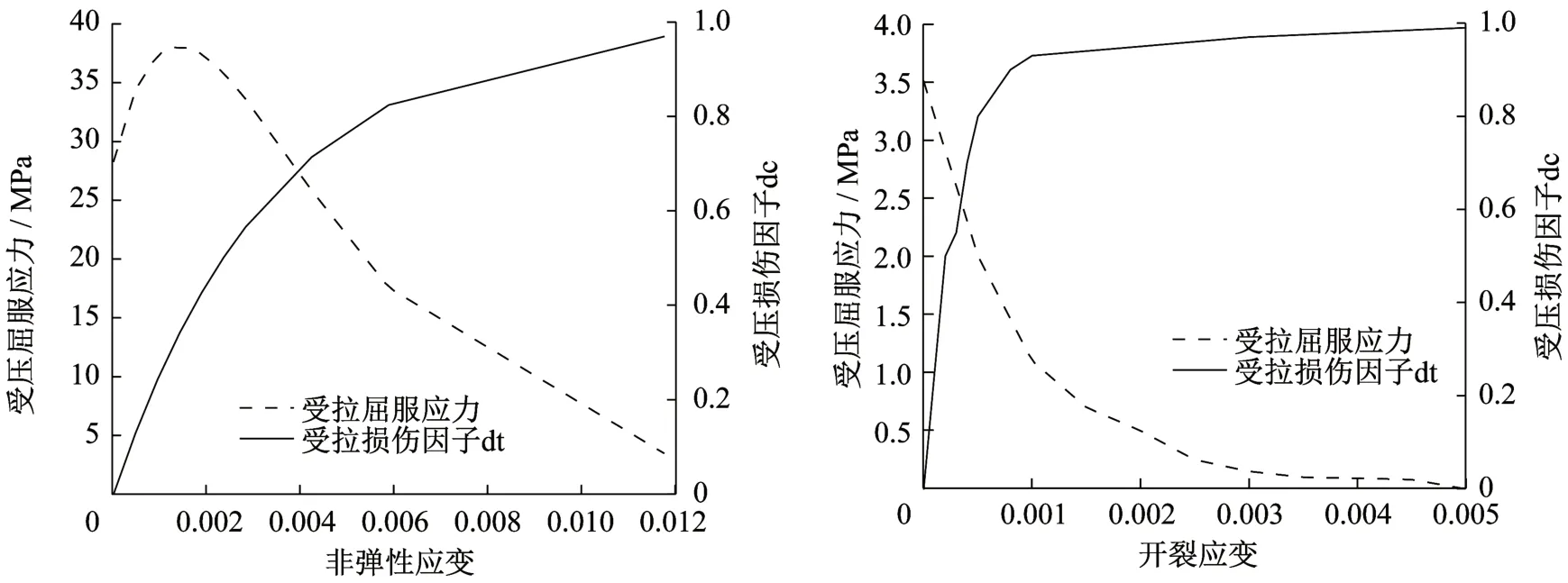
图4 ABAQUS塑性损伤参数Fig.4 Plasticity damage parameters in ABAQUS

（4）利用PYTHON语言中的For循环和Range（）遍历函数将每一颗骨料装配到assembly模型中；

（5）由于骨料与梁构件的空间重合，利用PYTHON 语言中的For 循环和Range（）遍历函数依次用每一颗骨料进行布尔cut操作，即在有骨料的位置处切割形成孔洞；

（6）利用PYTHON语言中的For循环和Range（）遍历函数依次将每一颗骨料重新装配到assembly模型相应的位置；

（7）利用PYTHON语言中的For循环和Range（）遍历函数将骨料和切割后的梁构件进行布尔merge操作。

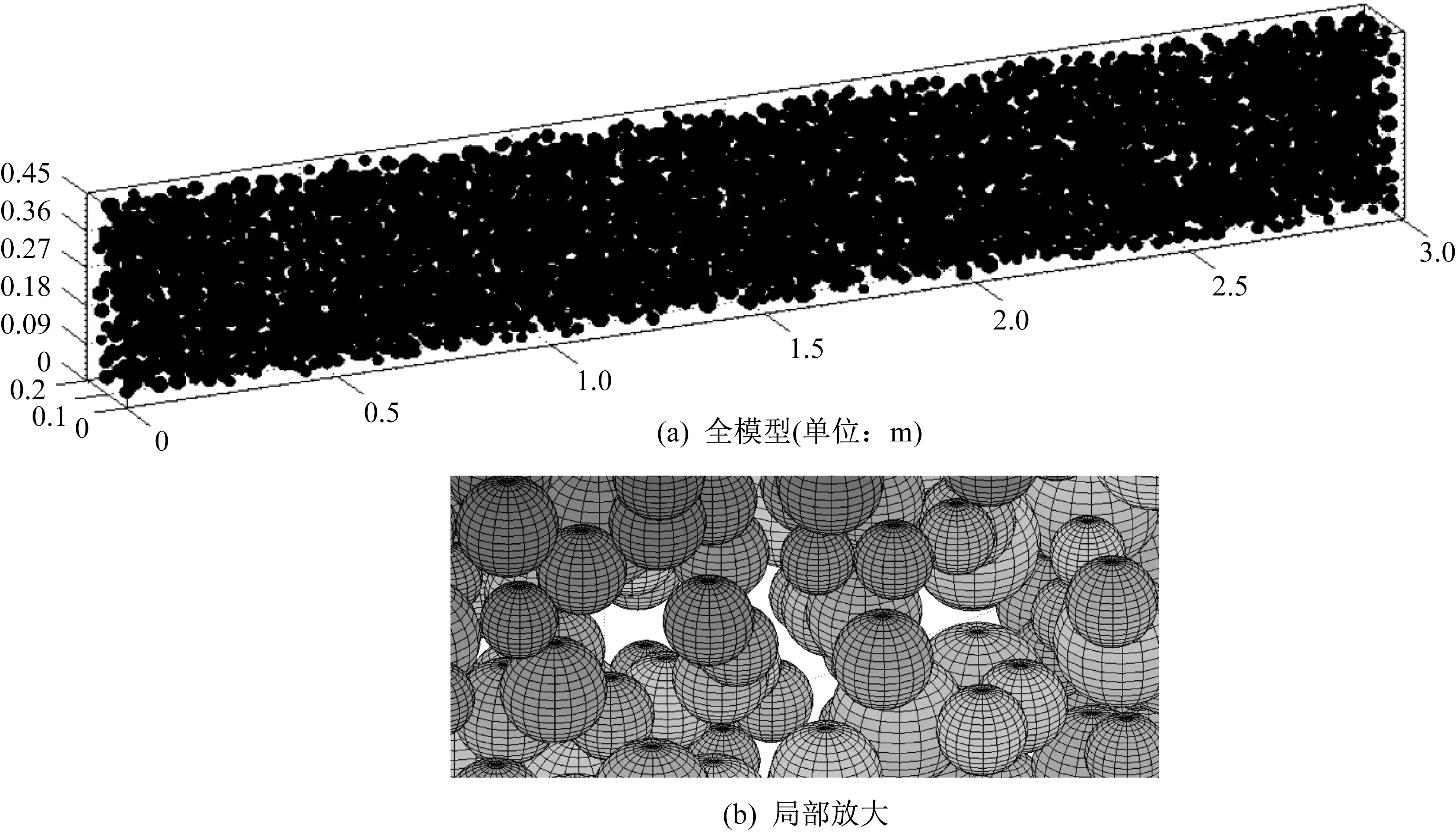
图5 MATLAB随机骨料模型Fig.5 Random aggregate model in MATLAB

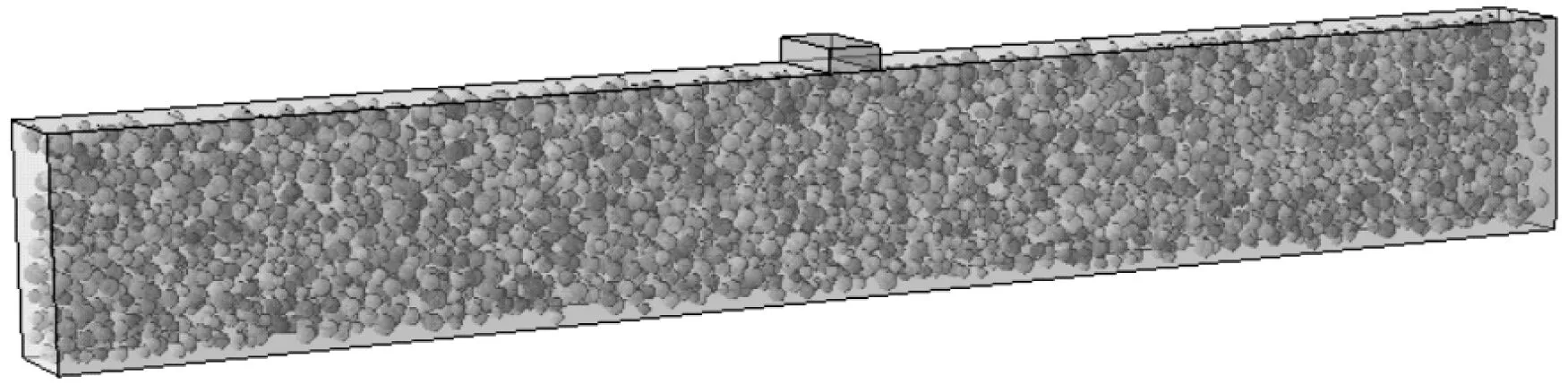
图6 ABAQUS随机骨料模型Fig.6 Random aggregate model in ABAQUS

3 数值模拟与试验对比分析

如图7 所示为不同工况下损伤云图，括号内的数据为本文数值模拟得到的三维随机骨料钢筋混凝土梁的极限承载力。

本文数值模拟梁跨中右侧斜裂缝基本呈45°扩展，通过图7 和图8 对比可以看出，本文数值模拟和文献［16］裂缝扩展形态基本吻合。从图9 可以看出荷载位移曲线有明显的突变点，各种工况荷载-挠度曲线在突变点之前基本完全一致，突变前为直线，突变后曲线斜率越来越小，图9 给出了试验六根梁1/2 结构的荷载-挠度曲线，其平均值为369.4 kN，图7 所示工况最小极限荷载为335.792 kN，最大极限荷载为337 kN，最小误差为8.8%，最大误差为9.1%，说明本文建立的基于非均质性和塑性损伤模型的有限元数值计算模型是可行和有效的。

虽然正态分布能表征混凝土的非均质性，但是由于其标准差取值往往在107数量级左右才能表征混凝土的非均质性，因此笔者建议考虑混凝土非均质性时，采用Weibull 概率密度函数，下面对Weibull均质度取值进行分析。

图7 不同工况损伤云图Fig.7 Damage contour of different cases

图8 文献［16］试验裂缝扩展形态Fig.8 Crack propagation mode of experiment in Ref.［16］

4 Weibull分布均质度取值分析

从图10 和图11 可以看出，随着Weibull 分布均质度m 取值的不断增大，混凝土宏观尺度上的弹性模量值将接近于细观尺度上的弹性模量值的平均值。将MATLAB wblrnd 命令生成的混凝土弹性模量值用相应Weibull 分布的均值进行均一化处理，不断调整均质度m的取值范围后发现，当均质度在1到200之间时，用单调增函数指数函数拟合均一化后弹性模量与均质度m 的关系，可以得到如图10 所示的拟合关系式（6）（E0为Weibull分布的均值），但拟合效果较差。当均质度取值范围在1～50 之间时，可以得到如图11 所示的拟合关系式（7）（E0为Weibull 分布的均值），此时拟合效果较好，这两个拟合方程分别如下所示。

在进行混凝土非均质性数值模拟时，混凝土弹性模量均值和均质度可以根据上述拟合公式进行选取。

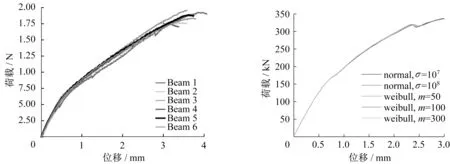
图9 文献［16］与本文荷载-挠度曲线对比Fig.9 The comparison of the load-deflection curve

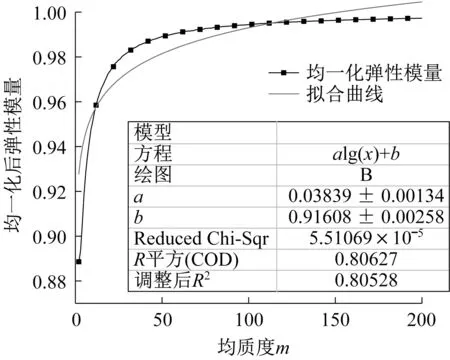
图10 均质度在1～200之间的拟合曲线Fig.10 Fitting curve with homogeneity between 1 and 200

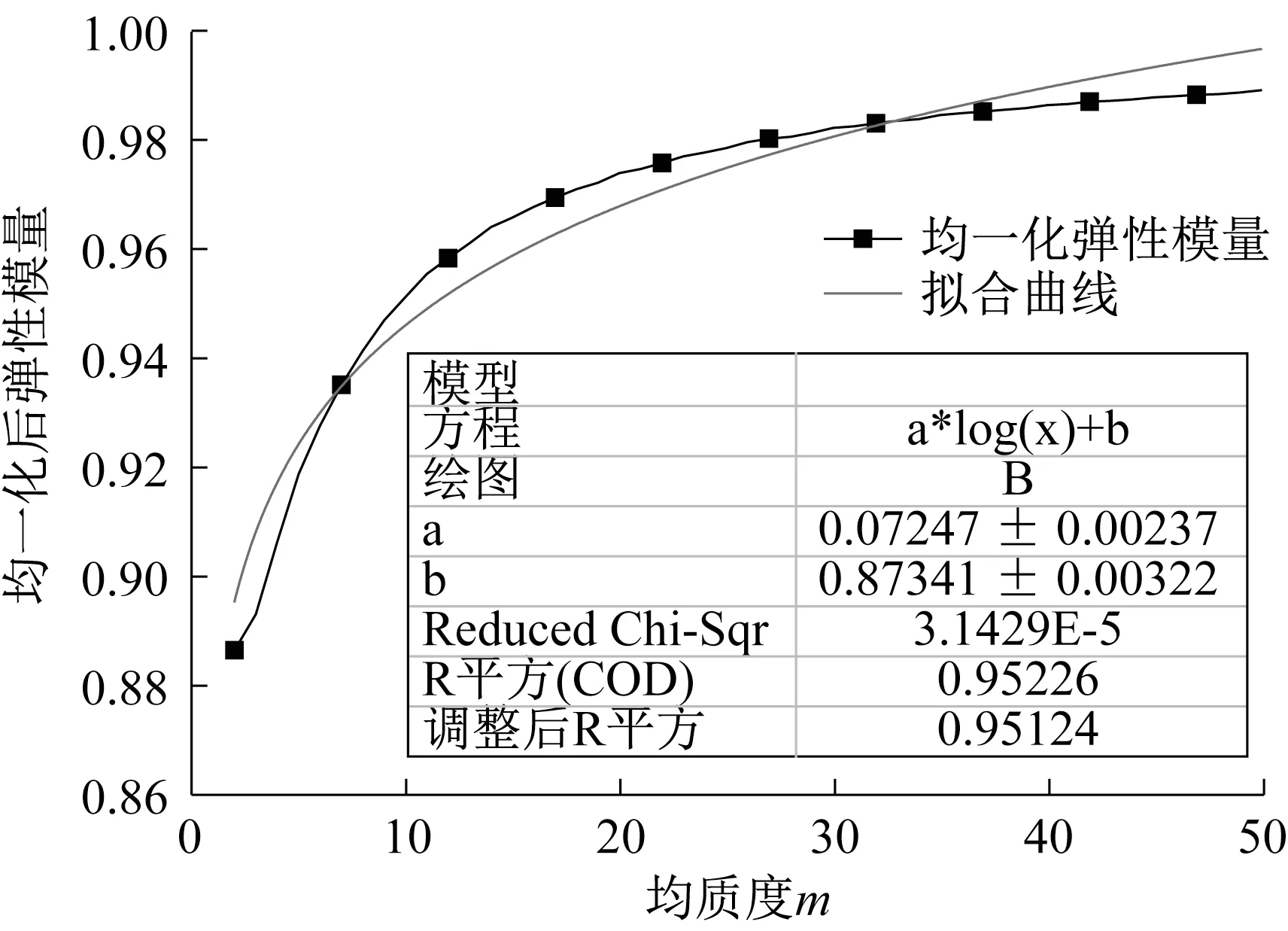
图11 均质度在1～50之间的拟合曲线Fig.11 Fitting curve with homogeneity between 1 and 50

5 结 论

（1）通过ABAQUS 自带的CDP 模型模拟混凝土的塑性损伤，通过三维随机骨料模型模拟混凝土的非均质性可以精确地模拟混凝土的断裂破坏过程。

（2）传统的有限元模型一个单元只有一种材料属性，本文通过PYTHON 语言进行切割合并布尔操作，给不同的骨料赋予不同的材料属性，划分网格后一个单元可能被赋予多种材料属性，可以更大程度地模拟非均质性，比传统方法有较大的改进。本文提出的这种建模方法可以作为模拟非均质性三维建模的一种有效的新方法。

（3）由于混凝土骨料数目巨大且涉及高度非线性运算，采用程序语言循环函数建模可以提高建模效率。对于混凝土非均质性的模拟，将混凝土视为一相非均质材料比视为三相非均质材料节约建模时间，而且通过合理取值可以得到较高的数值精度。

（4）混凝土弹性模量非均质特征包括两方面内容：第一，不同的Weibull 参数必定代表不同的非均质材料；第二，相同的Weibull分布参数，由于数据是随机产生的，材料参数在数值上往往不同。

（5）弹性模量非均质性用正态分布表征时，正态分布的标准差表征非均质度，标准差最合理取值为107～108；弹性模量非均质性用Weibull 分布表征时，均质度最合理取值为50，Weibull 分布比正态分布能更好地表征混凝土弹性模量的非均质性，标准差和均质度取值不合理会导致ABAQUS CDP本构自动检测通不过而无法计算。

（6）混凝土其他材料参数（泊松比、抗压强度、抗拉强度）的非均质性概率密度分布类型将是下一个研究的课题。