宽箱多室组合折腹简支梁桥剪力滞效应分析
2020-11-12王思豪刘玉擎
施 智 王思豪 刘玉擎,*
(1.广西交科集团有限公司,南宁530007;2.同济大学桥梁工程系,上海200092)
0 引 言
近年来,组合折腹桥梁在我国得到积极应用,如国内首座宽箱多室的杭州德胜路高架桥、首座采用无防腐涂装耐候波形钢板的运宝黄河大桥等[1-2]。
与混凝土箱梁类似,组合折腹箱梁顶底板同样会存在剪力滞效应,一直以来是工程界关注的重点。日本相关设计指南[3]不考虑顶底板剪力滞效应,认为混凝土全断面受压。吴文清[4]通过模型试验测量了组合折腹箱梁顶底板正应力分布,基于有限元参数分析研究剪力滞系数的主要影响因素,拟合得到单箱单室组合折腹梁桥剪力滞系数经验公式;李立峰[5]基于变分法推导了单箱单室组合折腹箱梁在集中荷载和均布荷载作用下的计算公式;马磊[6]实测某单箱三室组合折腹梁桥在车辆荷载作用下典型断面的剪力滞系数,结果表明,边腹板剪力滞系数明显大于中腹板,并比较了国内外相关规范有效宽度系数计算方法的适用性;卫星[7]基于实桥三维空间有限元模型,比较了混凝土箱梁和单箱双室组合折腹箱梁桥剪力滞系数的差异,分析了剪力滞系数的影响因素;Ji[8]考虑剪力滞效应和腹板剪变形推导了波形钢腹板简支梁挠度计算公式;Chen[9]提出了新型波折钢腹板-双管弦杆-混凝土板组合梁,基于能量法推导了该种组合梁剪力滞系数计算公式。
目前组合折腹箱梁桥剪力滞的研究主要集中于单箱单室箱梁,宽箱多室的研究相对较少。当前宽箱组合折腹箱梁在城市桥梁得到越来越多的应用,由于腹板数量的增多以及不同腹板剪力分配的不均匀,使得多室箱梁剪力滞分布规律存在较大差异。为此,通过有限元方法研究宽箱三室简支组合折腹箱梁剪力滞变化规律,分析影响剪力滞效应的主要因素,拟合顶底板有效宽度实用计算公式,为宽箱三室组合折腹简支梁桥的设计提供参考。
1 有限元模型
建立某宽箱三室组合折腹简支箱梁有限元模型,拟定的截面尺寸和有限元模型如图1 所示。其中顶底板、横隔板采用8 结点六面体实体单元SOLID65 模拟,波折钢腹板采用4 结点板壳单元SHELL63模拟。
荷载作用于顶板和腹板交界处,其中集中荷载P 取1440 kN,均布荷载集度q 取42 kN/m,计算跨径为23.8 m。混凝土为C50,钢材为Q345,波折钢腹板采用1600 型,上下结合部采用焊钉连接件,其轴向和横向间距均为0.2 m。
顶底板与腹板之间采用翼缘型连接件方式,翼缘板上布置焊钉连接件,焊钉直径22 mm,纵横向间距均为200 cm。焊钉采用弹簧单元来模拟,其抗剪刚度按式(1)进行计算[10],上下翼缘板和顶底板之间建立接触关系。

式中:ks为单个焊钉抗剪刚度;ds为焊钉直径;Es为钢材弹性模量;Ec为混凝土弹性模量。

图1 宽箱三室组合折腹箱梁有限元模型Fig.1 Finite element model of the composite box girder
2 剪力滞效应变化规律分析
2.1 纵桥向变化规律
图2 所示为移动集中荷载作用下翼板剪力滞系数沿纵向的变化规律。其中,x 为纵桥向位置,L 为桥梁跨径。集中荷载剪力滞效应纵向影响区较窄,因受载截面的剪力方向有突变,翼板纵向剪切变形比较严重,剪力滞系数变化显著,荷载作用点靠近支点时,剪力滞系数逐渐增大。
均布荷载作用下,靠近支点时截面剪力滞系数逐渐增加,远离支点截面时剪力滞效应逐渐减小,主要由于简支梁跨中截面剪力趋近于0,而支点截面剪力较大。顶板与内、外腹板交界处的剪力滞系数比较接近,而下翼板与内、外腹板交界处的剪力滞系数差异比较明显,应引起重视。
2.2 横桥向分布规律
图3 所示为单箱三室简支组合折腹箱梁1/4跨截面剪力滞系数横向分布。简支梁1/4 截面发生正剪力滞效应,顶底板和腹板交界处剪力滞效应较为显著;集中荷载下顶板与腹板交界处剪力滞大于均布荷载情况,而顶板跨中剪力滞系数则小于均布荷载;与单箱单室组合折腹箱梁不同的是,宽箱多室底板剪力滞效应较顶板显著,且底板与外腹板交界处剪力滞效应明显大于内腹板。

图2 顶底板剪力滞系数λ纵向分布Fig.2 Longitudinal distribution of shear lag coefficient λ for top and bottom slabs
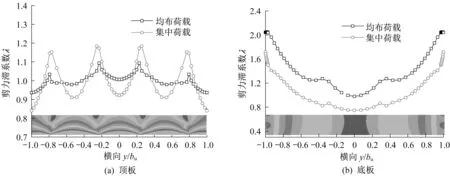
图3 1/4跨截面剪力滞系数λ横向分布Fig.3 Transverse distribution of shear lag coefficient λ for 1/4 midspan
3 剪力滞效应参数分析
3.1 宽跨比
图4 所示为单箱三室组合折腹箱梁剪力滞系数随宽跨比的变化。当宽跨比从0.05 增加至0.25,顶板腹板位置剪力滞系数从1.01 增大至1.37;底板与内、外腹板交界处的剪力滞系数随宽跨比的增大速率并不相同,底板与外腹板的剪力滞系数增加较快,当宽跨比从0.05增加至0.25时,集中荷载作用下其剪力滞系数从1.10 变化至3.06,变化显著。
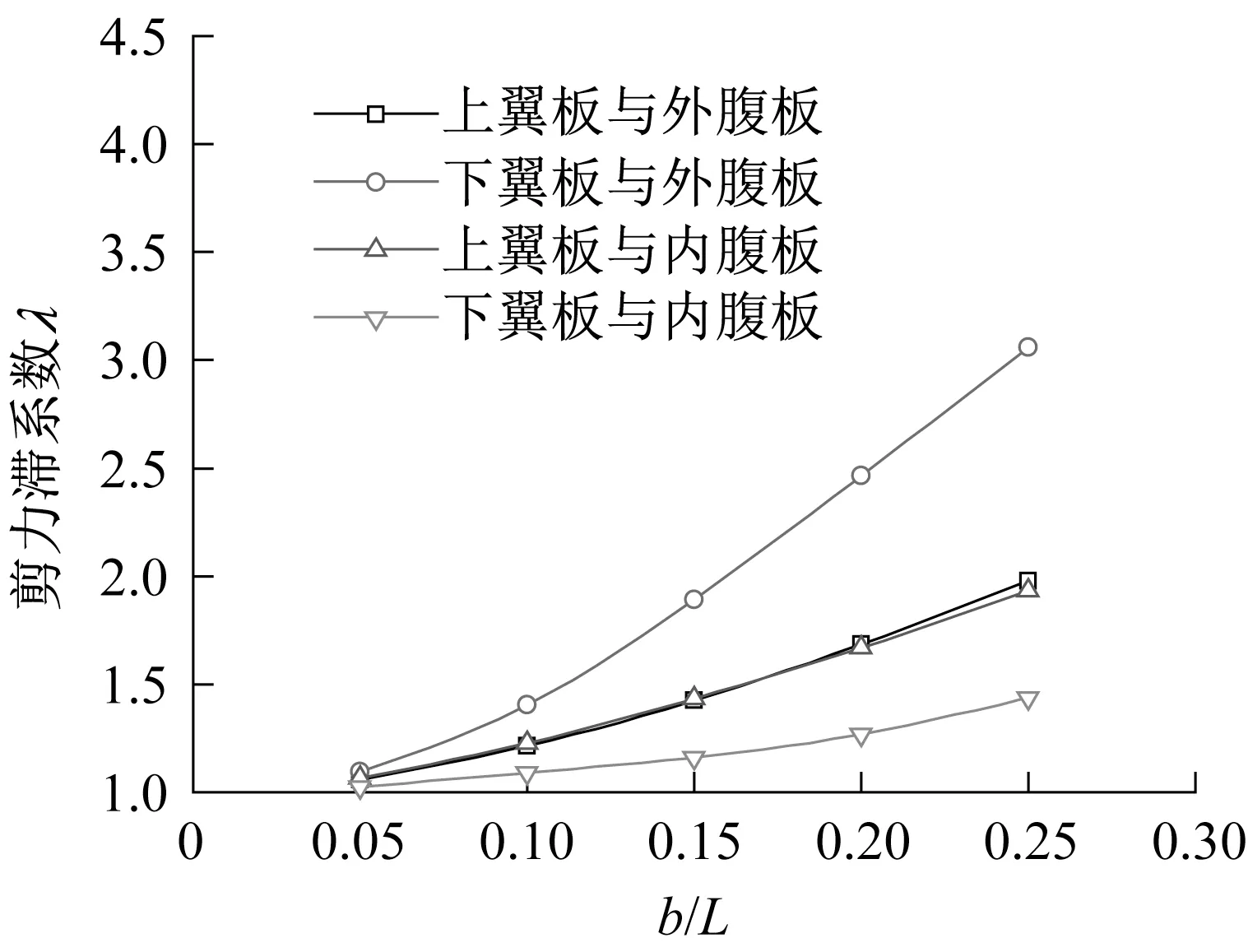
图4 剪力滞系数λ与宽跨比的关系Fig.4 Relationship between λ and width-span ratio
3.2 顶板悬翼比
图5 所示为顶板悬翼比对剪力滞系数的影响。悬翼比对顶板剪力滞效应影响较为明显,而对底板剪力滞效应影响较小,可以忽略不计。当悬翼比为0.5 时,顶板与内、外腹板交界处的剪力滞系数较为接近,且剪力滞系数数值相对较小,正应力分布较为均匀。因此,从减小顶板剪力滞系数差异的角度考虑,建议采用0.5的悬翼比。

图5 剪力滞系数λ与悬翼比的关系Fig.5 Relationship between λ and flange to top slab width ratio
3.3 钢混相对滑移
通过调整单根焊钉的抗剪刚度ks来改变波折钢腹板与顶底板界面单位长度上的抗剪刚度K,从而改变单位长度上相对滑移量s。s可以采用式式(2)进行计算。

式中,ns为同一截面焊钉数量;ks为单个焊钉连接件的抗剪刚度;p 为焊钉纵向间距;V 为单位长度界面剪力;K0=1/mm。
基本模型单位长度相对滑移为s0,参数分析模型中相对滑移取s值范围为0.1 s0~5 s0。
图6 所示为钢混相对滑移s/s0对剪力滞系数的影响。剪力滞系数随s/s0增加逐渐减小并于平稳,当s/s0从0.5 增加至2 时,λ 约减小5.3%。因此,在常用界面抗剪刚度范围内可忽略其对剪力滞系数的影响。

图6 剪力滞系数λ与界面相对滑移关系Fig.6 Relationship between λ and connection relative slip
3.4 内外箱室间距
图7 所示为箱室间距对对剪力滞系数的影响。顶底板与外腹板交界处的剪力滞系数随b2/b1的增大而逐渐减小,当b2/b1>1.0 后,剪力滞系数趋于稳定;当b2/b1≤1.0 时,顶底板与内腹板交界处的剪力滞系数随b2/b1的增大而增大,当b2/b1>1.0 时逐渐减小。总体上,当内外箱室间距b2=b1时,顶底板与内、外腹板交界处的剪力滞系数均较为接近,因此,应尽量采用等腹板间距的单箱三室截面。
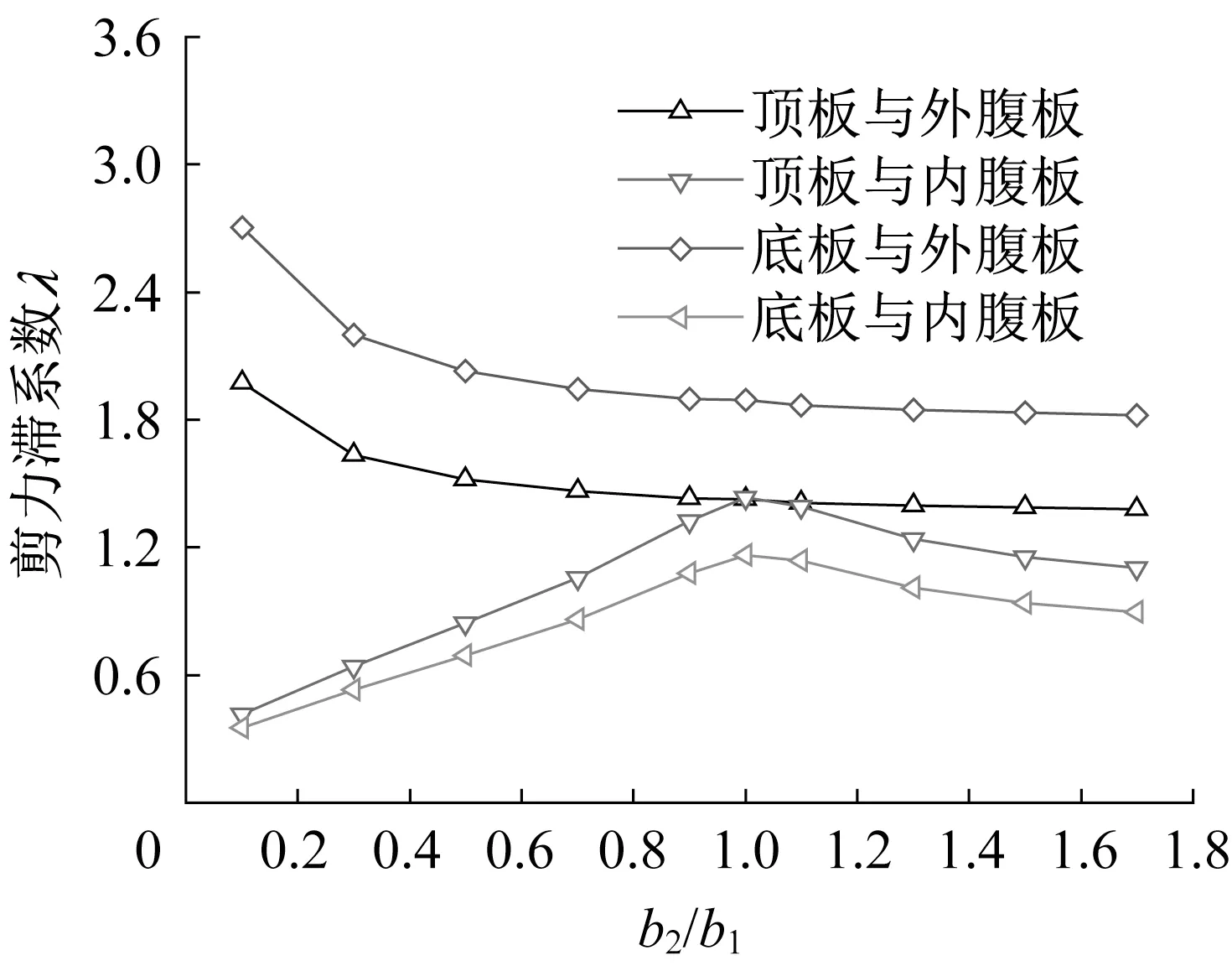
图7 剪力滞系数λ与内外箱室间距关系Fig.7 Relationship between λ and distance between inner and outer cells
3.5 梗肋长度
由于顶板预应力布置空间的限制,不同桥梁梗肋长度一般不同,但倾角一般小于45°。梗肋尺寸如图8所示。顶板梗肋高度hh=0.3 m,考虑到腹板间距的限制,分别取bh:hh等于1~9进行参数分析。
图9 所示为梗肋长度对剪力滞系数的影响。当梗肋高度一定时,顶板与外腹板交界处的剪力滞系数随着梗肋长度的增加而减小,梗肋长度约为梗肋高度的6 倍时,梗肋长度对剪力滞效应的削弱效应逐渐趋于平缓,且梗肋长度变化时剪力滞系数的减小值不超过10%。
3.6 横隔板
图10 所示为横隔板数量对剪力滞系数的影响。横隔板的设置可以有效改善底板与外腹板交界处的剪力滞效应,其改善程度与横隔板数量和箱梁宽跨比有关。当横隔板数量从0增加到3时,剪力滞系数逐渐减小,超过3 道后,剪力滞系数基本保持不变,因此从改善下翼缘与外腹板交界处剪力滞效应的角度看,仅设置跨中1道横隔板即可。

图8 梗肋尺寸Fig.8 Dimensions of the bottom corner

图9 剪力滞系数λ与梗肋长度的关系Fig.9 Relationship between λ and length of the bottom corner

图10 剪力滞系数λ与横隔板数量的关系Fig.10 Relationship between λ and amount of the diagrams
4 有效宽度系数实用计算方法
4.1 宽箱多室有效宽度定义
对于宽箱三室组合折腹箱梁,翼板与内、外腹板交界处应力峰值差异随宽跨比的增大而增加,不能像传统的单箱单室箱梁或者组合钢板梁那样,对腹板两侧的翼板分别定义有效宽度。本文定义如图11 所示的有效截面宽度be,即用顶底板最大峰值应力作为等效应力进行计算。

图11 宽箱三室组合折腹箱梁有效宽度定义Fig.11 Definition of effective width of the three-cell box girder
为综合考虑翼板厚度范围内各层应力分布,本文按下式定义有效宽度be

定义顶底板有效宽度系数η:

η 表示翼板有效参与工作的程度,其值越大表示顶底板工作效率越高。
4.2 有效宽度系数计算
由剪力滞效应纵向分布规律的分析可知,简支梁有效宽度系数沿全跨并非一个常数,但在一般情况下,跨中截面为正应力控制截面。因此,可偏安全取跨中截面的有效宽度系数值作为全跨有效宽度系数。图12所示为宽箱三室简支组合折腹梁顶底板有效宽度系数η随宽跨比b/L的变化。
为便于实际工程设计,以有限元结果为基础,对组合梁有效翼缘宽度随宽跨比变化规律进行回归分析,得到简支梁顶底板集中荷载作用下有效宽度系数:

均布荷载作用下有效宽度系数:
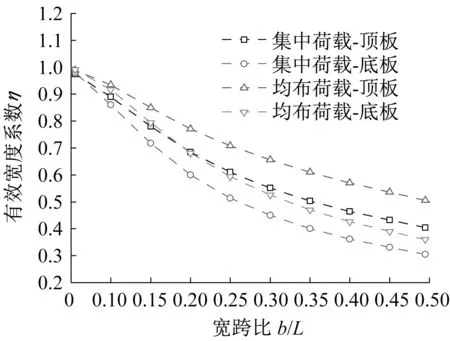
图12 有效宽度系数η与宽跨比关系Fig.12 Relationship between λ and width-span ratio

式(5)-式(8)适用范围为顶板悬翼比接近0.5,截面抗剪刚度足够,内外箱室间距相等、梗肋倾角小于45°、横隔板板数量多于3个的宽箱三室组合折腹箱梁。
5 结 论
(1)宽箱三室组合折腹简支梁集中荷载下剪力滞效应主要分布在加载点位置,均布荷载下支点区段剪力滞系数大于跨中。
(2)宽箱三室组合折腹箱梁顶板内外侧腹板处剪力滞系数一般相差不大,但底板外腹板处剪力滞明显大于内腹板,且底板剪力滞系数一般大于顶板。
(3)随着宽跨比的增大,剪力滞系数逐渐增大;顶板悬翼比采用0.5、内外箱室间距相等时不同腹板处剪力滞系数分布均匀;界面抗剪刚度足够、梗肋长度为高度6倍、横隔板数量大于3时,剪力滞系数基本保持不变。
(4)基于参数拟合和等效跨径的方法得到简支梁有效宽度系数实用计算方法,可用于组合折腹梁桥设计参考。
