中国股市流动性风险研究——基于金融市场微观结构视角

王文胜，刘 倩

(杭州电子科技大学 经济学院，浙江 杭州 310018)

随着全球金融自由化进程的不断推进，各国金融市场的联系日益紧密，但同时金融危机表现出极强的国际传递性，一国金融风暴可能引发全球金融动荡，其波及范围和连带破坏力不容小觑。中国受全球经济的影响，股市跌宕起伏，因此加强金融市场监管，营造良好的金融秩序，进行有效的风险管理具有重要性和紧迫性。

股票的收益率具有典型的波动聚集性和持续性，由Engle(1982)[1]提出的自回归条件异方差模型和Bollerslev(1986)[2]提出的广义自回归条件异方差模型可以很好地描述这种特征。但随着研究的深入，广义自回归条件异方差的改进和拓展模型开始被更多的广大学者关注和使用。

交易量与股价之间的关系，一直以来都是一个重要话题。关于交易量与股价相关性的理论有很多，其中最具代表性的就是混合分布假说理论，该理论认为交易量作为信息代理变量，对收益率具有驱动作用。Andersen(1996)[3]将混合分布假说理论与市场微观结构理论结合起来，建立了修正的混合分布假说理论。Slim和Dahmene(2015)[4]基于修正的混合分布假说模型，对成交量信息进行分解，探究成交量各部分分解信息与波动率的关系。国内学者在价量关系的研究上也取得了较大的成果，陈虹和徐融(2017)[5]建立非对称广义自回归条件异方差模型，证明了成交量具有明显的杠杆效应，对上证综指和深证综指的收益率影响显著。任艳艳和李劭民(2017)[6]认为收益率处于较高分位水平时会正向影响成交量，收益率在较低水平时，二者呈负相关。石建勋等(2017)[7]从不确定性的视角出发，研究分析结构变动对于量价关系的影响，实证结果表明两者具有明显的时间断点效应。

在股票市场中同样不可被忽视的就是价格，收盘价的重要性已经被很多学者所证明，为使各种类型的价格信息更充分地被运用到风险度量中，Parkinson(1980)[8]提出在某个时间段内，金融资产价格的最高价减去最低价的极差，是衡量价格波动的良好指标。该研究成果促使各位学者在研究金融资产时，开始关注价格极差的影响作用。Hansen和Zhou(2016)[9]建立波动率和价格极差的多重测度组合模型，经过检验分析得出，这一组合模型的拟合效果要优于单一测度模型。刘威仪等(2016)[10]借助对上证指数的实证分析，证明了最高价与最低价的有效价差可以有效提高波动率和风险价值的预测。岳婷婷(2019)[11]引入价格极差这一测度，构建波动率的估计模型，明显改善了波动模型对风险的刻画效果。

风险管理的关键在于准确的金融风险度量，Bangia等(2001)[12]提出了流动风险模型，模型从相对价差出发，可分解为内生性风险和外生性风险两个部分，有效解决了传统风险模型设定不存在市场摩擦的局限。国内在这方面的研究虽起步较晚，但工作成果颇丰。胡晖和王琰(2009)[13]对流动风险模型进行了调整，将相对价差改为最高价与最低价之间的价差，并通过实证检验验证了该模型符合我国A股市场行情。胡方琦和宋琴(2015)[14]通过上证国债指数分析我国国债市场流动性风险的测度问题，结果表明流动风险模型要优于传统风险价值模型，预测结果与实际市场大致吻合。张亚西(2016)[15]从市场宽度、深度以及价量综合三个层面构建流动性指标因子，据此分析新三板市场的流动性特点，以实现风险值的准确预算。

目前关于流动风险的研究，大多以收盘价作为度量因素对股票收益率的波动情况进行测算，忽视了反映股票市场交易量、日交易价格波动程度等重要信息。为了对流动风险进行更精准地刻画，文章在已有研究基础上，将价格极差和交易量加入到传统的广义自回归条件异方差模型当中，为探究股票市场中的金融波动以及风险度量问题，增强金融市场的弹性和韧性，维护金融市场的稳定，促进我国金融市场的健康发展提供针对性建议。

一、模型构建

(一)价格极差-交易量-广义自回归条件异方差模型的构建

本文以广义自回归条件异方差模型为基准，引入价格极差和交易量构建价格极差-交易量-广义自回归条件异方差改进模型。

模型可表示为：

rt=ut+εt

(1)

(2)

其中，rt为股票收益率，Wt为价格极差，Vt为交易量，ζ≥0，γ≥0分别表示价格极差和交易量因子对收益率的影响程度。当ζ=γ=0时，模型(1)和(2)代表传统的广义自回归条件异方差模型。

GARCH(1,1)中，α1与α2和的大小表现了股价波动程度，二者的系数和越接近1，表示波动性越强；系数和越接近0，表示波动性的持续性越弱。不同波动因子的信息代理能力主要体现在以下两个方面(以交易量为例)：(1)对于波动性的持续解释能力：如果加入交易量后，波动性的持续效应变弱，说明交易量对波动性的持续解释能力越强，这体现在α1+α2的值显著变小。(2)对波动性的边际解释能力：如果γ的值越大，那么就表示波动性能够较好地被交易量所解释。同理，当引入价格极差后，如果α1+α2的值显著减小，并且ζ显著为正时，表示波动率能很好地为价格极差所解释。

(二)风险度量模型的构建

假定金融资产当日最高价、最低价分别为P1和P2，中间价格St=(P1+P2)/2，S和rs分别为绝对价差和相对价差，可表示为S=P1-P2，rs=S/Pt，则在置信水平α下，头寸为一单位的金融资产在未来某个持有期的风险值La-VaR的解析式为：

(3)

等式右边的第一项表示市场价格风险，第二项表示价差流动风险。其中，在价格风险部分，μ表示收益率的期望，σt表示收益率的标准差，zα表示收益率的α分位数。修正因子θ是针对收益率的尖峰厚尾特征调整的参数因子，它可以用一个经验函数来估计：

θ=1+φln(k/3)

二、股票市场风险度量的实证研究

(一)数据来源及基本分析

文章选用与股市行情数据变化一致的上证指数为研究对象，数据选取具有以下特点：(1)所选数据应满足研究分析的一般性要求，因2007年至2009年世界性的金融危机造成股市行情萎靡，资产价格大幅下跌，故选取2011年1月4日至2019年4月30日的数据。(2)所选取的指标有：股票收盘价、交易量、最高最低价等信息。(3)数据来源于RESSET数据库。

建模分析前，对数据首先进行如下处理：

rt=100*ln(Pt/Pt-1)，Wt=100*ln(Pt,max/Pt,min)，Vt=100*ln(Vt/Vt-1)

其中，Pt为当日收盘价，Vt为当日交易量，Pt,max为当日最高价，Pt,min为当日最低价。

表1 数据的基本分析

表1是上证指数收益率、价格极差、交易量的描述性统计结果，从峰度和偏度系数可以看出，三个指标变量的峰度值均大于正态分布标准值3，偏度值均不为0，表现出明显的“尖峰有偏”特征，并且J-B统计量在1%的显著性水平下显著拒绝三个序列服从正态分布的假说。此外，平稳性检验的t统计量在1%的水平下是显著的，说明序列均为平稳序列。残差平方Q统计量在1%显著性水平下也表现显著，对应伴随概率为0，表明三个变量的残差序列均存在条件异方差性。

综上所述，广义自回归条件异方差模型能够从异方差性、波动持续性等方面对收益率、价格极差和交易量序列进行刻画，实现模型参数的有效估计。

(二)价格极差-交易量-广义自回归条件异方差模型的参数估计

通过AIC、BIC准则选择滞后阶数为(1,1)的广义自回归条件异方差模型，分别在正态分布、t分布、GED分布下对传统模型和改进模型进行参数估计和拟合预测。

表2 传统模型与改进模型参数估计结果

从表2可以看出，传统模型下，样本系数大多在1%的水平下通过了检验(只有个别为5%)，表现十分显著，α1和α2的和非常接近1(计算值多为0.99左右)，收益率波动非常剧烈，表明广义自回归条件异方差模型对于价格波动的拟合与真实的波动情况具有契合一致性。

而对于价格极差-交易量-广义自回归条件异方差改进模型，α1和α2的和明显减小，响应变量的系数估计量均为正值，同时，两个响应变量的引入导致AIC显著减小。说明交易量和价格极差的引入，能明显降低广义自回归条件异方差效应的解释能力，收益率的波动变化能够通过价格极差和交易量两个代理变量得到良好的解释。一定程度上也反映了价格极差和交易量可以内在揭示股票的很多信息，对其进一步挖掘分析，可能会解释更多关于股市的现象。

(三)风险度量结果分析

根据参数模拟结果，在三种分布下分别度量股市的流动风险值(在置信度95%的水平下)，度量结果见图1-图3。

图1 改进模型下的风险度量(正态分布)

图2 改进模型下的风险度量(t分布)

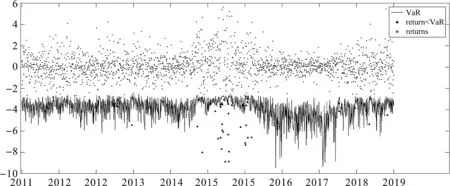
图3 改进模型下的风险度量(GED分布)

由图1-图3可知，价格极差-交易量-广义自回归条件异方差模型计算出的风险值与收益率的走势趋势一致，并且基本能够覆盖收益率的点分布，同时流动风险的值大多都在收益率的下方，只有少数溢出点(三角标志)，这说明改进后的模型能够充分估计出股票的流动风险，正确率较高。

为准确度量模型的有效程度，本文将通过Kupiec方法进行回测检验。回测检验的样本选取为2015年1月19日至2017年2月23日，数据总个数T=510，回测检验的思路为：作风险值与真实值的差值，记为a，若a<0，即风险值小于真实值，则定义失败，计算所有的失败天数，与表3对应的失败区间做对比。此外，失败天数与数据总个数T的比值代表失败率，失败率越靠近5%(显著性水平)，模型拟合预测效果越好。

表3 失败天数接受区间

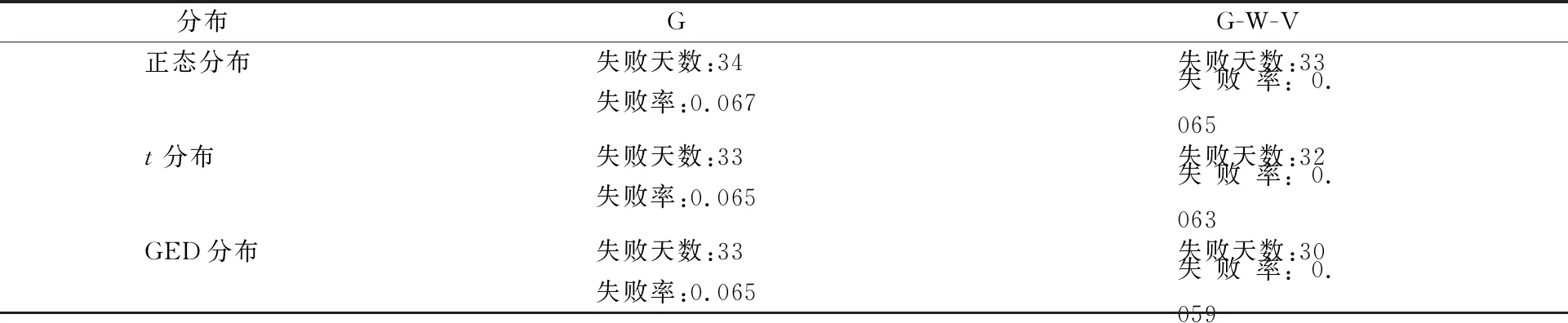
表4 95%置信水平下改进模型与传统模型的回测结果

在95%的置信水平，样本个数为510的情形下，失败天数的接受区间为[16,36]。表4回测结果显示，传统模型与改进模型对应的失败天数都在可接受域内，表明广义自回归条件异方差模型能够有效地对风险进行刻画。此外，横向水平来看，在三种分布下改进的广义自回归条件异方差模型失败率均小于未改进的广义自回归条件异方差模型，并且越来越接近显著性水平5%，这说明改进后模型的拟合效果更优越，稳健性更高。同时，纵向水平来看，t分布、GED分布在两种模型下对应的失败率均低于正态分布，这也再次验证了收益率序列不符合正态性检验的结论，而t分布和GED分布更符合数据分布的性质特点。

三、结论与建议

(一)研究结论

本文在经典流动风险模型的基础上，基于广义自回归条件异方差模型，增加股票日交易量及最高价与最低价之间的价差为信息代理变量。结果表明：改进的价格极差-交易量-广义自回归条件异方差模型在收益率波动测度上解释效果表现良好，信息代理变量可以在很大程度上降低股票收益率波动的持续性。此外，返回测验结果表明：改进后的模型不仅具有良好的覆盖能力，与上证指数实际的收益率波动走势相吻合，而且对于风险测度的错误率更低，风险刻画更加准确。这不仅为测量风险提供了一个很好的思路，也从另一个侧面反映了要对风险进行更全面、更综合、更有效的管理。

(二)建议

首先，相关政府监管者需要制定合理的监管机制，对股票市场进行有效地管理，引导投资者进行理性地投资，从而在一定程度上减少金融市场从众、盲目的行为等，缓解羊群效应。

其次，市场监管者应适当调整交易机制，以降低流动风险。涨跌停限制会引起流动风险的明显变化，因此可以调整涨跌停机制降低风险。

同时，金融市场参与者应加强对流动风险的认识。流动性作为金融市场的生命力所在，对整个市场的发展发挥着重要作用。因此，要高度重视流动性风险的有效测量，提高风险预警能力。

最后，应加强整个风险体系系统的构建。风险模型应结合市场的变化，不断改进和完善，从而适应金融市场的快速变革，为构建更稳定有效的风险管理体系，提高金融机构抗风险的能力，促进市场的平稳运行不断发挥作用。