车用钢板材料硬化模型的适用性

董伊康，齐建军，孙 力，罗 扬，王 健，杨 婷，邢承亮

(河钢集团钢研总院，石家庄 050023)

0 引 言

随着汽车工业的快速发展，汽车产品的生命周期变得越来越短，新产品的开发周期成为衡量其竞争力的重要指标，并且虚拟仿真技术在汽车设计开发过程中也起着越来越重要的作用。冲压同步工程是新车型开发中的重要环节，可有效降低研发成本，缩短开发周期。精准的材料特性能够显著提高数值仿真的精度。对于冲压成形仿真研究，材料硬化曲线对准确预测材料冲压及回弹行为非常重要。但是，由拉伸试验得到的流动应力范围达不到冲压成形数值仿真的需求，需要基于硬化模型对塑性应力-应变曲线进行外推以获取更大范围的流动应力。常见的硬化模型包括Ludwik、Swift、Hockett-Sherby、Voce等[1-2]，相关的金属材料力学性能及力学模型表征方法很多[3-5]。CAPILLA等[6]采用金属板拉伸弯曲测试装置结合有限元仿真分析，确定了4种高强钢的Swift-Voce混合硬化模型加权系数，并预测了大变形下的流动应力。PAUL等[7]利用数字图像相关法(DIC)得到颈缩后钢板的真实拉伸应力-应变曲线，比较了不同硬化模型对大变形应力、应变的预测能力。刘国承等[8]以DX56D+Z冷轧镀锌板为例，研究了各向异性材料的等效塑性应变表达式，并对大应变条件下的材料流动应力进行建模与预测。崔伟强等[9]采用试验与仿真相结合的方法，对比了不同硬化模型的差异，确定了与某合金钢材料最为匹配的硬化模型的加权系数，并采用线弹塑性本构模型进行有限元仿真分析，验证了材料模型的准确性。ZHAO等[10]通过单向拉伸试验和有限元仿真获得了金属板料在大应变区间内的流动应力曲线，建立了多个不同的硬化模型对该曲线进行描述，并比较了不同模型的拟合效果。

流动应力曲线作为板料成型分析必不可少的输入项，其准确性直接影响仿真精度。因此，选择合适的硬化模型来描述材料在冲压变形过程中的流变特性，对提高板料冲压成形仿真精度具有重要意义。目前，研究多局限于采用不同的硬化模型对单一材料进行分析或者采用单一硬化模型分析多种材料，而采用不同硬化模型对多种材料进行的综合分析较少。因此，作者选取汽车常用的DX56D+Z、HC220BD+Z、HC420LA、HC420/780DP等4种钢板，通过单向拉伸试验获取应力、应变数据，采用不同硬化模型对数据进行拟合，分析不同硬化模型的拟合精度，以期为冲压成形数值仿真提供参考。

1 试验方法与结果

1.1 试验材料

选取河钢集团生产的4种车用钢板作为试验材料，牌号分别为DX56D+Z、HC220BD+Z、HC420LA、HC420/780DP，主要化学成分见表1。

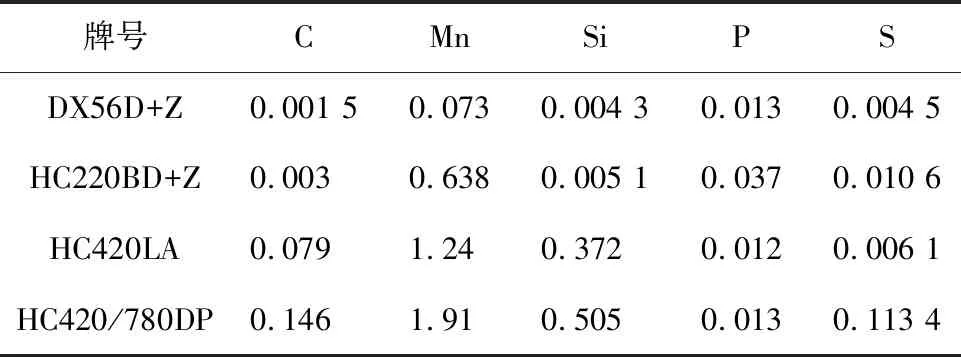
表1 试验钢的主要化学成分(质量分数)

DX56D+Z钢属于无间隙原子钢(IF钢)，通过在超低碳、氮的成分基础上，加入一定量的钛、铌等强碳、氮化合物形成元素，将碳、氮等间隙原子完全固定为碳、氮化合物，从而得到无间隙原子的纯净铁素体组织，如图1(a)所示；该钢主要用于汽车内、外覆盖件,仪表板等对深冲性要求较高的零部件。HC220BD+Z钢属于烘烤硬化钢(BH钢)，其强化机理为在涂装烘烤时热能的作用下利用残留在钢中的固溶碳将冲压成形时导入的位错固定，其组织主要为铁素体，如图1(b)所示；该钢是车身覆盖件轻量>化设计的首选材料。HC420LA钢是最常见的工程用低合金高强度钢，其在复合添加铌、钒、钛的基础上，添加硅、锰等固溶元素来提高强度；该钢具有细小的铁素体+珠光体晶粒组织，如图1(c)所示，主要用于车身结构件。HC420/780DP钢是以相变强化为基础的一种先进高强钢，其显微组织由塑性较好的铁素体基体和弥散分布的岛状马氏体组成，如图1(d)所示；该钢具有屈强比低、初始加工硬化速率高、强度和塑性良好等优点，大量应用于车身结构件和加强件[11-12]。

1.2 试验方法

按照GB/T 228.1-2010，在试验钢上加工出标距为80 mm的矩形拉伸试样，加工方向与轧制方向一致。在Zwick/Roell 100 kN电子拉伸试验机上进行单向拉伸试验，采用应变速率控制模式，应变速率为0.000 25 s-1，利用试验机配置的全自动引伸计测定应变，各测3个平行试样。

1.3 试验结果

有限元仿真时要求的塑性硬化曲线为真应力-塑性应变曲线。真应力和塑性应变的计算公式为

σT=σE(1+εE)

(1)

εpl=εT-σT/E=ln(1+εE)-σT/E

(2)

式中：σE，εE分别为工程应力和工程应变；σT，εT分别为真应力和真应变；εpl为塑性应变；E为弹性模量。

试验测得4种试验钢的工程应力-应变曲线见图2(a)，将屈服点至颈缩点间的工程应力、工程应变代入式(1)和式(2)，得到的真应力-塑性应变曲线见图2(b)。

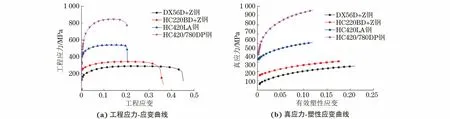
图2 4种试验钢的工程应力-应变和真应力-塑性应变曲线Fig.2 Engineering stress-strain (a) and true stress-plastic strain (b) curves of four test steels

2 常用硬化模型介绍

建立合理的材料塑性变形本构关系对提高板材冲压仿真精度有重要的影响。随着应变增大，Ludwik、Swift、Hockett-Sherby、Voce等硬化模型预测得到的流动应力的差异逐渐增大。根据应力有无上限，可将硬化模型分为饱和模型和非饱和模型。Ludwik硬化模型属于非饱和模型，必经过屈服点且应力无上限，其表达式为

(3)

式中：σ为流动应力，当εpl=0时，σ=σ0(屈服强度)；n为加工硬化指数，n>0；K为材料常数，K>0。

Swift硬化模型也属于非饱和模型，与Ludwik硬化模型不同的是，该模型无初值，其表达式为

σ=C(εpl+ε0)m

(4)

式中：ε0为屈服强度点对应的塑性应变，即屈服应变；m为加工硬化系数，m>0；C为材料常数，C>0。

Hockett-Sherby和Voce硬化模型均属于饱和模型，即随着应变的增大，拟合所得流动应力趋于定值。Hockett-Sherby硬化模型的表达式为

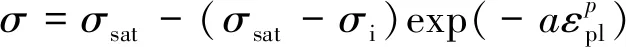
(5)

式中：σsat为饱和应力；σi为初始屈服应力；a，p为常数，a>0。

Voce硬化模型经过屈服点，其表达式为

σ=σ0+A[1-exp(-cεpl)]

(6)

式中：A，c为材料常数，A>0，c>0。

除了上述饱和模型和非饱和模型外，还有一种将饱和项和非饱和项进行叠加构成的非饱和混合模型。常见的混合模型有Swift-Hockett-Sherby硬化模型和Swift-Voce硬化模型。这2种混合模型分别引入权重系数α和ω，通过调整权重系数来控制流动应力的增长趋势。Swift-Hockett-Sherby硬化模型表达式为

σ=(1-α)[C(εpl+ε0)m]+

(7)

Swift-Voce硬化模型表达式为

σ=(1-ω)[C(εpl+ε0)m]+

ω{σ0+A[1-exp(-cεpl)]}

(8)

3 硬化模型适用性分析

3.1 拟合结果

采用上述6种硬化模型对图2中的真应力-塑性应变数据进行拟合，拟合结果见图3，拟合相关系数见表2。由图3可以看出：在塑性变形初期(塑性应变在0～0.075范围内)，Ludwik和Swift硬化模型拟合得到的流动应力与实测数据点之间的误差比其他4种硬化模型的大。对于DX56D+Z钢板，当塑性应变在0.10～0.15之间时，6种硬化模型拟合得到的流动应力与实测数据的重合度均较高；在颈缩前(塑性应变在0.20～0.22之间)，Hockett-Sherby硬化模型和Swift-Voce混合硬化模型的拟合结果几乎和实测数据重合，但Voce和Swift硬化模型的拟合结果偏离实测数据较大。这是因为Swift硬化模型是非饱和模型，其拟合流动应力随着应变的增加会持续快速增大，最终远超实际应力；Voce硬化模型是饱和模型，其拟合流动应力随着应变的增加会趋近于抗拉强度但低于实际应力。对于HC220BD+Z钢板，当塑性应变在0.09～0.14之间时，6种硬化模型拟合出的流动应力与实测数据的重合度均较高；在颈缩前(塑性应变在0.17～0.18之间)，Hockett-Sherby硬化模型拟合结果与实测数据重合度最高，Ludwik硬化模型拟合结果则偏离实测数据较大，Swift-Hockett-Sherby和Swift-Voce混合硬化模型的拟合精度相差不大。对于HC420LA钢，在颈缩前(塑性应变在0.11～0.12之间)，Hockett-Sherby硬化模型拟合结果与实测数据的重合度最高，Ludwik和Swift硬化模型的拟合结果则偏离实测数据较远，Voce硬化模型、Swift-Hockett-Sherby混合模型和Swift-Voce混合模型的拟合精度相差不大，其中Voce硬化模型拟合得到的流动应力基本达到饱和状态。对于HC420/780DP钢板，在颈缩前(塑性应变在0.11～0.12之间)，Hockett-Sherby硬化模型和Swift-Hockett-Sherby混合模型拟合得到的流动应力与实测数据最为接近，Swift和Voce模型拟合结果偏离实测数据最远；Swift和Ludwik非饱和硬化模型拟合得到的流动应力随应变的增加逐渐增大，并且Swift硬化模型的流动应力增加速率高于Ludwik硬化模型的；Voce饱和硬化模型拟合得到的流动应力在塑性应变为0.1时基本达到饱和状态，Hockett-Sherby饱和硬化模型拟合得到的流动应力饱和速率低于Voce饱和硬化模型的。

图3 不同硬化模型拟合得到不同试验钢的流动应力-塑性应变曲线Fig.3 Flow stress-plastic strain curves of different test steels by fitting with different hardening models: (a) DX56D+Z steel; (b) HC220BD+Z steel; (c) HC420LA steel and (d) HC420/780DP steel

由表2可以看出，6种硬化模型的拟合相关系数R2均高于0.98，说明6种硬化模型在一定程度上都可以描述材料在塑性变形段的流动应力。其中，Hockett-Sherby硬化模型、Swift-Hockett-Sherby混合硬化模型和Swift-Voce混合硬化模型的拟合精度较高，适用于4种试验钢，尤其是Hockett-Sherby模型，其描述的流动应力增长趋势与实际最为接近。

表2 不同硬化模型拟合不同试验钢流动应力-塑性应变时的拟合相关系数Table 2 Fitting correlation coefficients of different hardening models when fitting flow stress-plastic strain of different test steels

3.2 大应变范围的适用性分析

以HC420/780DP钢为例进行大应变范围内不同硬化模型的适用性分析。由拉伸试验测得HC420/780DP钢的最大塑性应变为0.12。利用上述6种硬化模型对HC420/780DP钢在塑性应变段的流动应力进行拟合，得到各模型的拟合参数。其中：Ludwik硬化模型中的σ0为483.53 MPa，n和K分别为0.17，1 393.4；Swift硬化模型中的C为1 480.34，ε0为0.002 2，m为0.196；Hockett-Sherby模型中的σsat为1 601.3 MPa，σi为43.78 MPa，a为1.5，p为0.247；Voce模型中的σ0为483.53 MPa，A为458.14，c为33.69。其他2种混合模型的拟合参数见表3。

表3 2种混合模型拟合HC420/780DP钢流动应力-塑性应变所得拟合参数Table 3 Fitting parameters obtained by fitting flow stress-plastic strain of HC420/780DP steel with two mixed hardening models

将拟合参数代入不同硬化模型，建立HC420/780DP钢的硬化模型。采用建立的硬化模型将该钢的流动应力-塑性应变曲线外推至塑性应变为1.00，得到大应变范围的流动应力-塑性应变曲线，如图4所示。

由图4可以看出，6种硬化模型在小应变范围内得到的流动应力-塑性应变曲线差别不大，但由于各个硬化模型在均匀变形阶段的拟合精度及硬化程度存在差异，在经过颈缩点之后拟合得到的流动应力差异增大，且随着应变的增加越来越大。采用Swift非饱和硬化模型拟合得到的流动应力的增长趋势强于采用Ludwik硬化模型拟合得到的，因此Swift硬化模型在变形后期对流动应力的预测值过高。Voce饱和硬化模型拟合得到的流动应力的饱和速率远高于Hockett-Sherby硬化模型拟合得到的，在颈缩点附近就已达到饱和，与抗拉强度相差不大，因此在变形后期对流动应力的预测严重不足。相比于Voce硬化模型，Hockett-Sherby硬化模型中增加了表征加工硬化的常数p来减缓饱和速率，提升饱和流变应力。此外，通过调整混合模型中的权重因子可以提高混合模型对大应变范围内流动应力预测的自由度，更加准确地描述流动应力的真实增长趋势，其中Swift-Voce混合模型的拟合自由度比Swift-Hockett-Sherby混合模型的高。

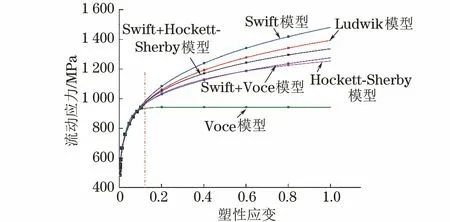
图4 不同硬化模型外推得到HC420/780DP钢在大应变范围内 的流动应力-塑性应变曲线Fig.4 Flow stress-plastic strain curves of HC420/780DP steel in large strain range by extrapolation of different hardening models

目前，各大主机厂均采用主流冲压软件Autoform进行冲压分析[13]。Autoform软件中内嵌了文中所研究的Ludwik、Swift、Hockett-Sherby和Swift-Hockett-Sherby硬化模型。结合以上分析，建议在材料卡片制作时，首选基于材料单向拉伸试验结果建立的Swift-Hockett-Sherby混合硬化模型，确定合适的权重因子，以保证流动应力-塑性应变曲线的拟合精度。

4 结 论

(1) 采用Ludwik、Swift、Hockett-Sherby、Voce、Swift-Hockett-Sherby、Swift-Voce硬化模型对DX56D+Z、HC220BD+Z、HC420LA、HC420/780DP等4种常用汽车钢板进行塑性变形阶段流动应力的拟合，6种硬化模型在小应变范围内的拟合相关系数均高于0.98，说明6种硬化模型在一定程度上都可以描述这4种材料在塑性变形段的流动应力。其中，Hockett-Sherby硬化模型、Swift-Hockett-Sherby混合硬化模型和Swift-Voce混合硬化模型的拟合精度较高，尤其是Hockett-Sherby模型，其描述的流动应力增长趋势与实际最为接近。

(2) 采用6种硬化模型外推得到HC420/780DP钢在大应变范围(过颈缩点)内的流动应力的差异较大，通过调节混合模型中的权重因子可以提高大应变范围内流动应力的拟合自由度。