边赋权图对策Myerson值的和分解

单而芳，刘 珍

(上海大学 管理学院，上海 200444)

0 引言

可转移效用合作对策，也称为TU-对策[1]，描述的是所有参与者通过联盟进行合作并获得收益以及如何分配他们共同的收益[2]。通常假定所有参与者彼此之间都可以进行合作，也就是所有可能的联盟都是可行的。然而在实际中，由于受到各种因素的制约导致有些联盟是无法形成的。为了描述这一事实，Myerson[3]提出了由图作为限制结构的合作对策，图中的点(node)表示参与者，而边(link)表示与该边关联的两个点代表的参与者之间的直接通讯或交流关系，并且假定有边直接相连或通过路(path)相连的参与者之间才能形成联盟进行合作。在这种假定下，Myerson定义了图限制对策(graph-restricted game)[3]并把图限制对策的Shapley值[4]作为分配规则，也即著名的Myerson值。Myerson值可以由分支有效性(component efficiency)和公平性(fairness)所唯一刻画。随后， Myerson[5]又用平衡贡献性(balanced contributions)替代公平性, 给出了Myerson值的另一个刻画。而后，Myerson值被广泛研究，它被推广到一些其他图结构上，例如，超图[6]、概率图[7]、有向图[8]以及边赋权图[9]上。

2003年，Gómez[10]等在研究网络中心性度量时，首次在对称对策上提出了Myerson值的和分解问题。2017年，González[11]等把Myerson值的和分解问题推广到一般图对策上，考虑到每个参与者既可以在他所参与的联盟中获利，又可以作为其他参与者的中介获利，定义了两种分配规则，即组内Myerson值和组间Myerson值，研究了两类Myerson值的性质并给出了刻画。

边赋权图在实际中具有重要的应用，它由点集和边集所组成，其中每条边赋予一个权重(非负实数)，边的权可以用不同的解释：例如：它可以表示通信信道的容量或能力，流经信道的流量，建立或维护通信链路的成本；社会网络中的参与者的亲密度，合作的强度或接触的频率；还可以表示两个点之间的距离等。González-Arangüena等[9]研究了边赋权图的Myerson值问题。

本文继续对Myerson值的和分解问题进行讨论。我们将Myerson值的和分解概念进一步推广到边赋权图对策上，给出了边赋权图上组内Myerson值和组间Myerson值的定义，证明了这两类值可以利用可加性、无效参与者性和关键参与者性所唯一刻画。我们侧重分析了这两类值的稳定性。在某种意义下，证明了边赋权图对策的组内Myerson值和组间Myerson值满足权稳定性和广义稳定性。

本文第一节给出所需要的一些基本定义和记号。第二节提出赋权图对策的Myerson值和分解概念，定义了赋权图对策的组内Myerson值和组间Myerson值并给出刻画。第三节以边权表示边的通讯容量为例，讨论了赋权图对策组内Myerson值和组间Myerson值的权稳定性和广义稳定性。第四节对本文工作进行了总结。

1 预备知识

1.1 TU-对策

可转移效用合作对策，又叫做TU-对策[1]，用二元组(N,v)来表示，其中N= {1,2,…n}，表示参与者(player)的集合，v表示特征函数(characteristic function)，是定义在2N上的实数映射，并且满足v(Ø)=0。对于每个联盟(coalition)S⊆N，v(S)表示S中的参与者同意合作所得的效用(utility)。记GN为参与者集合N上的所有对策的集。

对于每个非空联盟S⊆N，一致性对策(N,uT)的特征函数可以表示为: 若T⊆S，则uT(S)=1，否则uT(S)=0。已经知道GN中的任意对策的特征函数都可以用一致性对策的线性组合来唯一表示, 也即:

(1)

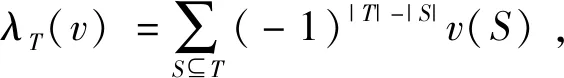
在TU-对策中，最重要有效分配方案是由Shapley在1953年提出的，即著名的Shapley值[4]，它可以表示为:

(2)

这里|S|=s,|N|=n。

1.2 图、图对策和Myerson值

一个图可以用二元组(N,v)表示。其中N={1,2,…,n}表示点的集合，L表示边的集合，即L⊆{{i,j}|i,j∈N,i≠j}。通常用i,j替代{i,j}表示L的一条边,而以L来表示图(N,L)，并记Li={ij∈L:j∈N}，也即L中与点i关联的边的集。

对于图L，如果ij∈L，则说点i和j在图中是直接连通的。互异点列i1,i2,…,ik称为图L的一条路，如果对于任意的h=1,…,k-1，都有ihih+1∈L。如果两个点i,j之间存在一条路，则说i和j是连通的。若(N,L)中任意两个点都是连通的，则称(N,L)是连通的。对于非空点集S∈N，L(S)称为由点集S导出的子图，并且L(S)={ij∈L:i,j∈S}。如果子图(S,L(S) )是连通的，则称S是连通子集。图L的极大连通子图称为分支。记L中所有连通分支的集为N/L。类似地，记S/L为L(S)所有分支的集。对L(S)和i∈N，分别用L{l}和L-i表示去掉边L和去掉与i相关联的所有边所形成的生成子图。

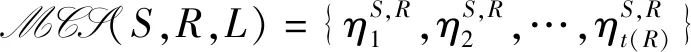
1.3 边赋权图对策的Myerson值

一个边赋权图用二元组(N,Lw)表示。其中N是点集，而Lw={L,{wl}l∈L}，wl≥0。边赋权图中边的权wl可以有多种不同的解释，例如：wl可以表示边l的通讯容量(capacity)，此时，wl∈(0,1]。wl可以表示l的两个端点所代表的参与者之间的距离(distance)或是建立和维持合作关系所需的成本(cost)，此时，wl∈[0,∞)。更多含义的解释可参见[9]。本文以边权代表边的通讯容量为例进行讨论，其他情况可做类似处理。

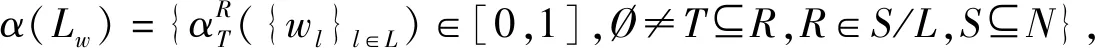
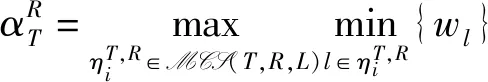
(3)

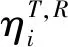
(4)

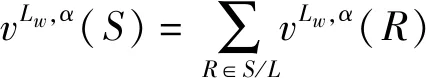
此时, 边赋权图限制对策与图限制对策是一致的。

González用分支有效性、公平性和平衡贡献性对赋权图对策Myerson值进行了刻画。

2 边赋权图对策组内Myerson值和组间Myerson值

2017年，González[11]把图对策的Myerson值分解为组内Myerson值和组间Myerson值的和，以此来区分每个参与者在参与联盟中所获收益和他作为其他参与者的中介所获得的收益。本节将把图对策Myerson值的和分解概念推广到边赋权图对策上，定义边赋权图对策组内Myerson值和组间Myerson值并给出刻画。

2.1 边赋权图对策组内Myerson值及其刻画

在本小节将给出边赋权图对策组内Myerson值的定义及其刻画。

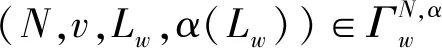
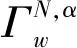
定义2对任意的对策(N,v)∈GN，如果对于任意S⊆N{i},v(S∪{i})=v(S)成立，则参与者i在(N,v)中是一个无效参与者。如果对于任意S⊆N{i},v(S)=0，则参与者i在(N,v)中是一个关键参与者。

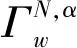
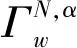
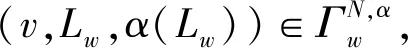
2.2 边赋权图对策组间Myerson值及其刻画

本小节给出边赋权图对策组间Myerson值的定义及其刻画。

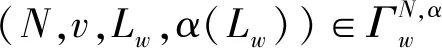
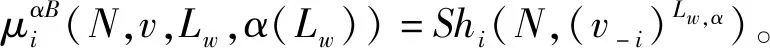
由定义，容易验证μαW+μαB=μα。

下面给出边赋权图对策组间Myerson值的刻画。

3 边赋权图对策组内和组间Myerson值的稳定性

在边赋权图对策中，当在网络中增加边或者增大变得权值时，网络中的参与者是否都是收益的？或者至少这些边关联的参与者是否收益？这就是边或者权的单调性问题或者说稳定性问题。对任意的边赋权图对策，在增加新边或者增大边的权值后，一般来说并不一定所有的参与者，甚至关联的参与者收益。不过，对非负的边赋权图对策，也就是所有联盟的红利非负[14]，组内和组间具有权稳定性和广义稳定性。非负图对策在实际中具有广泛的应用，如河流对策[15]、污染河流对策[16]和排队对策[17]，这些对策都是非负的。

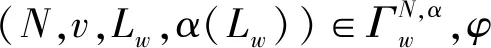
下列命题给出了μαW(v,Lw,α(Lw))的一个表达式。

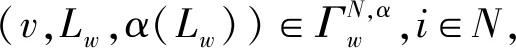
(5)

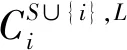
定理3非负边赋权图对策组内Myerson值满足权稳定性。

为了分析边赋权图对策组间Myerson值的权稳定性，首先，我们有下列基本结论。

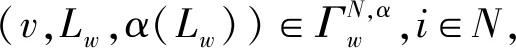
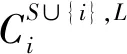
定理4非负边赋权图对策组间Myerson值满足局部权稳定性。

我们用一个例子来说明μαW和μαB满足权稳定性和局部权稳定性。

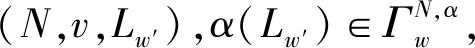
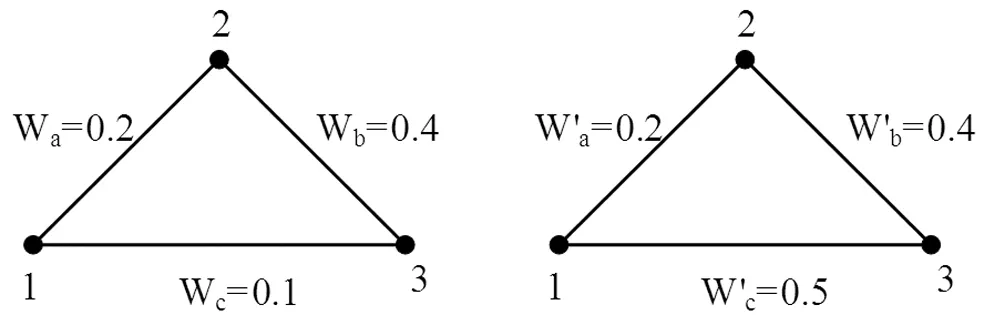
图1 图Lw和Lw′

μα(v,Lw,α(Lw))=(0.183,0.333,0.283)

μαW(v,Lw,α(Lw))=(0.183,0.300,0.283)

μαW(v,Lw,α(Lw))=(0,0.033,0)

和μα(v,Lw′,α(Lw′))=(0.417,0.367,0.517)

μαW(v,Lw′,α(Lw′))=(0.417,0.367,0.450)

μαB(v,Lw′,α(Lw′))=(0,0,0.067)

通过计算结果可以看出，增加边c的权重，则每个参与者的组内Myerson值μαW组间Myerson值μαB都有所增加，并且与c关联的参与者1和3的组间Myerson值μαB都至少不减。但是参与者2的组间Myerson值μαB减少了。因此μαW是稳定的，而μαB是局部稳定的。

接下来我们继续在红利非负的前提下，讨论μαW和μαB的广义稳定性。

定理5对于非负边赋权图对策，若新增边的权重不小于包含这条边的所有圈上边权的最小值，则μαW满足广义稳定性。

在红利非负的情况下，新增的边l*的权重不小于包含l^*的所有圈上边权的最小值的时候，μαW是满足广义稳定性。但是对于μαB，如例中所示，μαB是不满足广义稳定性的。

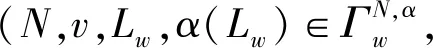
图2 图Lw和图(L∪{l*})w′

显然，该边赋权图对策为非负的。通过边赋权图对策Myerson值、边赋权图对策组内Myerson值和边赋权图对策组间Myerson值的定义，计算可得

μα(N,v,Lw,α(Lw))=(0.167,0.367,0.267)

μαW(N,v,Lw,α(Lw))=(0.167,0.300,0.267)

μαB(N,v,Lw,α(Lw))=(0,0.067,0)和

μα(v,(L∪{l*})w′,α((L∪{l*})w′))=(0.417,0.367,0.517)

μαW(v,(L∪{l*})w′,α((L∪{l*})w′))=(0.417,0.367,0.450)

μαB(v,(L∪{l*})w′,α((L∪{l*})w′))=(0,0,0.067)

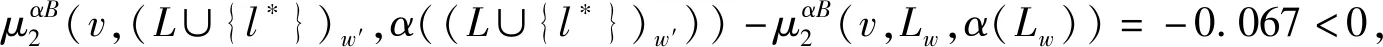
但是对于红利不均是非负的情况，如特征函数v=u{1,3}-3u{1,2}-u{2,3}，通过边赋权图对策Myerson值、边赋权图对策组内Myerson值和边赋权图对策组间Myerson值的定义，计算可得

μα(N,v,Lw,α(Lw))=(-0.233,-0.433,-0.133)

μαW(N,v,Lw,α(Lw))=(-0.233,-0.500,-0.133)

μαB(N,v,Lw,α(Lw))=(0,0.067,0)和

μα(v,(L∪{l*})w′,α((L∪{l*})w′))

=(-0.250,-0.700,-0.250)

μαW(v,(L∪{l*})w′,α((L∪{l*})w′))

=(-0.250,-0.700,-0.050)

μαB(v,(L∪{l*})w′,α((L∪{l*})w′))

=(0,0,-0.200)

注意到此时组内Myerson值μαW和组间Myerson值μαB都不满足广义稳定性。

4 结论

为了区别参与者在所参与联盟的获利和作为其他参与者中介获利的情况，本文在边赋权图对策中定义了组内Myerson值和组间Myerson值，组内Myerson值用于衡量该参与者对所参加联盟的贡献程度；而组间Myerson值评估了该参与者作为其他参与者中介所获得的收益。同时，证明了这两个值能够用可加性、无效参与者性和关键参与者性进行唯一性刻画。在边权重表示边的通讯容量前提下，证明了非负边赋权图对策组内Myerson值和组间Myerson值分别满足权稳定性和局部权稳定性。另外，证明了非负组内Myerson值满足广义稳定性，举例说明了组间Myerson值不满足广义稳定性。由于边权可以表示多种实际含义，有时，在不同含义下边赋权图Myerson值的性质有很大差别，那么在其他边权意义下，组内Myerson值和组间Myerson值具有稳定性的条件是需要进一步深入讨论的问题。此外，我们还可以基于对策理论的视角，将边赋权图对策的组内Myerson值和组间Myerson值这两个值作为中心性度量，衡量参与者在边赋权图代表的社会网络中发挥的作用或产生的经济效益，对合作收益的分配具有指导性的意义。