恐怖分子入侵阻止网络的双层规划建模与禁忌搜索分析
2020-11-10项寅
项 寅
(苏州科技大学 商学院,江苏 苏州 215009)
0 引言
自上世纪90 年代以来,境外“东突”恐怖势力与境内极端宗教组织相互勾结,以分裂中国及建立“东突厥斯坦伊斯兰国”为目的,在新疆各地频频制造暴恐事件,严重影响边疆发展和稳定。随着“一带一路”战略的提出和实施,我国和沿线国家的合作交流不断加深,境内外人员往来日益密切,大大增加了恐怖分子潜入的可能性。因此,如何设计有效的恐怖分子入侵阻止网络,如何通过有限安检资源在边境交通网络中的合理分配来提前识别和拦截正在潜入的恐怖分子并降低袭击风险,已经成为当前意义重大且急需破解的难题。
“9·11”事件后,恐怖主义问题逐渐引起学术界关注,伴随着近十几年全球恐怖活动的愈演愈烈,相关问题的研究也更加完善深入。在管理科学领域,其研究视角大体为三类。第一类视角聚焦于恐怖主义的内在特征规律分析,利用复杂网络、数据分析等实证方法研究恐怖组织的结构特征[1,2]、恐怖袭击偏好及特点[3,4]、恐怖袭击预测及风险评价[5,6]等问题。第二类视角聚焦于反恐应急问题,结合运筹优化方法研究袭击后的应急疏散[7,8]、袭击前的关键设施防护[9,10],以及应急设施选址[11,12]等问题。第三类视角则立足于政府、恐怖分子间的非合作博弈问题,基于博弈理论研究安检资源量[13~15]、防御密度和防御范围[16]、政府和恐怖分子的认知差异[17]、情绪类型[18]、心智特征[19]等对反恐博弈的影响机制。现有研究为政府反恐维稳提供了广泛的决策咨询,但仍忽略了一些重要问题。例如如何从预防性角度出发,通过设计恐怖分子入侵阻止网络来降低袭击风险的研究,还很少涉及。
恐怖分子入侵阻止网络设计方面,网络阻断模型提供了理论借鉴。在传统的网络最大流、最短路、最大可靠路问题上,网络阻断又添加一类新的决策主体,并将传统图论问题拓展为阻断者、入侵者间的主从对策问题。其中,阻断者为先行者,对网络中的部分边进行阻断,以减少对应路段的流量、通行概率或增加其距离,进而减少入侵者效用;入侵者为跟随者,在剩余网络中通过最优决策,来最大化源点汇点间流量、通行概率,或最小化源点汇点间的最短距离。因此,基于入侵者的效用差别,网络阻断问题由最大流阻断[20]、最短路阻断[21]和最大可靠路阻断[22]三类问题构成。
类似于最大可靠路阻断问题,边境反恐中存在类似的两类决策者,即政府和恐怖分子。政府通过阻断交通网络中的部分路段,来降低恐怖分子在这些路段上的通行能力,并最终减少其从境外潜入至境内的概率。然而,传统网络阻断问题存在一个很强的假设条件,即入侵者源点、汇点需为固定,并大大限制了其在反恐安检问题中的应用。现实中,恐怖分子不但可通过袭击效用的比较来选择最优的入侵点,还可对袭击策略做出选择,包括“纯策略”和“混合策略”。
因此,本文旨在突破上述瓶颈,将传统网络阻断理论应用到反恐领域。在此结合反恐情境改进传统模型并提出一类新的恐怖分子入侵阻止网络模型,进而为政府边境安检资源分配和安检能力改善提供参考方案。与传统最大可靠路阻断模型不同,本文模型首先将袭击风险定义为政府和恐怖分子的效用函数;其次松弛源汇点必须固定的假设前提并将入侵点作为恐怖分子的决策变量;最后将恐怖分子的计算能力反映在模型之中,分析恐怖分子“纯策略”和“混合策略”下的入侵方式,及其对政府防御策略的影响。
1 数学模型
1.1 问题描述
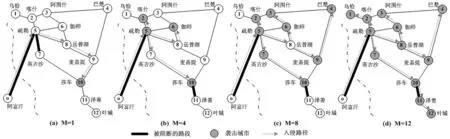
恐怖分子入侵阻止网络设计问题包含政府和恐怖分子两类参与人,政府的决策目标是最小化袭击风险,恐怖分子的目标则正好相反。其中,政府是阻止网络的设计者,恐怖分子则在给定的阻止网络中决策最优的袭击节点和入侵路径。决策过程如图1所示:
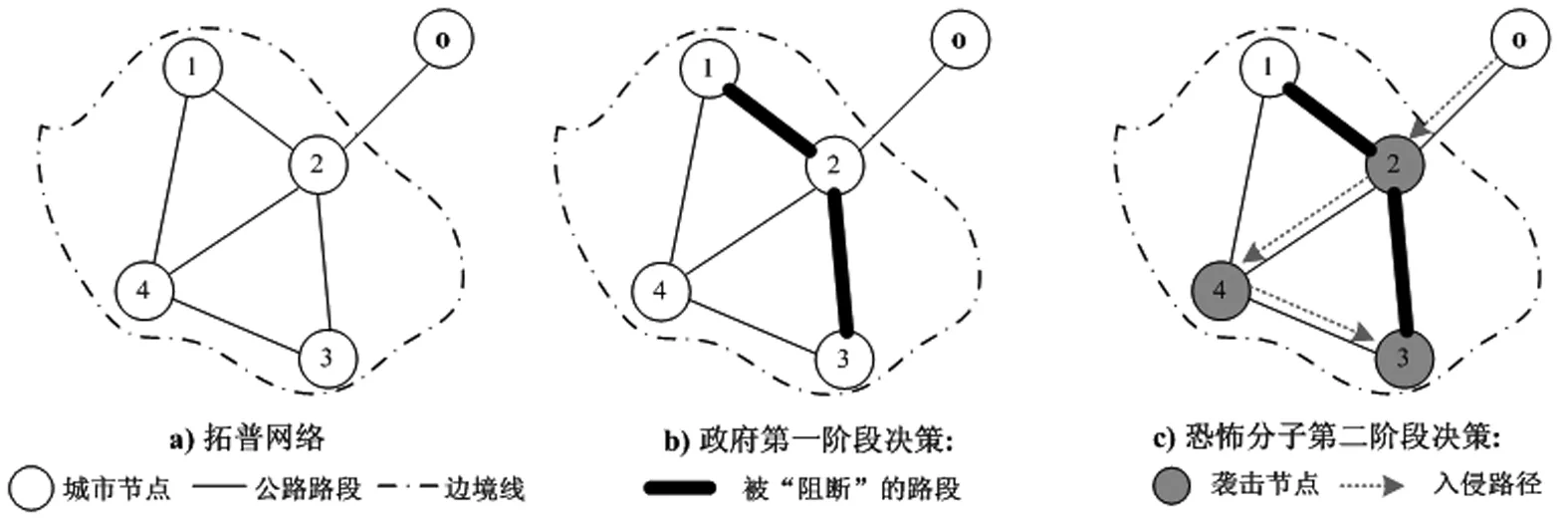
图1 问题描述图
首先,图1a表示某国交通拓扑网络图。其中的点画线代表该国边境线,境外的节点o代表恐怖分子的入侵源点,境内的所有节点{1,2,3,4}代表该国家的城市,且均存在受袭击的风险。每个城市节点包含两个权重,分别表示对应城市发生袭击前提下产生袭击后果的条件概率,以及相应的袭击后果。网络中的边则代表两城市间的公路路段,每条路段同样包含两个权重,分别表示对应路段在未被阻断或已被阻断前提下,恐怖分子成功通过该路段而未被抓住的概率。其次,决策过程包含两个阶段,具体如下:
第一阶段为袭击发生前,在有限的资源下,政府首先选择网络中的部分路段进行阻断,并完成阻止网络设计。阻断理解为在对应路段建立安全检查站点,并对往来人员车辆进行严密的安全检查,作用是降低恐怖分子在这些路段的通过概率。例如在图1b中,政府对路段(1,2)和(2,3)实施阻断,并降低了恐怖分子关于该路段的通过概率。
第二阶段反映袭击过程。恐怖分子通过新闻、互联网、实地考察而掌握政府阻断布局后,首先决策袭击点,随后优化固定源点到袭击点的入侵路径。在此充分考虑恐怖分子的计算能力,并通过一类混合策略进行刻画。定义该混合策略包含M类情形,并假设恐怖分子以1/M的等概率去袭击使其效用最大的、次大的…第M大的节点,M取值越小,恐怖分子的计算能力越高。例如:①M=1表示恐怖分子有极高的计算能力,其可以精确计算出效用最大的袭击点并以1的概率袭击,此时混合策略转为纯策略;②M=n表示恐怖分子计算能力极弱的情形,其无法比较任意两节点间的差异,此时各节点的袭击效用对其而言是相同的,因此以1/n的等概率袭击每一个节点,这里的n代表城市节点总数。③M{1,2, 3,…,n-1}时,受计算能力限制,恐怖分子只能大概地计算出效用较大的前M个节点而无法进一步区分优劣,因此以1/M的等概率袭击这些节点。显然,当M越小,恐怖分子就越能缩小袭击效用较大节点的所在范围,其计算能力就越高。以图1c为例,恐怖的计算能力用M=3表示,在观察到政府阻断方案后,其分别以1/3的概率袭击节点2,3,4,对应入侵路径依次为o-2,o-2-4-3,o-2-4。
综上所述,该问题可描述为:针对恐怖分子的混合袭击策略,政府应如何决策有限阻断资源在交通网络中的最优分配,才能最小化恐怖分子的袭击效用?
1.2 模型假设
具体的模型假设包括:
假设1网络的拓扑结构和参数均是确定的,不考虑随机、时变、动态等情形。
假设2政府和恐怖分子关于网络拓扑结构、网络参数的掌握是完全的、对称的。
假设3恐怖分子可通过报纸、新闻、实地考察来掌握政府阻断的布局信息。
假设4恐怖分子的计算能力用M{1,2,3,…,n}表示,M越大计算能力越低。对应不同的计算能力,恐怖分子分别以1/M的等概率去袭击效用最大的、次大的…第M大的节点,且各节点的袭击相互独立。为保证建模可行,这里的混合策略仅涉及袭击节点的选择,而关于源点和给定袭击点间的入侵路径则仍以纯策略形式决策。
假设5每条路段最多只能被阻断一次。
假设6政府和恐怖分子的效用与袭击风险有关。在此参考兰德公司的定义[5],袭击风险=袭击发生概率(威胁)×袭击发生前提下产生后果的条件概率(脆弱性)×产生后果前提下的袭击后果(后果)。其中,袭击发生概率等于恐怖分子穿越阻止网络并成功到达袭击点的概率;后两项主要和城市安保能力及人口数量相关,具体大小通过节点权重来反映。
1.3 符号定义
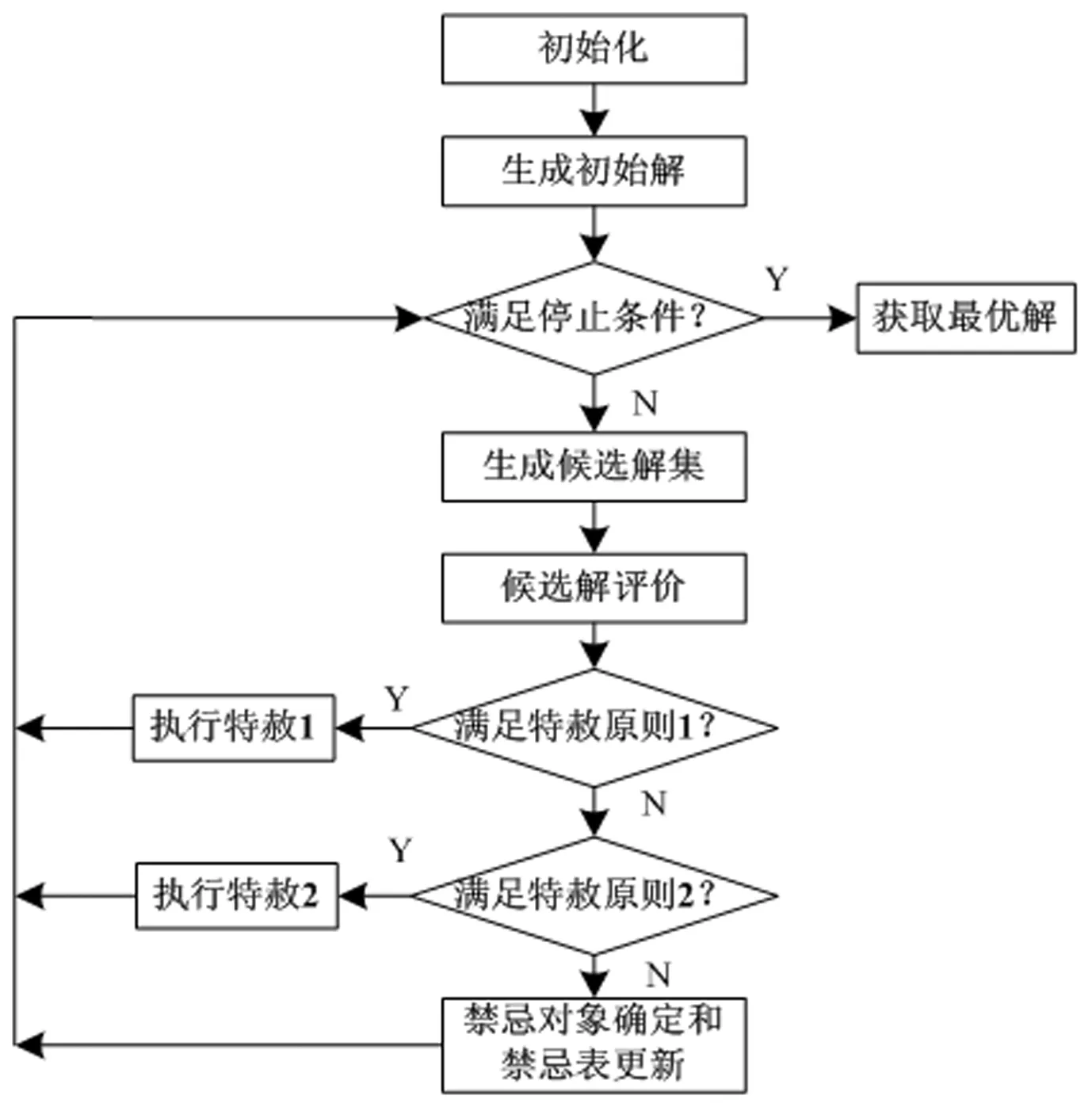
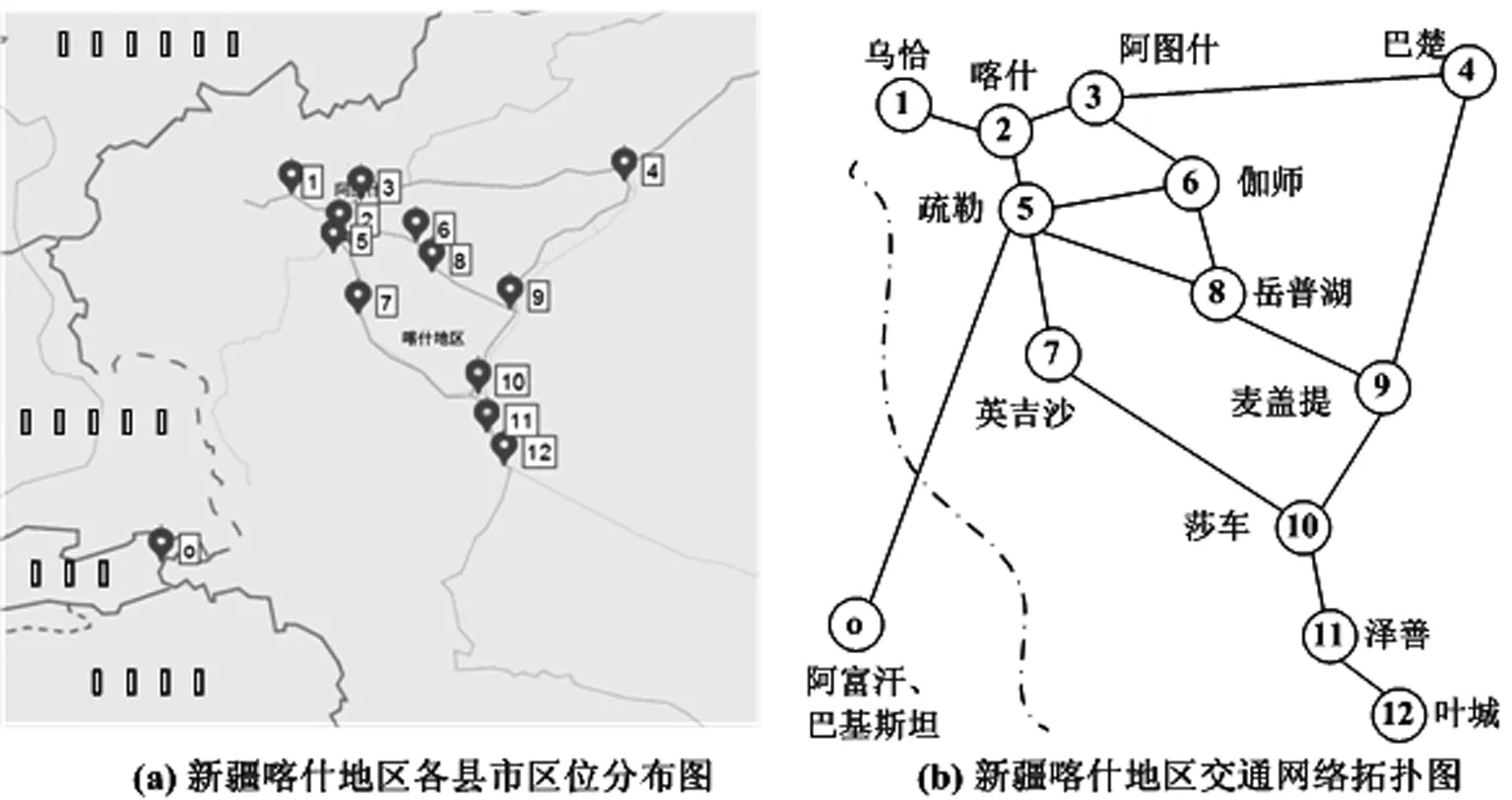
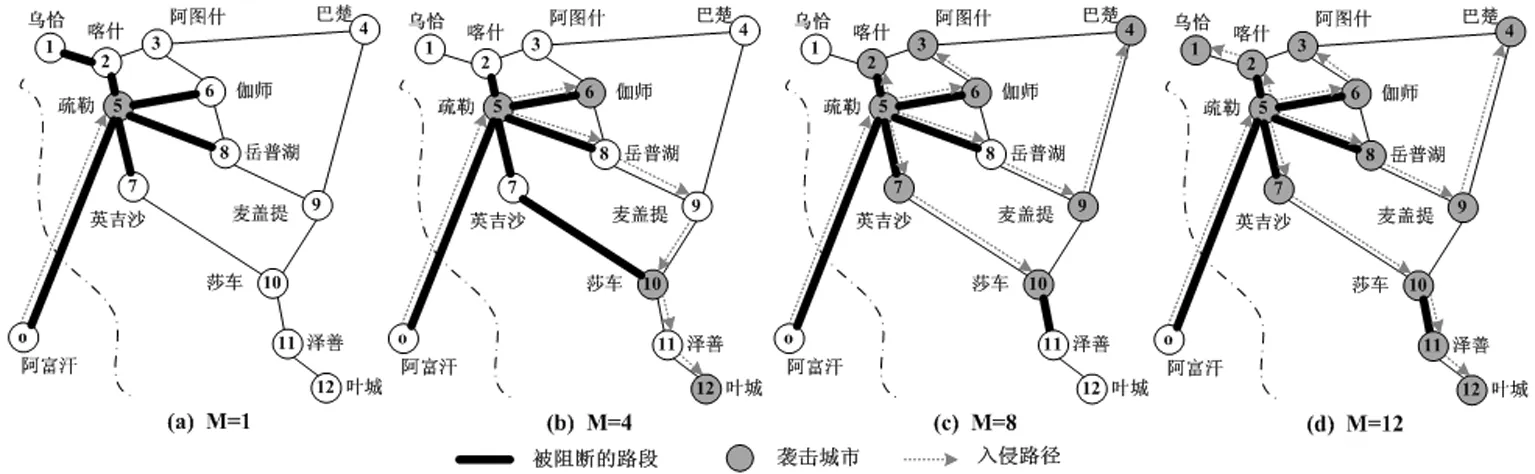
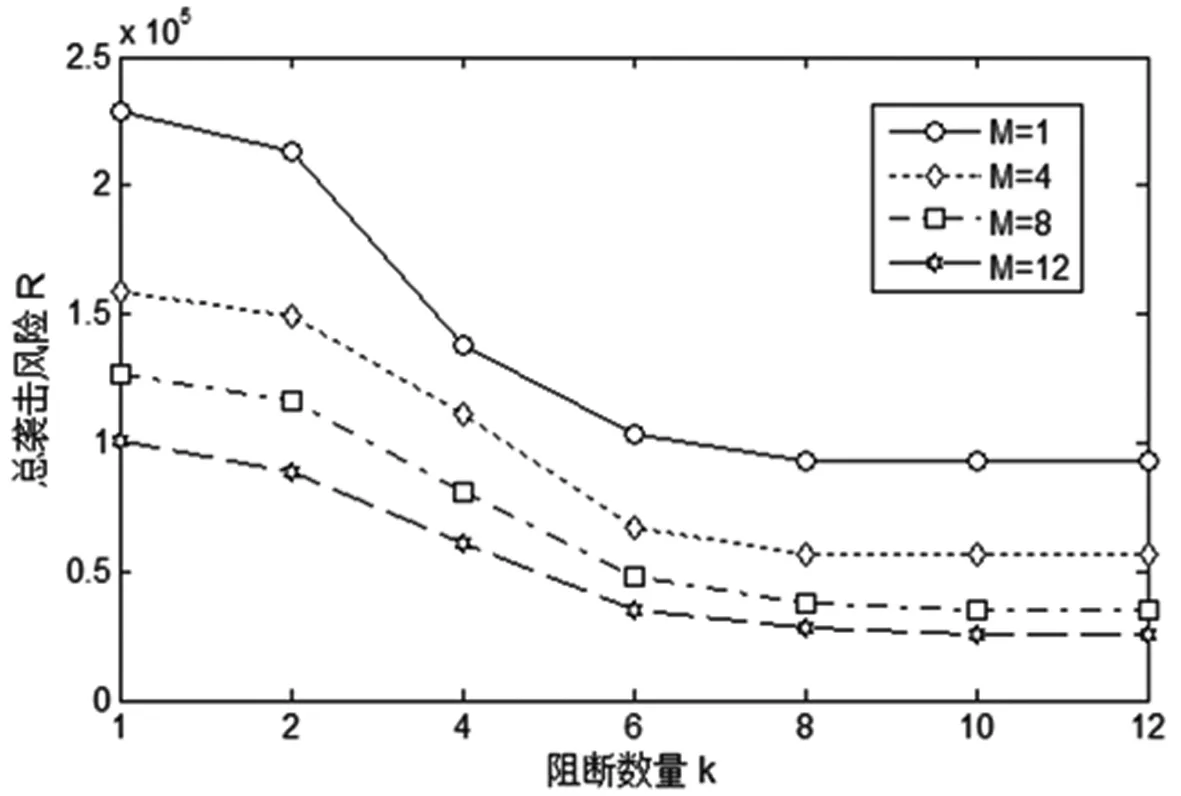
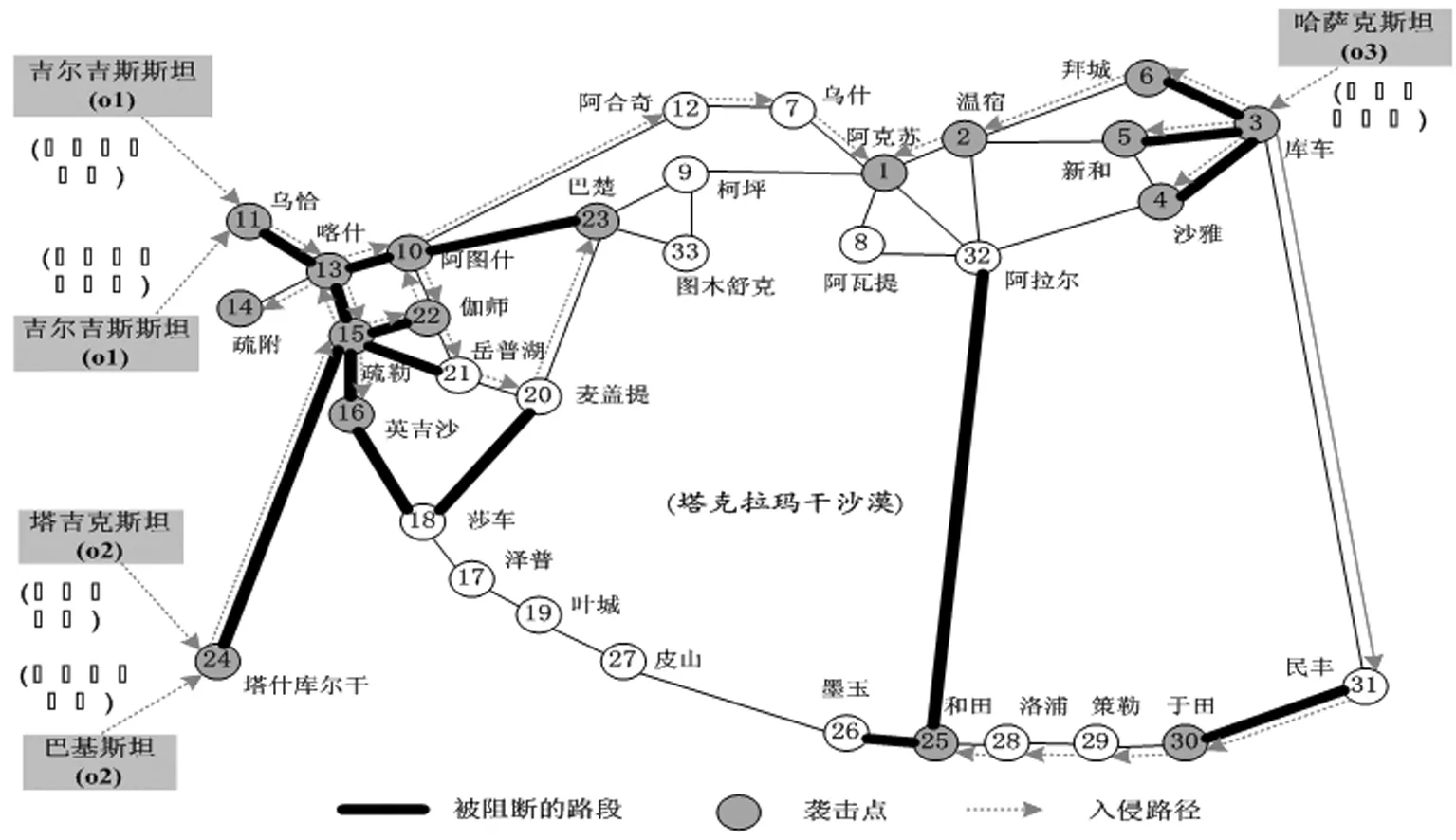
首先定义集合与参数。设N′={i:i∈N′}为网络节点集,其中的o为恐怖分子入侵源点,N=N′/{o}为城市节点集,总数记为n。设A={(i,j):(i,j)∈A}为公路路段集。设FS(i)和RS(i)分别为所有从节点i发出的弧的集合和所有汇聚到节点i的弧的集合。设k为政府的阻断数量;设任意节点i的权重πi和wi分别为该节点发生袭击前提下产生后果的条件概率及相应的袭击后果。设任意路段(i,j)的权重pij和qij分别表示该路段在未被阻断和已被阻断时,恐怖分子成功通过而未被抓获的概率,且满足0 (1) (2) (3) 根据问题描述中政府和恐怖分子的主从对策关系,恐怖分子入侵阻止网络设计问题被构建为如下双层规划: (4) (6) 其中,z,y是下层规划的解 (12) 上述模型中,式(4)~(6)为政府阻止网络设计的上层规划;式(7)~(12)则为恐怖分子在给定阻止网络下决策袭击节点和入侵路径的下层规划。其中,上层决策变量x以参数形式出现在下层规划,而下层决策变量z,y同样以参数形式出现于上层规划。 目标函数(4)表示政府最小化袭击风险;约束(5)表示在有限资源下,政府仅能阻断k条路段;约束(6)限定上层变量x为0-1变量;目标函数(7)表示恐怖分子最大化袭击风险;约束(8)保证恐怖分子在每类袭击情形中只袭击一个节点;约束(9)保证混合策略各类情形中的袭击点各不相同;约束(10)为恐怖分子源点和袭击点间的流量平衡约束,并保证其选择的路段集合可构成一条首尾连接的路径;约束(11)~(12)限定下层变量z,y为0-1变量。 上述模型为非线性双层规划,且目标函数中的非线性乘积项增加了求解难度。因此,为便于模型求解,本节对上述模型提出相关引理,并给予证明。而这些引理则将被用于下一节的算法设计。 引理1针对固定袭击情形m,给定上层变量x的值,并固定袭击变量zm后,下层规划可转为仅关于变量ym的最短路径问题,且最优解下的路段选择方案ym与袭击变量zm唯一对应。 引理2通过下层规划的决策,恐怖分子最优混合策略下所有袭击情形中的袭击节点,必定是使其效用最大的、次大的…第K大的袭击节点。 双层规划属于NP-难题。鉴于精确解算法很难在多项式时间内进行求解,又由于本模型目标函数存在复杂的非线性项,固选用搜索能力强、收敛速度快的禁忌搜索算法。考虑到上下层的决策变量较多,因此仅通过禁忌搜索算法来实现上层变量x的迭代和更新。给定上层变量的值后,下层规划z,y的求解则根据引理1~引理2,通过设计一类多项式时间可解的精确解算法来实现。 由于下层目标函数中存在难以处理的非线性部分,因此很难对下层变量z,y同时求解,而须使用分而治之的方法。因此,结合引理1,在给定上层变量x的前提下,首先通过袭击点变量zm的穷举来将下层规划分解并转化为n个仅关于单一变量ym的最短路径问题。随后,分别求解各组最短路问题,并将各组解依次代入式(3)来计算不同袭击点下恐怖分子的效用值。最后,结合引理2,选择最大效用、次大效用…第M大效用所对应的解作为下层规划的最优解,并对每组解赋予1/M的发生概率。具体的步骤如下: 算法1 步骤2袭击节点穷举。若t>n,转步骤5;否则,令袭击点为t,即zt=1,zt=0,∀i≠t的情况,并将此时的袭击变量简记为向量zt。 步骤4可行解评价。将给定的上层变量和下层规划当前可行解(zt,yt)一起代入式(3),并计算恐怖分子效用值Rt,令t=t+1,并返回步骤2。 步骤5最优解确定。对n组可行解的效用值Rt,t∈{1,2,…,n}降序排列,排序后记为{R(1),R(2),…,R(M),…,R(n)}。取前M大效用值{R(1),R(2),…,R(M)}对应的可行解作为下层最优解,记为{(z,y)(1),(z,y)(2),…,(z,y)(M)},分别赋予各可行解1/M的发生概率,并定义为M种不同袭击情形。 显然,算法1通过袭击点穷举,将下层规划分解并转化为n个简单的最短路径问题。由于dijkstra算法求解两点间最短路径的计算时间复杂性为O(n)2,所以n次最短路径问题求解的计算时间复杂性就为O(n)3。因此,给定上层变量的值后,下层规划可在多项式时间内求解。 个体适应度计算:具体计算分3步。首先,解码染色体,将阻断变量x代入下层规划(7)~(12),利用算法1求得下层规划解(z,y)。其次,将当前解(x,z,y)代入式(3)并计算袭击风险R。最后,结合政府最小化袭击风险的目标,将1/R作为该染色体的适应度值。 初始解生成:随机生成2n条染色体,依次计算适应度,选择适应度最高的染色体作为初始个体。 邻域搜索和候选集:利用互换(swap)策略进行邻域搜索。将染色体X中某初始值为1的元素置为0,同时将某初始值为0的元素置为1,即完成一次互换。当X中元素1的个数为k时,就将互换产生的所有k×(n-k)个新个体作为当前的候选集。例如X={0,1,0,1}的候选集为{1,0,0,1},{0,0,1,1},{0,1,1,0},{1,1,0,0}。 禁忌表设计:禁忌表由禁忌对象和禁忌长度两部分组成,主要通过限制任期内的禁忌对象成为下一次迭代的初始解,来避免迂回搜索并提高搜索效率。为减少存储空间,选择候选解中非禁忌的最优个体的适应度值作为禁忌对象,禁忌长度则在[1,n]中随机取整。 特赦原则:特赦原则采用评价值准则和最小错误准则相结合的方法。前者要求当被禁忌的候选解适应度高于当前全局最优解的适应度时,解禁该候选解并更新最优解;后者则要求当所有候选解均被禁忌时,选择适应度最高的候选解进行解禁。 停止条件:若当前迭代次数大于最大迭代数,则算法停止。 禁忌搜索算法: 步骤0初始化。输入模型参数,设置最大迭代次数Imax。初始化当前迭代次数h=1,全局最优解的适应度值Fopt=0,全局最优解Sopt=Ø,禁忌表List=Ø。 步骤1生成初始解。随机生成2n条染色体,将适应度最高的染色体作为初始解ISh。 步骤2停止条件判定。若h≤Imax,转步骤3,否则,转步骤8。 步骤3生成候选集。利用互换策略实现ISh的邻域搜索,将得到的TN=k×(n-k)个新个体作为当前候选集S。 步骤4候选集评价。针对S={S1,S2,…,STN}中的每个个体Si(i=1,2,…,TN),依次计算每个个体的适应度值Fi。 步骤5特赦原则判定。若满足评价值准则,即Fi*>Fopt(i*∈argmaxiFi),转步骤6a;若满足最小错误准则,即{S1,S2,…,STN}⊆LIst,转步骤6b;否则,转步骤7。 步骤6a特赦执行。更新Fopt=Fi*,Sopt=Si*(i*∈argmaxiFi)。令h=h+1,令下次迭代初始解为ISh=Si*,List中所有禁忌对象的禁忌长度减1,返回步骤2。 步骤6b特赦执行。令h=h+1,ISh=Si*(i*∈argmaxiFi),List中所有禁忌对象的禁忌长度减1,返回步骤2。 图2 禁忌搜索算法流程图 步骤7禁忌对象确定及禁忌表更新。List中各禁忌对象的禁忌长度减1,并在所有非禁忌的候选解{Sj|Sj∈SList}中选择适应度最高的个体Sj*(j*∈argmaxjFj)作为新的禁忌对象,令List=List∪Sj*,禁忌长度在[1,n]中随机取整。令h=h+1,ISh=Sj*,返回步骤2。 步骤8获取最优解。解码Sopt后可得到最优阻断策略x*,将其代入下层规划,并通过算法1得到最优的袭击节点和路段选择策略(z*,y*)。 禁忌搜索的算法流程图如下所示: 以我国边境地区喀什为例进行算例分析。该地区主要县市的区位分布如图3a所示。将县市抽象为节点、路段抽象为边后得到的交通拓扑网络图如图3b所示,共由13个节点和16条边组成。 图3 喀什地区县市分布图和交通网络拓扑图 其中,源点o为境外恐怖分子的入侵源点,节点1-节点12则为境内县市节点。假设袭击总能成功,即将各节点i的权重πi统一为1,而权重wi则近似为对应城市的人口总数。相关数据如表1所示,数据来源为《2017年新疆统计年鉴》。各路段(i,j)在未阻断时恐怖分子的通行概率pij根据专家评估而定,具体数值如表2所示,而各路段(i,j)被阻断后恐怖分子的通行概率qij则统一为0.3,即考虑阻断能力满足标准化的情形。 表1 各节点i的权重值wi 表2 恐怖分子成功通过未被阻断的路段(i,j)而未被抓获的概率pij 针对上述算例,根据阻断数量k={2,4,6}的不同取值来设计3类情境,又在每类情境中分别考恐怖分子计算能力为M={1,4,8,12},即{极强、较强、较弱、极弱}的情形。在装有Inter Core i7 2.6GHz处理器、4GB RAM的联想笔记本电脑上,利用Matlab 2014编译穷举算法和禁忌搜索算法,并比较两类算法的计算时间和计算精度。具体计算结果如表3所示: 表3 各情境下的计算结果比较 在表3中,tEX和REX分别表示穷举算法的计算时间和最优解下的袭击风险值。tTA和RTA分别表示用禁忌搜索算法连续计算3次的平均时间和平均袭击风险值。e=(RTA-REX)/REX表示禁忌搜索算法的误差率。由表3可知:在计算时间方面,穷举算法的计算时间随阻断数量k的增加而急剧上升,但禁忌搜索的计算时间则比较稳定且不受k的影响;在计算精度方面,误差率随着决策规模k的变大而增加,但总体误差小于2%。说明禁忌搜索算法具有较少的计算时间成本和较高的计算精度。 利用穷举算法计算表3中各决策情形的精确解,并对最优的决策方案进行分析。 首先,情境1表示政府阻断数k=2的情况。其中: 当M=1时,恐怖分子计算能力极强,最优决策见图4a。政府一方面阻断入境的必经路段(o,5),另一方面阻断路段(5,7)以监控到达权重最大节点莎车的最近路径o-5-7-10。恐怖分子选择最大权重节点莎车袭击,入侵路径为o-5-8-9-10。 当M=4时,恐怖分子计算能力较强,最优决策见图4b。与图4a相比,政府将原位于路段(5,7)的阻断移至路段(10,11),以监控通向叶城和泽善的必经路段,并降低了大权重城市叶城的袭击发生概率。恐怖分子则分别以1/4的等概率袭击大权重的喀什、伽师和莎车,以及离其源点最近的疏勒。入侵路径依次为o-5-2,o-5-8-6,o-5-7-10和o-5。 当M=8时,恐怖分子计算能力较弱,最优决策见图4c。政府阻断方案与图4b相同,而除小权重的乌恰、岳普湖、泽善,以及被封锁住必经路段的大权重城市叶城外,恐怖分子分别以1/8的等概率袭击其他节点。入侵路径为:o-5,o-5-2,o-5-8-6,o-5-7,o-5-8-6-3,o-5-8-9,o-5-8-9-4和o-5-7-10。 当M=12时,恐怖分子计算能力极弱,最优决策见图4d。与图4c相比,政府阻断方案不变,恐怖分子则以等概率袭击每一个城市。入侵路径分别为:o-5,o-5-2,o-5-2-1,o-5-8,o-5-8-6,o-5-7,o-5-8-6-3,o-5-8-9,o-5-8-9-4,o-5-7-10,o-5-7-10-11,o-5-7-10-11-12。 图4 关于情境1的最优决策分析图 其次,情境2表示政府阻断数k=4的情况。其中: 当M=1时,恐怖分子计算能力极强,最优决策见图5a。政府除阻断必经路段(o,5)外,一方面阻断路段(5,7)(9,10)以监控通向英吉沙、莎车、泽善和叶城的必经路段并降低这些城市的袭击率,另一方面阻断(5,8)以迫使恐怖分子不能选择通行概率最大的路径o-5-8-6来到达大权重的伽师,而只能选择通行概率较小的路段o-5-6。恐怖分子不再袭击权重最大的莎车,而是选择路径o-5-6去袭击伽师。 当M=4时,恐怖分子计算能力较强,最优决策见图5b。政府除阻断必经路段(o,5)外,还对路段(3,4)(5,7)(8,9)进行阻断,监控了通向英吉沙、巴楚、麦盖提、莎车、泽善、叶城的必经路段,并降低了这些城市的袭击发生率。恐怖分子分别以1/4的概率袭击大权重的喀什、伽师和莎车,以及离其源点最近的疏勒。入侵路径依次为:o-5-2,o-5-8-6,o-5-7-10和o-5。 当M=8时,恐怖分子计算能力较弱,最优决策见图5c。政府的阻断方案不变,恐怖分子则分别以1/8的概率袭击除小权重城市乌恰、英吉沙、麦盖提、泽善外的全部节点。与图5b相比,新增袭击点阿图什、巴楚、岳普湖、叶城的入侵路径依次为:o-5-8-6-3,o-5-8-9-4,o-5-8,o-5-7-10-11-12。 当M=12时,恐怖分子计算能力极弱,最优决策见图5d。政府的阻断方案不变,恐怖分子则以等概率袭击全部节点。与图5c相比,新增袭击点乌恰、英吉沙、麦盖提、泽善的入侵路径依次为:o-5-2-1,o-5-7,o-5-8,o-5-7-10-11。 图5 关于情境2的最优决策分析图 其次,情境3表示政府阻断数k=6的情况。其中: 当M=1时,恐怖分子计算能力极强,最优决策见图6a。政府对路段(o,5)(5,2)(5,6)(5,8) (5,7)(2,1)进行阻断,封锁住了到达疏勒以及由疏勒向外发散的所有路段。恐怖分子被迫袭击离源点最近的疏勒,入侵路径为o-5。 当M=4时,恐怖分子计算能力较强,最优决策见图6b。在图6a的基础上,政府将路段(1,2)的阻断移至路段(7,10),以进一步监控通向大权重城市莎车的近端路径o-5-7-10。恐怖分子分别以1/4的概率袭击疏勒、伽师、莎车和叶城,入侵路径依次为o-5,o-6,o-8-9-10,o-8-9-10-11-12,由于这些路径包含了多条被阻断的路段,因此恐怖分子的到达概率被降低。 当M=8时,恐怖分子计算能力较弱,最优决策见图6c。在图6c的基础上,政府将路段(7,10)的阻断移至路段(10,11),以进一步强化关于大权重城市叶城的防御。恐怖分子以1/8的概率袭击除乌恰、岳普湖、泽善和叶城外的所有节点。与图6b相比,新增袭击点喀什、阿图什、英吉沙、麦盖提、巴楚的入侵路径依次为:o-5-2,o-5-6-3,o-5-7,o-5-8-9,o-5-8-9-4。 当M=12时,恐怖分子计算能力极弱,最优决策见图6d。政府的阻断方案不变,恐怖分子则以等概率袭击全部节点。与图6c相比,新增袭击点乌恰、岳普湖、泽善和叶城的入侵路径依次为:o-5-2-1,o-5-8,o-5-7-10-11,o-5-7-10-11-12。 图6 关于情境3的最优决策分析图 结论1无论恐怖分子计算能力如何,大权重城市和离开源点较近的城市均为受袭频率较高的城市。政府的最优阻断方案会受恐怖分子计算能力影响,但仍存在共性,并总是针对离开源点较近或者通向某些城市群的唯一必经路段进行优先阻断。 管理启示1政府一方面应提升重要城市和边境口岸城市的安保能力和应急管理能力,以用来降低袭击成功率和袭击后果;另一方面需合理规划安检站点在公路网络中的布局,识别通向某些城市群的关键路段,并完成关键路段的全面安检监控。 分别考虑恐怖分子计算能力为M{1,4,8,12}的情况,利用穷举算法依次计算阻断数量k{1,2,4,6,8,10}时最优解下的袭击风险,绘制相关曲线图,并主要分析计算能力和阻断数量对于袭击风险的影响。具体关系图见图7。 图7 阻断数量及理性程度对袭击风险的影响分析图 在图7中,横坐标表示阻断数量k,纵坐标表示袭击风险R,图例中的“圆形”、“菱形”、“方形”和“五角星”则分别对应了恐怖分子计算能力为M∈{1,4,8,12}的情形。根据图7可发现:首先,固定计算能力M后,袭击风险R随阻断数k的增加而下降,但下降程度逐渐减少;其次,固定阻断数k后,M取值越大,即计算能力越低时,袭击风险R也越低。 结论2恐怖袭击风险和政府安检资源投入水平相关,安检资源投入越多,袭击风险越小,但当安检资源多达一定程度后,继续增加不能再发挥作用,且袭击风险保持不变。 管理启示2政府不能盲目通过增加安检资源投入来降低袭击风险,而应权衡袭击风险、物流效率和财政经费三大要素,将资源的利用效率作为评估标准,避免资源闲置现象和薄弱防御环节出现。结合图7可知,不论恐怖分子的计算能力如何,喀什边境交通网络中的最优阻断数量均应取6。 结论3随着恐怖分子计算能力的降低,网路中城市节点的受袭风险也逐渐降低。 管理启示3首先,政府应重视恐怖袭击相关数据收集,结合定性分析、数据挖掘方法来合理定义、评估、预测恐怖分子的知识水平和计算能力,进而有针对性地开展防御部署。其次,政府可通过反恐信息隐藏来干扰和弱化恐怖分子的计算能力,以降低风险。例如,政府可利用人工智能和传感技术来设计一些“隐蔽”的阻断,误导恐怖分子的最优袭击方案,并降低袭击风险。 结合整个南疆交通网络进行实例分析,考虑“多入侵源点”的情形,利用反恐阻止网络模型识别南疆“关键”路段和“高风险”城市,为反恐部门提供参考。我国南疆地区与哈萨克斯坦、吉尔吉斯斯坦、塔吉克斯坦、阿富汗和巴基斯坦毗邻,包含33个主要的县市,具体区位分布如图8所示。目前,我国已在南疆地区开设的陆路口岸包括吐尔尕特口岸(乌恰县)、伊尔克什坦口岸(乌恰县)、红其拉甫口岸(塔什库尔自治县)、卡拉苏口岸(塔什库尔自治县)和木扎尔特口岸(库车县)。 图8 南疆地区各县市分布图 与5.1节类似,将上述地理分布图抽象为交通网络图,并结合《2017新疆统计年鉴》和专家评议获取城市节点和路段的各类权重。在此将开设陆路口岸的乌恰县、塔什库尔自治县、库车县作为恐怖分子的3个入侵源点,假设从不同源点出发的恐怖分子的袭击相互独立,并将他们的袭击风险和作为阻断方案的评价标准。主要考虑恐怖分子计算能力较强,即M=8的情况,并利用禁忌搜索算法依次计算阻断数为k{4,8,12,16,20,24}时的情形。结果发现,当阻断数k=16时,阻断资源的利用效率最高。具体的决策方案如图9所示。 图9 理性程度M=8,阻断数k=16时的最优决策示意图 由图9可知:最优决策下,政府首先将大部分阻断资源分配于西部边境公路,该地区邻国众多且陆路口岸密集,为境外恐怖分子入侵提供可乘之机,固需重点防御;其次对东部地区由库车发散出的公路进行阻断,以减少恐怖分子由木尔扎特口岸入侵境内的概率;最后,针对中部路段(25,26)和塔克拉玛干沙漠公路(25,32)进行阻断,以拦截恐怖分子由北向南入侵的“捷径”,并降低和田及墨玉的袭击风险。 在给定的阻止网络下,位于西部邻国吉尔吉斯斯坦、塔吉克斯坦和巴基斯坦的境外恐怖分子集中于袭击离口岸较近的乌恰、喀什、阿图什、巴楚等西北部城市,由于恐怖分子均需穿过被阻断路段后才能到达这些城市,因此袭击发生率大大降低。相反,南部地区的莎车、叶城、墨玉、和田等大权重城市则免遭袭击,原因是路段(15,16)(16,18)(15,21)(18,20)(32,25)的阻断封锁了由西北向南入侵的必经路段。此外,位于哈萨克斯坦的境外恐怖分子则偏好袭击北部阿克苏地区的城市群以及南部大权重城市和田及于田。但由于路段(3,6)(3,5)(3,4)(30,31)均被阻断,因此这些城市的袭击发生率也被降低。 管理启示4为防止境外恐怖分子入侵,南疆交通公路安检部署可参考上述“两翼重防,中路拦截”的规划思路。一方面针对西线喀什北部地区和东线环库车地区交通网络重点设防,以实现各边境口岸邻近路段的全面监控;另一方面监控中部“捷径”路段(25,32),以进一步降低南部城市群的袭击风险。同时,还可在喀什北部和阿克苏东部地区的城市群中部署充足的安保和救援资源,以改善高风险城市群的防御和应急能力。 近些年我国西部地区暴恐事件多发,安全隐患不断上升。为防止境外恐怖分子入侵我国, 本文从恐怖袭击事前防御角度出发,提出一类新的恐怖分子入侵阻止网络设计问题,构建模型、设计算法,并结合实例进行仿真分析,以为政府边境反恐提供有效的决策咨询。 考虑到全球反恐战争的漫长性,恐怖主义问题同样具有长远的研究意义。因此,为进一步拟合现实情境并提升应用价值,恐怖分子入侵阻止网络问题的未来研究方向还可包括: 1)考虑信息隐藏策略的阻止网络设计问题。政府可利用人工智能或传感技术来实现一些“隐蔽”的阻断,进而误导恐怖分子的最优决策并降低袭击风险,主要研究政府如何实现“公开”和“隐蔽”阻断的最优布局,并设计巧妙的“陷阱”。 2)阻断资源多类别下的阻止网络设计问题。将安检资源进行类别细分,进一步评估并考虑武警人员、金属扫描仪、太赫兹人体安检仪、传感设施等安检资源间的“协同作用”,进而决策各类有限资源在交通网络中的最优分配。 3)考虑随机或模糊情形的阻止网络设计。现实中政府的阻断能力和恐怖分子的袭击后果存在随机性或模糊性,因此可将静态入侵阻止网络问题拓展到随机情形,构造模型并设计算法。 4)阻止网络的鲁棒性研究。现实中的安检站点可能因停电、罢工等异常事件而导致功能“失效”。未来可针对已有阻止网络进行鲁棒性或敏感性分析,识别关键的阻断路段,并提出预防性措施。
1.4 效用表示
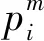


1.5 模型构建

2 相关引理
3 算法设计
3.1 下层规划求解
3.2 双层规划求解
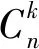
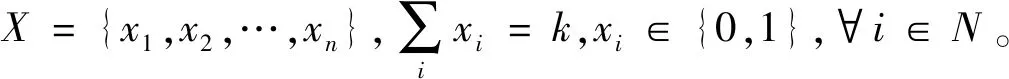
4 算例分析与仿真
4.1 算例描述


4.2 算法性能比较

4.3 最优决策方案

4.4 不同计算能力和阻断数下的风险比较
5 实例应用

6 结论
