木芯复合材料梁柱T形节点顶底角钢连接性能
2020-11-10谢志锦齐玉军刘伟庆
谢志锦,齐玉军,方 海,刘伟庆
(南京工业大学 土木工程学院,江苏 南京 211816)
木芯复合材料构件是以轻木作为芯材,以复合材料作为面层所形成的一种新型夹芯结构。与传统的混凝土及钢结构相比,木芯复合材料构件在相同承载力的情况,质量更轻,外部GFRP(Glassfiber Reinforced Plastic)面层具有良好的耐久性能[1~3]。该种构件可作为梁、柱等构件用于结构工程,特别是在装配式框架结构中具有良好的应用前景。
顶底角钢因变形能力强、延性好等特点常作为节点连接件应用于结构工程之中。已有研究表明,顶底角钢承载力与初始转动刚度较小[4,5]。Garrido等[6]在木芯复合材料楼面板与承重墙的连接中,分别采用胶结和螺栓连接将顶底角钢与构件相连。试验结果表明,相较于胶结连接的脆性破坏,采用螺栓连接的顶底角钢试件表现出更好的塑性变形能力和延性,但其刚度与承载力较低。在实际工程中,常在节点连接处角钢上设置加劲肋,以此增加节点的承载力与刚度。王鹏等[7]在钢结构的梁柱节点连接试验中,在顶底角钢上设置加劲肋,并通过静力加载试验,研究了加劲肋的设置对节点承载力与转动刚度的影响。结果表明,相同情况下,设置加劲肋角钢的节点试件,初始转动刚度及承载力比未设置加劲肋的试件分别提高了95%与148%。郑延银等[8]通过单调加载试验,研究了设置双腹板顶底角钢连接节点的力学性能,并进行了有限元分析。研究结果表明,加劲肋可有效提高节点的初始转动刚度,使节点的塑性开展更缓慢。目前,设置加劲肋的顶底角钢多应用于钢结构设计中,针对木芯复合材料节点连接的研究较少。
基于以上研究成果及工程实际需求,本文针对木芯复合材料梁柱T形节点,设计6种不同顶底角钢构件,通过静力加载试验,研究节点的破坏模式、承载力和初始转动刚度。并针对不同破坏模式,给出承载力计算公式,以期给工程设计及应用提供依据。
1 试验概况
1.1 试件设计
试验中共设计6个木芯复合材料梁-柱角钢连接节点试件,试件编号分别为TJ-110,TJ-160,TJ-210,TJ-110-R,TJ-160-R,TJ-210-R。其中T表示T形节点,J表示Joints,数字表示靠近梁侧角钢肢长,R表示设置加劲肋。所有木芯复合材料构件的截面尺寸均为100 mm×150 mm,梁长800 mm,柱高1600 mm。其中芯材为南方松,截面尺寸为90 mm×140 mm,如图1所示,外包材料为玻纤增强不饱和树脂基复合材料(GFRP),厚度为5 mm,采用真空导入工艺将树脂导入玻璃纤维织物,待树脂固化后,形成木芯复合材料构件。
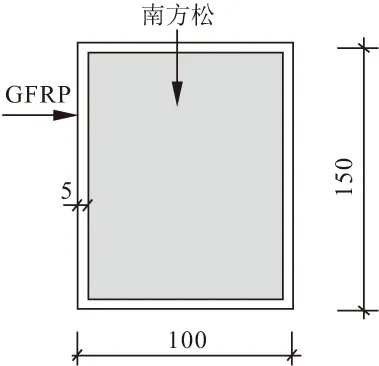
图1 梁柱截面示意/mm
设置加劲肋顶底角钢如图2所示,其中梁上侧角钢定义为顶角钢,下侧定义为底角钢,梁侧钢肢定义为长肢,柱侧钢肢定义为短肢。本试验中所有角钢和加劲肋均采用Q235B级钢材,厚度均为8 mm,加劲肋两边长均为100 mm,试件中所有焊缝为一级焊缝。L1表示长肢螺杆孔中心到底部的长度,其余已表示尺寸6个角钢均一致。
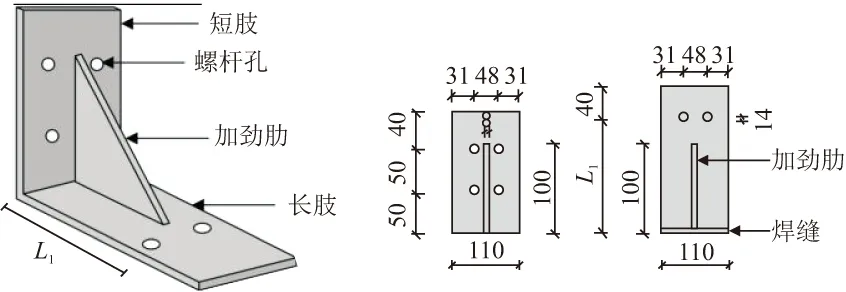
图2 顶底角钢截面/mm
木芯复合材料构件通过6个直径14 mm长220 mm的普通螺杆与顶底角钢相连,形成木芯复合材料梁柱T形节点试件。试件尺寸见表1。
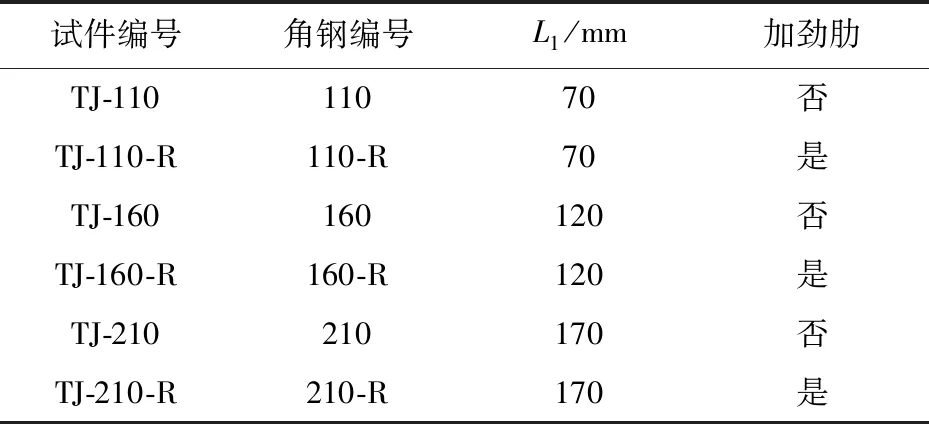
表1 试件尺寸
1.2 材料性能
根据文献[9,10]中的测试方法,可测得本试验GFRP面层的抗压、抗拉强度及弹性模量;根据文献[11,12]中的测试方法,可测得本试验所用南方松芯材的抗压、抗拉强度及弹性模量,见表2。根据文献[13],测得所用螺杆及角钢的力学性能,见表3。

表2 GFRP与南方松的力学性能

表3 钢材的力学性能
1.3 测量方案与加载装置
采用静力加载方式进行加载试验,根据T型节点的实际受力特点,参考文献[7,8]的实验方法,确定本实验的具体试验方案,如图3所示。T形节点安装在竖直平面内,复合材料夹芯柱上下两端分别通过钢套筒与反力架相连。夹芯梁保持水平,加载点位于梁上表面,距离梁柱交界处400 mm,轴向压力由1000 kN压力机提供,加载速度为2 mm/min。
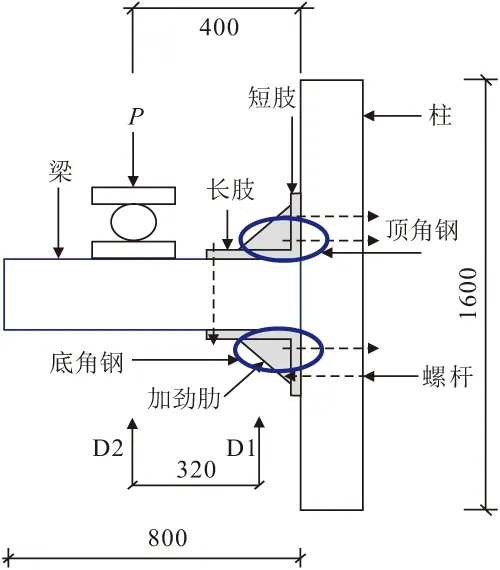
图3 加载装置示意/mm
在与梁柱交界处和加载点下端各设置一个位移计,编号D1和D2,用于测量夹芯梁在测点处位移。其中梁柱之间的相对转角θ可表示为:
θ≈tanθ=(Δ2-Δ1)/a
(1)
式中:Δ1,Δ2分别为位移计D1,D2的位移值;a为集中荷载P与梁柱交界面之间的距离。
在角钢长短肢上布置应变片,如图4所示。
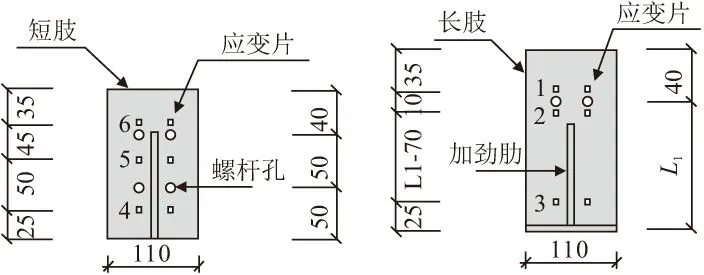
图4 测点布置/mm
2 试验结果与分析
2.1 破坏模式
在静载试验中,6个添加不同顶底角钢的木芯复合材料T形梁柱节点表现出不同的破坏模式,具体可以总结为以下三种:
(1)角钢屈服破坏
试件TJ-110,TJ-160,TJ-210均发生角钢屈服破坏。加载过程中,由于节点处存在较大弯矩,梁端连接处截面上侧受拉,下侧受压,导致顶角钢长肢受到向左的拉力,使角钢转角处与柱发生分离,分离间隙随荷载持续增大。底角钢由于梁柱转角的不断增大,长肢开始出现向下的弯曲变形。以试件TJ-160为例,顶角钢转角处应变随荷载持续增大,当顶角钢短肢明显被拉离柱表面时,转角处应变值为1122.81×10-6,超过其屈服应变,角钢屈服。试件最终的破坏表现为角钢转角处的全截面屈服,如见图5所示。

图5 角钢屈服破坏
(2)夹芯梁局部压溃破坏
试件TJ-110-R与TJ-160-R表现为木芯复合材料梁局部压溃破坏。与前述无加劲顶底角钢T形节点相同,顶角钢长肢受到向左的拉力,从而使角钢转角处存在与柱表面发生分离的趋势。但由于加劲肋的约束,顶角钢短肢与柱表面分离缓慢。底角钢由于加劲肋的设置,底角钢长肢上弯曲点从底角钢转角处移到加劲肋边缘。木芯复合材料梁分别在顶、底角钢长肢上出现两个局部受压区,且底角钢局部受压区面积较大。梁下侧局部受压强度随着变形的增大而不断增大,当荷载增大至木芯复合材料梁局部承压强度时,底角钢短肢端部木芯复合材料梁因为应力集中而导致局部被压溃,在压溃区域左右两侧出现较大的相对变形,变形使面层GFRP受剪而出现剪切裂纹。裂纹垂直于底面向梁上面发展,到梁中和轴位置裂纹向梁柱交界处转向,并向交界处不断发展。继续加载,试件最终表现为梁下侧受压区的局部压溃破坏,而上部由于持续加载时间过长,梁受压区芯材被挤出,如图6所示。

图6 局部压溃破坏
(3)螺杆拉断破坏
试件TJ-210-R表现为螺杆的拉断破坏。木芯复合材料梁在外力P作用下,产生向下的转动,底角钢长肢发生弯曲变形,随着荷载的增加,底角钢的弯曲变形通过螺杆传递至顶角钢。顶角钢在螺杆拉力作用下,长肢上加劲肋边缘开始出现沿加载方向的弯曲,加劲肋边缘的应变值不断增大。荷载的增加使底角钢下侧木芯复合材料梁变形增大,局部承压面积变大,受压区复合材料梁未发生局部压溃破坏,螺杆已达到极限抗拉承载力,试件出现螺杆拉断的脆性破坏,此时顶底角钢长肢的加劲肋边缘应变值小于钢材的屈服应变,试件破坏模式受螺杆极限抗拉承载力的影响,如图7所示。

图7 螺杆拉断破坏
2.2 弯矩-转角
试验实测T形节点弯矩-转角曲线见图8,由图8可知,加载前期曲线基本呈线性发展,在经历非线性的屈服平台后,后期塑性发展阶段近似为一条直线。塑性发展阶段,试件TJ-210-R的塑性由螺杆的塑性所决定,当试件发生螺杆拉断时,曲线中TJ-210-R的塑性发展段较短。试件破坏之后,6组试件承载力迅速下降到峰值荷载的20%~30%,故曲线只给出了试件最终的破坏点。
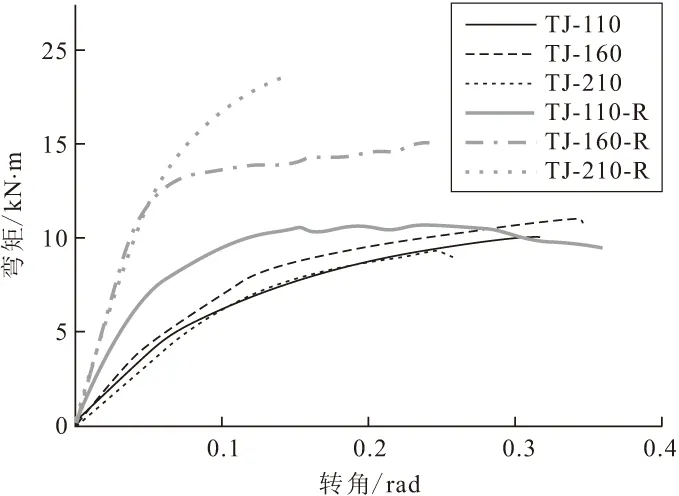
图8 弯矩-转角曲线
对于此种没有明显转折点的弯矩-转角曲线,本文采用文献[14]的“最远点”法(曲线上距离峰值点与原点连线最远的点,定义为屈服点。当曲线上有多个点时,则取这些点荷载值的平均值,对应到曲线上则为屈服点,具体如图9所示)来确定节点的屈服弯矩。该方法简单易于操作,编程计算更可避免人工取值导致的计算差别,且由该方法确定的屈服点作为拐点,所得双折线下面积与原曲线下面积最为接近,即变形能最为接近。
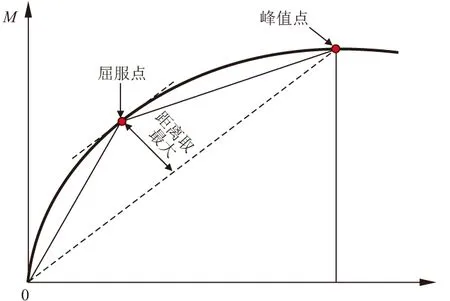
图9 最远点法定义屈服点
单调加载试验结果见表4。
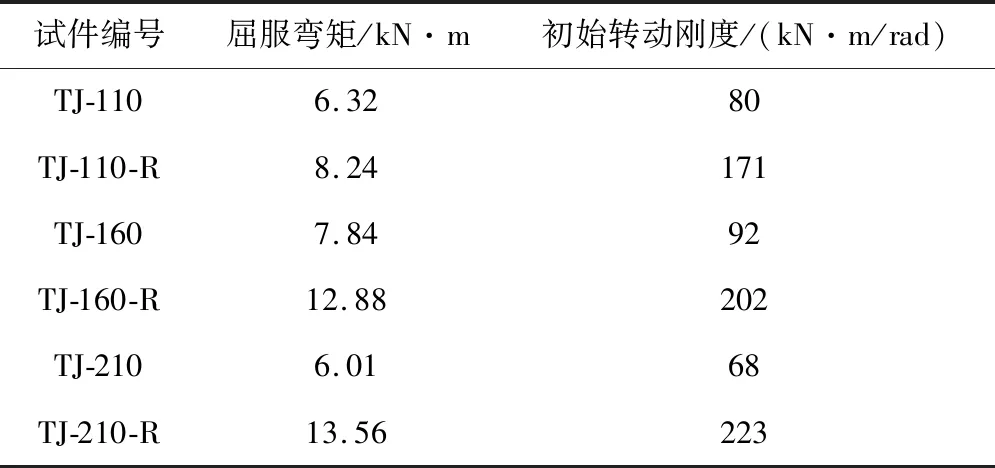
表4 单调加载试验结果
由表4可知,设置加劲肋顶底角钢T形节点试件,节点的屈服弯矩有较大提高。例如试件TJ-110-R比试件TJ-110、试件TJ-160-R比试件TJ-160、试件TJ-210-R比试件TJ-210分别提高了30.38%,64.29%,125.62%,由此可知加劲肋的设置改变了节点的破坏模式,无加劲肋顶底角钢的节点试件宏观的非线性屈服是由于角钢屈服所导致的;而设置加劲肋顶底角钢的节点试件宏观的非线性屈服是由于夹芯梁的局部压溃或者螺杆拉断引起的;前者的承载能力明显小于后者,所以设置加劲肋顶底角钢节点试件的屈服承载力高于无加劲肋顶底角钢节点试件。
2.3 节点初始转动刚度
取初始节点的切线斜率作为节点的初始转动刚度,试验结果见表4。试件TJ-110与TJ-110-R对比,TJ-160与TJ-160-R对比,TJ-210与TJ-210-R对比,后者的初始转动刚度分别提高了113.75%,119.56%,227.94%,说明设置加劲肋的顶底角钢对节点的转动起到明显的约束作用,可以有效提高节点的初始刚度,且加劲肋长度一定的情况下,顶底角钢长肢越长,初始转动刚度越大。对于未设置加劲肋顶底角钢的节点试件,不同长肢肢长对初始转动刚度的影响不大。
3 承载力计算与试验值比较
3.1 角钢屈服破坏
在未设置加劲肋顶底角钢T形节点试件中,当角钢厚度相对于螺杆直径较薄时,角钢的受弯肢上会出现塑性绞线,文献[15]中提出了考虑螺杆直径影响的受弯杆的简化计算方法,此方法认为螺杆中心附近角钢出现全截面屈服,与计算有关的下角标t和s分别表示顶部角钢和底部角钢。
TT1=Mpl.Rd(4n-ew)/[2mn-ew(m+n)]
(2)
Q=Tm/(2n)
(3)
(4)
ew=dw/4
(5)
式中:dw为螺母的直径;ba为角钢宽度;tt为顶角钢钢材厚度;T为撬力;fy为本文所用钢材屈服强度,具体见表3;n为自由端到螺杆中心点距离,m为角钢的有效受弯高度。计算简图见图10。文献[15]中关于有效螺杆间距的计算公式为:
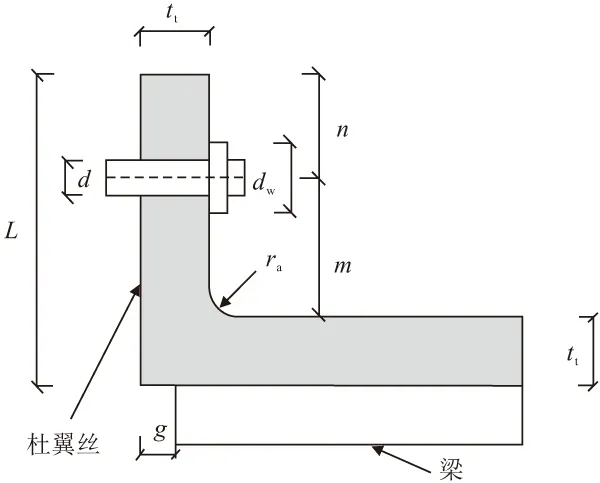
图10 m计算示意
(6)
式中:g为木芯梁到柱翼缘的距离。
3.2 梁局部压溃破坏
在设置加劲肋顶底角钢T形节点试件中,梁下侧出现受压区出现复合材料梁局部压溃现象。根据试验现象及破坏模式,将木芯复合材料梁作为隔离体建立力学模型,进行受力分析,计算简图见图11,采用以下基本假设。
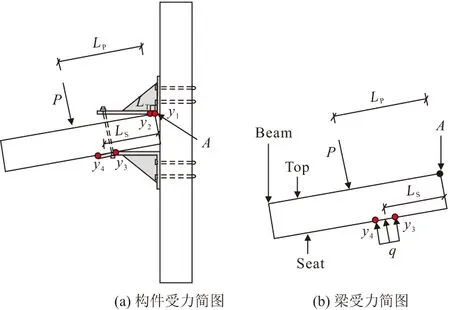
图11 承载力计算简图
(1)外荷载P距梁端底面距离一定(LP=400 mm),不考虑梁柱转角引起力矩的缩小,并始终垂直作用于梁上表面。
(2)梁上表面与顶角钢长肢接触的局部受压面积较小,不考虑此部分合力影响,并简化其作用点为A。
(3)梁转动角度较小,不考虑转动引起的力矩减小,取合力作用点到梁底端距离Ls为合力作用力矩。
3.2.1 低碳绿色材料的应用 在绿道规划设计中,采用多种绿色手段与生态建设方法,尽可能实现绿道的低碳减排,将废弃材料以新的设计语言呈现,使之得以在绿道景观中重生。如利用绿道内废弃构筑物为基础建造景观建筑、利用场地废弃枕木、山崖剥落的岩石等作为场地铺装,以及利用湖中枯木造景、废弃轮胎等打造景观小品等。
对A点列力矩平衡方程,得
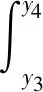
(7)
式中:b为木芯梁截面宽度;LP为外力P到A点的力矩;Ls为底角钢受压侧合力点到A点力矩;q为木芯复合材料梁下表面局部受压区的法向压力。
由于计算中需知道受压区木芯复合材料梁的压应力合力大小以及作用点位置,为进一步简化,采用等效矩形应力图来代替理论应力图形。分别对木芯复合材料梁受压区合力和截面弯矩进行等效处理,等效后木芯复合材料梁受压区合力大小相等、合力作用点位置保持不变。计算简图见图12。
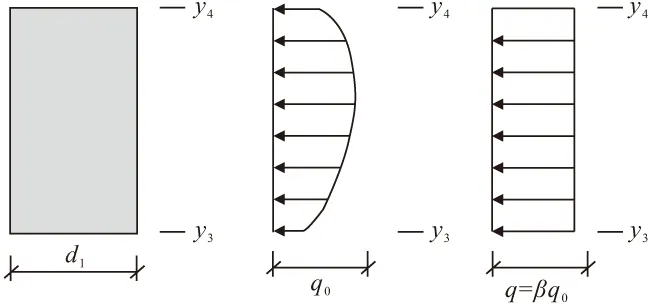
图12 等效受压区计算简图
q=βq0
(8)
式中:β为荷载不均匀系数,与木芯复合材料梁和角钢接触面的压应力分布有关。
图11中:y1与y2分别为木芯复合材料梁上表面受压区边界,本节在基本假设2中,不考虑此部分的影响;图12中:y4与y3为木芯复合材料梁下表面受压区边界;Lc为添加加劲顶底角钢节点试件实际受压长度,TJ-110-R,TJ-160-R,TJ-210-R的Lc长度分别为36.0,41.2,46.1 mm;d1为木芯复合材料梁高(100 mm)。
梁下侧受压区合力作用点到A点的力矩Ls可表示为:
Ls=L1+L2-Lc/2
(9)
式中:L1为角钢根部到长肢螺杆孔中心线的距离;L2为长肢上螺杆孔中心线距自由边的长度,本文为40 mm;Lc为底角钢长肢所测量的受压区的长度。
3.3 螺杆拉断破坏
当连接处木芯复合材料梁受压区面积较大时,梁未发生局部压溃破坏,节点承载力由螺杆的极限抗拉承载力决定,单个螺杆的最大拉力Fb可表示为:
(10)
Fb=nbBn
(11)
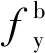
3.4 结果比较
最终的求解结果见表5,试验值与计算值吻合较好,最大相差10%。
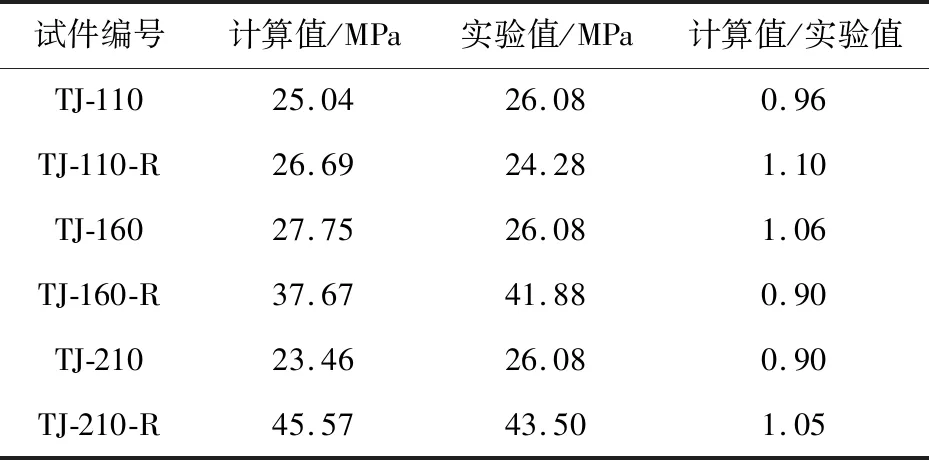
表5 极限承载力计算值与试验值比较
4 结 论
(1)静力加载状态下,设置顶底角钢连接的木芯复合材料梁柱T形节点主要发生三种破坏,分别为:角钢屈服破坏、木芯复合材料梁局部压溃破坏以及长肢上螺杆的拉断破坏;
(2)与不设置加劲肋顶底角钢T形节点相比,添加加劲肋的试件可显著提高节点承载力和初始转动刚度;
(3)对于采用顶底角钢连接的木芯复合材料梁柱T形节点,本文提出的承载力计算公式具有较好的预测能力,计算值与试验结果吻合较好。
