复杂曲面参数化设计方法——以月亮湾城市阳台为例

张 慎，辜文飞，刘 武，王海亮

(1.中南建筑设计院股份有限公司，湖北 武汉 430071；2.武汉城市铁路建设投资开发有限责任公司，湖北 武汉 430061)

随着数字化技术在设计领域的普遍应用，建筑结构方案变得日益新颖奇特，出现大量的非线性造型。非线性曲面从方案深化至建筑产品生产的过程中，往往涉及大量需要效率和精确性的重复工作，引入参数化设计将在此过程中发挥重要作用。

参数化设计是目前新兴设计方法的抽象概述，包括生成设计、算法集合、关联性模型等核心概念，其优势在于对信息的集成与逻辑分析[1]。在参数化设计的过程中，将全部设计要素作为某个函数的变量，通过设计函数或者算法将相关变量关联起来，实现输入参数便可自动生成模型[2]。方案深化是形体元素重新排列组合不断找寻的过程[3]，由于其不可预知性，在深化时确立总体原则后，具体的细节要求和条件均会随着深化过程而发生变化[4]，但如果采用参数化设计，可显著减少方案调整中获得反馈和决策后重复绘制过程所需的时间，降低反复绘制时人为造成的难以避免的不精确性。

通过参数化设计，设计师可以快速构建高精度数字化的复杂曲面表皮，并在模型关键参数间建立联动关系，实现对复杂曲面的优化重构和方案比选。参数化的复杂曲面可以实现图形化渐变及表皮动态化，比手工建模时模糊的调整更加精确，更具有逻辑性[5～8]。在传统方法无法应对修改调整带来的大量返工时，采用参数化设计可提高设计修改效率[9]。

参数化设计正是当前研究的热点，国内外建筑设计中均引入参数化设计进行实践探索。国内大型建筑设计也开展了部分实践。如北京凤凰国际传媒中心采用参数化设计，对建筑方案进行整体设计控制，实现建筑、结构以及幕墙表皮的统一。杭州奥体中心使用参数化设计对网壳主体进行描述，确定曲面形态，有效实现表皮网格划分[10]。本文介绍了复杂曲面参数化设计的基本流程，并提出一种曲面重构方法，并将该方案应用于武汉月亮湾城市阳台工程实例，完成复杂曲面的设计深化和施工配合等任务。

1 复杂曲面参数化优化方法

1.1 曲面参数化设计流程

参数化设计将设计过程通过逻辑链重新组织，在初步确定设计意向后，把建模分解成通过有限参数控制的造型形状，加入规范、规则等限定条件辅助判断。在获得结果反馈时进行人工判断，以此决定是否修改参数、修改建模逻辑、或者修改设计意向。

复杂曲面参数化设计需要充分考虑优化目标、基本变量、约束条件和算法(见图1)。在曲面优化之前需要对设计需求进行分析，基于优化目标确定曲面优化的基本变量、约束条件。分析基本变量与约束条件和优化目标之间的关系，确定优化算法。优化目标直接控制整个参数化设计过程。

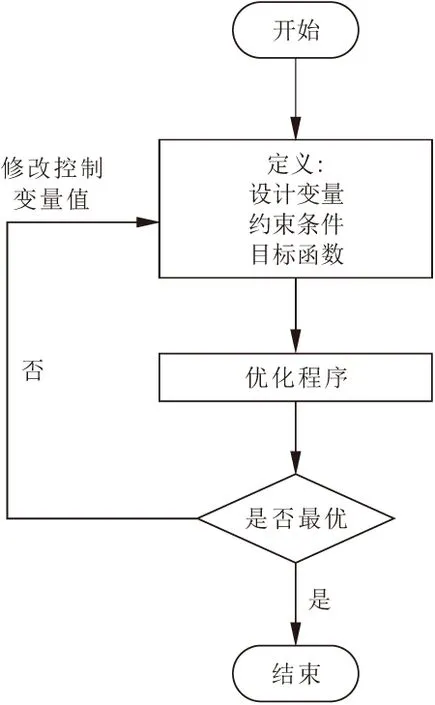
图1 曲面参数化设计流程

1.2 曲面重构

复杂曲面一般为自由曲面，无法用数学解析公式表达。借助参数化设计平台，可以实现对复杂曲面几何变化进行理性分析和设定，从几何学的角度对复杂曲面进行拟合重构。整个重构过程遵循参数化、数据化和可视化紧密结合的原则。参数化曲面重构的基本步骤如图2所示。

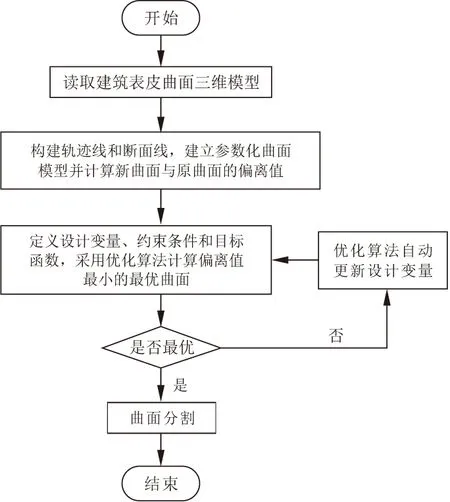
图2 参数化重构曲面

(1)读取设计师提供的待优化复杂曲面建筑表皮的三维模型。

(2)构建两条相交的控制曲线，并利用控制曲线参数化生成一个新曲面。

(3)计算新曲面与原曲面的偏离值。通过约束条件和优化目标判断是否满足曲面重构要求。

(4)采用优化算法调整控制曲线的形状，不断进行迭代，直至出现满足优化目标的曲面停止迭代。

(5)提取原曲面的边界线，沿新曲面法向拉回到新曲面，并对新曲面进行切割。

(6)切割后得到的曲面视为最优曲面。

自由曲面可采用NURBS表达式表达。对于NURBS曲线或曲面，控制点坐标和权因子是影响曲线或曲面形状的主要参数。在步骤2中通过修改控制曲线的形状达到修改控制点坐标和权因子的目的，进而控制曲面的形状。在构件控制曲线(轨迹线和断面线)的过程中，要控制曲线的长度以保证能生成覆盖原曲面的新曲面。

为对比新曲面与原曲面的形状偏差，在原曲面上提取m个采样点，计算采样点到新曲面的最小距离，对这些距离值取平均视为曲面的偏离值。曲面的偏离值越小，表明两曲面偏差越小，对曲面形状的改变越少。在步骤3中通过设置采样点的个数m来实现对拟合精度的控制，m值越大，采样点越密集，误差分析精度越高。

2 曲面参数化设计的应用

大量非线性建筑的出现，赋予了建筑新的美学意义，但同时也给设计施工带来了相当大的难题。借助参数化设计平台，可以实现对复杂曲面有理化分析，包括从几何学的角度对曲面的平面和三维空间生成进行准确的定义和呈现。通过参数化设计在项目关键参数之间建立联动关系，设计师可快速构建高精度的复杂曲面，参数化控制曲面形式、大小和逻辑，参数化控制曲面数据输出。

2.1 曲面简化

随着复杂异形建筑的大量涌现，异形幕墙也大量出现。在建造施工过程中，建筑幕墙会被离散成平板、单曲面板和双曲面板，再由这些板块拼接拟合而成。双曲面板具有加工难度大、加工成本高、施工安装难度大等特点。为了满足施工要求和降低工程造价，在设计过程中应尽量减少双曲面的出现。

复杂曲面参数化设计给双曲面优化成单曲面带来可能。在幕墙板块划分前，基于优化目标对建筑曲面进行优化处理。基于优化后的曲面直接分割成单曲面板块，可实现用单曲面板拟合双曲面建筑表皮的目的，同时能更好消除板块之间的翘曲缝隙。

2.2 曲面模数化

除异形幕墙外，复杂异形建筑中还存在大量其他造型。这些复杂曲面大小、翘曲度和形式都存在一定的差异，在加工制造过程中需要采用大量的模板，会带来较高的加工成本。

通过参数化曲面优化技术，设计师再通过优化算法将大量的复杂曲面进行拟合和归并，减少曲面的种类数，进而减少模板的数量。模具的减少和反复使用既能节约加工特定模具的成本，也能加快加工制造的速度[11,12]。

2.3 参数化输出加工数据

在完成参数化设计后，设计师可利用参数化平台以表格、图纸等形式输出加工数据，提高复杂曲面的定位精度和加工精度(见图3)。利用参数化输出加工数据既提高了设计效率和制作速度，又保证了数据的精确性。

图3 参数化输出台阶图纸

3 工程实例

武汉月亮湾城市阳台坐落于武昌生态文化长廊上，旨在打造武汉城市景观，提高长江主轴的可识别度。本工程为绿化及阳台工程，包括平台景观和平台层以下建筑，平台景观面积为124588 m2，平台以下建筑面积49922 m2，建筑效果图如图4所示。

图4 设计效果图

本工程设计目的在于城市景观、交通环境的提升，加强周边居民的交流互动，因此采取了抬高地块地面、重新连接滨江水岸与中央公园景观的设计手段。

因方案抬高地面，所以在人行出入口处存在较大的高差。在出入口的室外景观台阶处，形成了加工和深化难度较高的复杂曲面，如图5所示。

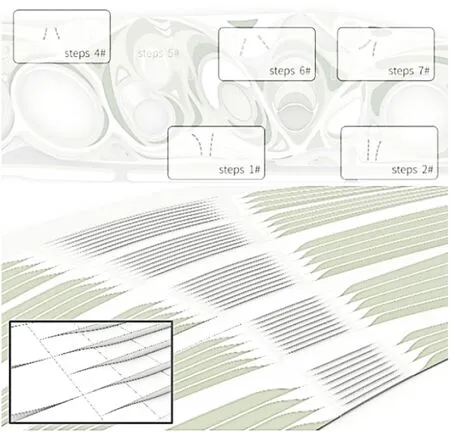
图5 室外景观台阶实例

3.1 项目难点

本方案在人行出入口处有5组图示类型中表示的景观台阶组合，每个台阶组合的两侧均有一段直纹曲面，用于衔接过渡平直的踏步段曲面与倾斜的草坪段曲面。由于踏步段与草坪段边缘在平面坐标内的方向沿着景观台阶边缘一直在变化，使得每段过渡段直纹曲面的形状均略有不同，如使用混凝土现浇后在表层制作水磨石面层，制作难度太大且无法保证建筑效果，故决定将直纹曲面过渡段(下文简称过渡面)做成预制构件。

台阶合计有19段，每段台阶有大致8～10级踏步，粗略估计预制构件总数约400个，开模难度大，造价高。为降低施工难度和成本，在原方案的基础上进行曲面优化，减少复杂曲面的种类从而减少预制构件的种类，降低项目成本。

采用传统手动方式进行调整存在一定困难。首先无法预测哪一种规格尺寸能尽量多的满足整段台阶的拟合；其次即使将同一个规格的预制构件建模出来，如何复制与定位也将面临精确性的挑战；另外，完成预制构件的定位后，与预制构件的过渡面相连的踏步段曲面和草坪段曲面也应逐级建模。当建模完成之后如果整体效果不理想，需要进行造型调整，则前述的工作都需从头再来。

3.2 解决方案

3.2.1 确立设计要求

通过对过渡面周边条件进行分析，确定过渡面处深化设计的约束条件如下：

(1)预制构件的形状应尽量精简，便于加工，预制构件形状的总数量尽可能减少。

(2)遵守边线，保持台阶的总体形状的流畅连续。

(3)每两级踏步与草坪相连的部分应为平段以方便草坪处的混凝土造型。

(4)台阶段与台阶段之间的夹角由两部分构成：

1)预制构件非矩形时，每级踏步均有夹角；

2)台阶段之间形成夹角。

(5)深化过程中应注意休息平台宽度应满足规范要求等。

本实例最终的深化流程图如图6所示。

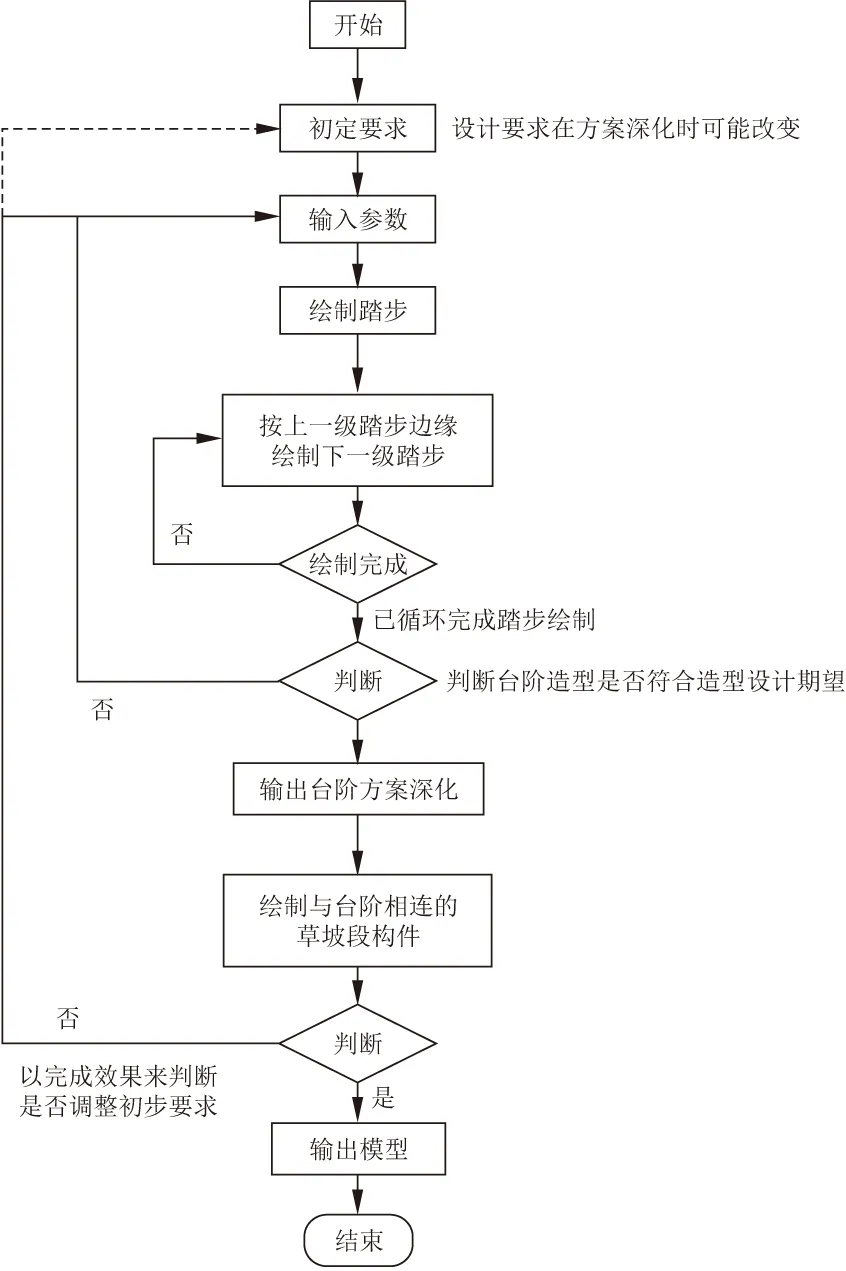
图6 深化流程

3.2.2 分析构件

分析原设计方案的楼梯边线形状，明确设计意图后，重新绘制出一条流畅的边线，以此作为使过渡面预制构件对齐的深化条件，绘制的边线(arc)如图7所示。该曲线的流畅度可由设计者的感官体验确定，也可通过数个特征点，形成内插点曲线，由设计者选择带有指向性的“主观”构建参数[11](如点的坐标值，或者由两个自定义向量blend形成曲线)。

分析预制构件模块，为方便加工而尽量精简。故如图8所示，设∠A1，∠A2为直角，利用A1B1与A2B2两边边长的调节，获得预制构件在楼梯中排列时的夹角。指定一段A1A2作为梯段起点，令A1点落在边线arc上。

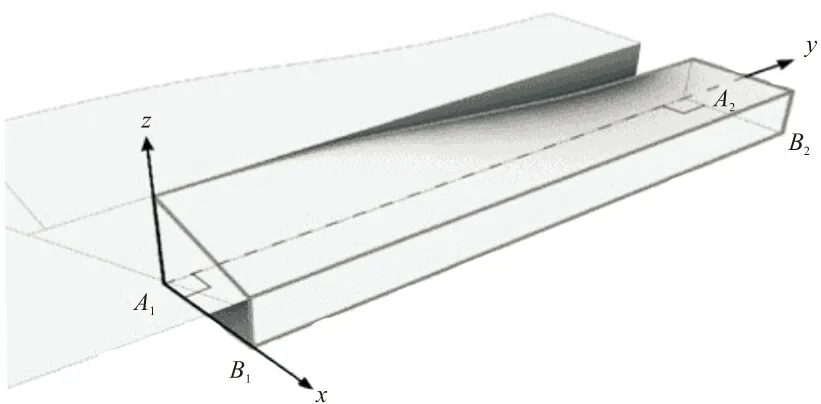
图8 分析预制构件模块

3.2.3 参数化控制设计

在Grasshopper中导入边线arc，将A1A2，A1B1与A2B2边线长度设定为参数，通过Number Slider输入。在A1与A2点处求得垂直于线段A1A2的参考面。通过分解参考面，可以获得向量A1B1与A2B2，利用Line SDL加入边线长度参数即可获得A1B1与A2B2线段。连接已求得的A1，B1，A2，B2四点可求出第一级踏步的平面轮廓。

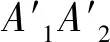
传统方法的重复操作将会浪费大量时间，而且在操作过程中容易导致误差累积，故重复过程采用循环工具完成。在本项目中使用的是Anemone工具，使用方法类似于编程语言中的for循环(如图9所示)：将一对电池Loop Start和Loop End相连形成逻辑语句，在N端输入循环次数(作为遍历条件)，D0(Dn)端输入需要循环的内容，语句中间加入自定义的函数fx(参数化设计流程)，在Loop End处设置记录数据，最后修改T端的数据(通常使用Toggle开关)，运行结束后在最右侧拿到循环结果。通过此循环电池的设置，可自动循环绘制完所有踏步的平面轮廓。

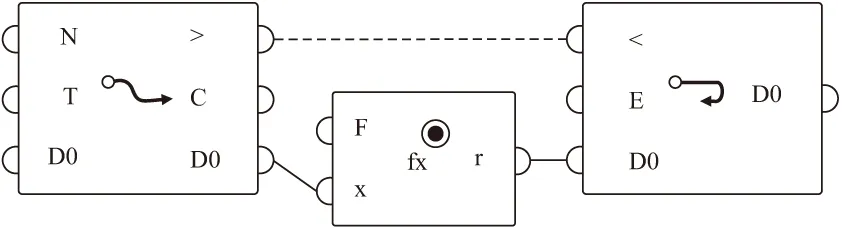
图9 Anemone电池使用方式

3.2.4 利用参数化工具实现自动建模

通过上一步获得的平面，加入踏步高度参数h，即可获得本次优化需要得到的预制构件。将A1A2线段升高p(p为预制构件A2B2边线处厚度)，等分一定数量的点，将靠近A1处的点继续升高h，通过升高后的点绘制整段曲线，放样后可求得预制构件的直纹曲面上表面。

通过设置参数将边线arc偏移一段距离，延长预制构件上表面的两条长边，获得交点，筛选出每两级踏步对应的交点，按顺序连成直线，与预制构件上表面放样可得草坪相连的混凝土曲面。

两段预制构件之间提供步行功能的踏步段，可利用两侧预制构件的定位线进行blend操作，求出所有边线后通过loft求得(对截面进行sweep扫略的方法不利于控制边线)。

预制构件和踏步段的顶面需要进一步加工以加入灯槽。采用对预制构件的直纹曲面上表面切割求出定位线，通过放样获取灯槽的形体后，用布尔运算从预制构件和踏步段面形体中做减法，即可实现灯槽的建模。

所有的几何模型形体在最终完成时均可使用布尔运算组合成单一物体。如果布尔运算获得的结果不正确，应检查几何模型的面是否反向(检查方法为查看体积是否为负数)，不正确的几何体可Deconstruct Brep分解形体后再重新组合进行修正。

3.2.5 调整参数以完成模型

原方案中，过渡面处的踏步尺寸范围包括踏步深320～680 mm，踏步高为130 mm和150 mm。预制构件越长，则楼梯现浇部分越短，越利于建造。通过多次参数调整，确立预制构件的长度A1A2为1.8 m时能保证所有楼梯段的曲线顺滑。另外，由于5组台阶形状之间差距较大，故每组台阶如采用同一种尺寸的预制构件可做到总种类数目最少，但考虑到台阶左右两侧预制构件不能混用，因此以10种预制构件类型调整参数。将10种预制构件类型的相似长宽归并后，最终确定7种类型。

3.2.6 输出模型

当模型完成后，烘培(bake)出模型体量后即可导入Revit中，并指定材质等参数。在参数化平台指定导出时，可利用图层命名、颜色、分组等多种方式进行管理，方便后续操作。烘培得到的预制构件数字模型可直接交予工厂进行模具加工深化和制作，如图10，11所示。

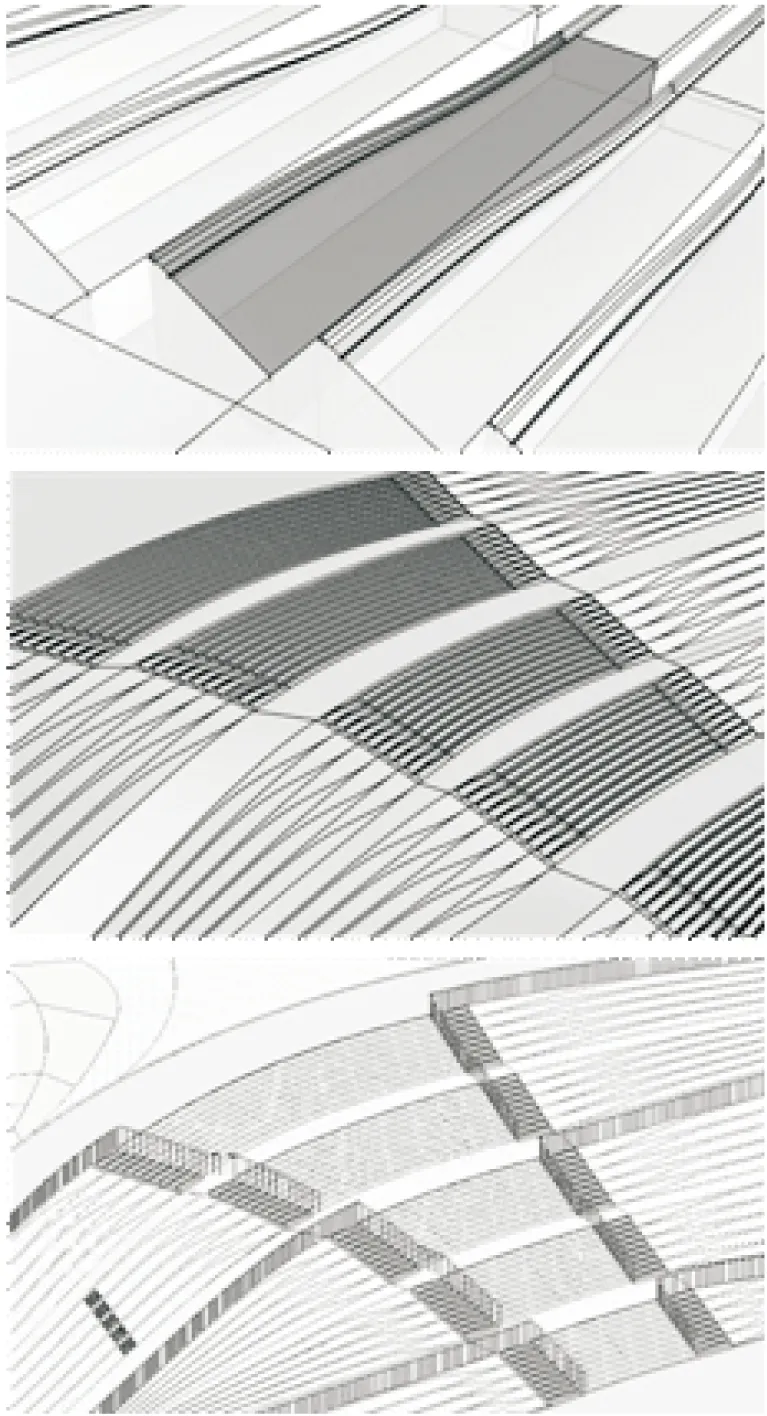
图10 模型输出

图11 预制构件制作

3.2.7 分析总结

此次设计案例的优化方案将原有预计400种不同规格的预制构件简化为7种，大幅节约了模具制造的成本，按模具开模费用2万元计算，仅开模项的精简带来的直接经济效益为节省费用约700万元。

在后续的设计工作中，该模型可导入Revit，实现模型和图纸的深化；在施工过程中也可以使用模具在参数化平台中的定位数据，直接用于现场放样定位工作，方便后续的施工[13]。

4 结 论

方案设计和深化是一个经验性导向的设计过程，建筑设计师主要通过穷举的方式进行试错，通常先假想方案，然后在深化时不断匹配设计条件，在得到阶段性成果后进行适当的修改，从而得到满意的结果。

本文运用参数化设计有利于穷举法的尝试，通过设置合适的参数，控制变形的范围，可以在短时间内获得大量的阶段性成果以利于决策，甚至可以在明确设计目标时，将优化目的以数据描述，通过迭代等优化算法自动调整输入参数，以此迅速获得合理解。

通过武汉月亮湾城市阳台复杂曲面参数化设计的实际案例，本文展示了利用参数化设计达到设计辅助和控制的案例成果，主要结论如下：

(1)利用Rhino+Grasshopper平台的可视化建模编程的特点，通过对参数的控制和编程项的简单调整，可以获得快速反馈的优势，从而促进设计的决策效率，在面对颠覆性方案修改时对原有程序做小的修改就能满足新条件。

(2)参数化平台提供强大的可扩充性，可利用第三方插件或者C#/Python等编程手段实现自定义插件，有助于实现复杂曲面参数化设计。

(3)参数化设计在建模过程中体现了比传统方法建模更好的精确性，在复杂曲面的设计中有很大的作用，结合BIM技术能带来更高层次的变革和创新。