基于EFAST法的公路梁桥全局敏感性分析

张敬雷，王 伟，李 彤，罗 辉

(1.中国铁路总公司工程质量监督管理局，北京 100844；2.保利(武汉)房地产开发有限公司，湖北 武汉 430040；3.华中科技大学 土木工程与力学学院，湖北 武汉 430074)

敏感性分析可定义为分析模型输入的不确定性对其输出不确定性的影响[1]。桥梁结构形式多种多样，荷载作用五花八门，同时在施工、运营、维修等各个不同阶段具有不同的受力特点与分析重点，兼之其服役时间长需考虑到耐久性，分布地域广需考虑到环境影响，即模型复杂多变，输入因素广泛。因此针对不同分析目标的桥梁敏感性长时间以来都是研究热点。

静力分析方面，王疆[2]选取连续梁桥，对混凝土重量、温度变化及预应力等输入参数与多个施工控制指标间的敏感性进行了分析，但每次仅改变一个因素，即采用单因素敏感性分析；Li等[3]则采用随机有限元法，结合神经网络对悬索桥的静力响应进行了多元敏感性分析，选取输入输出变量之间的Pearson相关系数作为输入因素对输出因素影响程度的度量指标。动力分析方面，Tao等[4]针对三塔悬索桥在强风作用下的抖振响应，以多调谐质量阻尼器的质量比、阻尼比及频宽比作为影响因素进行了单参数敏感性分析；Zakeri等[5]考虑列车行过水平曲线桥时偏心竖向力和侧向力的激励作用，以行车舒适度为指标，以车桥耦合理论为基础，对铁路超高、列车速度、轨道质量和曲率半径进行了单参数敏感性分析，由此提出了改善行车舒适性的措施。

尽管目前在桥梁敏感性分析方面已有不少研究，但这些研究普遍集中于少量影响因素的局部敏感性分析，且往往不考虑模型的非线性及变量间的交互作用；对于影响因素的不确定性，许多研究采用以某个比例增大或减少的方式，而不考虑变量本身具有概率分布特征。针对以上不足，本文以工程实际中广泛运用的中小跨连续梁桥为例，采用基于方差的扩展傅立叶敏感度检验法(Extended Fourier Amplitude Sensitivity Test，EFAST)进行全局敏感性分析，根据影响因素本身的分布特征进行抽样计算，得到衡量影响因素自身对输出方差贡献的一阶敏感性指标，及包含了与其他因素交互作用对输出方差贡献的高阶敏感性指标，并以此进行排序，指出对结构安全影响重大的因素及可忽略其不确定性的因素。

1 研究方法

1.1 EFAST法

扩展傅立叶敏感度检验法(EFAST)是基于方差的全局敏感性分析法[6]。在傅立叶幅度灵敏性检测法(Fourier Amplitude Sensitivity Test，FAST)的基础上，结合Sobol法方差分解的思想，可以计算一阶及高阶敏感性指标，抽样次数[7]与考虑的影响因素的个数有关，计算量相对较小且具有良好的稳健性。

以Vi表示输入参数xi的方差，Vi,j，Vi,j,m，V1,2,…,k表示输入参数间相互作用的方差，V表示输出总方差，则xi的一阶敏感性指标Si(主效应)为：

(1)

xi与其他输入参数相互作用引起的高阶敏感性指标(交互效应)为：

(2)

则包含xi及其相互作用对总方差贡献之和的总效应STi可表示为：

STi=Si+Si,j+Si,j,m+…+Si,j,…k

(3)

1.2 LSSVM理论

代理模型可以理解为以拟合精度作为约束，通过近似技术对离散数据点进行回归或插值，从而预测未知响应的数学模型。最小二乘向量机(Least Squares Support Vector Machine，LSSVM)将支持向量机(Support Vector Machine，SVM)中的不等式约束改为等式约束，从而将解规划问题变为解线性方程组，达到提高求解速度、降低内存占用的效果；同时将训练样本的误差平方和损失函数作为经验损失，提高了模型的收敛精度[8]，为常用代理模型之一。

LSSVM不局限于线性模型。设样本为n维向量，某区域的N个样本表示为：(x1,y1),(x2,y2),…,(xN,yN)∈Rn×R，通过核函数可将数据从原始空间Rn映射到高维空间φ(xk)，从而将非线性决策函数转化为线性函数：y(x)=ωφ(x)+b。按照结构风险最小化原则，需求解优化问题：

(4)

式中：c为正则化参数；ek为松弛因子；ω，b为系数。引入核函数K(xi,x)=φ(xi)φ(x)=Ωi，采用Lagrange法求解式(4)则有：

(5)

式中：α为拉格朗日乘子。

采用最小二乘法求解式(5)可得：

y(x)=ω·φ(x)+b

(6)

可在MATLAB平台按图1步骤构建模型。

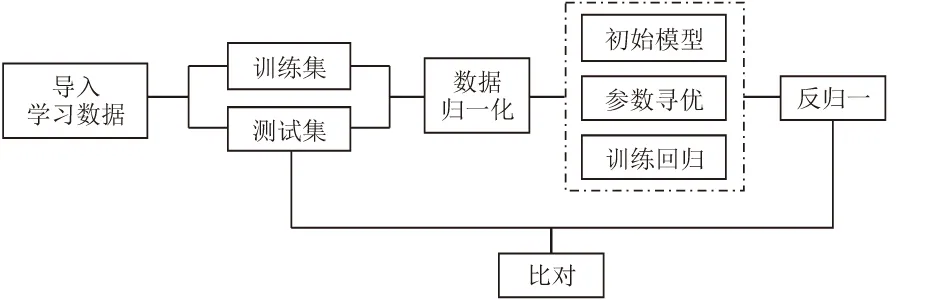
图1 LSSVM建模流程

基于以上理论，首先确定目标变量体系，然后通过有限元法进行初步不确定性计算，生成代理模型学习数据；由代理模型生成整个样本空间所需数据；最后采用EFAST法进行敏感性分析。技术路线如图2所示。

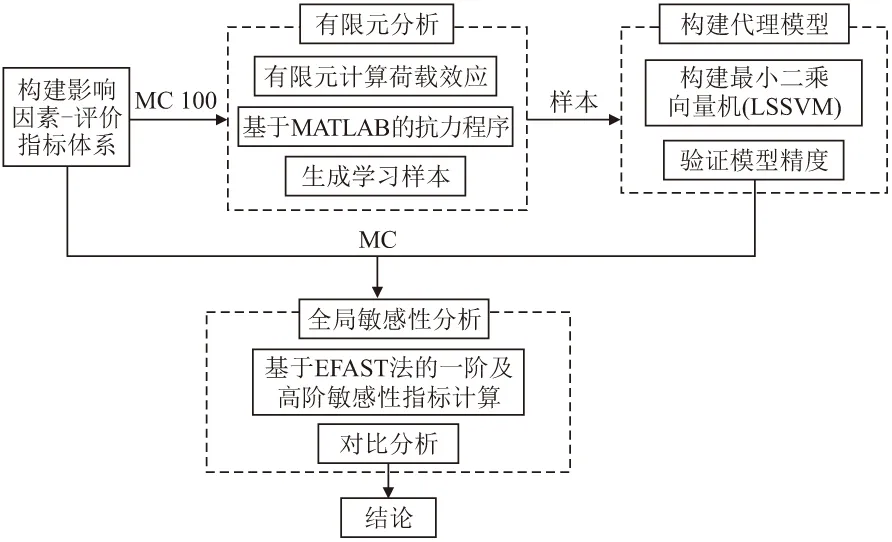
图2 技术路线

2 案例分析

2.1 工程概况

武汉至孝感高速公路上的某宽幅预应力空心板连续梁桥桥面宽度为2×(净12.00+1.00+0.50) m，边跨长24.46 m，中跨长24.40 m。主梁由预制预应力混凝土空心板和现浇混凝土桥面板组合而成，先简支后连续，墩顶负弯矩则由桥面板内普通钢筋承担；每半桥宽主梁含8块空心板，预制梁高1.25 m，组合梁高1.35 m。设计荷载为公路Ⅰ级荷载。

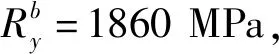
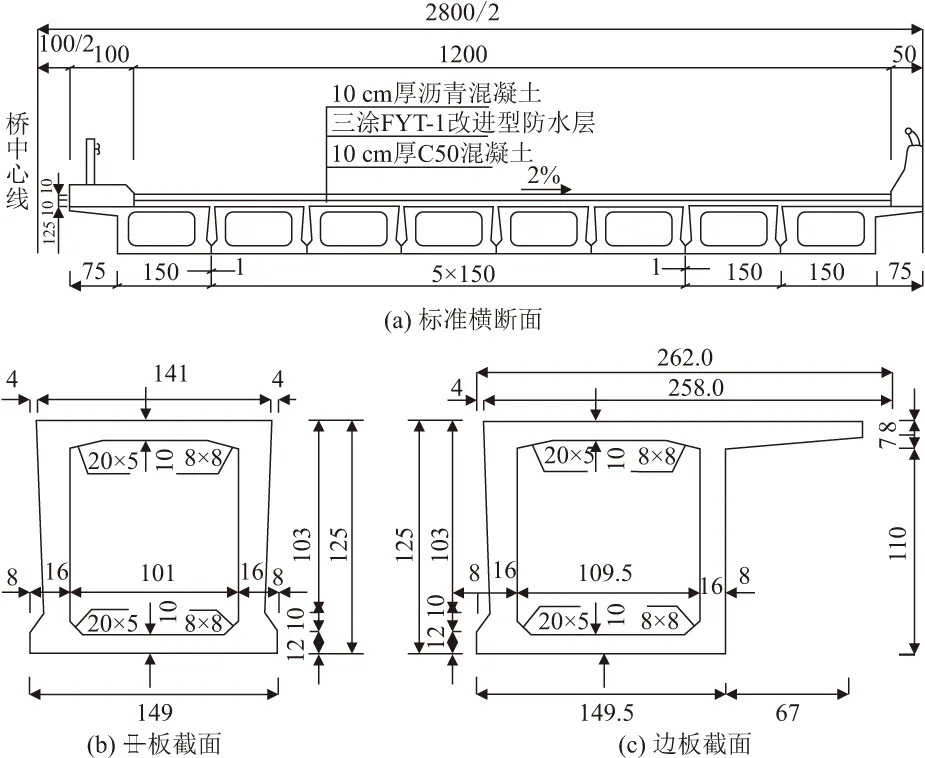
图3 半跨宽桥梁横幅布置/cm

2.2 变量体系

桥梁作为长期使用的复杂结构，其安全性受到自身及外部多种因素影响，例如设计、施工、年久失修、超载、车船撞击及自然灾害等[9]，但桥梁破坏的机理在力学层面上都可以归结为外部作用战胜了结构内在抗力。

本文以连续梁桥成桥后安全性能的敏感性分析为目标，参考可靠度评估中经常涉及的参数，结合结构受力分析的角度，从材料性能、约束强度及荷载作用这三个方面，选取共11个影响因素[10,11]进行不确定分析，将其概率分布特征列入表1。

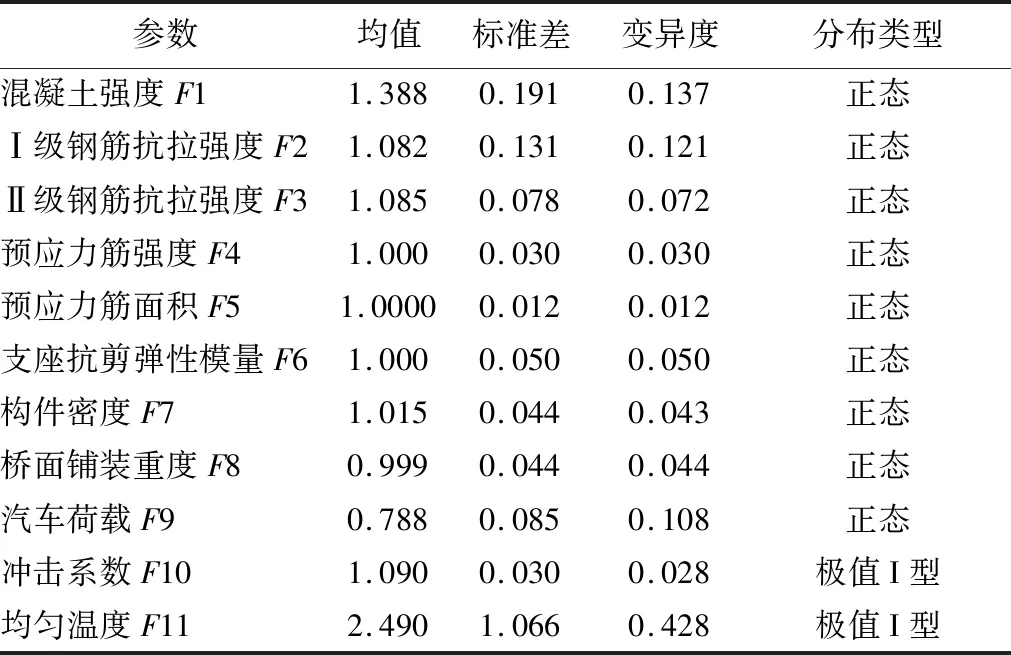
表1 影响因素概率分布特征

参考结构的功能函数表达式定义敏感性分析的评价指标。考虑到构件承载能力极限状态的可靠度计算中，跨中弯曲破坏及支座剪切破坏是极为常用的两种失效模式，定义评价指标Z(M)为单块空心板弯矩最小安全余量，Z(V)为单块空心板剪力最小安全余量，表达公式如下：

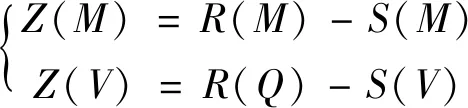
(7)

式中：R(M)，R(Q)分别为单块空心板跨中抗弯承载力及支座处抗剪承载力；S(M)，S(V)分别为单块空心板跨中弯矩最大值与支座剪力最大值。同时，为对梁桥整体状况有所体现，引入挠度安全余量Z(y)：

Z(y)=L/600-y

(8)

式中：L/600取值桥规中跨中挠度允许值；y为每次计算得到的最大挠度。

以上11个影响因素及3个评价指标共同构成敏感性分析的变量体系。

2.3 有限元模型

本文通过大型有限元软件ANSYS，采用实体建模的方式对该桥上部结构进行有限元建模，并进行静力计算。取SOLID65建立钢筋混凝土单元，采用整体式模型，利用实常数组定义普通钢筋的配筋率及钢筋走向；取LINK180作为预应力单元，对其单独进行实体建模，而后通过CEINTF命令与SOLID65单元耦合形成整体，采用降温法施加预应力；取MATRIX27单元模拟板式橡胶支座，定义12×12的刚度矩阵模拟支座各个方向的平动及转动刚度。采用线弹性材料模型，以控制多次运算的计算代价。

对于结构构件与自重，通过添加竖向加速度实现重力荷载；不考虑沥青铺装的刚度，将其作为一个面荷载加载于有限元模型。又由于本文仅对上部结构进行整体静力分析，故汽车荷载可按车道荷载进行加载；取设计车道数为3，荷载等级公路Ⅰ级，采用线荷载的方式，根据设计车道数及车辆荷载横向布置进行加载。

由以上建模过程，得到有限元模型横截面单元划分如图4a所示，将其局部放大则铰缝处构造如图4b所示，任意一跨的预应力筋排布如图4c所示，整体见图4d。

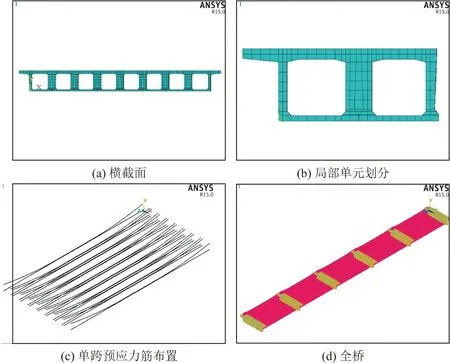
图4 有限元模型

3 敏感性分析

按照表1的概率分布特征，并将变异度分别乘以0.7，1.0，1.3三个系数，对影响因素分别进行100次蒙特卡罗抽样，以探讨变量的离散程度是否对评价指标造成影响。将抽取的样本投入有限元模型计算各个评价指标中的荷载效应值；结合MATLAB，参考JTG 3362—2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》[10]中5.2节相关规定计算各个样本抗力值；由式(7)(8)得到对应的评价指标结果。

将以上有限元计算结果每组取60个样本作为训练样本进行LSSVM建模，每组取40个样本作为测试样本测试模型的有效度。采用有效的LSSVM模型拓展样本数据量，由此进行全局敏感性分析。

3.1 LSSVM拟合结果

为估计LSSVM模型的有效度，参考文献[11]，定义有效度如下：

(9)

(10)

式中：yi为第i个样本的真实值；y′i为第i个样本的测试值；n为测试样本总量；ei为相对误差，M为有效度。按照此定义，可得各组模型有效度如表2所示。

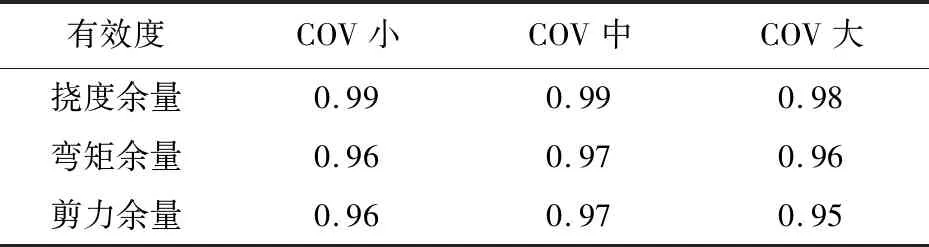
表2 各组LSSVM模型有效度

由表2可见LSSVM均有很好的拟合效果，且以MATLAB的lillitest函数对残差做正态检验，返回值均为0，故结果可信。另以散点图的方式，以影响因素变异度最小状况下的挠度余量指标为例，对LSSVM模型的测试样本真实值与预测值的差异进行比较，可得图5。该图可以直观地反映出真实值与预测值的差值，由图5可见，除了个别异常点，各个情况下的真实值与预测值均非常接近，部分点甚至完全重合，说明代理模型拟合效果优良。

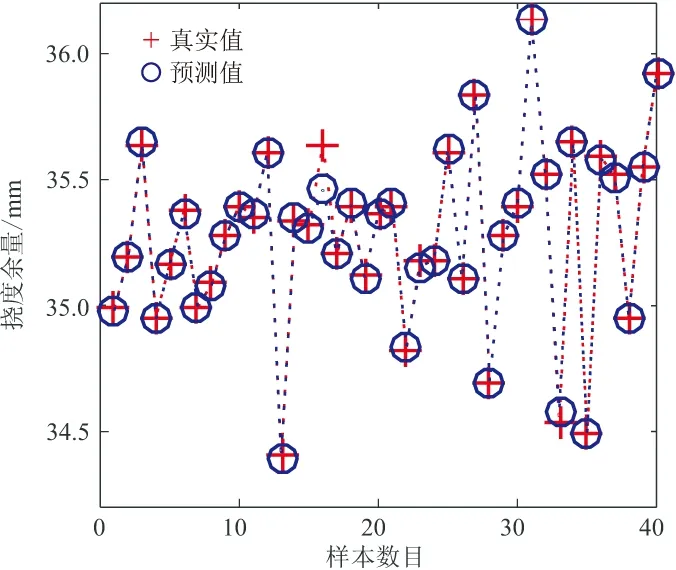
图5 测试样本散点比对

3.2 EFAST全局敏感性分析

结合表1的概率分布特征及EFAST法的抽样要求，在Simlab平台(敏感性分析软件)生成输入参数样本，通过LSSVM模型得到其输出变量，每组1799个样本共生成11组，构成整个样本空间。在此基础上，利用EFAST法计算每个参数的一阶敏感性指标(主效应)，及包含了与其他参数交互效应的高阶总敏感性指标(总效应)。以同一输出指标为分组，作出各个影响因素变异度最小状况下的敏感性指标图，如图6所示。

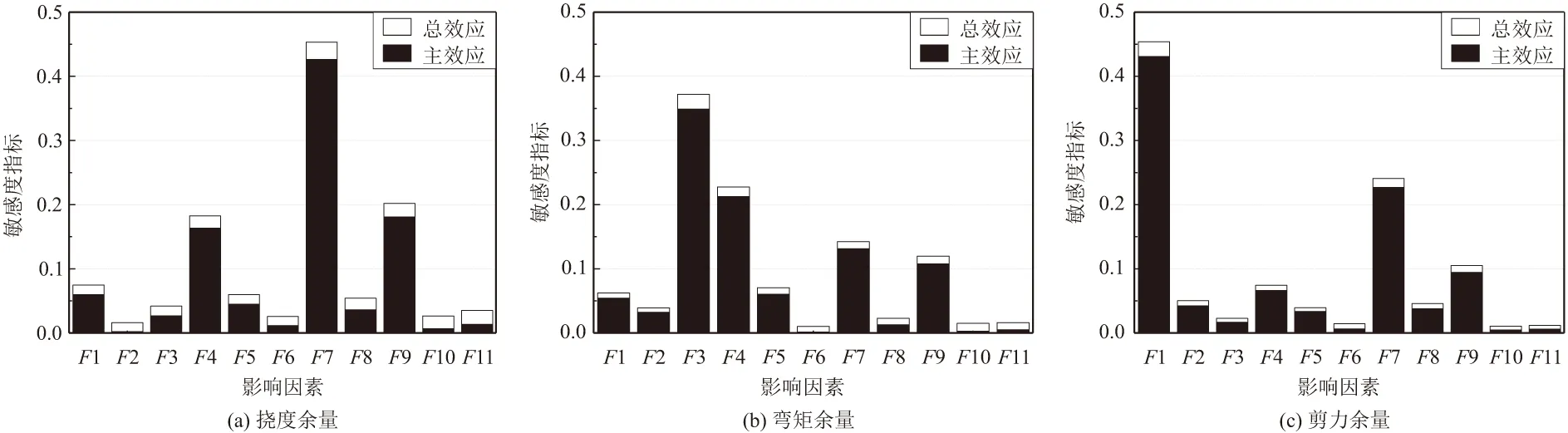
图6 影响因素COV最小时各评价指标敏感度

图6中，黑色表示主效应值，白色对应总效应值。由于总效应值包含了单因素的主效应值及因素间的交互作用引起的效应值，故总效应恒不小于主效应。且由图6可见，对于本文中的预应力空心板连续梁桥而言，本次敏感性分析中选择的影响因素间的交互作用对于所有影响因素的敏感性排序无突出影响。

由图6a，对于挠度余量，将影响因素按总效应值由大至小排序则有：F7>F9>F4>F1>F5>F8>F3>F11>F10>F6>F2。其中效应值数倍高于其他因素的影响因素有：构件密度F7、车道荷载F9、预应力筋强度F4，其主效应值分别为0.426，0.181，0.164，总效应值分别为0.453，0.202，0.183；由式(3)可知，效应值反映的是该因素对方差的贡献在所有因素贡献总和中的占比，故F7，F9，F4对挠度余量具有显著影响；其余因素总效应共占比约33%，其中混凝土强度F1占比7%，预应力筋面积F5占6%，桥面铺装重度F8占5.4%，Ⅱ级钢筋强度F3占比约4%，其影响也不可忽略；剩余4个因素则总效应共占比约10%，影响极小。

同理，对于弯矩余量，按影响因素总效应值由大至小进行排序有：F3>F4>F7>F9>F5>F1>F2>F8>F11>F10>F6，其中具有显著影响的因素为Ⅱ级钢强度F3、预应力筋强度F4、构件密度F7、车道荷载F9，其总效应值分别为0.372，0.228，0.142，0.120；另有较大影响的因素为预应力筋面积F5和混凝土强度F1。对于剪力余量，按影响因素总效应值由大至小进行排序有：F1>F7>F9>F4>F2>F5>F8>F3>F10>F11>F6，其中具有显著影响的因素为混凝土强度F1、构件密度F7 及车道荷载F9，相应的总效应值分别为0.464，0.237，0.100。有较大影响的因素有为预应力筋强度F4、Ⅰ级钢强度F2、预应力筋面积F5。

对比三个不同评价指标则可发现，构件密度F7和车道荷载F9对三个输出指标均存在显著影响；而支座弹性模量F6、冲击系数F10、均匀温度荷载F11则在各个排序中均位于末尾，即对三个输出指标均不敏感。且针对不同的评价指标影响因素的敏感性差异显著。

为探究影响因素的不同离散程度对于因素的敏感性是否存在影响，以挠度余量指标为例，将三个变异度下的影响因素总效应值列入表3。

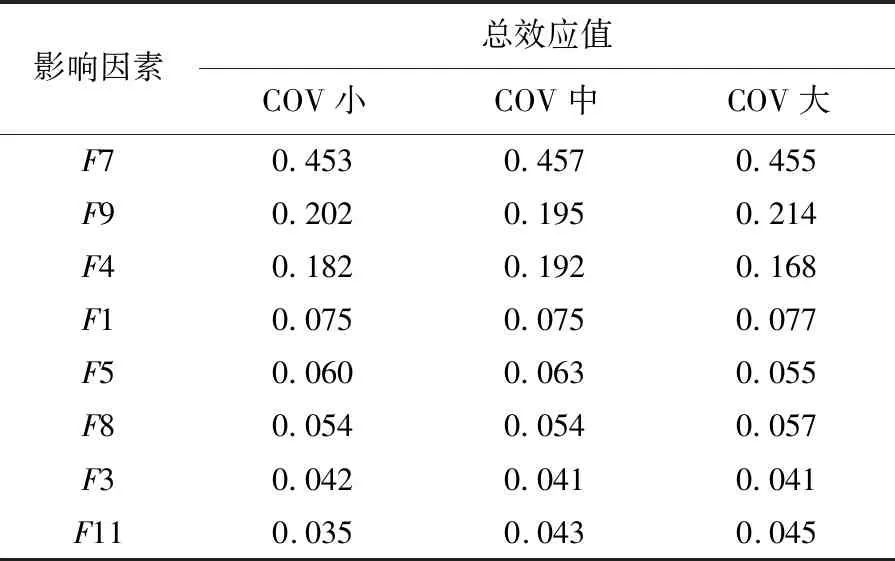
表3 挠度余量重要影响因素不同COV下的总效应

表3中列出11个影响因素中排序前8即较为重要的8个影响因素的总效应值。由表3中数据可见，除F11以外的各因素在COV逐步变大的情况下并没有表现出任何单调性；同时各个COV下的效应值差距不大。由此，本文设定的COV变化程度下，影响因素的离散程度对其敏感性程度并无明显作用。也从侧面说明了EFAST算法具有良好的稳定性。

4 结 论

本文以武汉某高速公路桥为例，建立预应力空心板连续梁桥有限元模型并进行不确定性计算，在此基础上结合LSSVM模型，采用EFAST算法进行敏感性分析，针对本例得到以下结论：

(1)构件密度F7和车道荷载F9对于桥梁挠度余量、空心板弯矩余量及剪力余量均存在显著影响，敏感程度高；而支座弹性模量F6、冲击系数F10、均匀温度荷载F11则对三个评价指标均得到远小于0.1的敏感度指标值，即影响较小，可忽略。

(2)对于不同评价指标，影响因素的敏感程度存在明显差异。对于挠度余量，敏感性由大至小为构件密度F7、车道荷载F9及预应力筋强度F4影响显著；对于弯矩余量，敏感性由大至小有为Ⅱ级钢强度F3、预应力筋强度F4、构件密度F7及车道荷载F9影响显著；对于剪力余量，敏感性由大至小有为混凝土强度F1、构件密度F7及车道荷载F9影响显著。

(3)由本文设定的三种影响因素离散程度可见，因素离散程度的变化不一定能影响其敏感性程度。