板底脱空对无砟轨道结构模态的影响
2020-11-07郭杰毕澜潇徐天赐赵坪锐
郭杰 毕澜潇 徐天赐 赵坪锐
(西南交通大学高速铁路线路工程教育部重点实验室,成都 610031)
作为无砟轨道的一种典型病害,脱空对轨道结构的性能有较大影响,其产生的原因较为复杂,如设计、施工、材料性能、服役环境等。脱空时轨道板的承力与传力特性发生变化,进而影响轨道结构的振动形态。文献[1-4]分析了无砟轨道脱空对轨道结构和车辆系统的静力、动力性能的影响,文献[5-6]分析了材料参数或某一种脱空形式对轨道结构模态的影响。
本文以CRTS Ⅲ型板式无砟轨道为对象,先对脱空厚度合理的处理方法展开研究,再分析不同脱空形式对轨道结构模态的影响。
1 有限元模型及计算参数
将轨道结构视为无阻尼系统。主要计算参数:轨道板长5.6 m,宽2.5 m,厚0.21 m;自密实混凝土厚0.1 m;底座板宽3.1 m,厚0.3 m;轨道板弹性模量为36 GPa,自密实混凝土和底座板弹性模量均为34 GPa;路基面支承刚度取76 MPa/m,扣件刚度取50 kN/mm。模型中,钢轨视为点支承连续梁,采用梁单元模拟;扣件忽略其阻尼和纵横向阻力,采用线性弹簧单元模拟;轨道板、自密实混凝土和底座板均采用实体单元模拟。路基采用线性弹簧单元模拟,其刚度的计算见文献[7]。轨道结构各层间采用接触单元,模型长度取3 块轨道板,CRTS Ⅲ型板式无砟轨道有限元模型见图1。
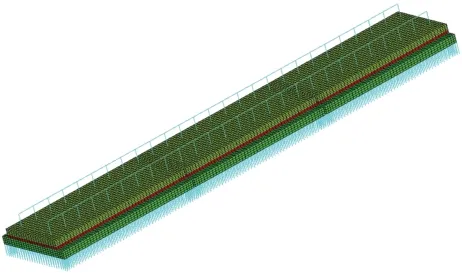
图1 CRTS Ⅲ型板式无砟轨道有限元模型
模型的边界条件:约束钢轨节点的全部位移;约束轨道结构端部的纵横向位移;约束地基弹簧底部的全部位移。
轨道板脱空形式如图2 所示。其中l和w分别为脱空的长度和宽度。板边脱空假定沿轨道板纵向完全脱空,以w表征脱空尺寸。板端脱空假定沿轨道板横向完全脱空,以l表征脱空尺寸。板角和板中脱空以l×w表征脱空大小。分析工况取图2 中的1 种或2种脱空形式的组合。

图2 轨道板脱空示意
为叙述方便,将3 块轨道板从左至右依次命名为1,2,3 号轨道板。计算轨道结构的前10 阶模态,采用分块兰索斯法[8]提取模态。因计算工况较多,分析振型时仅列出振型发生较大变化的工况。由于底座板和自密实混凝土接触良好,其振型同步,故振型图仅包含轨道板和自密实混凝土。脱空主要影响高阶模态[5],故本文重点分析第10节模态。
2 计算结果与分析
2.1 脱空厚度处理方法
本文脱空厚度取3 mm,先论证其合理性。以板端脱空为例,脱空长度取0.4 m,分别计算无脱空、脱空厚度3 mm 和脱空厚度方向完全脱空时轨道结构的模态。轨道结构第2阶振型见图3。

图3 轨道结构第2阶振型(单位:mm)
由图3 可知:板端脱空长0.4 m 时,脱空厚度取3 mm 和厚度方向完全脱空时轨道结构固有频率相差不大,但轨道结构第2 阶振型有所不同。脱空厚度为3 mm 时波峰位于2 号轨道板,厚度方向完全脱空时波峰位于3 号轨道板,而板端脱空长度为0.4 m 时脱空对轨道结构第2 阶振型影响较小[5],故研究脱空状态下轨道结构模态变化规律时,厚度方向不宜采用完全脱空,而应取一定的脱空厚度,具体取值应通过现场调研确定。
2.2 脱空位置对轨道结构模态的影响
2.2.1 板边脱空及其组合
板边脱空组合取2 号轨道板上下两边对称脱空。板边脱空时,脱空宽度依次取0.4,0.8,1.2,1.6 m;板边脱空组合时,两边脱空宽度依次取0.4,0.6,0.8,1.0 m。轨道结构固有频率随振动阶数变化曲线见图4。可知:①板边脱空与其组合固有频率变化趋势基本一致,均随振动阶数的增大而增大;②无脱空、板边脱空宽度为0.4,0.8,1.2 m 及板边脱空组合时,第1阶到第2阶、第6阶到第7阶和第9阶到第10阶固有频率增大明显,而板边脱空宽度为1.6 m 时,仅在第1 阶到第2阶和第6阶到第7阶固有频率增大明显;③脱空宽度对第10 阶固有频率影响最大,板边脱空宽度为1.6 m 和板边脱空组合脱空宽度为1.0 m 时固有频率较无脱空分别降低19.6%和10.6%。

图4 轨道结构固有频率随振动阶数变化曲线
板边脱空时轨道结构第10阶振型见图5。
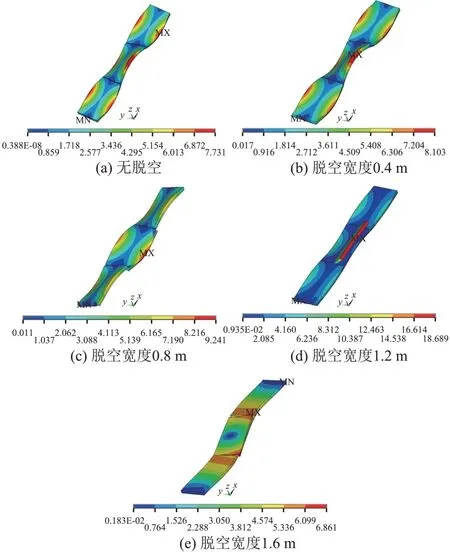
图5 板边脱空时轨道结构第10阶振型(单位:mm)
由图 5 可知:①脱空宽度为 0.4 m 和 0.8 m 时,轨道板和自密实混凝土的振型与无脱空时相似,均为空间扭转,但波峰由6 个减少为2 个,位于2 号轨道板长边中部;②脱空宽度为0.8 m 时,脱空区域板角处轨道板和自密实混凝土的振动方向相反,两者间会产生一定的拍打作用,对轨道结构有一定的破坏作用;③脱空宽度为1.2 m 时,脱空区域轨道板剧烈垂向振动,轨道板与自密实混凝土分离明显,振动跟随性显著下降,轨道板和自密实混凝土间的拍打作用较脱空宽度为0.8 m 时强烈;④脱空宽度为1.6 m 时,振型与无脱空时第9阶振型相似,均为空间扭转,为横向、纵向、垂向振动的叠加,且以横向振动为主。
脱空宽度为1.6 m 时,第8,9 阶振型与脱空宽度为1.2 m 时第10 阶振型类似,均表现为脱空区域轨道板剧烈垂向振动。
2.2.2 板角脱空及其组合
本文取板角脱空的长宽比与轨道板长宽比相等,依次取板角脱空尺寸(长×宽)为0.896 m×0.4 m,1.344 m×0.6 m,1.792 m×0.8 m,2.240 m×1.0 m。板角脱空组合为两个对角方向的板角脱空,2 个板角脱空尺寸相同,均与仅有1 个板角脱空时相同。板角脱空时轨道结构第10阶振型见图6。
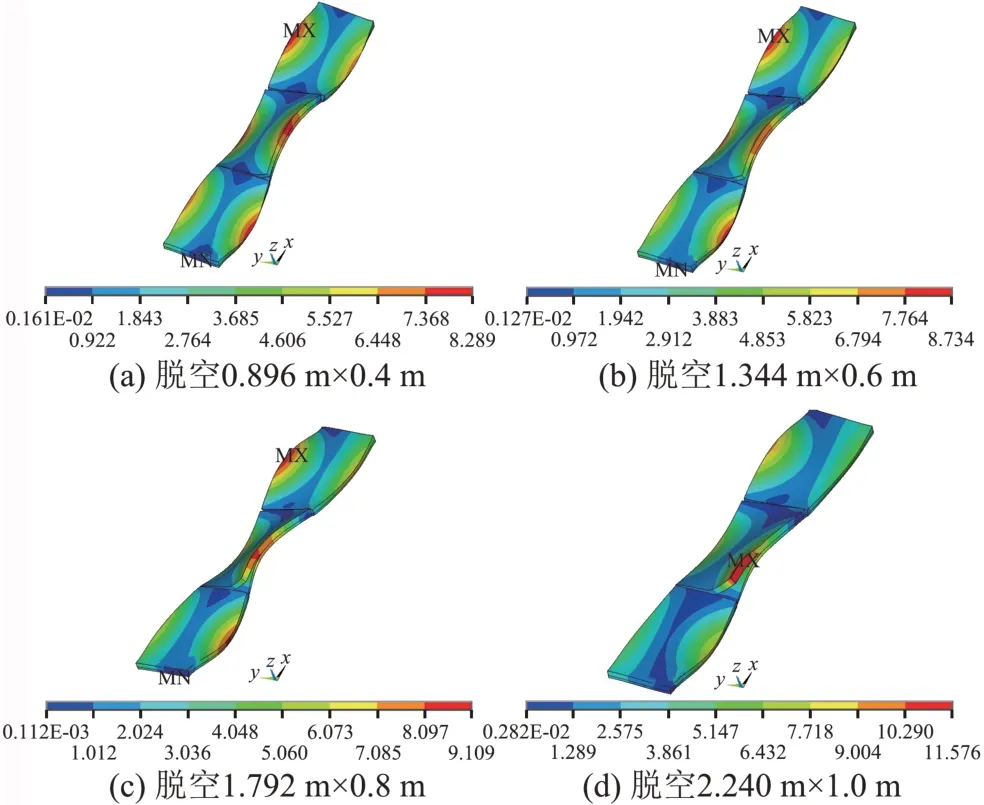
图6 板角脱空时轨道结构第10阶振型(单位:mm)
由图6 可知:①板角脱空时轨道板和自密实混凝土的第10阶振型与无脱空时相似,均为以垂向振动为主的空间扭转;②随脱空尺寸增大,波峰由6个逐渐减至1 个,且波峰由轨道板长边中部逐渐移至2 号轨道板的板角脱空区;③与无脱空时相比,当板角脱空尺寸为2.24 m×1.0 m 时,在板角处轨道板与自密实混凝土分离较明显,振动跟随性明显降低,轨道板将对自密实混凝土产生较大的拍打作用,造成轨道结构损伤。而板角脱空组合时第10 阶振型脱空区域轨道板板角将交替对自密实混凝土产生拍打作用。
2.2.3 板端脱空及其组合
板端脱空组合为2 号轨道板两端对称脱空,且两端脱空尺寸均与仅一端脱空时相同。依次取脱空长度为0.4,0.8,1.2,1.6 m。轨道结构固有频率随振动阶数变化曲线见图7。可知:①板端脱空及其组合固有频率变化趋势基本一致,均随振动阶数的增大而增大;②无脱空和脱空长度为0.4,0.8,1.2 m时,第1阶到第2阶、第6阶到第7阶和第9阶到第10阶固有频率增大明显,而脱空长度为1.6 m 时,仅在第1 阶到第2 阶和第6 阶到第7 阶固有频率增大明显;③随脱空长度增大固有频率呈减小趋势,其中第10 阶减幅最大,与无脱空时相比板端脱空及其组合固有频率分别减小18.4%和23.5%。

图7 轨道结构固有频率随振动阶数变化曲线
板端脱空时轨道结构第10阶振型见图8。

图8 板端脱空时轨道结构第10阶振型(单位:mm)
由图8 可知:①板端脱空长度为0.4,0.8 m 时,轨道板和自密实混凝土的第10阶振型与无脱空时相似,均为空间扭转;②脱空长度为0.8 m 时,脱空区域轨道板板角和自密实混凝土振动方向相反,两者将发生较大的拍打作用,可导致板角处轨道结构损伤;③脱空长度为1.2 m 时,脱空区域轨道板表现为极为剧烈的垂向振动,脱空区域轨道板与自密实混凝土分离极为明显,轨道板将对自密实混凝土产生剧烈的拍打作用,导致轨道结构严重损伤,而在非脱空区域振型基本无变化;④脱空长度为1.6 m 时,振型与无脱空时第9阶振型相似。
脱空长度为1.6 m 时第8阶、第9阶振型与脱空长度为1.2 m 时第10 阶振型类似,均表现为脱空区域轨道板剧烈垂向振动。
板端脱空组合时轨道结构第10阶振型见图9。
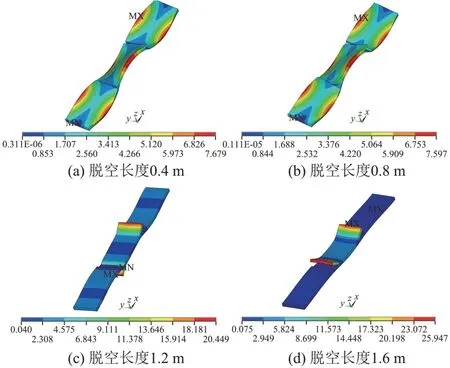
图9 板端脱空组合时轨道结构第10阶振型(单位:mm)
由图9可知:①板端脱空组合情况下,脱空长度为0.4,0.8 m 时,轨道板和自密实混凝土的第10 阶振型与无脱空时相同,均为空间扭转。②板端脱空长度为1.2,1.6 m 时,脱空区域轨道板剧烈垂向振动,脱空区域轨道板与自密实混凝土分离极为明显。脱空长度为1.2 m 时,轨道板两端交替对自密实混凝土产生剧烈拍打作用,造成脱空区域轨道结构严重损伤;脱空长度为1.6 m 时,2 个板端同时出现波峰,板端轨道板与自密实混凝土分离极为明显,轨道板两端将同时对自密实混凝土产生剧烈的拍打作用,造成脱空区域轨道结构严重损伤,而在非脱空区域振型基本无变化。
脱空长度为1.6 m 时,第7阶振型与第10阶类似,表现为脱空区域轨道板剧烈垂向振动,轨道板两端同时对自密实混凝土产生剧烈的拍打作用;第9 阶振型与脱空长度为1.2 m 时第10 阶振型类似,表现为脱空区域轨道板剧烈垂向振动,轨道板两端交替对自密实混凝土产生剧烈的拍打作用。
2.2.4 板中脱空及其与其他脱空形式的组合
只分析板中脱空对轨道结构模态的影响时,板中脱空尺寸同板角脱空,由计算结果可知其对轨道结构模态影响很小,本文不再赘述。
脱空组合考虑2 种脱空形式,将板中脱空分别与板角脱空和板端脱空组合。不同脱空形式组合时,板中脱空尺寸不变,均取0.896 m×0.4 m,改变其他形式脱空的尺寸以表征不同脱空程度。板角脱空尺寸和板端脱空尺寸分别与2.2.2 节和2.2.3 节相同。轨道结构固有频率随振动阶数变化曲线见图10。
由图10(b)和图10(c)可知:板中脱空与板角脱空组合对固有频率的影响与仅有板角脱空时相差不大,即板中脱空与板角脱空组合对固有频率的影响由板角脱空决定。
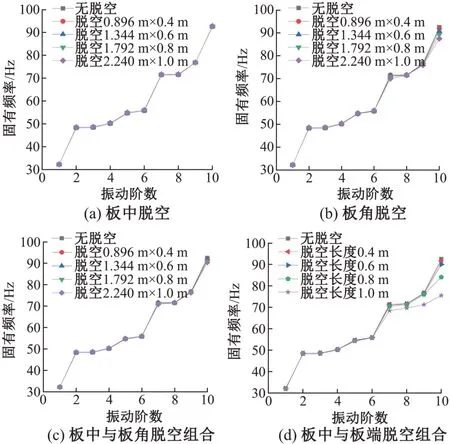
图10 轨道结构固有频率随振动阶数变化曲线
对比7(a)与图10(d)可知:板中脱空与板端脱空组合对固有频率的影响与仅有板端脱空时相差不大,即板中脱空与板端脱空组合对固有频率的影响由板端脱空决定。
由以上分析可知,板端脱空组合对轨道结构固有频率和振型影响最大,而板中脱空影响最小。
2.3 脱空形状对轨道结构模态的影响
取板中脱空面积为2.24 m2,脱空形状分别为长方形、正方形和圆形。长方形长2.24 m、宽1.0 m;正方形边长1.497 m;圆半径为0.844 m。3 种脱空形状轨道结构固有频率随振动阶数变化趋势几乎相同,且与无脱空时基本无差异,即很难通过模态识别板中脱空的形状。
2.4 轨道板自振应力分布
自振应力可表征结构的振动强度,自振应力越大,表明该处的振动越剧烈。无脱空时轨道板自振应力在扣件支点处最大,这是因为轨道板大多数阶数的振动以垂向振动为主,在扣件的约束作用下自振应力集中于此,故研究高速铁路无砟轨道结构减振降噪时,应将扣件支点处作为重点之一。
不同脱空状态时轨道板第10阶自振应力见图11。可知,板边脱空宽1.2 m 时轨道板第10 阶自振应力在脱空区域轨道板与自密实混凝土接触边缘最大,其余3种工况轨道板第10阶自振应力在脱空区域与自密实混凝土接触边缘较大,表明接触边缘轨道板受力不利,为轨道板的薄弱区域。最大自振应力出现在2 号轨道板端部扣件支点处,因受扣件约束所致。

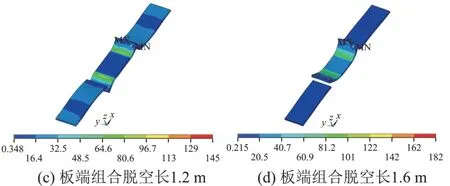
图11 不同脱空状态时轨道板第10阶自振应力(单位:MPa)
3 结论
本文研究了不同脱空状态对无砟轨道模态的影响,并对轨道板的自振应力进行了分析。结论如下:
1)分析脱空对轨道结构模态的影响时,脱空厚度方向不宜作完全损坏处理,而应取一定的脱空厚度,具体取值可通过现场调研情况确定。
2)板端脱空组合对轨道结构模态的影响最大,板中脱空最小,其余脱空状态影响各不相同,但均对高阶模态影响较大。
3)板中脱空时,脱空形状对轨道结构模态几乎没有影响。
4)无脱空时轨道板的自振应力在扣件处最大。研究高速铁路无砟轨道结构减振降噪时,应将扣件支点作为重点之一。
5)不同脱空状态下轨道板自振应力在脱空区域与自密实混凝土接触边缘较大,该处为轨道板的薄弱区域。
