解析几何中绚丽的一幕

邹海斌

[摘  要] 文章从圆中两个性质类比到椭圆中的两个重要结论开始，探究了椭圆中美好的定值问题，以-■为抓手，证明了一些美妙的结论，在解析几何里一些图形中两条动直线斜率乘积为定值-■;同时又说明了定值并非都是-■，可以是与a和b有关的其他值;最后研究了已知两直线斜率乘积为-■的椭圆中的定值问题.

[关键词] 类比;特殊到一般;方程思想;定值问题

代数和几何是数学的两个重要的组成部分，那么解析几何的出现实现了代数和几何的融合，形成了形和数的统一.通过建立坐标系，曲线就可以用一个代数方程来描述，解析几何的本质就是用代数的方法来研究各类曲线的性质. 椭圆是圆锥曲线中不可或缺的一员，具有很好的研究价值.比如在天文学上，我们知道行星绕太阳运行的轨迹就是椭圆，太阳刚好处在椭圆的一个焦点上;在生活中，电影放映机的聚光灯泡的反射面就是椭圆面，灯丝在一个焦点上，影片门在另一个焦点上. 在高考中，椭圆也扮演着非常重要的角色，因为它可以很好地考查学生的综合能力，特别是计算能力和问题的转化能力，椭圆是非常好的一个考查对象，所以研究椭圆曲线的性质是非常有意义的.

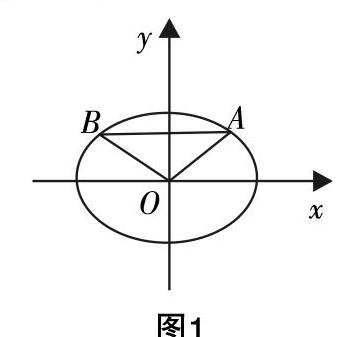
我们知道在某种意义上可以把椭圆看成是圆的延伸，所以很多椭圆的性质可以从圆中类比过来，比如在圆O中，AB为直径，P为圆上异于A，B的一点，我们有kAPkBP=-1.

那么在椭圆中，我们有性质（1）：对于椭圆■+■=1，A，B为椭圆上关于原点对称的两点，P为椭圆上异于A，B的一点，我们有kAPkBP=-■.

又比如在圆O中，AB为不过原点的弦，P为弦AB的中点，有kOPkAB=-1，这就是圆中的垂径定理.

那么在椭圆中，我们有性质（2）：对于椭圆■+■=1，AB为椭圆中不过原点O的一条弦，P为弦AB的中点，我们有kOPkAB=-■.

这两个性质是椭圆中的两个重要结论，两条动直线斜率乘积为定值-■，同时也揭开了探究椭圆中美好性质的序幕，特别是还有哪些动直线斜率乘积也为定值，定值是多少？这引发了我们探究的兴趣. 当然定值问题只是椭圆美好性质中的一部分，不过是非常绚丽的一部分.在变化中寻求不变量一直是我们数学研究的一个重要方向，而动中找定又是一个非常重要的数学思想方法，下面我们就来探究一下，椭圆中还有哪些美妙的定值.

定值问题，变化中不变的东西，我们怎么探究呢？从哪里入手呢？我们不可能每次上来就知道哪些东西是定值，哪两条直线斜率乘积会是定值，那么从特殊到一般的思想方法就起到了尤为关键的作用，当然你首先要有一双善于发现的眼睛.我们来看下面一个例子.

在平面直角坐标系xOy中，已知椭圆■+■=1，A，B为椭圆上两点，△AOB的面积为■，射线OA，OB的斜率分别为k1和k2，求k1k2的值.

解：求k1k2的值，采用比较多的角度是用点去求k关系，我们下面就采用这个方法.

设A（x1，y1），B（x2，y2），则OA方程：y=■x，点B到直线OA的距离d=■，S△AOB=■■■=■，我们有x2y1-x1y2=2■. 两边平方得到x■y■+x■y■-2x1x2y1y2=8，即2x■y■+2x■y■-4x1x2y1y2=16，而k1k2=■，接下去如何化简才能得到我们想要的呢？我们知道，设点必然要用到曲线方程，这里是椭圆方程，我们就有x■+2y■=4，x■+2y■=4，接下去关键的一步是把上面的16寫成4×4，消常数项，使等式两边变成齐次式，代入可得到2x■y■+2x■y■-4x■x■y■y■=x■x■+2x■y■+2x■y■+4y■y■，化简可得（x1x2+2y1y2）2=0，所以k1k2=■=-■.

从这个k1k2的值为-■这个结果来看，我们敏感地发现这个值就是-■，那么这时候我们会想，上面这个题目有没有一个一般性的结论，能不能从这样一个特殊的情况推广到一般情况？这里的关键是“△AOB面积为■”有没有特别的含义，经过分析发现■=■ab，所以我们猜想得到下面的结论.

结论1：在平面直角坐标系xOy中，已知椭圆■+■=1，A，B为椭圆上两点，△AOB的面积为■ab，射线OA，OB的斜率分别为k1和k2，求证：k1k2=-■.

证明：同样设A（x1，y1），B（x2，y2），则OA方程：y=■x，点B到直线OA的距离d=■，S△AOB=■■·■=■ab，我们有x2y1-x1y2=ab. 两边平方得到x■y■+x■y■-2x■x■y■y■=a2b2，接下去处理有点不一样，我们把等式变形成■（x■y■+x■y■-2x■x■y■y■）=1，把右边的1看成1x1. 又因为■+■=1，■+■=1，代入得到■（x■y■+x■y■-2x■x■y■y■）=■+■+■+■，化简可得■+■+■=0，即■+■■=0，所以k■k■=■=-■，证毕. 我们把结论1证明好了，是个漂亮的结果，我们感到很高兴，那么我们是不是就此结束了呢？答案是否定的，我们要进一步研究，因为对于-■这个定值特别有感触，我们想是不是还有哪些直线斜率乘积也是定值-■呢？经过研究，运用特殊到一般的数学思想方法，我们还发现了下面几个漂亮的结论.

结论2：在平面直角坐标系xOy中，椭圆方程■+■=1，直线l不与x轴垂直，与椭圆相切，直线l与圆x2+y2=a2+b2交于A，B两点，设直线OA，OB的斜率分别为k■和k■，求证：k■k■=-■.

结论3：在平面直角坐标系xOy中，椭圆方程■+■=1，A为右准线上任意一点，F■，F■为椭圆的左、右焦点，过F■作直线AF■的垂线BF■交椭圆于B，设直线AB和OB的斜率为k■和k■，求证：k■k■= -■.

结论4：在平面直角坐标系xOy中，椭圆方程■+■=1，M（x■，y■）为椭圆上一点，从原点O向圆M：（x-x■）2+（y-y■）2=■作两条切线，与椭圆交于A和B两点，直线OA，OB的斜率分别为k■和k■，求证：k■k■=-■.

结论5：在平面直角坐标系xOy中，已知椭圆C方程■+■=1，椭圆D方程■+■=1，过椭圆D 上一点P作椭圆C的两条切线，切点分别为A和B，直线PA，PB的斜率分别为k■和k■，求证：k■k■=-■.

下面我们先来证明结论2：设A（x1，y1），B（x2，y2），因为直线l不与x轴垂直，所以斜率存在. 设直线l方程为y=kx+m，与椭圆方程■+■=1联立得到（b2+a2k2）x2+2kma2x+m2a2-a2b2=0. 因为直线l与椭圆相切，所以Δ=0，化简可得m2=b2+a2k2. 直线l与圆x2+y2=a2+b2联立可得（1+k2）x2+2kmx+m2-a2-b2=0，由韦达定理知x■+x■=■，x1x2=■. 所以y1y2=（kx1+m）（kx2+m）=k2x1x2+km（x1+x2）+m2=■，

所以k1k■=■=■，把m2=b2+a2k2代入，则k1k2=■=-■，证毕.

结论3的证明思路和上面一样，用点去证k关系，把要证的斜率k的关系转化为坐标关系，简单证明如下：

设A■，y1，B（x2，y2），F2（c，0），

则k1k2=■·■=■.

因为k■k■=■·■=-1，即y■y■= -■（x2-c）.

又因为点B在椭圆上，所以有y■=b21-■，

所以k■k■=■=-■为定值.

对于结论4，我们的证明方法和上面的不一样，如果我们从点的角度，把斜率k的关系转化为点坐标关系是不好证明的，那么怎么去证明呢？这里我们主要运用方程的思想去证明. 证明如下：

设OA方程：y=k■x，OB方程：y=k■x，因为OA与OB为圆M的切线，那么我们不妨设过原点O的圆M的切线方程为y=kx，则圆心M到切线的距离d=■=■=r，两边平方整理得到（x■-r2）k2-2x0y0k+y■-r2=0. 因为k■和k■为方程（x■-r2）k2-2x■y■k+y■-r2=0的两根，所以k1k2=■. 因为M在椭圆上，有y■=b21-■，代入得到k1k2=■=■=■=-■，证毕.

同样的，我们也可以用方程的思想来证结论5，证明如下：

设P（x0，y0），为了计算上的方便，这里我们运用了整体思想，设过点P的椭圆C的切线l方程为y=kx+t，其中t=y0-kx0. 直线l与椭圆C：■+■=1联立得到（b2+a2k2）x2+2ka2tx+a2t2-a2b2=0. 因为l与椭圆C相切，所以Δ=0，化简可得t2=b2+a2k2，把t=y0-kx0代入得到（x■-a2）k2-2x0y0k+y■-b2=0. 因为直线AP和BP都为椭圆C的切线，斜率分别为k■和k■，所以k■和k■为方程（x■-a2）k2-2x0y0k+y■-b2=0的两根，所以k1k2=■. 又因为点P在椭圆D上，有y■=2b21-■，则k1k2=■=■=■=-■，证毕.

这样我们就完成了结论2、3、4、5的证明，那么除了直线斜率乘积为定值 -■之外，有没有其他的直线斜率乘积是定值了呢？经过研究发现，答案是肯定的，比如下面的一个例子.

在直角坐标系xOy中，已知椭圆■+■=1的右顶点和上顶点分别为A和B，四边形ABCD内接于椭圆，AB∥DC，记AD，BC的斜率分别为k■，k■，求证：k■k■为定值.

證明：设C（x1，y1），D（x2，y2），直线AB斜率为-■，设直线CD方程：y=-■（x-x1）+y1，与椭圆■+■=1联立得到2b2x2-（2b2x1+2aby1）x+b2x■+2abx1y1+a2y■-a2b2= 0.因为点C在椭圆上，有y■=b21-■，代入得到2b2x2-（2b2x1+2aby1）x+2abx1y1=0，由韦达定理知，x1x2=■=■，所以x2=■y1，代入直线CD方程得y2=■x1.所以k1k2=■·■=■·■= ■为定值，证毕.

在我们的研究中，我们还发现了一个有意思的事情，就是把“两直线斜率乘积为定值-■”作为条件，也可以得到椭圆的一些美好的结论，这类问题可以看成是斜率关系的逆问题，也非常值得研究，比如下面的例子.

在直角坐标系xOy中，已知椭圆方程■+■=1，A，B为椭圆上的两点，直线OA与直线OB的斜率乘积为-■，点B关于x轴的对称点为C点，

求证：（1）OA2+OB2为定值;

（2）直线AC的斜率为定值.

证明（1）：设A（x1，y1），B（x2，y2），C（x2，-y2），OA方程：y=k1x，与椭圆■+■=1联立得到x■=■，同理设OB方程：y=k2x，可得到x■=■.

因为k1k2=-■，即k■=■，则x■=■=■，所以x■+x■= ■+■=■=a2，y■+y■=k■x■+k■x■=k■■+k■■=■=b2，所以OA2+OB2=x■+y■+x■+y■=a2+b2为定值.

直线AC的斜率kAC=■，接下去怎么处理呢？这里我们用一个小技巧，两边平方，得到kAC2=■■=■，由（1）知x■+x■=a2，y■+y■=b2，则k■=■. 又因为k1k2=■= -■，所以k■=■=■=■为定值，所以直线AC的斜率为定值.

以上是对椭圆中直线斜率关系问题的探究，我们得到了椭圆中的一些美好的性质，当然这仅仅是冰山一角，但足以体现椭圆的美. 这种美是圆锥曲线，也是整个解析几何中非常绚丽的一幕，这些性质有的还可以类比到双曲线中，这里就不做研究了.

结束语

我们教师在平时的教学中，自身要多归纳，多总结，教学相长，不断提升自己，俗话说打铁还需自身硬，要有一双发现问题的眼睛，有探索的精神，有解决问题的能力，这样才能做到会当凌绝顶，一览众山小. 基于数学核心素养下的解题教学，是每位教师终生探究的课题，望共勉之.