数学实验:潜行“学为中心”课堂的有效方式
2020-11-06张小曼
张小曼
摘 要:数学实验是潜行“学为中心”课堂的有效方式。文章基于“学位中心”教学理论探究了小学数学实验教学中学生介入数学实验和学生沉浸数学实验的实施过程。认为小学数学实验教学中,教师应放手让学生去操作,全面解放学生,引导学生在操作过程中学习数学,并进行有意义的建构,使数学课堂真正回归“学为中心”。
关键词:小学数学;数学实验;学为中心
“学为中心”的课堂理念得到了广大教者的普遍认同,并基于这一理念展开了系列化研究,形成“学科核心素养”为中心目标、“數学学习活动”为中心内容、“激活学生主体性”为中心方法等“学为中心”的研究成果 [1]。综合分析“学为中心”教学理论探索和教学实践,数学实验是潜行“学为中心”课堂的有效方式,它引导小学生凭借物质、仪器、学具和技术手段等,坚持以数学理论和科学的教学理论为指导,放手让学生去操作,全面解放学生,学生在操作过程中学习数学,并进行有意义的建构,使数学课堂真正回归“学为中心”。
一、学生介入数学实验设计过程
有效的数学实验离不开系统性设计,然而传统数学课堂模式下,数学实验设计的任务主要由教师实施,学生主体性没有得到充分的尊重。“学为中心”课堂模式下,数学实验设计要打破教师“霸权话语”模式,引导学生介入到数学实验设计过程,让学生在介入过程中,明确实验的目的、实验操作程序和实验材料等,从而扩大数学实验效应,让数学课堂回归“学为中心”。
1. 发问:让数学实验有的放矢
小学数学实验设计首先要解决“为什么实验”的问题,这就需要教师在引导学生介入数学实验时,能够培养学生“发问”的意识,让学生学会提问,从而为数学实验的开展创造可能,让学生的数学实验做到有的放矢,并发挥问题驱动效应,让学生在实验中发现问题,在问题引领下进行有目的的实验。
例如,“圆的认识”,笔者先让学生利用圆规画出一个圆,再让学生仔细观察圆,说出圆心、半径和直径等各个组成部分,最后根据自己的实验操作,围绕圆的基本组成部分,提出一些问题。很快,学生做出了积极的响应,“圆的半径是不是都是相等的?”“半径和直径之间的关系是什么?”“圆的面积大小跟什么有关系?”“圆的周长大小跟什么有关系?”……
这个环节,利用学生先行实验,让学生提出问题,这些问题有效地释放了学生好奇心,让学生提出形形色色的问题,激发学生数学实验的内驱力,学生在好奇心驱动下将积极地开展实验。
发问环节,教师要加强引导,发挥主导作用。面对学生提出的问题,教师既要保护学生提问的自信心,又要使问题指向课堂教学目标。对于价值密度较低的问题,教师可以发挥学生同伴的学习优势,让学生通过简单的问答解决;此外,通过合理地对问题进行取舍,提炼出有价值的问题,能够引导学生透过现象深入本质,深化学生对“圆”的了解和认识。
2. 假设:让数学实验期待满满
尽管数学实验和科学实验存在较大的差异,但是数学作为一门自然学科,它们在思想上具有相同之处。因此,数学实验设计时,我们要善于利用科学实验的思路,对学生进行有效的引领,让学生积极主动地参与到数学实验设计中,其中一种可行的思路就是引导学生在动手实验之前进行假设 [2]。通过假设,不仅能够使数学实验的目的性得到进一步的增强,而且能够有效地激发学生数学实验期待感,让学生以饱满的情绪投入到数学实验中。
“圆的认识”在学生提出各自的问题后,我们可以围绕提炼的高价值密度的问题,引导学生对问题进行假设。如“圆的面积大小跟什么有关系”这个问题,我们不妨让学生做出自己的假设,学生提出的假设主要包括两种观念:跟直径或者半径有关系。
由于学生围绕提出的问题进行了假设,这样学生在实验的过程中就具有明确的方向,去围绕半径或者直径和面积的关系进行探究。这就造成探究目的的唯一性,但是探究的方法没有规定性,从而为学生设计数学实验提供了多元化的思维空间,学生根据假设设计出多样化实验,最终实现殊途同归。
学生提出假设时,教师要进行合理的引导。学生提出的假设要建立在学生既有生活、知识、经验等基础上。因此,在学生提出假设时,教师不妨让学生说一说自己提出这种假设的依据,从而使学生既有的生活、知识和经验等得到有效的整合,突出学生中心,提高学生假设的科学性、合理性,避免课堂学习时间的无谓消耗。
3. 预案:让数学实验循序渐进
数学实验,无论规模大小,都是一项严谨的学习活动。如何保障学习活动的有效性,让数学实验更加切合“学为中心”,这是数学实验设计需要解决的重点问题之一。因此,数学教师要引导学生自主设计预案,针对数学实验目的,即学生提出的问题,做出的假设等,提出数学实验设计方案。数学实验方案的设计不仅要注重规范性,包括数学实验的名称、实验目的、实验材料、实验过程、实验记录和实验结果等,而且还要突出学生主体性,让学生去设计,针对不同学段的学生,教师可以给予合适的引导。例如,教师可以向学生提供一份数学实验方案,让学生透过自主性观察,了解数学实验方案的基本结构,避免教师抛给式的呈现方式,以突出“学为中心”。
预案设计过程中,一个重要环节是数学实验材料的准备,目前数学实验材料主要由教师提供,或者利用教材提供的配套实验材料。这种材料供给方式不能突出“学为中心”,需要教师给予学生自主收集、准备材料的机会。如在学生提出“圆的面积大小跟直径或半径有关系”这一假设后,让学生设计实验方案,根据实验方案中所需要的实验材料,让学生就地取材。教师也要对实验材料进行预设,以便给学生提供及时的帮助,避免数学实验难以为继现象的出现。
二、学生沉浸数学实验实施过程
学生介入数学实验设计过程,为数学实验实施进行了有效的铺垫,潜行“学为中心”还需要引领学生沉浸数学实验实施过程,这是数学实验价值得以实现的关键,也是落实“学为中心”的关键。
1. 深度感知,奠定数学实验之基
目前,数学实验实施存在浅显化现象,缺乏深度效应。这就需要教师基于学生深度感知的需要,全面解放学生,让学生的手、脑、嘴、眼等感官得到有效的激活,引领学生在操作过程中从现象进入本质,发现数学规律。
学生围绕“圆的面积大小跟直徑或半径有关系”的假设,设计了实验“探究圆的面积大小跟直径或半径的关系”。其中一个小组设计了这样的实验:实验材料是几根长度不一的木棒,一瓶墨水;然后用木棒粘上墨水,在一张白纸上围绕圆心进行旋转,得出几个面积不同的圆形;再进行量一量、比一比、折一折等学习活动……学生设计实验能丰富学生实验过程中的认知,让学生借助不同的方法对实验结果获得深度认识。
2. 主动思维,抵达数学实验内核
“学为中心”课堂最显著的一个特性是学生思维发展水平,只有当学生的思维被有效地激活,积极地参与数学实验,主动地去思考,才能使数学实验抵达内核,让学生的思维活性得到有效的提高,独创性思维、批判性思维等得到较好的发展 [3]。
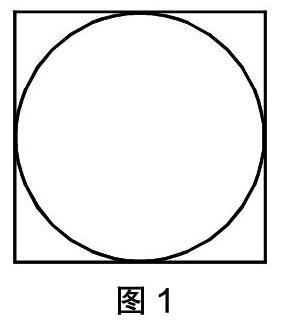
在借助数学实验引导学生认识圆的基本特征的基础上,如何引导学生对圆的特征进行系统性建构是关键,为了激发学生主动性思维,笔者为学生提供了下侧图形材料(图1),让学生根据圆的基本特征,动手操作,找出圆的圆心,量出圆的直径或者半径的长度,并在操作的过程中说出相关的依据,以及实验过程中自己的新发现。
这个环节,通过变式训练的方式,引导学生借助数学实验的方式,找出圆心,量出直径或者半径,充分激发学生思维张力,让学生对所学知识进行整合。最后,鼓励学生借助数学实验寻找新的发现,为学生思维发展开辟新的空间。学生通过实验操作发现,圆和所在正方形边长之间的关系,在圆和正方形之间架设起关联的通道。
3. 交互反思,促进数学实验内化
数学实验实施过程中,为了进一步扩大数学实验效应,离不开学生和学生、学生和教师之间的互动,离不开及时的反思。因此,数学实验实施环节,教师要重视数学实验互动和反思,让学生积极地与同伴、教师进行互动,从而使教师主导作用和学生主体作用得以聚合,让学生间学习成果、思维等得以较好的碰撞、分享。
如上述找圆心、量直径数学实验环节,我们可以为学生提供一个互相展示的机会,并在学生交流的数学实验方案中,选择出一个最佳的方案。反思环节,需要契合数学实验,进行学生进行理性积淀,从所枚举的案例中进行扩展。学生可以根据直径和所在正方形边长之间的关系,快速测量出所在正方形的边长,就可以得出圆的直径或者半径之间的关系。
数学实验是数学课堂的一种常态学习方式,也是潜行“学为中心”课堂的有效方式。然而,数学实验实施效果并不是绝对的,与数学实验设计和实施的“匠心”有关,这就需要教师发挥主导作用,优化数学实验设计和实施的策略,并引导学生对数学实验进行理性反思,让数学实验真正成为潜行“学为中心”课堂的有效方式。
参考文献:
[1] 邱巧均.基于学情 顺学而导——“学为中心”背景下小学数学教学的有效引导策略例谈[J]. 数学教学通讯,2017(13).
[2] 施惠芳. 小学数学实验教学的“数学化”探寻[J]. 江苏教育,2019(09).
[3] 张鹏. 做思相融:数学实验的学习方式[J]. 数学教学通讯,2018(28).
