强化四大意识，实现高效课堂

吴明明

[摘  要] 在高中数学课堂教学中，教师需强化处理教材的意识、能力培养的意识、思想方法的意识以及反思意识，将这些意识融合在教学设计中去，才能更好地聚焦数学知识，引领学生感悟数学本质，促进学生思维的自然生长，实现高效课堂.

[关键词] 高中数学;强化;意识;高效课堂

教师通过有效的教学策略，促进学生的自主学习，实现高效课堂. 近期，笔者提炼总结了四大意识，据此尝试性开展了一系列教学活动，受益颇多. 在践行的过程中，笔者深刻领悟到只有强化这四大意识，并将这些意识融合在教学设计中去，才能更好地聚焦数学知识，引领学生感悟数学本质，促进学生思维的自然生长，实现高效课堂. 下面笔者结合教学实际具体谈一谈.

强化处理教材的意识

是否能创造性地处理好教材是判断一节课优劣的关键所在. 新课改推进下，教育教学专家基于自身的教学经验，对数学教学进行了合理设计与编排，为学生的学习提供了广阔的空间. 只有强化处理教材的意识，创造性地利用好这一重要资源，做教材的开发者和创造者，提供“再加工”更好地指导教师的“教”，服务于学生的“学”，才能充分发挥教材的教育与智力价值，引领学生走进教材感受数学的内涵，感悟数学的真正价值所在.

案例1：以“‘用二分法求方程的近似解”的教学片段为例.

教材例题：使用计算机或计算器用“二分法”求方程2x+3x=7的近似解. （精确度为0.1）

教材中安排了一般性步骤的教学过程，旨在引导学生掌握“‘二分法求方程根的步骤”，为了让学生“知其然，更知其所以然”，笔者作了如下处理：

师：下面，请大家来看如下方程：2x+3x=7. 针对这个方程，你是否可以提出一个数学问题？（学生热情高涨，各个跃跃欲试）

生1：这个方程有几个解？

生2：该方程实数解约是多少？

生3：借助“二分法”是否可求解其近似数？

师：大家提出的问题都非常经典和到位，那我们就一起来一一研究以上问题. 方程2x+3x=7有几个解呢？

生4：我们可以通过作图画出函数y=2x与y=-3x+7的图像，观察图像易发现其仅有一个交点，所以方程2x+3x=7只有一个解.

生5：我的方法与生4不一样. 可以借助工具画出函数2x+3x=7的图像，进一步观察图像与x轴交点的个数，从而得出方程2x+3x=7只有一个解.

……

以上案例中，教师紧密联系教材，却又不拘泥于教材，针对例题精心设计本源性问题，揭示例题的本质，贯穿于例题教学的始终，使其具有数学的生长力，引发学生层层递进的思考和探究，让学生充分经历学习的过程，充分体验探究学习到提炼问题本质的生命历程.

强化能力培养的意识

作为新课改推进下的数学课堂，不仅需引领学生习得相应的数学知识，更需注重学生能力的培养，强化“能力立意”，提升学生的数学素养. 因此，作为一名数学教师，应从学生的具体学情出发，完善学生各方面的能力，以此提升数学课堂教学的效率.

案例2：以“函数奇偶性”的教学片段为例.

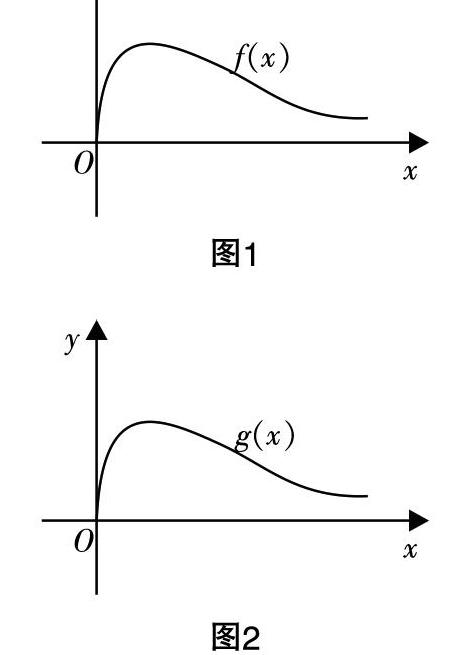
问题呈现：已知f（x）为偶函数，g（x）为奇函数，试将图1和图2补充完整.

分析：函数知识贯穿于整个中学的始终，是学生学习的主线，所以其重要性是毋庸置疑的. 本题对函数奇偶性的考查十分纯正，跳出了此类知识考查的怪圈，主要考查学生的作图能力，十分清新怡人. 图1中的f（x）为偶函数，那么在作图时只需完成已知部分图像关于y轴对称;而图2中的g（x）为奇函数，那么在作图时作出已知部分图像关于原点对称. 为了解决这一难点问题，笔者引导学生思考：如何作出点P（x，y）关于原点的对称点P′？学生经过思考不难得出，先作g（x）的已知图像关于y轴的对称图像g■（x），再作g■（x）关于x轴的对称图像g■（x）即可. 当然，问题解决到这里并没有结束，笔者又做了更进一步的推广和引申：如何作出y=f（x）关于点（a，b）的对称图像？进一步思考，可以得知：先作y=f（x）关于直线x=a的对称图像，再作关于直线y=b的对称图像. 就这样，一步步地帮助学生将“轴对称图形、中心对称图形的作法”收入囊中.

这样，在学习新知和讲评习题的过程中，通过推广和引申这种潜移默化的影响，帮助学生逐步建立起一种理性认识，在这种同化与顺应的内化过程中，获得新的经验，发展数学能力，使核心素养得以生根发芽，茁壮生长.

强化思想方法的意识

思想方法是数学知识、技能和方法的“灵魂”，是促成数学能力与数学意识的“催化剂”. 在高考中，几乎每一道热点问题或把关题都含有多种数学思想. 在解题教学中，需强化思想方法的意识，将数学思想深入到数学的“灵魂深处”，同时让学生勤于总结，时常反思，进而提炼得出理论精髓，最终提升自身的数学学习水平.

案例3：以“三角函数最值”的教学片段为例.

问题呈现：试求出函数y=sinx+cosx+sinx·cosx的最值.

分析：本题是针对这一课题特别补充的，问题的表述简洁明晰，但难度较大. 笔者通过引领学生分析和探索，让学生自主发现sinx+cosx与sinx·cosx间的关系，这就需要进行换元，将此处的三角函数的最值问题转化为二次函数在闭区间上的最值问题，考查学生的化归思想. 不难想到，sinx+cosx与sinx·cosx可相互转化，进而引入代换t=sinx+cosx，t∈[-■，■]，则sinx·cosx=■（t2-1），y=■+t=■（t+1）2-1. 因为t∈[-■，■]，所以-1≤y≤■+■. 当t=■，即x=2kπ+■时，y■=■+■（k为整数）;当t=-1，即x=kπ+■或x=kπ时，y■= -1（k为奇数）.

在多个数学核心素养应运而生的大背景下，再仔细审视以上问题，对新授课教学的导向作用就显而易见了. 我们只有在日常教学中不断强化数学思想意识，才能让学生在知识基础上越站越高，提升数学思维，才能实现高效课堂，进而真正意义上让核心素养在课堂上落地生根.

强化反思意识

反思作為一种积极的心理感知活动，就是个体对自身行为的反省与评价，并能够从中吸取教训，总结经验，实现不断提升的目的. 因此，反思行为的形成，前提条件就是具有反思意识. 教学反思对于教师的教与学生的学有着积极的促进作用，其重要特征就是将“创新教”与“创新学”有效融合，提升教学实践的合理性与有效性. 教学反思是数学教学中最有价值的行为，所以数学教学一定要通过不断反思、不断创新，引导学生善思好问，提升课堂教学效率.

通常在备课时教师都会深入钻研教材，查阅各种资料，精心创设问题情境，试图打造有效互动、气氛活跃、过程流畅的教学过程. 当然，设计这样的教学过程为了就是教会学生更多的知识，启迪学生的数学思维. 但静下心来反思这样的教学过程，真的完美吗？真的是创新的教学方式吗？显然，答案并非肯定的，在这样的教学过程中可以看出，教师的创新教并未从学生的已有认知结构出发，而仅仅是从教学设计的完整性着手去安排学习过程，这样的教学过程显然是与新课程标准不相符的. 此时，教师积极且有效的反思就显得极其生动. 教师只有对自身的教学行为进行不断诊断、不断反思，不断纠正、不断进取、不断创新，才能真正意义上优化自身的教学方式，使得自身的教学行为和教学能力有本质性地提高，进一步实现有效地教，促进学生高效地学，提升课堂教学的质量，达到教学相长、共同发展的目的.

总之，在课堂教学中需强化的四种意识，无论是其中的哪一种，宗旨不外乎一点，就是以教师为主导，学生为主体，创造性的实施教学. 在整个教学中，教师需充分发挥自身的作用，将学生已有经验与数学思维有效地融合在一起，促进学生获得较好的发展，不断提升课堂效率.